EDP Sciences logo
Submit your paper
Search
Menu
All issues Volume 19 / No 3 (2018) Mechanics & Industry, 19 3 (2018) 303 Full HTML
Open Access
Issue
Mechanics & Industry
Volume 19, Number 3, 2018
Article Number 303
Number of page(s) 10
DOI https://doi.org/10.1051/meca/2018008
Published online 05 September 2018

© AFM, EDP Sciences 2018

1 Introduction

Sheet hydroforming process has found popularity due to its profitable advantages such as high product quality, enhanced formability, improved accuracy and economic feasibility in high volume production [1,2]. The advantages are significantly dependent on the applied pressure loading path during the process [3,4]. Development of finite element codes makes the process designers capable of modeling and producing more complicated products with better quality and shorter design time [5–7]. A variety of methods and techniques have been recently developed to improve the robustness of finite element models [8]. Finite element software would be more useful if empowered with optimization algorithms or artificial intelligence systems to provide a powerful tool in analyzing and designing of products.

Several studies have been reported on simulation-based optimization of loading paths in sheet and tube hydroforming processes. Ray and MacDonald [9] determined the optimal loading path for tube hydroforming process using a fuzzy logic control (FLC) algorithm and finite element analysis. Choi et al. [10] developed an adaptive finite element analysis with fuzzy control algorithm to determine the optimal hydraulic pressure and blank holder force simultaneously in warm sheet hydroforming. Li et al. [11] integrated an adaptive finite element approach with an FLC algorithm to optimize the loading paths in tube hydroforming process. Abedrabbo et al. [12] employed genetic algorithm by an optimization software in combination with finite element method to optimize the loading paths in tube hydroforming process. Mirzaali et al. [13,14] incorporated the simulated annealing (SA) algorithm and finite element method to obtain the optimal loading paths for hydroforming of copper tubes. Teng et al. [15] developed an adaptive simulation approach integrated with a fuzzy control algorithm to optimize the loading path in T-shaped tube hydroforming. Seyedkashi et al. [16,17] proposed an adaptive SA algorithm in conjunction with finite element simulations to determine the optimal pressure and feed loading paths in warm tube hydroforming. Teimouri and Ashrafi [18] employed finite element simulation and response surface methodology to find out optimal parameter setting of hydroforming process.

In this research, a new adaptive simulation-based optimization approach is proposed by combination of ANSYS parametric design language (APDL), SA optimization technique and FLC. This method is utilized and validated in optimization of sheet hydroforming process. To obtain the optimal pressure profile, first the SA generates the maximum pressure stochastically, and finds the minimum thinning percentage. Then, FLC regulates the appropriate time needed to reach the maximum pressure pertinent to thinning and pressure variations. Finally, APDL measures the maximum thinning at each iteration considering the wrinkling and necking failures. An intermediate MATLAB code is developed and used to link the data between APDL, SA and FLC automatically without any interference of designer during the optimization process. The new optimization approach as a reliable design tool is developed here to make the process designers and engineers capable of modeling and manufacturing more complex products with higher quality and shorter design time. The experimental results proved that the proposed optimization approach is valid for sheet hydroforming process. It could be also applicable for similar multi-objective processes with large search spaces.

2 Methods and materials

2.1 Experimental

In sheet hydroforming process, there are different methods to pressurize the fluid inside the die chamber [19,20]. In this research, a passive-pressurized hydrodynamic deep drawing (PHDD) was utilized. The die chamber and the blank-holder are slightly modified in order to provide a radial pressure around the blank [21]. Figure 1 shows the modified die set for PHDD process which provides less oil leakage and a higher maximum pressure during the process. An optimized pressure load provides proportionate tensile stresses around the blank and prevents rupture and wrinkling failures during the process.

Experiments were performed on an St14 steel sheet with initial thickness of 1 mm and initial diameter of 120 mm. Material properties of St14 were obtained by standard uniaxial tensile test as follows; strain hardening exponent (n) of 0.34, hardening coefficient (k) of 668.3 MPa, Young’s modulus (E) of 210 GPa, Poisson’s ratio (υ) of 0.3, and density (ρ) of 7850 kg/m3. The dimensional details applied in experimental tests were: die inside diameter = 75 mm, die entrance radius = 4.5 mm, inside diameter of blank-holder = 72.7 mm, entrance radius of blank-holder = 3.5 mm, cylindrical diameter of punch = 72.5 mm, minimum conical diameter = 40 mm, punch tip radius = 8 mm, punch corner radius = 1 mm, and punch angle = 45°.

thumbnail Fig. 1

Experimental set-up for the modified PHDD process.

2.2 ANSYS parametric design language (APDL)

A finite element code was developed to model the PHDD process using APDL to facilitate the modeling of various configurations. Any cup-shaped products can be modeled by this APDL code with definition of material properties and geometrical parameters at the beginning of the optimization process. Since the SA method requires many iterations for optimization, a two-dimensional model with PLANE162 element is considered in APDL code to provide a shorter optimization time. The mesh numbers and sizes are parametrically designed depending on the blank dimensions (round of 4 × Total Thickness in width and 1 × Diameter in length). Figure 2 displays a model of the PHDD process extracted from APDL code. Boundary conditions and allowed degrees of freedom are defined as; (1) full constraints on the die and the blank-holder, (2) vertical downward movement on the punch, and (3) pressure on/around the formable sheet. “Automatic single surface contact” is used to define the contact between the blank/punch, blank/die, and blank/blank-holder with friction coefficients of 0.14, 0.04, and 0.04, respectively [22].

Necking and wrinkling failures can be determined from the APDL outputs using an intermediate script code in MATLAB. Thinning amount is calculated in APDL simulation with measuring the distance between the upper and lower nodes of the sheet. If the measured distance exceeds maximum allowable thinning derived by equation (1), necking would occur [23]. 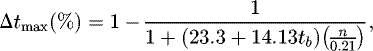(1) where tb is the initial blank thickness and n the strain hardening exponent. On the other hand, wrinkling is checked by calculating the distance between the upper nodes of the sheet and the outer nodes of the punch using equations (2) and (3). If this distance becomes more than 0.1 mm, wrinkles will appear. If any failure (necking or wrinkling) is found after the APDL run, the current variables would be discarded without entering the optimization algorithm, and new variables would be proposed accordingly. 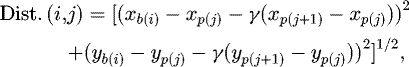(2) 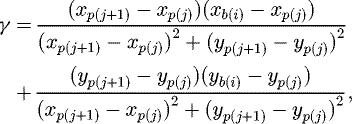(3)where i and j are node numbers of the blank and the punch, respectively; xb and yb coordinates of the blank node; and xp and yp coordinates of the punch node.

An intermediate MATLAB code was developed and used to manage data transfer automatically between APDL simulation and optimization algorithms (Appendix).

thumbnail Fig. 2

PHDD process simulation using APDL.

2.3 Simulated annealing (SA)

During the last decade, SA algorithm was one of the interesting techniques among metaheuristic optimization methods for solving the engineering problems in an iterative manner. The idea of SA was initiated by Metropolis et al. [24] and used by Kirkpatrick et al. [25] for the first time to solve an optimization problem. SA method is inspired from a heat treatment process called “annealing” in which a metal is heated up and then cooled down to a homogenous crystalline structure to reach the thermodynamic equilibrium [26]. SA uses a stochastic search technique to define the minimum energy for a goal function at each temperature. An acceptance rule checks the new energy when generated. If the new energy (Enew) has a goal function value smaller than the previous energy (Eold), the new energy would be accepted. Otherwise, the new energy is accepted only if the value derived by the Boltzmann function  be more than a random number from the range (0,1). T in the Boltzmann function is the system temperature.

In this research, a new adaptive SA algorithm is developed according to the searching trend of the process to provide a set of self-adjusted parameters during the optimization process. It results in increase of the convergence precision, and reduction of the performance time.

Determination of the optimal pressure profile is the main concern in production of desired products in different hydroforming techniques. Definition of the pressure loading profile consists of two important parts; the maximum pressure (Pmax), and the time to reach Pmax. In the proposed method, the maximum pressure is generated using the SA technique, while the time to reach Pmax is simultaneously assigned to a defined FLC algorithm to achieve an optimal pressure profile in a shorter time. Here, the SA algorithm considers the maximum pressure as an input variable, and generates it randomly in each iteration via equation (4): 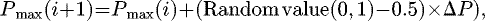(4) where neighborhood radius 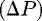–which affects the input variable in each iteration during the optimization process– is calculated by equation (5). 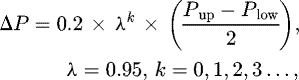(5)where Pup is the upper pressure bound, Plow the lower pressure bound, and k the number of temperature reduction steps. λ must be defined specifically for each SA problem through trial-and-error. In this problem, it is selected as 0.95. Lower and upper pressure bounds [27,28] which are dependent on sheet material properties and geometrical characteristics of the workpiece can be obtained via equations (6) and (7), respectively, 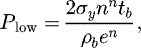(6) 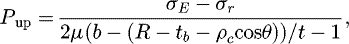(7)where ρb is the blank curvature, σy yielding stress, σE critical axial stress, σr critical radial stress, μ coefficient of friction, b current flange radius, R the largest punch radius, ρc critical blank curvature, and θ is the half cone angle. In case of θ = 0, the cup shape becomes cylindrical, so that it can be analyzed as well as conical cups.

The final goal here is to produce a desired hydroformed cup with minimum thinning and without any defects. Hence, the maximum thinning percentage of the cup is considered as the goal function, which should be minimized. Maximum thinning value is considered as the system energy, and is obtained by calculation of the distance between the upper and lower nodes of the sheet after APDL run in each iteration.

The main framework of cooling schedule in the SA algorithm consists of initial temperature, cooling function, Markov chain number, and final temperature. These parameters have significant effects on convergence precision and performance time. The cooling function is developed using equation (8), which shows a fast cooling trend to expedite convergence ratio. The initial temperature − which is calculated by equation (9) based on the energy changes (ΔE) upon 60% acceptability (Ac) of random variable – affects the Boltzmann and the cooling functions. The final temperature is defined as the system’s convergence condition. Stop condition is satisfied when the energy change is lower than 0.001 or the number of temperature reduction steps becomes more than 20. When the system energy reaches the final temperature, the global optimum would be obtained. 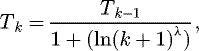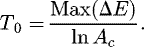(8) (9)

Markov chain is the number of iterations in each temperature which is derived from cooling function in finding the minimum energy. A new function is developed for Markov chain based on the acceptance number (An(k)) and the Boltzmann function in equation (10). (10)

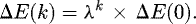As temperature is reduced during the process, the acceptance number and the Boltzmann function are reduced by equations (11) and (12), respectively, (11) (12)

Using equations ((8)–(12)), Markov chain function is expanded as equation (13) and provides a self-adjusted parameter with an ascending-descending behavior during the optimization process. Ascending trend in early iterations increases the acceptance probability, and avoids entrapment in local minima, while descending trend avoids ineffective and excess iterations, and decreases the total run time. 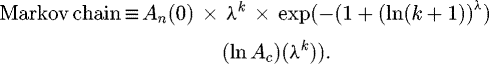(13)

The SA algorithm is developed and performed here by writing a script able to be linked with APDL and FLC algorithm in MATLAB (Appendix).

2.4 Fuzzy logic control (FLC)

Fuzzy theory was initiated by Lotfi A. Zadeh in 1965, and then he proposed the concepts of Fuzzy algorithms in 1968 [29,30]. Fuzzy logic is a flexible computational tool for inserting organized human knowledge into applicable algorithms. Fuzzy logic-based control is used in various applications especially in processes with lack of quantitative data concerning the input–output relations. The fuzzy logic is on the basis of fuzzy set theory in which inputs and output have a degree of membership in a defined set. Over the last decade, FLC algorithm is increasingly utilized in optimization problems in engineering fields.

As mentioned before, here the time to reach the maximum pressure (Pmax) is generated by FLC. The reason to use FLC algorithm was the fact that a multi-objective SA optimization demanded a large number of iterations, and accordingly a long time.

Considering the maximum pressure and the maximum thinning as input variables by FLC, it is possible to regulate the time to reach Pmax during the course of APDL run. Maximum pressure is evaluated using upper pressure bound (Pup), while maximum thinning is evaluated using maximum allowable thinning (Δtmax). These parts are explained in APDL and SA sections. The input variables are fuzzed here into three categories: low (0, Pup/3), medium (Pup/4, Pup/2), and high (Pup/3, Pup) for the maximum pressure; and not-good (NG) (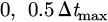), good (G) (0.4 Δtmax, 0.6 Δtmax), and very-good (VG) (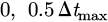) for the maximum thinning percentage. These input variables could be fuzzed into more categories if a more sensitive control was needed. The range of input variables is determined based on the past experience of the process designer. The membership functions pertinent to maximum pressure and maximum thinning generate degrees among 0 – 1. The membership functions for input variables are illustrated in Figures 3a and 3b.

The time to reach Pmax is calculated by determination of an output variable α in FLC algorithm from equation (14), (14) where Δt is the neighborhood radius which is defined as half of a run time of a single FE simulation by APDL code. Similarly, the output variable α is divided here into three categories, i.e. negative, zero, and positive. The membership function of the output variable is shown in Figure 3c.

The knowledge base of the fuzzy system can be categorized into two operative designs; the rule base and the data base. The rule base is employed here using Mamdani type inference which is designed in the form If-Then rules. The degree of output variable is derived according to the Fuzzy rule matrix which is shown in Table 1. Then, the Fuzzy rules must be defined based on the past experience of the process designer. Nine fuzzy rules are defined here according to the input variables as follows:

  • Rule#1: If (Max Pressure is LP) and (Max Thinning is NG) then (α is Negative) Means Rule1 = Min(LP, NG).

  • Rule#2: If (Max Pressure is LP) and (Max Thinning is G) then (α is Negative) Means Rule2 = Min(LP, G).

  • Rule#3: If (Max Pressure is LP) and (Max Thinning is VG) then (α is Negative) Means Rule3 = Min(LP, VG).

  • Rule#4: If (Max Pressure is MP) and (Max Thinning is NG) then (α is Positive) Means Rule4 = Min(MP, NG).

  • Rule#5: If (Max Pressure is MP) and (Max Thinning is G) then (α is Zero) Means Rule5 = Min(MP, G).

  • Rule#6: If (Max Pressure is MP) and (Max Thinning is VG) then (α is Negative) Means Rule6 = Min(MP, VG).

  • Rule#7: If (Max Pressure is HP) and (Max Thinning is NG) then (α is Positive) Means Rule7 = Min(HP, NG).

  • Rule#8: If (Max Pressure is HP) and (Max Thinning is G) then (α is Positive) Means Rule8 = Min(HP, G).

  • Rule#9: If (Max Pressure is HP) and (Max Thinning is VG) then (α is Zero) Means Rule9 = Min(HP, VG).

For example, if Pmax is low (LP), the time to reach Pmax should be decreased regardless of the maximum thinning. If Pmax is medium (MP) while the maximum thinning is not-good (NG), the time to reach Pmax would be increased. If the maximum pressure is high (HP) and maximum thinning is very-good (VG), it is no need to change the time to reach Pmax.

Using Fuzzy centroid of the area in equation (15), the output α determines whether the time to reach Pmax would be changed or not. 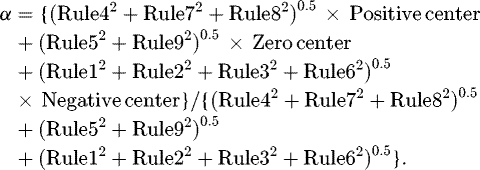(15)

The FLC algorithm is developed and performed here using a script in MATLAB to be linked with APDL and SA algorithm (Appendix).

thumbnail Fig. 3

Membership functions of FLC algorithm for (a) maximum pressure, (b) maximum thinning, and (c) output.
Table 1

Fuzzy logic rules for loading profile control.

3 Results and discussions

In this research, to obtain the optimal pressure loading profile in a shorter time with higher precision, an SA algorithm integrated with APDL code and FLC algorithm is adaptively developed. Both SA and FLC algorithms are executed using developed scripts in MATLAB program in order to take the material properties and geometrical characteristics of the product, to link with the simulation code (APDL), to calculate the upper and lower pressure bounds and maximum allowable thinning, to check the nodes distance for wrinkling and necking measurement, to generate the new pressure loading profile in each iteration, acceptance rule, Fuzzy rules, and convergence condition, and finally store and analyze the optimization outputs to reach the global optimum automatically without any interference of designer during the process execution.

Interaction between APDL, SA and FLC is depicted by a flowchart in Figure 4. At the beginning of the optimization process, it is possible to define the FE model configurations with material properties and dimensions of a conical-cylindrical cup. The maximum thinning of the hydroformed product should be checked after APDL run to check the quality. Also, occurrence of wrinkling or necking should also be checked after each simulation to make sure that the formed cup conforms to the shape of the punch. Then, the APDL output is analyzed by the SA code to discover which loading profile belongs to the minimum obtained thinning. In each iteration, FLC algorithm regulates the loading profile to expedite the total run time. This loop is iterated several times up to the Markov chain number until the final temperature is achieved, and global optimum is obtained.

To investigate the reliability and superiority of the proposed optimization approach over other similar methods, both non-adaptive and adaptive SA approaches [17] are compared with Fuzzy SA approach in Table 2. In the adaptive definition, the algorithm parameters are defined according to the algorithm results, while in the non-adaptive definition all parameters are defined independent of the algorithm results. The less acceptable iterations, the faster convergence ratio can be obtained via the proposed Fuzzy SA method. Also, more precise results are obtained with less thinning and less error. The obtained error is calculated relative to the thinning difference between the simulated model and the experiments. As it is seen, the adaptive SA can provide faster convergence ratio and more precise results than non-adaptive one, but using the FLC algorithm along with the adaptive SA has highly affected the convergence trend and the number of acceptable iterations. Fewer iterations and less error are obtained using the self-adjusted parameters comprising the variable Markov chain number, ascending–descending behavior of cooling function, and proper initial and final temperature in SA algorithm. For better realization, the data convergence trend to reach the goal function is displayed in Figure 5 for a hydroformed cup using the adaptive Fuzzy SA, adaptive SA and non-adaptive SA optimization techniques. It can be inferred from Figure 5, that convergence condition is satisfied after 127 acceptable iterations of APDL run for Fuzzy SA, 202 acceptable iterations for adaptive SA and 241 acceptable iterations for non-adaptive SA. Goal function is converged to 12.3293, 12.9778 and 13.0491, respectively. Consequently, Fuzzy SA approach reduces excessive iterations in FE simulations significantly, and increases the convergence precision in optimization of hydroforming process.

Each minimum goal function is dependent on a specific set of input variables. As mentioned previously, input variable is defined as a loading profile which comprises of the maximum pressure and the time needed to reach it. The optimized loading profile–obtained by the Fuzzy SA approach–is shown in Figure 6. The simulated model and the relevant experiment under the obtained loading profile are also shown.

In Figure 7, thickness distributions at marked points in experimental and simulated products under the optimal pressure loading profile are compared in order to validate the FE and optimization outputs. As it is seen, the maximum thinning occurs at the tip radius of workpiece. The error of the optimization method on this area is calculated based on equation (16). 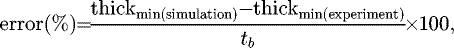(16) where thickmin(simulation) is the minimum thickness of the simulated model, thickmin(experiment) the minimum thickness of the experimental cup, and tb is the initial blank thickness. The error obtained by equation (16) for related conical-shaped cup is 0.2293 as mentioned in Table 2 for Fuzzy SA method.

Maximum deviation between the real and simulated workpiece under the optimal loading profile is approximately 3.14% which demonstrates the reliability of the proposed optimization approach.

thumbnail Fig. 4

Interconnection between adaptive APDL, SA and FLC.
Table 2

Fuzzy SA approach compared with adaptive and non-adaptive SA approaches.

thumbnail Fig. 5

Comparison of data convergence trend in different optimization approaches.
thumbnail Fig. 6

Optimized pressure loading profile corresponding to relative simulation and experiment.
thumbnail Fig. 7

Thickness distribution under the optimal loading profile (thickness in mm).

4 Conclusions

In this research, a new adaptive optimization approach is developed to determine the optimal pressure loading profile for hydroforming of cup-shaped products using combination of APDL, SA algorithm, and FLC. The following results could be concluded in this research: 

  • (1)

    A general and flexible script code is developed to take the material properties and geometrical dimensions parametrically at the beginning of the optimization process, and to create an industrial tool for optimizing of hydroforming process of any symmetric shell cups;

  • (2)

    Finite element simulation using APDL code with parametric definition of process parameters creates flexibility on the proposed approach in which any symmetric cup-shaped products can be modeled;

  • (3)

    Adaptive definition of SA parameters results in reduction of iterations, and increasing of convergence ratio and performance speed, and accordingly provides designer more precise results for hydroforming process;

  • (4)

    regulation of the pressure loading profile using FLC along with SA technique resulted in fewer iterations of APDL run, higher convergence precision and better quality of the final product;

  • (5)

    the proposed approach is elevated using necking and wrinkling definitions to detect imperfect products during the optimization process and avoid improper variables from taking part into the optimization loop.

Nomenclature

An(k): Acceptance number

Dist.: Distance of sheet node from corresponding punch node

E: Energy (max. thinning amount)

Enew: New energy

Eold: Previous energy

Emin: min. energy

Emax: max. energy

Tk: Cooling temperature

△E: Energy changes

Pmax: max. pressure

Emin: Initial pressure

△P: SA neighborhood radius

Pup: Upper pressure

Plow: Lower pressure

Pnew: New pressure

Pold: Previous pressure

Popt: Optimum pressure

T0: Initial temperature

α: FLC output variable

LP: Low pressure

MP: Medium pressure

HP: High pressure

NG: not-good

VG: very-good

Rand: Random number

tnew: New time to reach maximum pressure

told: Previous time to reach maximum pressure

tmin: min. time to reach maximum pressure

tmax: max. time to reach maximum pressure

topt: Optimum time to reach maximum pressure

i: Total loop number

m: Internal loop number

k: External loop number

△tmax: Maximum allowable thinning

△t: FLC neighborhood radius

MC: Markov chain

Appendix

The pseudo code of APDL-FLC-SA optimization approach for sheet hydroforming process:

1. Input material properties and geometrical parameters of workpiece

2. Read T0⁡, P0⁡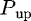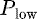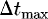, , , (Eqs. (1), (6), (7), and (9))

3. Run APDL simulation to generate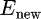

4. Set i by 0, k by 0, m by 0

5. Set LP by 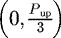, MP by 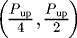, HP by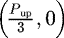 

6. Set NG by (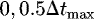), G by (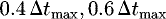), VG by ()

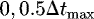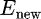7. Set by , Emax by −1

8. WHILE m < MC (Eq. (13))

9. Set i by i + 1

10. Check Fuzzy Rules (Table 1): IF AND

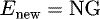
THEN Set Rule1 by Min(LP, NG)

ELSE IF 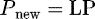AND

THEN Set Rule2 by Min(LP, G)

ELSE IF 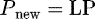 AND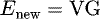

THEN Set Rule3 by Min(LP, VG)

ELSE IF 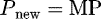 AND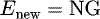

THEN Set Rule4 by Min(MP, NG)

ELSE IF  AND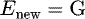

THEN Set Rule5 by Min(MP, G)

ELSE IF 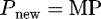 AND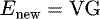

THEN Set Rule6 by Min(MP, VG)

ELSE IF 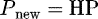  AND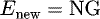

THEN Set Rule7 by Min(HP, NG)

ELSE IF 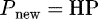AND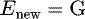

THEN Set Rule8 by Min(HP, G)

ELSE IF 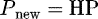 AND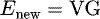 

THEN Set Rule9 by Min(HP,VG)

11. END IF

12. Generate α (Eq. (15))

13. Generate tnew (Eq. (14))

14. Generate 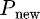 (Eq. (4))

15. Run APDL simulation to generate  and

16. IF  >  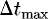and 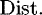 > 1 mm

THEN go to line 9

17. END IF

18. Check SA acceptance rule: IF 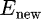 <  OR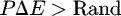

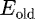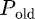THEN Set by , 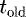by, by 

ELSE go to line 9

19. END IF

20. Set m by m + 1

21. IF  <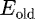 

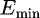
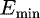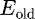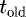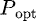THEN Set by , by , 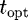by, by 

ELSE IF 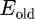 > Emax

THEN Set by  Emax by 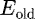,  tmax by 

22. END IF

23. END WHILE

24. Set m by 0, and k by k + 1

25. Calculate 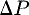, , and Tk (Eqs. (5) and (8))

26. IF 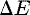 > 0.001 OR k < 20

THEN go to line 7

27. END IF

28. END

References

  1. Y.Z. Chen, W. Liu, S.J. Yuan, Strength and formability improvement of Al-Cu-Mn aluminum alloy complex parts by thermomechanical treatment with sheet hydroforming, J. Miner. Met. Mater. Soc. 67 (2015) 938–947 [CrossRef] [Google Scholar]
  2. Y.Z. Chen, W. Liu, Y.C. Xu, S.J. Yuan, Analysis and experiment on wrinkling suppression for hydroforming of curved surface shell, Int. J. Mech. Sci. 104 (2015) 112–125 [CrossRef] [Google Scholar]
  3. A. Hashemi, M. Hoseinpour-Gollo, S.M.H. Seyedkashi, Process window diagram of conical cups in hydrodynamic deep drawing assisted by radial pressure, Trans. Nonferrous Met. Soc. China 25 (2015) 3064–3071 [CrossRef] [Google Scholar]
  4. M. Mashhadi, A. Hashemi, M. Bakhshi-Jooybari, A. Gorji, Effect of punch profile on thickness distribution in hydromechanical deep drawing of conical-cylindrical parts, Adv. Mater. Res. 445 (2012) 143–148 [CrossRef] [Google Scholar]
  5. R. Bihamta, Q.H. Bui, M. Guillot, G. D’Amours, A. Rahem, M. Fafard, Global optimisation of the production of complex aluminium tubes by the hydroforming process, CIRP J. Manuf. Sci. Technol. 9 (2015) 1–11 [CrossRef] [Google Scholar]
  6. M. Imaninejad, G. Subhash, A. Loukus, Loading path optimization of tube hydroforming process, Int. J. Mach. Tools Manuf. 45 (2005) 1504–1514 [CrossRef] [Google Scholar]
  7. A. Afshar, R. Hashemi, R. Madoliat, D. Rahmatabadi, B. Hadiyan, Numerical and experimental study of bursting prediction in tube hydroforming of Al 7020-T6, Mech. Ind. 18 (2017) 411 [CrossRef] [Google Scholar]
  8. S. Daouk, F. Louf, O. Dorival, L. Champaney, S. Audebert, Uncertainties in structural dynamics: overview and comparative analysis of methods, Mech. Ind. 16 (2015) 404 [CrossRef] [Google Scholar]
  9. P Ray, B.J. MacDonald, Determination of the optimal load path for tube hydroforming processes using a fuzzy load control algorithm and finite element analysis, Finite Elem. Anal. Des. 41 (2004) 173–192 [Google Scholar]
  10. H. Choi, M. Koc, J. Ni, Determination of optimal loading profiles in warm hydroforming of lightweight materials, J Mater. Process. Technol. 190 (2007) 230–242 [CrossRef] [Google Scholar]
  11. S. Li, B. Yang, W. Zhang, Z. Lin, Loading path prediction for tube hydroforming process using a fuzzy control strategy, Mater. Des. 29 (2008) 1110–1116 [CrossRef] [Google Scholar]
  12. N. Abedrabbo, M. Worswick, R. Mayer, I.V. Riemsdijk, Optimization methods for the tube hydroforming process applied to advanced high-strength steels with experimental verification, J. Mater. Process. Technol. 209 (2009) 110–123 [CrossRef] [Google Scholar]
  13. M. Mirzaali, G.H. Liaghat, H. Moslemi-Naeini, S.M.H. Seyedkashi, K. Shojaee, Optimization of tube hydroforming process using simulated annealing algorithm, Proc. Eng. 10 (2011) 3012–3019 [CrossRef] [Google Scholar]
  14. M. Mirzaali, S.M.H. Seyedkashi, G.H. Liaghat, H. Moslemi-Naeini, K. Shojaee, Y.H. Moon, Application of simulated annealing method to pressure and force loading optimization in tube hydroforming process, Int. J. Mech. Sci. 55 (2012) 78–84 [CrossRef] [Google Scholar]
  15. B. Teng, K. Li, S. Yuan, Optimization of loading path in hydroforming T shape using fuzzy control algorithm, Int. J. Adv. Manuf. Technol. 69 (2013) 1079–1086 [CrossRef] [Google Scholar]
  16. S.M.H. Seyedkashi, H. Moslemi-Naeini, G.H. Liaghat, M. Mosavi-Mashadi, K. Shojaee-Ghandashtani, M. Mirzaali, Y.H. Moon, Experimental and numerical investigation of simulated annealing technique in optimization of warm tube hydroforming, Proc. Inst. Mech. Eng., Part B: J. Eng. Manuf. 226 (2012) 1869–179 [CrossRef] [Google Scholar]
  17. S.M.H. Seyedkashi, H. Moslemi-Naeini, Y.H. Moon, Feasibility study on optimized process conditions in warm tube hydroforming, J. Mech. Sci. Technol. 28 (2014) 2845–2852 [CrossRef] [Google Scholar]
  18. R. Teimouri, H. Ashrafi, Optimization of hydroforming process for deep drawing of AA7075 using finite element simulation and response surface methodology, Trans. Indian Inst. Met. 70 (2017) 2265–2275 [CrossRef] [Google Scholar]
  19. B. Meng, M. Wan, X. Wu, S. Yuan, X. Xu, J. Liu, Development of sheet metal active-pressurized hydrodynamic deep drawing system and its applications, Int. J. Mech. Sci. 79 (2014) 143–151 [CrossRef] [Google Scholar]
  20. A. Hashemi, M. Mashhadi, M. Bakhshi-Jooybari, A. Gorji, Study of the effect of material properties and sheet thickness on formability of conical parts in hydro-mechanical deep drawing assisted by radial pressure, Adv. Mater. Res. 445 (2012) 149–154 [CrossRef] [Google Scholar]
  21. A. Hashemi, M. Hoseinpour-Gollo, S.M.H. Seyedkashi, Bimetal cup hydroforming of Al/St and Cu/St composites: adaptive finite element analysis and experimental study, J. Mech. Sci. Technol. 30 (2016) 2217–2224 [CrossRef] [Google Scholar]
  22. X. Liu, Y. Xu, S. Yuan, Effects of loading paths on hydrodynamic deep drawing with independent radial hydraulic pressure of aluminum alloy based on numerical simulation, J. Mech. Sci. Technol. 24 (2008) 395–399 [Google Scholar]
  23. A. Hashemi, M. Hoseinpour-Gollo, S.M.H. Seyedkashi, Study of Al/St laminated sheet and constituent layers in radial pressure assisted hydrodynamic deep drawing, Mater. Manuf. Process. 32 (2017) 54–61 [CrossRef] [Google Scholar]
  24. N. Metropolis, A. Rosenbluth, M. Rosenbluth, A. Teller, E. Teller, Equation of state calculations by fast computing machines, J. Chem. Phys. 21 (1953) 1087–1092 [NASA ADS] [CrossRef] [Google Scholar]
  25. S. Kirkpatrick, C.D. Gelatt, M.P. Vecchi, Optimization by simulated annealing, Science 220 (1983) 671–680 [NASA ADS] [CrossRef] [MathSciNet] [PubMed] [Google Scholar]
  26. S.M.H. Seyedkashi, H. Moslemi-Naeini, G.H. Liaghat, M. Mosavi-Mashhadi, M. Mirzaali, K. Shojaee, Y.H. Moon, The effect of tube dimensions on optimized pressure and force loading paths in tube hydroforming process, J. Mech. Sci. Technol. 26 (2012) 1817–1822 [CrossRef] [Google Scholar]
  27. A. Fazli, B.M. Dariani, Theoretical and experimental analysis of the axisymmetric hydromechanical deep drawing process, Proc. Inst. Mech. Eng., Part B: J. Eng. Manuf. 220 (2006) 1429–1437 [CrossRef] [Google Scholar]
  28. A. Jalil, M. Hoseinpour-Gollo, S.M.H. Seyedkashi, Process analysis of hydrodynamic deep drawing of cone cups assisted by radial pressure, Proc. Inst. Mech. Eng., Part B: J. Eng. Manuf. 231 (2017) 1793–1802 [CrossRef] [Google Scholar]
  29. L.A. Zadeh, Fuzzy sets, Inf. Control 8 (1965) 338–353 [Google Scholar]
  30. L.A. Zadeh, Fuzzy algorithms, Inf. Control 12 (1968) 94–102 [CrossRef] [Google Scholar]

Cite this article as: A. Hashemi, M.H. Gollo, S.M.H. Seyedkashi, Application of a new integrated optimization approach in sheet hydroforming process, Mechanics & Industry 19, 303 (2018)

All Tables

Table 1

Fuzzy logic rules for loading profile control.

In the text
Table 2

Fuzzy SA approach compared with adaptive and non-adaptive SA approaches.

In the text

All Figures

thumbnail Fig. 1

Experimental set-up for the modified PHDD process.
In the text
thumbnail Fig. 2

PHDD process simulation using APDL.
In the text
thumbnail Fig. 3

Membership functions of FLC algorithm for (a) maximum pressure, (b) maximum thinning, and (c) output.
In the text
thumbnail Fig. 4

Interconnection between adaptive APDL, SA and FLC.
In the text
thumbnail Fig. 5

Comparison of data convergence trend in different optimization approaches.
In the text
thumbnail Fig. 6

Optimized pressure loading profile corresponding to relative simulation and experiment.
In the text
thumbnail Fig. 7

Thickness distribution under the optimal loading profile (thickness in mm).
In the text

Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.

Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.

Initial download of the metrics may take a while.