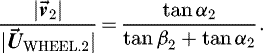| Issue |
Mechanics & Industry
Volume 20, Number 1, 2019
|
|
|---|---|---|
| Article Number | 107 | |
| Number of page(s) | 18 | |
| DOI | https://doi.org/10.1051/meca/2019004 | |
| Published online | 04 April 2019 | |
Regular Article
A one-dimensional stage un-stacking approach to reveal flow angles and speeds in a multistage axial compressor at the design operating point
1
School of Mechanical and Aerospace Engineering, Nanyang Technological University (NTU), 50 Nanyang Ave, 639798 Singapore, Singapore
2
Lloyd's Register Global Technology Centre, 1 Fusionopolis Place, #09-11 Galaxis, 138522 Singapore, Singapore
* e-mail: mykng@ntu.edu.sg
Received:
30
April
2018
Accepted:
23
January
2019
Stage stacking methods commonly use a one-dimensional (1D) through flow analysis at the mean line to design individual axial compressor stages and stack these to form a multistage axial compressor. This phase of design exerts a great influence on each stage's pressure and temperature ratio. The design process for an individual stage is usually guided by design values and rules developed in previous designs. This study develops a 1D stage un-stacking method (SUSM), which uses a minimal set of data from an actual axial compressor, while reducing the needed number of assumptions. Proceeding from the premise that an actual axial compressor design fulfills all thermodynamic requirements, velocity triangle requirements and design guidelines simultaneously, this proposed SUSM calculates the pressure, temperature, velocities and flow angles as a set of dependent data at each stage of the axial compressor. In approximating a possible axial compressor design for the LM2500 gas turbine that achieves the known pressure ratio distribution, the suggested stage loading coefficient (SLC) distribution is more appropriately considered an initial well-informed estimate and further improvements to this SUSM are needed to infer the actual SLC distributions used.
Key words: Multistage axial compressor / stage un-stacking approach / velocity triangle / flow design / aero-derivative gas turbine
© AFM, EDP Sciences 2019
1 Introduction
The need for greater efficiency drives each new gas turbine model towards higher overall pressure ratios and power outputs, inevitably keeping the gas turbine relevant. The design ideas implemented in actual gas turbines are complex and delicately optimized across various technological aspects to achieve performance, reliability and cost-effective maintenance. The compressor is often the axial flow design, to pass higher mass flow rates through a relatively smaller frontal area and achieve generally higher stage pressure ratios with lower losses compared to the centrifugal design. With each successive design delivering higher overall pressure ratios, the relevance of the multistage axial flow compressor is not diminishing.
The design process for an axial compressor from simple to challenging are: one-dimensional (1D) analysis at the mean line, two-dimensional (2D) cascade analysis (where the blade rows are unwrapped from the rotational axis), 2D streamline curvature, 1D analysis of radial variation across the blade span resulting in span-wise blade twist angles and three-dimensional (3D) analysis to simulate the challenging actual turbulent flows at the blade root and tip (which contribute heavily to losses). Despite its relative simplicity, the 1D analysis at the mean line exerts great influence on the design of an axial compressor because, at this design phase, each stage's pressure and temperature are defined before detailed design work begins and assembled together.
In 1D analysis through the turbomachine, while the corrected mass flow rate is examined for the effects of pressure, Cumpsty [1] demonstrated that obtaining correct stage stacking or matching will be challenging, because the mass flow rate, effective flow area and pressure are in an intricate relationship. This stage matching challenge is further compounded after incorporating inter-disciplinary aspects into the design space. The gas turbine developed traditionally along distinct components lines and has been tremendously refined to achieve component efficiencies over 90%. The design space is now arguably more complex owing to more disciplines, including inter-disciplinary work. Ghisu et al. [2,3] have developed an integrated design approach using a 1D mean line solver embedded in an optimisation routine, to defer fixing the components interface design parameters till later phases in the design process, resulting in better explorations of the design space and hence harnessing the gains from trade-offs between different components and disciplines. From the observations of Jarrett and Ghisu [4], the search for an optimised balance between time spent on configuration selection and refining a selected configuration during the design process reveals that in the best designs, configuration selection with 1D mean line solvers consumes half to three-quarters of the design time.
The stage stacking process is the core of 1D analysis at the mean line. The stage stacking approaches recorded in the literature focus on building up a compressor stage by stage, with stage temperature and pressure (or equivalent information) available. For the gas turbine manufacturers, the design process may be guided by design values and rules developed in previous compressor designs. Sehra et al. [5] apply existing knowledge and design techniques from an aviation gas turbine to design the compressor of a utility gas turbine. Smed et al. [6] report evolving the design of compressor within a family of gas turbine models. Smith [7] begins unifying compressor models into families based on similar design rules. Mattingly [8] shows that the design process is often iterative as a multitude of performance requirements must be fulfilled simultaneously. In the light of this, the stage flow angles, flow speeds, stage characteristics, among other variables are then the inputs to the stage stacking method. The ability of the blades to maintain un-separated flow at reduced or excessive mass flow rate within a range of off-design flow angles is often summarized as a model, which is usually empirical, derived from experimental data or from performance data of a previous related design.
When tasked to determine the stage details of a multi-stage axial compressor designed by others, the current methods require a large number of inputs, which unfortunately are not known with certainty. While estimates and design guides may be helpful sources of input design variables, there are few systematic ways to un-stack a multi-stage axial compressor, other than iteratively testing with a range of input values for each design variable. The available information on an axial compressor is usually the overall pressure ratios and the overall efficiency, but do not mention how flow angles and flow speeds relate within the machine. The aim of this paper is thus to present a stage un-stacking method (SUSM) that uses minimum information, and applies a feasible relationship between adjacent stages temperature ratio and pressure ratio to infer the flow angles and flow speeds at each stage for the axial compressor operating at the design point.
Presently, this method is restricted to operating conditions at a compressor's design point only. While 2D streamlines curvature methods are the common approach to define the blade geometry and flow angles at each axial stage in relation to the next axial stage, this paper details a 1D approach that trades off calculating for realistic flow physics at blade surfaces for quicker calculation of the mean flow variables.
This paper is divided into the following Sections. The literature is reviewed in Section 1.1. In Section 2, the SUSM is described. The results of stage un-stacking and testing on an approximated 3D model are presented in Section 3. Section 4 discusses the results and is followed by conclusions.
1.1 Literature
The literature contains a number of 1D stage stacking methods for designing an axial compressor from individual stages and stage stacking these together to form a multistage axial compressor.
1.1.1 RSRR approach
The repeating-stage repeating-row (RSRR) model from Mattingly [8], also introduced in an aircraft engine design book by Mattingly et al. [9], is one of the simplest design approach and therefore provides a suitable initial design. However, the constant mean line in this model often does not match that in actual compressors and actual compressor stages are often not repeating as seen in the clearly varying stage axial velocity.
1.1.2 STGSTK code
The STGSTK code by Steinke [10] is an early code used to predict the off-design performance of an axial compressor-based performance at the design operating point. The analysis is performed at the mean-line with velocity triangles at the rotor inlets and outlets. The compressor is built up cumulatively through stage stacking to obtain the multistage design and overall performance. However, the few critical parameters that build the compressor stage by stage are required inputs to STGSTK; therefore, the STGSTK code is unable to provide guidance on the stage-to-stage variation of these critical parameters.
1.1.3 LUAX-C code
A more recent 1D steady state operation stage stacking model is the LUAX-C by Falck [11]. This model is under active development again in 2013 by Perrotti [12]. This model is much more flexible than the RSRR model and has the potential to obtain most of the geometric, thermodynamic and flow conditions in each blade row of each stage. A number of experimentally based enhancements are incorporated, such as empirical relations for incidence angles and deviation angles at each blade row, blade profile losses and endwall losses. However, this model is not used as it required stage solidity and stage reaction as inputs. Another required input which discouraged use is the inflexible distribution of stage loading.
1.2 Deliberately working with limited data
Stage stacking methods that use more inputs generate more feasible designs and are capable of more realistic performance predictions. This is not a challenge for the knowledgeable original equipment designer. However, the reminder of the non-designers looking to analyse the axial compressors and have no intimate access to one, the available information tends to be sparse. A few pieces of necessary information for the studied axial compressor are taken from Pedersen [13]:
-
PWSD load on power turbine (kW);
-
PS2 static pressure at the compressor outlet (Pa);
-
T2 stagnation temperature at the compressor outlet (K);
-
W2 mass flow rate (kg s−1);
-
NGG shaft rotational speed (RPM).
1.3 Supporting information
To supplement the insufficient information gathered in Section 1.2, further inputs for stage un-stacking an axial compressor are sought from only publicly available and conveniently accessible information. For example, approximate radius and axial station coordinates are derived using the following coarse estimation approach to reduce reliance on detailed data. The radius of the casing and hub and axial stations are estimated from a compressor schematic on the gas turbine manufacturer's marketing datasheet [14]. No further inputs are sought from either the original equipment manufacturer or equipment owners, so that the proposed method is also applicable for preliminary analysis of other designs and by students without access to extensive libraries. For the axial compressor examined here, there is much more information available from Klapproth et al. [15] and Wadia et al. [16]. To develop a robust method capable of estimating a compressor's mean line performance close to the actual, information in Klapproth et al. [15] and Wadia et al. [16] are not used to develop the SUSM but only in validating its effectiveness.
2 Methods
Stage stacking assembles individual stages at the design operating point, where the incidence angle at the blade leading edge is small, the flow of the working fluid follows the curvature of the blade and the velocity triangles at the stage outlets are very similar to the velocity triangles at the following inlets.
2.1 Overview of the stage un-stacking method
The SUSM is developed in three main parts and works according to the flowchart of Figure 1. Since an actual gas turbine fulfills simultaneous requirements, iterative calculations are used to match the flow quantities throughout the gas turbine. For parts 1–3 of the model, after the inlet guide vanes (IGV) outlet and outlet guide vanes (OGV) inlet angles are selected as iteration variables, the remaining uncertain design variables are allowed to vary within acceptable bounds. The two largest unknowns are found in the axial variation model (part 2): the axial stage loading coefficient (SLC) and the static pressure ratio distribution. The axial variation of these and other design variables defined within the axial variation model are presented next.
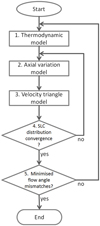 |
Fig. 1 Overview of the stage un-stacking method. Part 1. Thermodynamic model: Sections 2.10.1 and 2.10.2. Part 2. Axial variation model: Sections 2.2 and 2.10.3; Sections 2.3 and 2.10.4; Section 2.4; Sections 2.5 and 2.10.5. Part 3. Velocity triangle model: Sections 2.6 and 2.10.6. |
2.2 Stage loading coefficient (SLC) design rule
Between the compressor inlet and outlet, the SLC indicates the amount of energy imparted to the flow through the specific stagnation enthalpy rise at each stage. Since specific stagnation enthalpy is known only at the compressor inlet and outlet, an SLC model is needed to suggest a feasible axial distribution of SLC at the compressor's design operating point. The maximum feasible specific static enthalpy rise in a stage Δh may be approximated by equation (29) in Bullock and Prasse [17], with subscripts included for clarity.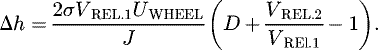 (1)
(1)
The diffusion factor D is defined by equation (13) in Lieblein et al. [18].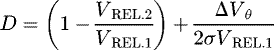 (2)where
(2)where 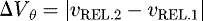 and
and  .
.
In early compressors, Bullock and Prasse [17] reported that the compressor was also designed for reduced outlet axial velocity so that excessive or abrupt deceleration before the combustor was avoided. This meant that the rear stages must use reduced axial velocities and would see smaller specific static enthalpy rises than the front stages. In recent combustor designs, the diffuser design incorporated after the combustor inlet has improved greatly, incurring acceptable stagnation pressure losses while slowing down the flow. This has removed the need for the compressor to produce greatly reduced axial speed for the combustor which Mattingly et al. [19] demonstrated in the design approach for the combustor.
The RSRR compressor design approach in Mattingly [8] treats the diffusion factor D as a design variable. This gives the designer greater flexibility to distribute SLC more evenly throughout the compressor and one feasible axial distribution of SLC is defining the specific stagnation enthalpy rise as a fixed proportion of 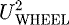 , resulting in constant SLC.
, resulting in constant SLC.
The overall design of the engine is optimised for cost and weight saving. The compressor is of no exception and therefore is likely close to the optimum least weight when finalized, as Smith [7] points out. From his wealth of design experience, Smith [7] emphasizes the importance of loading each stage appropriately through advising designers and designs to work with proven loading criteria achievable through practical mechanical clearances.
When operating at a compressor's design point, this study uses an equal or near equal distribution of SLC, with the following arguments.
-
An axial compressor may improve its overall pressure ratio by adding more stages. Each added stage increases weight and machine complexity such that the design must extract maximum useful output from any stage. Consequently, each stage is then designed applying the same utmost improvements in aerodynamic insight.
-
An axial compressor may also increase its pressure ratio through increasing the individual stage pressure ratio via improved aerodynamic insight and design of the blade rows. Since constraints on weight and machine complexity demand the least number of stages, each stage receives the same improved aerodynamic insight.
-
When no information is available, weight and machine complexity constraints do indicate that each stage shares the compression burden. IGV and OGV stages add and remove swirl respectively and must be presented so the inlet stage and the outlet stage of the compressor are able to impart the same amount of work on the working fluid as the other stages as explained in Mattingly [8].
2.3 Pressure ratio design rule
While a compressor is designed to be highly efficient, there will be losses and specific entropy rise across each stage, stemming from irreversibility in compression. Considering the need to minimize weight and complexity again, the relationship between the stage pressure ratios would be similar to that for SLC; each stage bears a similar burden. A feasible axial distribution of pressure ratios when operating at a compressor's design point is a near-equal distribution, dividing the overall pressure ratio into near-equal stage pressure ratios or near-equal diffusion processes for all stages.
Based on the compressor's pressure rise and temperature rise, a corresponding overall specific entropy rise is already incurred. After apportioning the compressor pressure rise and temperature rise nearly equally across all stages, each stage is able to see a small but unavoidable specific entropy rise.
2.4 Axial velocity design rule
For minimal buildup of wakes and boundary layers to maximise effective flow area for greater mass flow rates, Bullock and Prasse [17] point out the need to minimise abrupt changes at the mating surfaces of the stage inlets and outlets. Implementing this guide, the casing and hub walls are constructed to vary smoothly from compressor inlet to outlet so that changes to the boundary layers and then wakes are gradual. The axial velocity distribution model takes in the resulting smoothly varying cross-section areas and also requires that the axial temperature and axial pressure distributions return a density distribution that is varying smoothly. This results in a smooth variation of axial velocity for use in further analysis with velocity triangles.
2.5 Axial blockage design rule
Due to boundary layers and wakes accumulating from stage to stage, the effective flow area at each stage gradually decreases. While the blockage in the compressor increases, the ideal distribution must be smoothly changing so that the available flow area is able to give a smooth axial velocity profile. This works in tandem with Smith's [7] advice of removing all forward facing steps and obtaining surface finishes to appropriate smoothness. This study includes the effect of viscosity as an additional increase in blockage over mechanical blockage from the rotor and stator blades.
2.6 Velocity triangles design rule
The velocity triangle rule is implemented in part 3 of the SUSM. At the design operating point, a compressor is performing at its ideal state aerodynamically, based on the advice of Smith [7] that the blades are uniquely designed for the design operating point. The working fluid follows the curvature of the blades with minimum deviations from the design intention. For minimum variation in flow angles between the exit plane of a blade row to the inlet plane of the next blade row, it would be a reasonable argument that the outlet velocity triangle of a blade row is the same or very similar to the inlet velocity triangle of the next blade row for the following reasons. This minimizes the onset of flow separation in the adverse pressure gradient on the suction side of each compressor blade and that in turn minimizes the onset of stall and maximizes the diffusion taking place within adjacent blades to give maximum compressor efficiency. To begin solving for the stage inlet and outlet velocity triangles, the straight forward RSRR design guideline is used to initialise the design process. This initial design assumption results in similar flow angles at the stage inlet and outlet. As the compressor design matures, the stage inlet and outlet flow angles variations are however allowed.
In the studied compressor, the axial velocity and the wheel speed are not constant throughout the compressor, implying varying velocity triangles. Wheel speed is a product of high pressure spool rotational speed and the mean radius or Eulerian radius at each stage. Each stage has been designed with a different Eulerian radius; hence, wheel speed is not constant. Attempting to obtain similar absolute velocity and relative velocity flow angles at the stage inlet and outlet is too stringent. Among the many possible departures from the RSRR design guide, this study retained only the design rule of similar relative velocity flow angles at the stage inlet and outlet, until minor changes are necessary to achieve a converged set of flow angles for all blades in all stages.
2.7 Iteration variables
Ready with all the inputs in the categories listed above, there are still two unknown flow angles that influence the flow speeds within the compressor. As the IGV flow turning angle is unknown, the absolute inlet flow angle of the first stage is also unknown. The other unknown angle is the absolute outlet flow angle at the last stage of compressor before the OGV, which is also referred to as the absolute OGV inlet angle. These flow angles will be the iteration variables to explore the design space of flow angles for each stage. When a combination of IGV flow turning angle and absolute OGV inlet flow angle returns a set of flow angles, from all the stages, where the differences between inlet velocity triangles and outlet velocity triangles are acceptably small, this set of flow angles and their corresponding flow speeds is considered a converged solution of the SUSM.
2.8 Design guidelines for uncertain information
To reduce assuming a fixed value for uncertain information, the following minimum design guidelines are implemented.
-
The axial flow speed, outer and inner radii are smooth varying in the axial direction to reduce boundary layer build up.
-
The stator and rotor blades are likely to have similar camber angles at the initial design stage. Since flow is more energetic across the rotor, the rotor blade is allowed more camber than the stator blade as the calculation progresses.
-
Stage reaction is initially assumed at 0.5 and is allowed to vary between 0.0 and 1.0.
-
The de Haller number is calculated at each stage and checked against the historical achievement of >0.72, as used in Falck's [11] design approach. Saravanamuttoo et al. [20] discusses the de Haller number as only an initial design criterion. Due to the lack of more intimate machinery details in this study, the de Haller number is sufficient for the SUSM. The diffusion factor is a detailed design criterion requiring further compressor details which may not be available.
-
The inlet velocity triangle of a stage is very similar to the outlet velocity triangle of the previous stage.
2.9 Stages without variable guide vanes
As greater compression takes place in the high pressure stages where there is typically no VGV, the SLC and flow angle relationship is examined next. At non-VGV stages, the angles of the velocity triangles at both the rotor inlet and the rotor outlet need to be fairly consistent across a range of rotational speeds, ω to achieve the intended pressure rise. This implies at the inlet and outlet stations of a blade row, the ratio of absolute speed V ABS:relative speed V REL:wheel speed U WHEEL in Figure 2 must remain similar to maintain velocity triangles of similar proportions when varying rotational speed.
The Euler whirl equation, e
WHIRL is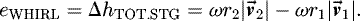 (3)
(3)
Combining the Euler whirl equation and SLC, ψ for an axial stage gives (4)
(4)
Defining wheel speed 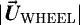 at station 1 as
at station 1 as 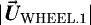 ,
,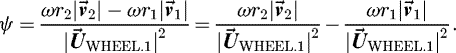 (5)
(5)
Using the wheel speeds at stations 1 and 2, and noting that ω is common since the same shaft is used,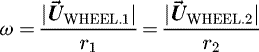 (6)a relationship between wheel speeds at different stations of varying radius is found
(6)a relationship between wheel speeds at different stations of varying radius is found
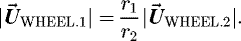 (7)SLC becomes
(7)SLC becomes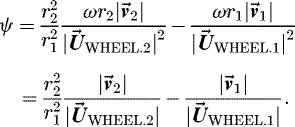 (8)
(8)
The components of absolute speed gives a relation between 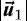 and
and 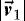 .
.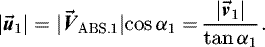 (9)
(9)
The subsequent analysis is to relate  and
and 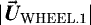 with both flow angles α and β. Using the two triangles in Figure 2 found above and below the axial velocity vector, the wheel speed,
with both flow angles α and β. Using the two triangles in Figure 2 found above and below the axial velocity vector, the wheel speed, 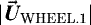 , is related to the axial speed,
, is related to the axial speed, 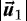 by equation (10).
by equation (10).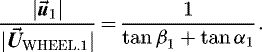 (10)
(10)
Removing 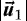 and introducing
and introducing 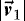 with equation (9) at station 1 gives
with equation (9) at station 1 gives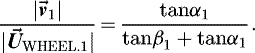 (11)
(11)
Returning to SLC in equation (8), SLC becomes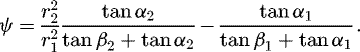 (13)
(13)
Within a non-VGV stage, equation (13) indicates that SLC depends on the flow angles and the variation between γ 1 and γ 2. Since in rear high pressure stages with no VGV capability, flow angles need to remain constant at varying rotational speed, ω, SLC is necessarily constant when varying ω at each non-VGV stage.
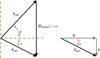 |
Fig. 2 Velocity diagram at the rotor inlet and rotor outlet. |
2.10 Building a basic axial compressor
The compressor performance data from Pedersen [21] at the highest power output is considered the design point for this axial compressor and used for inferring a possible compressor design. In the following sections, the inferred design is studied by examining the effects of implementing various design rules.
2.10.1 Inlet guide vane model
Before setting up the thermodynamic model of the compressor, the IGV is treated separately as it only turns the flow. As the IGV is a flow device with no moving parts and only smooth, gently curving walls, the blockage estimated to accumulate at the end of the IGV is assumed at 1.00%, due to boundary layer growth. From the same gas turbine manufacturer, Holloway et al. [22] report a blockage of 3% at the first rotor inlet when designing a highly loaded 10-stage axial compressor with an overall pressure ratio of 23 for aviation. With no further information, a small 0.01% of the entire specific entropy rise is assumed to take place in the IGV, with the remainder through the compressor. The IGV is also assumed to incur no flow losses given its short length and smooth gradual flow turning angle. The compressible Bernoulli equation in equation
(14) is one of the governing equations for the IGV, selected for its conservation of specific stagnation enthalpy.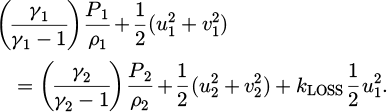 (14)
(14)
Station 1 is the IGV inlet while station 2 is the IGV outlet. The loss coefficient k
LOSS is assumed zero but should it be needed, the reference velocity is u
1 instead since this is the only known velocity and v
1 is zero at the inlet. The other governing equation is the second law of thermodynamics, where specific entropy is determined as a function of temperature and pressure.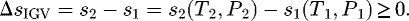 (15)
(15)
Due to flow turning, increasing rotational speed and maintaining mass flow rate, the kinetic energy increases at the expense of thermal energy and pressure through the IGV.
2.10.2 Thermodynamic model
The unknown inlet conditions of the compressor are estimated as 100 000 Pa and 278.15 K. At the compressor outlet, there is only information on stagnation temperature and static pressure. This information is transferred onto the OGV inlet, equivalent to one stator blade row ahead of the compressor outlet. The outlet static temperature is determined at the OGV inlet instead, through iteration with the help of the estimated velocity components  and
and  (u and v). The orientation of
(u and v). The orientation of 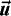 and
and 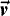 is shown in Figure 2.
is shown in Figure 2.
Viscosity and the shed wakes build up throughout the compressor, increasing blockage for the axial flow. The minimum blockage accumulated at the end of the compressor is 10.0%, based on the available flow area in Pedersen [21] and the blockage model then defines the blockage value B as 90%.
At the OGV inlet, v depends on the stator outlet flow angle, which is also an unavailable piece of information. However, v may be efficiently defined as a fraction, ku
of wheel speed from equation (16).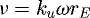 (16)
where rE
is the Eulerian radius at each blade row and
(16)
where rE
is the Eulerian radius at each blade row and 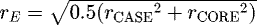 . The outlet static temperature T is found through the outlet stagnation temperature. With OGV inlet temperature and pressure determined, the specific entropy rise in the whole compressor is calculated.
. The outlet static temperature T is found through the outlet stagnation temperature. With OGV inlet temperature and pressure determined, the specific entropy rise in the whole compressor is calculated.
2.10.3 Stage loading coefficient model
In this SUSM, four possible SLC distribution models are considered. There is no preferred model as each gas turbine has its unique heritage and possibly additional stages were designed differently as evident in the account by Smith [7] for a gas turbine manufacturer.
-
Constant SLC for non-VGV stages and constant SLC for VGV stages: at each level of power output, the specific stagnation enthalpy rise through the compressor, Δh TOT.COMP with corresponding rotational speed ω is used in equation (17) to determine the SLC, ψ, distribution at that power level.
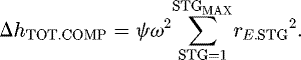 (17)
(17)
Using the set of data from Pedersen [13] with 11 power output levels and thermodynamic data from Cengel [23], the third highest power output gives the largest constant ψ at all stages. This is considered the design SLC, ψ DS.
-
Constant temperature rise for all stages: based on the highest power output, equation (18) gives the temperature at each stage outlet. The velocity at the mean line fixes the specific stage stagnation enthalpy in equation (19) and in turn, determines the design SLC for each stage, ψ DS,STG.
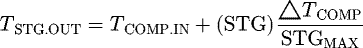 (18)
(18)
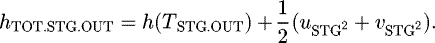 (19)
(19)
This SLC model, which is based on constant temperature rise through all stages, is inspired by a worked example in Mattingly [8], where a preliminary compressor is designed without detailed stage temperature information.
-
Constant specific static enthalpy rise for all stages: using the operating point with the highest power output, equation (20) calculates the specific stagnation enthalpy at each stage outlet, which in turn determines the design SLC for each stage, ψ DS,STG.
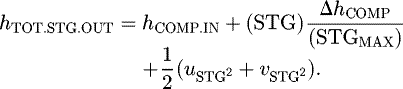 (20)
(20)
The form of the SLC model based on constant specific static enthalpy rise shares the same inspiration as the constant temperature rise SLC model and supported by a rule of thumb for constant stage energy rise in [24]. Specific static enthalpy is the variable as this is also common in turbomachinery analysis.
-
Varying (decreasing) SLC across the stages: the SLC at the last stage is a percentage lower than the SLC at the first stage, with SLC varying linearly across all the middle stages. Using the operating point with the highest power output, equation (21) gives the specific stage stagnation enthalpy rise in terms of the design SLC of each stage, ψ DS,STG. Using the specific stagnation enthalpy rise for the full compressor, equation (22) determines the design SLC of each stage.
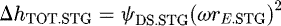 (21)
(21)
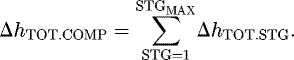 (22)
(22)
This decreasing SLC model was inspired by [25] where the front stages are deliberately highly loaded. An increasing SLC distribution may be possible too.
To determine the SLC distribution, the axial and rotational components of the absolute velocity must be known. However, these are found only after the velocity triangle analysis. Therefore, a more comprehensive solution requires iteration. To test the robustness of the solution procedure, the SLC in equation (4) is approximated by arguing that the specific stage stagnation enthalpy rise is similar to the specific stage static enthalpy rise, Δh TOT.STG ≈ Δh STG and this removes the need to iterate as Δh STG may be determined without velocity inputs.
2.10.4 Pressure ratio model
In this SUSM, three possible pressure ratio models are available, each built with an efficiency model and a specific entropy model.
-
Pressure ratio guided by small stage polytropic efficiency using reference specific entropy (function of temperature)
-
Pressure ratio guided by small stage polytropic efficiency using specific entropy (function of temperature, pressure)
-
Pressure ratio guided by fully isentropic compression based specific entropy (function of temperature, pressure)
Each pressure ratio model suggests a feasible relative distribution of maximum stage pressure ratios for all the stages. There is no best model as pressure ratio is determined stage by stage to meet the overall pressure ratio, which in turn fulfills several possible objectives. The gas turbine could have been designed for maximum overall pressure ratio or the most economical maintenance package. An inference using the overall pressure ratio is at best an estimate and cannot compensate for unavailable information, considering that an actual design has as many as a million details as pointed out by Ghisu et al. [2].
In pressure ratio model 1, the actual specific stage entropy rise is not known beforehand. However, the stage efficiency may be approximated by the compressor's polytropic efficiency (23), with a mean γ, 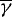 determined from the conditions at the inlet and outlet of the compressor.
determined from the conditions at the inlet and outlet of the compressor. (23)
(23)
The specific stage outlet static enthalpy, h
2 and the specific stage isentropic outlet static enthalpy, h
2s
lie on the same isobar on the h–s diagram, experiencing the same pressure rise. To avoid the still unknown actual specific stage entropy rise, isentropic compression calculation is carried out with h
2s
. The specific entropy rise in equation
(24) is set to zero and using T
2s
= T(h
2s
), a feasible stage pressure ratio is estimated from P
2/P
1.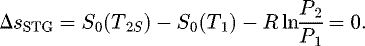 (24)
(24)
The specific reference entropy s 0 is from the thermodynamic table for air from Cengel [23].
Pressure ratio model 2 is similar to pressure ratio model 1 except specific entropy is a function of temperature and pressure based on the s–T–P chart by Aartun [26]. Using the stage inlet temperature, T
1 and the stage isentropic outlet temperature, T
2S
the specific entropy rise in equation (25) determines the stage pressure ratio, P
2/P
1.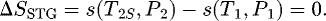 (25)
(25)
In pressure ratio model 3, knowing that for a given temperature rise, T
1–T
2, the maximum pressure rise occurs when the specific entropy rise is zero. With available inlet and outlet temperatures from the selected SLC model, specific entropy is found as a function of temperature and pressure based on the s–T–P chart by Aartun [26]. Equation (26) determines the maximum stage pressure ratio, P
1/P
2.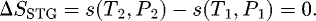 (26)
(26)
The actual stage pressure ratio is lower than maximum stage pressure ratio, and in this way, accounts for the specific stage entropy rise. The specific stage entropy rise is proportional to the maximum pressure rise in a stage for the same stage efficiency and assuming nearly linear isobars on the T–s diagram. In this way, the stage losses are distributed according to the stage compression capability. The lower actual pressure ratio is also determined in such a way that a smooth axial velocity distribution results at the front of the compressor. All stages are subjected to the same fraction except the first stage. In the studied compressor, the same fraction kPR
is applied on stages 2 to 16 and kPR
,1 for stage 1. The iteration variable is kPR
. Each guessed kPR
is automatically constrained by equation (27) such that all stage pressure ratios achieve the overall pressure ratio of the compressor, OPR as kPR
,1 takes the slack.
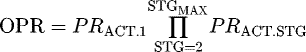 (27)where
(27)where 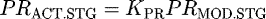 and
and 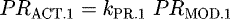 .
.
Next, the stage temperature, gas law and mass flow rate conservation determine the no-blockage axial velocity at each stage outlet. Iteration continues till the no-blockage velocity distribution from stage 1 to stage 3 varies linearly with compressor axial coordinate x, in a straight line fit of 3 points. The no-blockage velocity was selected as it depends only on geometry since the boundary layer build up is assumed small at the beginning of the compressor.
2.10.5 Blockage model
Blockage in a gas turbine compressor is challenging to define accurately due to the accumulation of wakes from multiple bodies interrupting the flow. Falck's [11] LUAX-C design code suggests that the blockage increases at 0.5% per stage and stabilises after stage 8. This idea was adapted to give blockage models 1 and 2 in Figure 3. The final blockage was set to 10% for both a smooth and abrupt transition at about stage 8. The data from Pedersen [21] indicates that the maximum available flow area through the compressor follows a steep “s” shaped curve and reaches a steady level of 90% availability in cross-section area in the last few stages of the compressor and is designated as blockage model 3 in Figure 3.
 |
Fig. 3 Blockage models in this study. |
2.10.6 Velocity triangle model
The velocity triangles of the last stage of this compressor are determined first since at the outlet of the last stage, all the flow quantities are known. Based on the analysis of non-VGV stages in Section 2.9, non-VGV stages require similar velocity triangles which in turn need similar SLC. Solving from the last stage to the first stage results in more similar flow angles in the last stages as departures from the RSRR design guide are admitted only at the front stages. This approach is found to ease solution convergence difficulties.
For each stage, the solution is a set of blade angles and flow angles where the Euler whirl matches the specific stagnation enthalpy rise, where the de Haller number is met for both rotor and stator and the stage reaction is reasonable. The stage reaction is initially 0.5 and allowed to vary as iteration proceeds. The rotor blade is given more curvature than the stator blade as the solution iterates.
At each stage, the solution process begins at the stage outlet, where specific stagnation enthalpy, the flow velocities, blade angles and thermodynamic properties are found. Moving to the stage inlet, this SUSM applies only initially the design rule of similar relative velocity flow angles at the stage inlet and outlet, β
1 = β
3. The β
1 angle enables determining the stage inlet flow angles, blade angles and thermodynamic properties. The rotor-stator interface quantities in the middle of the stage are determined by degree of reaction, R
REAT in equation (28),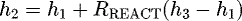 (28)
(28)
and conservation of specific stagnation enthalpy across stator in equation (29). This sets up the specific static enthalpy and specific stagnation enthalpy to determine the absolute velocity.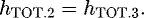 (29)Using the absolute velocity, the rotor–stator interface blade angles and thermodynamic properties are found. With all flow angles and thermodynamic properties available, the stage Euler whirl in equation (3) is the “hard” criteria used to test the suitability of stage reaction and inlet relative velocity angle. The first “soft” criterion is the stage degree of reaction, which ranges about 0.5 for the axial compressor in this study. The next “soft” criteria are the difference in blade angles, Δθ from blade angles,
(29)Using the absolute velocity, the rotor–stator interface blade angles and thermodynamic properties are found. With all flow angles and thermodynamic properties available, the stage Euler whirl in equation (3) is the “hard” criteria used to test the suitability of stage reaction and inlet relative velocity angle. The first “soft” criterion is the stage degree of reaction, which ranges about 0.5 for the axial compressor in this study. The next “soft” criteria are the difference in blade angles, Δθ from blade angles, 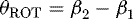 and
and 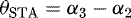 .
.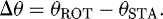 (30)
(30)
The de Haller number, 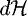 is the last “soft” criteria, which is a ratio of relative outlet speed to relative inlet speed for the rotor blades and absolute outlet speed to absolute inlet speed for the stator blades.
is the last “soft” criteria, which is a ratio of relative outlet speed to relative inlet speed for the rotor blades and absolute outlet speed to absolute inlet speed for the stator blades.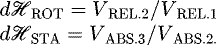 (31)
(31)
Since there is insufficient design information to allow a direct calculation of the flow and blade angles, a suitable range of values are accepted for the design variables, R
REACT, Δθ are dℋ, according to the design guidelines for uncertain information in Section 2. Being a “hard” criteria, Euler whirl, e
WHIRL is used in an error variable ε
HARD in equation (32) to iteratively suggest a Δθ that results in an Euler whirl which matches the specific stage stagnation enthalpy rise.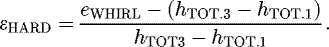 (32)
(32)
Consequently, the stage degree of reaction is also affected and is updated with another error variable ε
SOFT in equation (33).
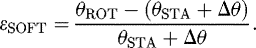 (33)
(33)
When the stage degree of reaction and acceptable angle difference Δθ between the rotor and stator blade angles do not result in feasible set of blade and flow angles, the inlet relative flow angle β
1 is adjusted with the ε
HARD error variable. The design variables V
DS are updated with their error variables ε and a relaxation factor, f
RELAX to prevent over-correction, according to equation (34).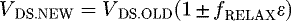 (34)where the subscripts “NEW” and “OLD” refer to the updated and previous values, respectively.
(34)where the subscripts “NEW” and “OLD” refer to the updated and previous values, respectively.
3 Results
A basic axial compressor from Section 2.10 is “designed” with the following inputs to study the influence of the IGV flow turning angle, the OGV inlet angle, the pressure ratio models and the SLC models. The SLC is constant for the non-VGV stages and also constant SLC for the VGV stages (SLC model 1). The distribution of stage pressure ratios is based on fully isentropic compression using specific entropy as a function of temperature and pressure applied to each stage (pressure ratio model 3). The blockage from boundary layer shedding off the blades as wakes and stationary wall boundary layers is set to grow to a maximum of 10% of the cross-sectional area, using blockage model 1. The “design” goal is to reduce the mean amount of mismatch in flow angles at the stage-outlet–stage-inlet interfaces. The simplified solution procedure, where, the specific stage stagnation enthalpy rise is assumed similar to the specific stage static enthalpy rise, 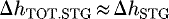 is used to remove the need to iterate, sacrificing improved results for speed.
is used to remove the need to iterate, sacrificing improved results for speed.
Using the stage un-stacking approach in Section 2, a large collection of data is generated for a range of IGV flowing turn angles and OGV inlet flow angles (before the OGV straightens the flow), to locate the design space where the mismatches in flow angles at each stage interface is minimal. This would indicate a possible axial compressor design at the operating point.
3.1 Effect of increasing IGV flowing turn angle
To study the effect of increasing the IGV flow turning angle, Figure 4 shows the data generated for IGV flowing turn angles from 20° to 34° and for selected rotational components of the absolute velocity at the OGV inlet. The rotational component v is a fraction, varying from 0.42 to 0.52, of the OGV inlet wheel speed, defined in equation (16). Each data point represents a set of design choices that results in a feasible set of flow angles for the whole compressor.
As both the IGV flow turning angle and v, the fraction of wheel speed, increase towards the optimum combination of IGV flow turning angle of about 31° and v close to 0.46 of the OGV inlet wheel speed, it becomes possible to obtain a set of feasible flow turning angles for the axial compressor as a whole that achieves minimal mismatch in flow angles at each stator-outlet–rotor-inlet interface between stages. However, as the fraction of wheel speed increases further, it again becomes increasingly difficult to obtain a set of feasible flow turning angles for the whole compressor. Since the axial compressor's design is highly optimized, the many design parameters simultaneously match narrowly only about the design point.
 |
Fig. 4 The effect of flow turning angle in the IGV on the mean mismatch in flow angles per stage at each stator-outlet–rotor-inlet interface. |
3.2 Effect of OGV inlet flow angles
The velocity components u and v at the OGV inlet determine the outlet flow angle at the last stage's stator. An improved estimate of the specific stagnation enthalpy at the OGV inlet requires the rotational component v before allocating sufficient specific static and stagnation enthalpy to each axial compressor stage. Using the same generated data for IGV flow turning angles, the effect of OGV inlet flow angle is examined by varying v and presented in Figure 5. Each data point in Figure 5 represents a set of design choices that results in feasible set of flow angles across the whole compressor. For clarity, only the even IGV flow turning angles are shown.
Increasing v as a fraction of wheel speed at the outlet has only a small effect on reducing the amount of mismatch in flow angles at the stator-outlet–rotor-inlet interface. Adjustments to v hardly minimise the flow angle mismatches unless the IGV flow turning angle is close to 31° for this axial compressor.
 |
Fig. 5 The effect of increasing v as a fraction of wheel speed at the OGV inlet on the mean mismatch in flow angles per stage at each stator-outlet–rotor-inlet interface. |
3.3 Effect of pressure ratio model
The effects of different pressure ratio models on an axial compressor's flow angles at the design point are examined with a basic compressor from Section 2.10, where the IGV flow turning angle is 28° and at the OGV inlet, v = 0.45 of the wheel speed. The SLC model 1 sets the axial temperature distribution, assuming 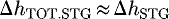 . The combined effect of the choice of pressure ratio model and the method that smooths the velocity distribution has minimal effect on the mean flow angle mismatch at the stator-outlet–rotor-inlet interfaces as seen in Figure 6. The pressure ratio models only distribute available pressure among the stages of the axial compressor. Within the overall compression ratio of this axial compressor, any additional rise in pressure ratio in a stage is compensated with a lower pressure ratio in another stage. For example, the lower pressure ratios at the rear stages suggested by pressure ratio model 3 are complemented by higher pressure ratios in the front stages and the reverse occurs pressure ratio models 1 in Figure 7B.
. The combined effect of the choice of pressure ratio model and the method that smooths the velocity distribution has minimal effect on the mean flow angle mismatch at the stator-outlet–rotor-inlet interfaces as seen in Figure 6. The pressure ratio models only distribute available pressure among the stages of the axial compressor. Within the overall compression ratio of this axial compressor, any additional rise in pressure ratio in a stage is compensated with a lower pressure ratio in another stage. For example, the lower pressure ratios at the rear stages suggested by pressure ratio model 3 are complemented by higher pressure ratios in the front stages and the reverse occurs pressure ratio models 1 in Figure 7B.
The choice of pressure ratio model, however, does affect the maximum pressure ratio available at each stage as seen in Figure 7A, where pressure ratio model 3 delivers more compression in the front stages compared to pressure ratio model 1 and 2. This effect is present in a small way in the actual stage pressure ratios in Figure 7B. The estimated stage pressure ratio is closer to the actual from only stage 5 onwards. The “PR GE LM2500” data in Figure 7B is taken from Klapproth et al. [15].
The resulting axial velocity profile in Figure 8 is smooth at the front stages even after factoring the effect of blockage. However, when moving from the last VGV stage to first non-VGV stage, there is a rougher transition. This would happen as this SUSM has no provision for transiting the flow from a VGV stage to a non-VGV stage. For the same mass flow rate, the axial velocity distribution from pressure ratio model 3 in Figure 8 does indicate lower axial velocities, implying higher density from higher pressure ratios in the front stages.
Considering that the actual axial velocity distribution (“Act. Ax. Vel.” in Fig. 8) from Klapproth et al. [15] is not always smooth, the rough transition in axial velocity is acceptable. According to the approximate compressor schematic on the gas turbine manufacturer's marketing datasheet [14], there is a proportionally longer stator at stage 8. The 8th stage stator houses the bleed air valve, according to Klapproth et al. [15]. In the non-VGV stages, the axial speeds show the greatest difference. This difference is traced to several possible sources, the OGV, bleed air, annulus cross-sectional area and blockage.
The OGV is mentioned by Klapproth et al. [15] but there is too little information on the cross-sectional area and the axial length for a proper analysis of the flow speed. Should the OGV be part of the analysis, it would contribute only a small pressure rise. The OGV would only very mildly reduce the stage loading at all stages as a small pressure and temperature rise is obtained through straightening the flow. The corresponding mild reduction in stage compression would give lower stage density at the last stages and the axial speeds would increase to maintain the same mass flow rate. Therefore, the OGV excluded from the analysis is not a cause of higher axial flow speed at the last stages. In addition, inferring the radius from the same approximate compressor schematic on the gas turbine manufacturer's marketing datasheet [14], there is little change in cross-sectional area after the last compressor stage, implying axial mass flux might keep constant after flow straightening. Since pressure increases to give higher density through the OGV, lower axial speed results after the OGV to maintain mass flow rate. This would not affect the axial speeds of the last compressor stages. Bleed air for film cooling in the high pressure turbine is interpreted as obtained from the compressor discharge according to the technical section of this 3rd party market analysis [27], and does not affect the axial speed at the last stages. Similar no-blockage annulus cross-sectional area is found by estimating the radius from the same approximate compressor schematic on the manufacturer's marketing datasheet [14] and using data in Pedersen [13]. The estimated radius from the same approximate compressor schematic on the manufacturer's marketing datasheet [14] results in a slightly larger annulus cross-sectional area. The blockage model supported by data in Pedersen [21] shows a clear 10% reduction in available cross-sectional area after stage 9 as indicated in Figure 3. This level of blockage is used at the OGV inlet. To resolve this obvious difference in axial speed in the 2nd half of the compressor especially at the OGV inlet, certain modelling improvements are possible. The extraction of bleed air must be considered and a better estimated annulus cross-sectional area is needed. As the analysis is at the design operating point and approximate, further information on the VGV operation from Klapproth et al. [15] for this gas turbine is not used.
For the same SLC model, the rotor blade row needs to deliver a similar specific stage stagnation enthalpy rise in all three pressure ratio models. When pressure ratio model 3 delivers lower stage axial velocity (Fig. 8) compared to the other pressure ratio models, the rotor needs to turn the flow by a greater angle to deliver a larger rotational component of the absolute velocity that compensates for the reduced axial component of the absolute velocity, according the Euler whirl equation. This leads to pressure ratio model 3 generating slightly larger rotor blade angles compared to the other pressure ratio models in Figure 9A. Consequently, since the rotor blade row is delivering a larger rotational component of absolute velocity with pressure ratio model 3, and the stator blade row need only conserve specific stagnation enthalpy, the inlet and outlet velocity triangles of the stator blade row are more similar. Consequently, the stator blade angles are slightly smaller compared to that obtained in the other pressure ratio models in Figure 9B.
In the actual compressor, by the same argument, the much lower axial speed will result in larger blade cambers, resulting in differences between the blade cambers obtained in this stage unstacking method and the actual (“Tip Camber” and “Hub Camber” in Fig. 9).
By deliberate design in this SUSM, the β 1 angle is consistent or allowed to vary only slightly across the stages. Since the β 1 angle could keep constant in Figure 10A with only slight variations at the first 3 stages to accommodate determining the other flow angles, this assumed β 1 design guide is feasible. Assuming that the effects of the RSRR initial design persist after many design iterations, the α 1 angle would also likely be as consistent as β 1 at each stage. Without constraining the α 1 angle, this SUSM has determined a distribution of α 1 angles that is relatively consistent, if not smoothly varying, especially for the non-VGV stages. It is possible that the studied axial compressor shows signs of the RSRR initial design, especially for the non-VGV stages. Similar to the β 1 angle, the α 1 angle varies smoothly in Figure 10B. The α 2 and β 1 angles from stage unstacking are much closer to the actual. Should lower axial speed be used at the last stage, the last stage β 1 angle would be larger. Since this stage unstacking method has the capability to slightly reduce the β 1 angle as the analysis proceeds towards the front of the compressor, it would be possible that beginning with a larger β 1 angle at the last stage, this SUSM is able to estimate a β 1 angle distribution closer to the actual.
 |
Fig. 6 Comparison of mean flow angle mismatch between pressure ratio models. |
 |
Fig. 7 Maximum pressure ratios and used Pressure ratios with different pressure ratio model (stage outlets indicated by numbers in italics). |
 |
Fig. 8 Stage axial velocity with different pressure ratio models (stage outlets indicated by numbers in italics). |
 |
Fig. 9 Blade angles with different pressure ratio models. |
 |
Fig. 10 Flow angles with different pressure ratio models. |
3.4 Effect of SLC distribution
The effects of different SLC models on an axial compressor's flow angles at the design point are examined with the same basic compressor from Section 2.10, except that pressure ratio model 3 is used and the SLC model varies. The IGV flow turning angle is still 28° and at the OGV inlet, v = 0.45 of the wheel speed.
Compared to the different pressure ratio models, the choice of SLC model has a larger effect on mean flow angle mismatch at the stator-outlet–rotor-inlet interfaces than for the choice of pressure model as seen in Figure 11. Using these design options, the SLC model 3, where there is a constant specific static enthalpy rise for all stages could not support generating a complete feasible set of flow angles that fit all stages. While generating the velocity triangles from the OGV inlet to the inlet with SLC model 3, the available energy and requirements could not set up a proper velocity triangle at a middle stage within this axial compressor.
The stage SLC distribution in Figure 12 shows that model 3 with constant specific stage static enthalpy rise has the lowest SLCs for the non-VGV stages. The compressor designed with SLC model 3 imparts lesser specific stagnation enthalpy to the working fluid when higher rotational kinetic energy (ωrE ) is available at the rear stages. At the same time, the front stages must impart higher specific stagnation enthalpy to the working fluid when lesser rotational kinetic is available as the Eulerian radius, rE is smaller.
The specific stage static enthalpy rise in Figure 13 shows the same trend as stage SLC since the simplifying assumption that 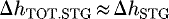 is used in the SLC definition. Because SLC model 3 could not support in finding a complete set of flow angles for the whole axial compressor, the specific stage static enthalpy distributions in SLC models 1, 2 and 4 indicate that specific stage static enthalpy rise must increase stage after stage for this axial compressor. The specific stage static enthalpy rise in model 2 is not a smooth curve as the temperature-specific static enthalpy function is only sufficiently piecewise smooth.
is used in the SLC definition. Because SLC model 3 could not support in finding a complete set of flow angles for the whole axial compressor, the specific stage static enthalpy distributions in SLC models 1, 2 and 4 indicate that specific stage static enthalpy rise must increase stage after stage for this axial compressor. The specific stage static enthalpy rise in model 2 is not a smooth curve as the temperature-specific static enthalpy function is only sufficiently piecewise smooth.
In this SUSM, the stage pressure ratios cannot be fixed while varying the stage load coefficient because only the variation in pressure ratios is available for smoothing the axial velocity especially from the IGV to the 2nd stage of the axial compressor. However, the difference is stage pressure ratios in Figure 14 are small from stage 5 onwards. The major difference is found in stages 1–4, where higher specific static enthalpy rises (Fig. 13) correspond to higher pressure ratios (Fig. 14).
Since the compressor inlet axial speed is known, each SLC model works with the same pressure ratio model to generate the same inlet density, resulting in pressure and temperature moving in tandem at the inlet. In the subsequent stages, for the same mass flow rate and known smooth cross-sectional area variation, a smooth density variation is needed to generate a smooth axial velocity profile. This smooth density variation further maintains the differences in pressure ratio for the front few stages.
By the 2nd stage in the axial compressor, Figure 15 shows that the axial velocity is no longer influenced by the conditions at the compressor inlet. In SLC model 1, due to the initial lower pressure ratios, the resulting lower density flow is compensated by increasing the axial velocity through the rest of the axial compressor. The opposite occurs for SLC model 3, which has the highest initial compression of the 4 SLC models.
 |
Fig. 11 Comparison of mean flow angle mismatch between SLC models. |
 |
Fig. 12 Stage SLC distribution with different SLC models. |
 |
Fig. 13 Specific stage static enthalpy rise with different SLC models. |
 |
Fig. 14 Stage pressure ratios with different SLC models. |
 |
Fig. 15 Stage axial velocity with different SLC models. |
4 Discussion
This SUSM is applied to the design operating point only. The actively adjustable design options are the choice of SLC model, pressure ratio model, blockage model and amount of blockage. These factors work through the method to determine the overall specific stage static enthalpy rise, stage pressure ratios and axial velocity profile through the axial compressor. These in turn determine velocities and flow angles within each stage of the axial compressor, which in turn determine the amount of flow angle mismatch.
4.1 IGV flow turning angle
While the implemented design options have identified a design space where a range of inputs are able to generate zero flow angle mismatches between the stages, the most influential design option that reduces angle mismatches to zero is the IGV flow turning angle.
In terms of reducing the mean mismatches in flow angles per stage, varying the OGV inlet flow angle by varying v as a fraction of wheel speed at the OGV inlet exerts little influence. In this LM2500 compressor, increasing v causes no increase in OGV inlet specific stagnation enthalpy since the compressor's outlet stagnation temperature is fixed. However, increasing v reduces the specific static enthalpy only slightly as the velocity contribution to specific stagnation enthalpy is small. A 10% increase in v from 42% to 52% of wheel speed at the OGV inlet results in only about 0.05 kJ/kg change in specific stagnation enthalpy at the stage before the OGV inlet. Furthermore, beyond this small 10% range of v, there are either no feasible sets of flow angles for the whole compressor or the flow angle mismatch cannot reach zero.
In contrast, adjusting the IGV flow turning angle exerts a greater influence on reducing the mean mismatches in flow angles per stage. For solutions surrounding the optimum IGV flow turning angle that results in zero flow angle mismatches across all stages, a 1° increase in IGV flow turning angle causes a 0.2–0.5 kJ/kg specific static enthalpy drop at the IGV outlet. For a more quantitative comparison, a 3° change about the optimum IGV flow turning angle of about 31° (≈10% change) causes about 0.6–1.5 kJ/kg change in specific stagnation enthalpy, at the IGV outlet (stage 1 inlet), which is easily 10 times greater than the specific static enthalpy changes implemented at the OGV inlet.
Determining matching flow angles between stages and for the Euler whirl to match the specific stagnation enthalpy rise at each stage for all 16 stages of this compressor is akin to simultaneously satisfying 32 sets of requirements. These requirements and the compressor's overall pressure and temperature ratios are therefore actually coupled together to characterize the design of the studied axial compressor. This large number of constraints naturally greatly narrows the solution range of both the IGV flow turning angle to near 31° and v to about 0.46 of the OGV inlet wheel speed for this axial compressor. However, as v at the OGV inlet has much lesser influence on flow angle mismatches than the IGV flow turning angle, the angle mismatches are efficiently first reduced by adjusting the IGV flow turning angle and if needed, followed by fine tuning with v at the OGV inlet.
4.2 Pressure ratio distribution
Smith [7] documents the rich design heritage of this gas turbine which has experienced 2 rounds of stage additions at the rear. While there is little doubt of an improved understanding of the underlying physics of flow and of materials, the account by Smith [7], shows instead that the proven aspects of the current design are retained in the interest of reliability when adding more stages. Wadia et al. [16] report the most recent addition of the 0th stage to the front of the compressor where little of the original gas turbine is altered. This implies that the design approach is possibly not consistent in all aspects across the compressor. In Figure 16, the shape of the pressure ratio distribution curve of the studied compressor is compared to another compressor by the same manufacturer “PR GE NASA EEE” referred to by Bruna et al. [28] and a similar 17 stage machine (PR Hitachi 17 stg) by Kashiwabara et al. [25]. The inlet is 0 and the compressor outlet is 1 on the horizontal axis.
The GE LM2500 and Hitachi 17-stage are land based turbines. In the design of the Hitachi 17-stage compressor, the front 3 stages are highly loaded [25]. The GE LM2500 compressor does not deliberately load the front stages. While the design perspectives differ, the stage pressure ratio distributions are similar with a peak in pressure ratio at one of the front stages. The “GE NASA EEE” refers to the Energy Efficient Engine (EEE) and is meant to support aviation engine development. The detailed design phase of compressor of the “GE NASA EEE” began with specifying the specific stagnation temperature rise at each stage for the design operating point seen in Figure 14 from Holloway et al. [22]. This distribution was overall decreasing with stage number except the middle stages 6 and 7, where the decrease was more obvious. The initial distribution of the stage static temperature rise in Figure 27 from Holloway et al. [22] is similar. In the final configuration, the static temperature distribution through the stages did not change too much as seen also in Figure 27 from Holloway et al. [22]. While the “GE NASA EEE” pressure ratio was not specified directly, it synchronizes closely with the temperature variation. Therefore, the distribution of stage pressure ratio is a design choice, driven by temperature variation and therefore SLC.
These 3 designs show that aggressive compression in the early stages is more feasible than in the later stages. The important detail is which stage then delivers the highest pressure ratio. The absolute pressure rise of the first stage in the EEE would be smaller than that of the other two compressors, since the EEE design operates primarily in a low ambient pressure environment of 22 631.264 Pa at 11 km altitude according to Frei's [29] online atmospheric pressure calculator. However, more pressure ratio distributions from actual compressors are needed before a firm design guideline may be constructed.
The pressure ratio models, and their supporting SLC models, suggested so far are suited only for preliminary analysis. The difference between the shapes of the pressure ratio distribution curves estimated in Figure 7B and the actual in Figure 16 can only be resolved with a more comprehensive SLC distribution. For this LM2500 compressor, the axial temperature distribution is not available. This impedes inferring the actual SLC distribution. A clear improvement to this SUSM is in the SLC models. A more realistic SLC distribution inferred for the LM2500 compressor is shown in Figure 17 and this is based on the stage pressure ratios in Figure 16. This distribution contains details that presented simpler SLC models do not have, hence the differences between the estimated and actual stage pressure ratios.
 |
Fig. 16 Pressure ratio distribution of selected gas turbines. |
 |
Fig. 17 Estimated SLC distribution for the compressor in the LM 2500 gas turbine. |
4.3 Acceptable range for camber angles
In a worked example in Mattingly [8], the RSRR approach is applied to stage stack an axial compressor, generating a large database of possible values for the design variables. The difference between the inlet and outlet flow angles of a blade row ranged from 7° to 30°. For an NACA 65, a = 1.0 series airfoil, this translates to a camber of 1.53% to 6.58% of the chord where the camber lines are circular arcs. Noting that incidence angles and deviation angle are usually small at the design operating point, the estimated blade angles from this SUSM are well within this range.
While solving for the stage flow angles, a stage with a relatively higher stage axial velocity makes for less, therefore easier, rotational velocity contributions to specific stagnation enthalpy, which in turns requires less flow turning in the rotor blade row. This eventually lowers the blade curvature and consequently also lowers the tendency for boundary layer growth and separation on the suction surface.
The flow features surrounding the blades are described in relatively greater detail in Test Case E/CO-1 by Serovy and Dring [30], Test Case E/CO-3 by Ginder and Harris [31] and Test Case E/CO-5 by Serovy and Dring [32] for the purpose of bench marking computational fluid dynamics codes. The blade curvature angles used in the blade rows of the three relevant test cases are calculated across the span in the radial direction and shown in Table 1. The estimated blade angles from this SUSM are also well within this range.
Span wise radial mean blade curvature angles.
4.4 Selected stage loading coefficient and pressure ratio models
The pressure ratio distribution of the LM2500 spans a relatively small range indicating that the loading on each stage appears similar. Currently, SLC Model 1 represents this best. For the same SLC distribution, the pressure ratio model 1 gives a slightly more balanced distribution across all stages. The blockage model is 1. However, this suggested SLC distribution is more appropriately considered an initial well-informed estimate.
5 Conclusion
This paper presents an SUSM that determines the velocities and flow angles within a multistage axial compressor. The design options in this method are built upon inferred possible design guidelines implemented in actual gas turbines. The design options are implemented in four SLC models, three pressure ratio models and three blockage models which, working with other required information, determines the stage velocities and stage flow angles for an axial compressor operating at design point. The method implements a calculation procedure that simultaneously fulfills thermodynamic requirements, velocity triangle requirements and user-selected design options for the whole axial compressor at the mean line. The outputs are specific static enthalpy, pressure, axial velocity and flow angles at each stage interface of the axial compressor. The SUSM is tested with a set of operation data from an actual aero-derivative gas turbine. Through adjusting of the IGV flow turning angle and OGV inlet flow angle, the method identifies a small range of design options that suggests an axial compressor with minimal mismatch of flow angle at each stage interface. Among the adjustable design options, the method shows that the IGV flow turning angle has the most influence on minimising flow angle mismatches compared to the other design options.
Nomenclatures
Uppercase
A : Station cross sectional area (m2)
B : Blockage in terms of fraction of available station cross sectional area for flow (dimensionless)
D : Diffusion factor, a measure of the blade loading (dimensionless)
J : Mechanical equivalent of heat, 778.2 ft-lb/Btu or 1 J/J where 1 ft-lb = 1.35582 J and 1 Btu = 1055.06 J (dimensionless)
OPR : Overall pressure ratio of the compressor (dimensionless)
P : Absolute pressure in Pascal (Pa)
PR MOD : Stage pressure ratio determined from the pressure ratio models (dimensionless)
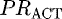 :
Actual stage pressure ratio used (dimensionless)
:
Actual stage pressure ratio used (dimensionless)
R : Gas constant for air (J/kg.K)
R REACT : Stage degree of reaction (dimensionless)
ψ : The stage load coefficient (dimensionless)
ψ DS : The design SLC, which could be a single value for all stages or a distribution of values by stage (dimensionless)
T : Absolute temperature in Kelvins (K)
U ⃗ WHEEL : The rotor tangential speed, also referred to as wheel speed U WHEEL (m s−1)
V ⃗ ABS : The absolute velocity in the velocity triangles for turbo-machinery analysis and also referred to as V ABS (m s−1)
V ⃗ REL : The free stream velocity outside the boundary layer, which is the velocity relative to the blade and is the relative velocity in the velocity triangle analysis for turbo-machinery and also referred to as V REL (m s−1)
V ⃗ DS : The general symbol for a design variable (depends on variable)
Lowercase
C P : Specific heat of air at constant pressure (J/kg.K)
C V : Specific heat of air at constant volume (J/kg.K)
f RELAX : The general symbol for a relaxation factor (dimensionless)
k LOSS : The coefficient of loss for flow in the Bernoulli equation (dimensionless)
KPR : Actual fraction of the stage pressure ratio found in the pressure ratio models (dimensionless)
KPR. 1 : The KPR for stage 1 of the compressor (dimensionless)
Ku : The fraction of wheel speed at the OGV inlet (dimensionless)
S O : Specific reference entropy from thermodynamic tables (J/kg.K)
u
⃗
or u
:
The axial component of 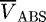 also referred to as u (m s−1)
also referred to as u (m s−1)
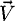 or V:
The tangential component of
or V:
The tangential component of 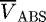 also referred to as V⃗ (m s−1)
also referred to as V⃗ (m s−1)
x : Axial coordinate of the compressor (m)
Greek
α
:
The flow angle of the  makes with the axial direction in velocity triangle analysis for turbo-machinery (°)
makes with the axial direction in velocity triangle analysis for turbo-machinery (°)
β
:
The flow angle of the 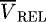 makes with the axial direction in velocity triangle analysis for turbo-machinery (°)
makes with the axial direction in velocity triangle analysis for turbo-machinery (°)
γ : The ratio of specific heats, CP /CV (dimensionless)
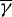 :
Mean ratio of specific heats between two or more stations in the compressor (dimensionless)
:
Mean ratio of specific heats between two or more stations in the compressor (dimensionless)
∊: The general symbol for an error variable (dimensionless)
n : Thermodynamic efficiency (dimensionless)
θ ROT : The angle of the curvature of the rotor blade (°)
θ STA : The angle of the curvature of the stator blade (°)
Δθ : The difference in angle of curvature of the rotor and stator blade (°)
ρ : Density of the working gas which is air in this study (kg/m3)
σ : Blade solidity which is the ratio of chord to pitch (dimensionless)
ω : Shaft rotational speed (rad/s)
Script
dℋ : The de Haller number (dimensionless)
Subscript
1: The blade leading edge which is also considered to be equivalent to the upstream measuring station of the blade row or blade row inlet station
2: The blade trailing edge which is considered to be equivalent to the downstream measuring station of the blade row or blade row outlet station
CFD: Computational fluid dynamics
HARD: Strict or fixed conditions or criteria
MAX: Maximum value of a variable
MIN: Minimum value of a variable
NEW: Updated values of a design variable
OLD: Previous values of a design variable
SOFT: Less strict or flexible conditions or criteria
SUSM: Stage un-stacking method
TOT: Total or stagnation properties
Acknowledgements
The authors would like to acknowledge the support of Lloyd's Register Singapore, Energy Research Institute @ NTU (ERI@N) and Singapore Economic Development Board (EDB), under the EDP-IPP programme in undertaking this work.
References
- N.A. Cumpsty, Some lessons learned, J. Turbomach. 132 (2010) 041018-1 [Google Scholar]
- T. Ghisu, G.T. Parks, J.P. Jarrett, P.J. Clarkson, An integrated system for the aerodynamic design of compression systems-part I: development, J. Turbomach. 133 (2011) 011011-1 [Google Scholar]
- T. Ghisu, G.T. Parks, J.P. Jarrett, P.J. Clarkson, An integrated system for the aerodynamic design of compression systems-Part II: application, J. Turbomach. 133 (2011) 011012-1 [Google Scholar]
- J.P. Jarrett, T. Ghisu, Balancing configuration and refinement in the design of two-Spool multistage compression systems, J. Turbomach. 137 (2015) 091008-1 [CrossRef] [Google Scholar]
- A. Sehra, J. Bettner, A. Cohn, Design of a high-performance axial compressor for utility gas turbine, J. Turbomach. 114 (1992) 277–286 [CrossRef] [Google Scholar]
- J.P. Smed, F.A. Pisz, J.A. Kain, N. Yamaguchi, S. Umemura, 501F compressor development program, J. Turbomach. 114 (1992) 271–276 [CrossRef] [Google Scholar]
- L.H. Smith, Axial compressor aerodesign evolution at general electric, J. Turbomach. 124 (2002) 321–330 [CrossRef] [Google Scholar]
- J.D. Mattingly, Turbomachinery, in: J.J. Corrigan, J.W. Bradley (Eds.), Elements of Gas Turbine Propulsion, International Edition, McGraw Hill Book Co., Singapore, 1996, Chap. 9, pp. 615–756 [Google Scholar]
- J.D. Mattingly, W.H. Heiser, D.T. Pratt, Engine component design: rotating turbomachinery, in: J.S. Przemieniecki (Ed.), Aircraft Engine Design, 2nd edn., AIAA Education Series, AIA, Reston, Virginia, USA, 2002, Chap. 8, pp. 253–324 [CrossRef] [Google Scholar]
- R.J. Steinke, STGSTK: A Computer Code for Predicting Multistage Axial Flow Compressor Preformance by a Meanline Stage Stacking Method, NASA Technical Paper 2020, 1982 [Google Scholar]
- N. Falck, Axial flow compressor mean line design, M.Sc. thesis, Department of Energy Sciences, Lund University, Lund, Sweden, 2008 [Google Scholar]
- D. Perrotti, Two dimensional design of axial compressor − an enhanced version of LUAX-C, M.Sc. thesis, Department of Energy Sciences, Lund University, Lund, Sweden, 2013 [Google Scholar]
- A. Pedersen, Ignition probability of a flammable mixture exposed to a gas turbine, Project Report for M.Sc. Programme, Department of Energy and Process Engineering, NTNU, Trondheim, Norway, 2005 [Google Scholar]
- GE Marine, LM2500+ marine gas turbine data sheet, GE, Cincinnati, Ohio, USA, 2006 [Google Scholar]
- J.F. Klapproth, M.L. Miller, D.E. Parker, Aerodynamic development and performance of the CF6-6/LM2500 compressor, in: American Institute of Aeronautics and Astronautics, 4th International Symposium on Air Breathing Engines, Orlando, FL, USA, 1979-7030 [Google Scholar]
- A.R. Wadia, D.P. Wolf, F.G. Haaser, Aerodynamic design and testing of an axial flow compressor with pressure ratio of 23.3:1 for the LM2500+ gas turbine, J. Turbomach. 124 (2002) 331–340 [CrossRef] [Google Scholar]
- R.O. Bullock, E.I. Prasse, Chapter 2 Compressor design requirements, in: I.A. Johnsen, R.O. Bullock (Eds.), Aerodynamic Design of Axial Flow Compressors, NASA SP-36, Washington D. C., USA 1965, pp. 9–51 [Google Scholar]
- S. Lieblein, F.C. Schwenk, R.L. Broderick, Diffusion Factor for estimating losses and limiting blade loadings in axial-flow-compressor blade elements, NACA RM E53D01, Washington D.C., 1953 [Google Scholar]
- J.D. Mattingly, W.H. Heiser, D.T. Pratt, Engine component design: combustion systems, in: J.S. Przemieniecki (Ed.), Aircraft Engine Design, 2nd edn., AIAA Education Series, AIAA, Reston, Virginia, USA, 2002, Chap. 9, pp. 325–418 [CrossRef] [Google Scholar]
- H.I.H. Saravanamuttoo, G.F.C. Rogers, H. Cohen, Axial flow compressors, in: Gas Turbine Theory, 5th edn., Dorling Kindersley (India) Pte. Ltd., Licensees of Pearson Education Ltd. in South Asia, New Delhi, India, 2001, Chap. 5, pp. 181–262 [Google Scholar]
- A. Pedersen, Ignition probability of a flammable mixture exposed to a gas turbine, MSc. thesis, Department of Energy and Process Engineering, NTNU, Trondheim, Norway, 2006 [Google Scholar]
- P.R. Holloway, G.L. Knight, C.C. Koch, S.J. Shaffer, Energy Efficient Engine High Pressure Compressor Detailed Design Report, NASA, Lewis Research Center, OH, 1982 [Google Scholar]
- Y.A. Cengel, Appendix 1 Property tables and charts (SI units), in: Introduction to Thermodynamics and Heat Transfer, 2nd edn., McGraw Hill, New York, USA, 2008, pp. 765–808 [Google Scholar]
- M.P. Boyce, Chapter 1 An overview of gas turbines, in: Gas Turbine Engineering Handbook, Butterworth-Heinemann, an imprint of Elsevier, Oxford, UK, 2012, pp. 3–87 [CrossRef] [Google Scholar]
- Y. Kashiwabara, Y. Matsuura, Y. Katoh, N. Hagiwara, T. Hattori, K. Tokunaga, Development of a high-pressure ratio axial flow compressor for a medium-size gas turbine, J. Turbomach. 108 (1986) 233–239 [CrossRef] [Google Scholar]
- I. Aartun, Using the program Allprops at the Center for Applied Thermodynamic Studies, University of Idaho, 2002. https://www.studentlitteratur.se/fileaccess/private/fid8263/ produkt/37354EnBe/torr_luft.pdf [Google Scholar]
- Forecast International, “www.forecastinternational.com,” November, 2010. www.forecastinternational.com/samples/F649_CompleteSample.pdf [Google Scholar]
- D. Bruna, C. Cravero, M.G. Turner, A. Merchant, An educational software suite for teaching design strategies for multistage axial flow compressors, J. Turbomach. 134 (2012) 051010-1 [CrossRef] [Google Scholar]
- S. Frei, ICAO Standard Atmosphere, Swiss Aviation Resources, 1997–2005. http://www.aviation.ch/tools-atmosphere.asp [Google Scholar]
- G.K. Serovy, R.P. Dring, Section 6.1 Test case E/CO-1 Single low speed compressor rotor, in: L. Fottner (Ed.), AGARD advisory report no. 275: Test cases for computation of internal flows in aero engine components, NATO AGARD Propulsion and Energetics Panel, Working Group 18, 1990, pp. 152–164 [Google Scholar]
- R.B. Ginder, D. Harris, Section 6.3 Test case E/CO-3 Single subsonic compressor stage, in: L. Fottner (Ed.), AGARD advisory report no. 275: Test cases for computation of internal flows in aero engine components, NATO AGARD Propulsion and Energetics Panel, Working Group 18, 1990, pp. 214–244 [Google Scholar]
- G.K. Serovy, R.P. Dring, Section 6.5 Test case E/CO-05 Low speed two stage compressor, in: L. Fottner (Ed.), AGARD advisory report no. 275: Test cases for computation of internal flows in aero engine components, NATO AGARD Propulsion and Energetics Panel, Working Group 18, 1990, pp. 286–298 [Google Scholar]
Cite this article as: F.H.A. Koh, Y.K.E. Ng, A one-dimensional stage un-stacking approach to reveal flow angles and speeds in a multistage axial compressor at the design operating point, Mechanics & Industry 20, 107 (2019)
All Tables
All Figures
 |
Fig. 1 Overview of the stage un-stacking method. Part 1. Thermodynamic model: Sections 2.10.1 and 2.10.2. Part 2. Axial variation model: Sections 2.2 and 2.10.3; Sections 2.3 and 2.10.4; Section 2.4; Sections 2.5 and 2.10.5. Part 3. Velocity triangle model: Sections 2.6 and 2.10.6. |
| In the text | |
 |
Fig. 2 Velocity diagram at the rotor inlet and rotor outlet. |
| In the text | |
 |
Fig. 3 Blockage models in this study. |
| In the text | |
 |
Fig. 4 The effect of flow turning angle in the IGV on the mean mismatch in flow angles per stage at each stator-outlet–rotor-inlet interface. |
| In the text | |
 |
Fig. 5 The effect of increasing v as a fraction of wheel speed at the OGV inlet on the mean mismatch in flow angles per stage at each stator-outlet–rotor-inlet interface. |
| In the text | |
 |
Fig. 6 Comparison of mean flow angle mismatch between pressure ratio models. |
| In the text | |
 |
Fig. 7 Maximum pressure ratios and used Pressure ratios with different pressure ratio model (stage outlets indicated by numbers in italics). |
| In the text | |
 |
Fig. 8 Stage axial velocity with different pressure ratio models (stage outlets indicated by numbers in italics). |
| In the text | |
 |
Fig. 9 Blade angles with different pressure ratio models. |
| In the text | |
 |
Fig. 10 Flow angles with different pressure ratio models. |
| In the text | |
 |
Fig. 11 Comparison of mean flow angle mismatch between SLC models. |
| In the text | |
 |
Fig. 12 Stage SLC distribution with different SLC models. |
| In the text | |
 |
Fig. 13 Specific stage static enthalpy rise with different SLC models. |
| In the text | |
 |
Fig. 14 Stage pressure ratios with different SLC models. |
| In the text | |
 |
Fig. 15 Stage axial velocity with different SLC models. |
| In the text | |
 |
Fig. 16 Pressure ratio distribution of selected gas turbines. |
| In the text | |
 |
Fig. 17 Estimated SLC distribution for the compressor in the LM 2500 gas turbine. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.