Open Access
Table B1
Asymptotic models.
| Models | Expression | Remark |
|---|---|---|
| Series |
|
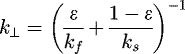
k
f
thermal conductivity fluid k s thermal conductivity solid Lower bound |
| Parallel |
|
k
f
thermal conductivity fluid k s thermal conductivity solid Upper bound |
| Maxwell lower bound [79] |
|
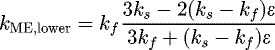
Solid medium with random distribution of small spheres |
| Maxwell upper bound [79] |
|
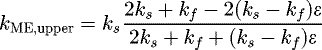
Solid medium with random distribution of small spheres. Dilute suspension |
| Bruggeman [80] |
|
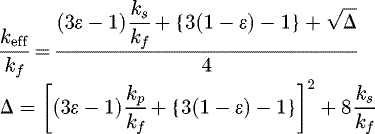
The main approach of this theory assumes that a composite material may be constructed incrementally by introducing infinitesimal changes to an already existing material |
| Hamilton-Crosser [28] |
|
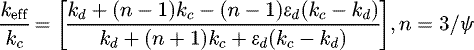
F: shape factor V: volume fraction |
| Maxwell, Comprehensive equation, from Hadley [81] |
|
Mixture of two material powders |
| Miller upper bound, |
|
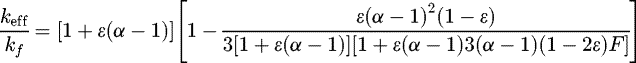
Symmetric cell material
 for spherical cell shape for plate cell shape |
| Miller lower bound, |
|
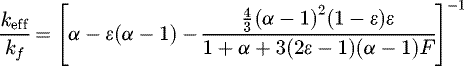
Symmetric cell material.
 for spherical cell shape for plate cell shape |
| Effective Medium Theory |
|
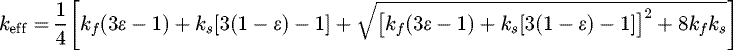
Developed from averaging the multiple values of the constituents that directly make up the composite material. |
| Hashin-Shtrikman [29] |
|
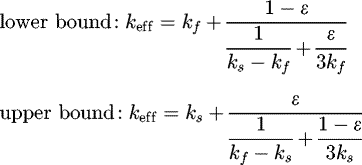
Variational theorems applied to the derivation of bounds for the effective thermal conductivity of macroscopically homogeneous and isotropic multiphase materials |
| Krischer [63] |
|
Packed bed of spheres. A highly anisotropic structure is assumed |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.