Open Access
Table B2
Analytical models.
| Researcher | Model | Remark |
|---|---|---|
| Behrang et al. [37] (Parallel-series-Maxwell model) |
|
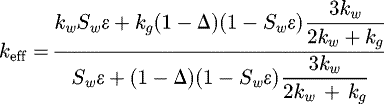
Sw
: wetting phase saturation K: thermal conductivity Δ: volume fraction ε: Porosity |
| Bhattacharya et al. [13] |
|
r: half thickness of fiber L: half-length of fiber |
| Yao et al. [82] |
|
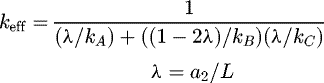
a2: geometrical parameter controlling cross-sectional size of ligament L: distance between centers of neighboring nodes |
| Gong et al. [83] |
|
In this theory, phases (or components) are treated as small spheres dispersing into an assumed uniform medium with the thermal conductivity km. m: uniform medium with dispersed spheres. e: two components system |
| Kou et al. [38] |
|
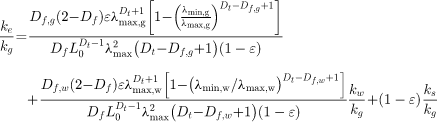
Fractal dimensions Df
, Dt
, and Df,w
(or Df,g
) ʎ: Pore size |
| Bhattacharya [84] circular lump corrected |
|
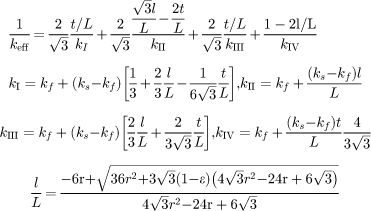
Developed for metal foams. 2D array of hexagonal cells, with hexagonal lumps of metal at fibers' intersection. Four layers in series |
| Boomsma and Poulikakos [32], revised |
|
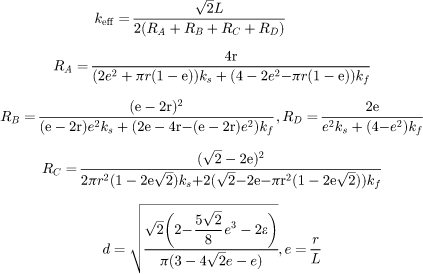
Developed for metal foams. 3D tetrakaidecahedron, struts of cylindrical cross section, with cubic nodes at fibres' intersection. Four layers in series. The parameter e must be estimated from data fitting. r: lump thickness L: strut length d: strut radius 
|
| Dai et al. [34] |
|
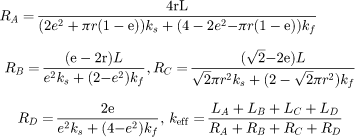
Developed for metal foams. Improvement of the above model. Accounts for struts' orientation Φ = 45∘ Good predictions but with an unfeasible value of e/r |
| Yang et al. [85] |
|
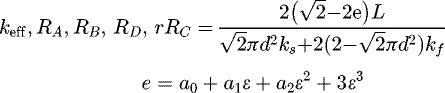
Developed for metal foams. Improvement of the acove model; considers the variation of e with porosity a0,a1,a2,a3 calibrated against data of [32]: valid for 0.905 < ε < 0.978 |
| Yang et al. [86] |
|
Developed for metal foams. 1/16th of a tetrakaidecahedron unit cell. No lumps at ligaments' intersection. The coefficient 1/3 is the reciprocal of thermal tortuosity. The same form of the Lemlich model is obtained |
| Yang et al. [11] |
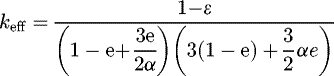 Accounting for the variation of struts'cross section:
|
1/16 th of a tetrakaidecahedron unit cell. Cubic nodes at ligaments' intersection. From experimental measurements on SEM images for Al foams: e = 0.3 and α = 1.5. α ≥ 1: node to ligament cross-sectional area ratio e ≥ 0: node thickness to strut length ratio φ: ratio of ligament cross-sectional area in the middle to that at the end |
| Kumar and Topin [87] |
|
Developed for metal foams. F is fraction of material oriented in heat flow direction |
| Kumar and Topin [87] PF model |
|
Developed for metal foams. Γ is defined as resistor model. Valid for 0.6 < ε < 0.95 |
| Dul'nev and Novikov [88] |
|
|
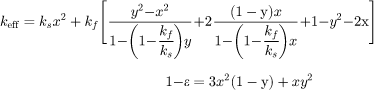
| Hsu et al. [89] touching square cylinders |
|
2 Dimensional l: length of one side of solid square cylinder |
| Hsu et al. [89] touching cubes |
|
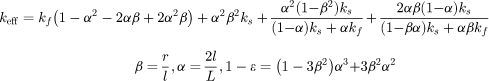
3 Dimensional l: length of one side of cube |
| Wang et al. [90] |
|
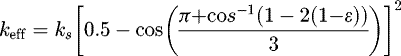
Efficient for all ranges of porosities and hollow or solid struts |
| Singh et al. [91] spherical inclusions |
|
n
': fractional volume of the more highly conducting phase a/b: node to cell size ratio |
| Singh et al. [91] cubic inclusions |
|
n
': fractional volume of the more highly conducting phase and a/b is node to cell size ratio C1 and C2: constants |
| Jagjiwanram and Singh [92] ellipsoidal inclusion |
|
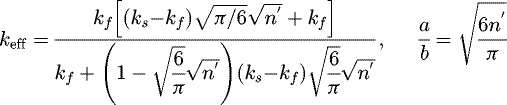
n ′: fractional volume of the more highly conducting phase and a/b is node to cell size ratio |
| Zehner and Schundler, from Ref. [36] |
|
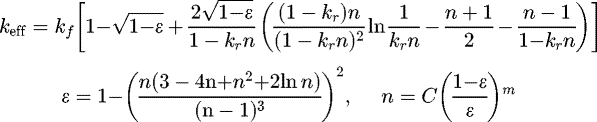
n is shape factor and at n = 1 solid becomes sphere k r = k f /k s : fluid/solid thermal conductivity ratio 
|
| Hsu et al. [36] Area contact model |
|
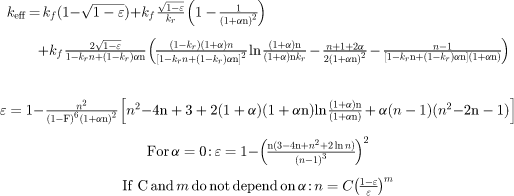
n is shape factor and at n = 1 solid becomes sphere k r = k f /k s : fluid/solid thermal conductivity ratio α: deformation factor |
| Hsu et al. [36] Phase-symmetry model |
|
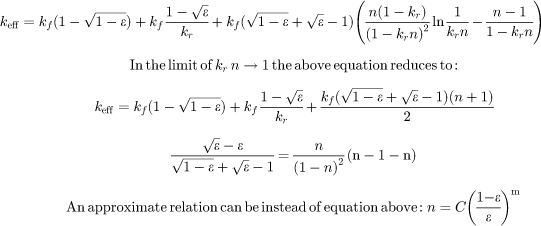
n is shape factor and at n = 1 solid becomes sphere k r = k f /k s : fluid/solid thermal conductivity ratio α: deformation factor |
| Russel, from Ref. [58] |
|
pores are cubes of the same size with solid walls of uniform thickness |
| Ahern et al. [93] |
|
 : the fraction of solid material contained in the windows and β declares strut shapes : β = 1/3 for cylindrical struts and β = 2/3 for the plate-like windows |
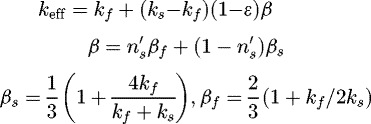
| Schuetz and Glicksmann, from Ref. [93] |
|
β = 1/3 for cylindrical struts and β = 2/3 for the plate-like windows |
| Fiedler et al. [94] |
|
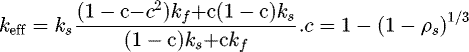
Determining ETC based on relative density of solid |
| Singh et al. [95] |
|
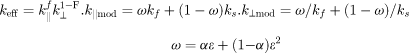
In order to take into accouter the random distribution of cells in the continuous matrix as well as the wide difference in the thermal conductivity of the constituents, a non-linear second-order correction term is correlated |
| Donea Variational Model from Ref. [96] |
|
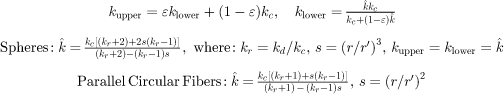
r: radius of inclusion, r ':radius of the largest possible spherical shell surrounding the inc!iision for random dispersion of spheres |
| Bauer [97] |
|
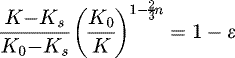
Compatible with experimental data obtained from wide range of thermal conductivity, pore shape and distribution k0: thermal conductivity of unperturbed continuous medium |
| Kuwahara et al. [98] |
|
Analytical correlation established for air and aluminium as fluid and sold phases under non-equilibrum thermal condition |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.