Open Access
Table B4
Unit cell models ETCs of open-cell metal foams.
| Researcher | Unit cell | Correlation | Remarks |
|---|---|---|---|
| Calmidi and Mahajan [33] |
|
|
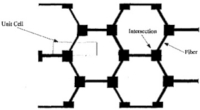
Two-dimensional hexagonal array square nodes fibers are the edges of the hexagons one dimensional conduction : ligament to node size ratio representative unit cell:
Divided into three layers in series formation and parallel law is would be applied for each separate layer |
| Bhattacharyaet al. [13] |
|
|
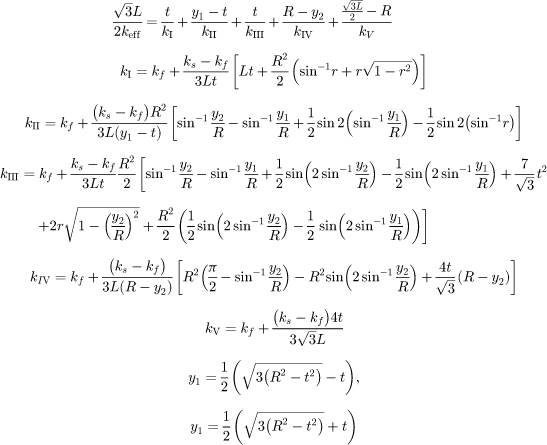
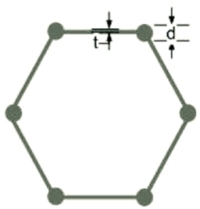
–Six-fold rotational symmetry –Circular cross sction representative unit cell: 
Divided into 5 layers in series and in each layer fluid and solid phases would be in parallel formation. R: radius of circular intersection |
| Du Plessis and Fourie [110] |
|
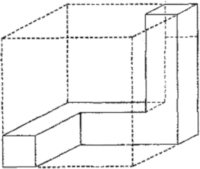
Representative unit cell was used to study hydrodynamic features of cellular structures. | Three joint square ducts each square oriented perpendicularly to the other two sections are required to exhibit maximum possible interconnectivity. |
| Dulnev [111] |
|
|
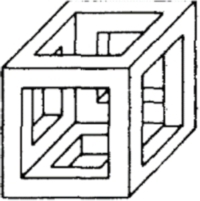
L: outside diamension of the unit cell Also was used to examine Odelovski correlation |
| Boomsma and Poulikakos [32] |
|
|
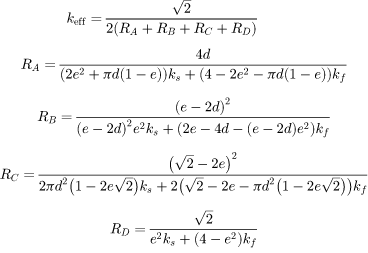
The tetrakaidecahedron modeled with cylindrical ligaments and cubic nodes. d: dimensionless foam ligaments radius e: dimensionless cubic node length representative unit cell 
|
| Schimierer and Razani [69] |
|
|
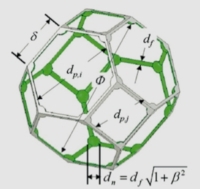
Three-dimensional geometric model of open celled Doucell foam Spherical nodes with the TetraK model ligament cross section is circular and the diameter is constant over its length kst: thermal conductivity of 304 stainless steel Ac: cross sectional area L: length between thermocouple locations 5 thermocouple were used (1,2,3,4,5) |
| Ozmat et al. [112] |
|
NA | Structure of metal foam and dodecahedron having 12 pentagon-shaped facets |
| Krishnan et al. [113] |
|
Body center cubic Face center cubic A15 arrangement ETC was calculated numerically by solving conduction heat transfer |
Unit cell geometries were obtained by substracting the cell cube from spheres at various lattice points Convex triangular ligaments cross sectional area Symmetric tetrahedral nodes |
| Rayleigh models from [114] |
|
|
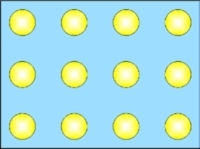
Spherical particles arranged in simple cubic array embedded in a continuous matrix |
| Rayleigh models from [114] |
|
|
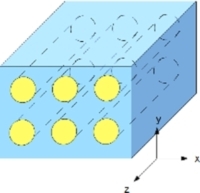
Consisting of parallel cylinders embedded in a continuous matrix Assuming z is the axis parallel to the fibers |
| Percolation model [114] |
|
High-conductivity particles are depicted as black. White is for low-conductivity particles | |
| Yang et al. [86] |
|
|
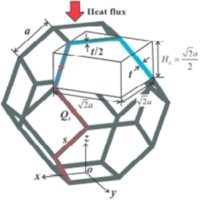
An open-cell Al foam modeled with a tetrakaidecahedron unit cell having a uniform thickness of square ligaments |
| Yang et al. [11] |
|
 Accounting for the variation of struts 'cross section:
|
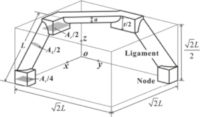
1/16th of a tetrakaidecahedron unit cell. Cubic nodes at ligaments' intersection. From experimental measurements on SEM images for Al foams: e = 0.3 and α = 1.5. α ≥ 1: node to ligament cross-sectional area ratio Page 37 of 77 e ≥ 0: node thickness to strut length ratio h: ratio of ligament cross-sectional area in the middle to end |
| Haghighi and Kasiri [44] |
|
|
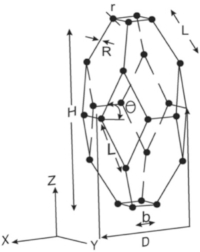
Unit cell is discretized to five parallel layers in the y direction The ligaments of all quadrilateral faces are laid between two adjacent cells Each node at the fiber intersections is common between two cellsk is the summation of the effective thermal conductivity of each layer in series L: ligament length Θ: The inclination angle that defines the orientation of the hexagonal faces with respect to the rise direction l: Length of the sides of horizontal square faces e: Dimensionless spherical node diameter |
| Talukar et al [115] |
|
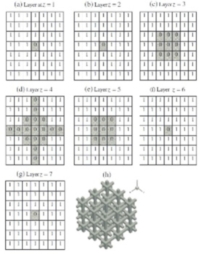
A Cartesian coordinate based finite volume method (FVM) has been used for solving the combined conduction-radiation problem inside porous media. porosity is uniform within the porous matrix the thermo-physical properties of the solid as well as the fluid (participating media) in the pores are constant over the range of temperature encountered in the simulation, |
These porous structures have been assumed to be regularly repeating in all the three directions The representative computational domain of the porous medium has been divided into a number of control volumes (CVs); each of which can be designated either as the solid or the fluid (void) control volume |
| Yao et al. [82] |
|
|
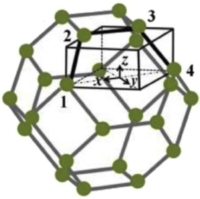
a1: geometrical parameter controlling cross-sectional shape of ligament a2 geometrical parameter controlling cross-sectional size of ligament L: ligament length |
| Edouardo [45,46] |
|
|
Consist of 12 cylindrical ligaments and 8 cubic nodes 2b: strut diameter and 2x: cubic node length |
| Huu et al. [47] |
|
NA | - |
| Cubic cell lattice [48–50] |
|
NA | Cell size is equal to cubic lattices |
| Yu et al. [116] |
|
|
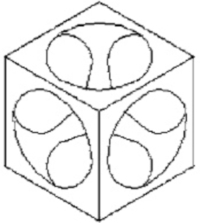
Cubic unit cell model for porous carbon foam t: is the normalized thickness of the square bar |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.