| Issue |
Mechanics & Industry
Volume 18, Number 4, 2017
|
|
|---|---|---|
| Article Number | 414 | |
| Number of page(s) | 22 | |
| DOI | https://doi.org/10.1051/meca/2017012 | |
| Published online | 28 August 2017 | |
Regular Article
Stiffness and energy dissipation of Oval Leaf Spring mounts under unidirectional line loading
1 National Center of Applied Research in Earthquake Engineering, Algiers, Algeria
2 National School of Built and Ground Works Engineering, Algiers, Algeria
3 Department of Civil & Environmental Engineering, College of Engineering, University of Sharjah, Sharjah, United Arab Emirates
4 Department of Civil Engineering, Houari Boumedien University of Science & Technology, Algiers, Algeria
⁎ e-mail: benyoucefenstp@gmail.com
Received:
10
July
2016
Accepted:
3
February
2017
The Oval Leaf Springs (OLS), a class of passive isolation devices, have been successfully used as anti-shock and anti-vibration mounts to protect equipment and machinery. Available literature is insufficient to understand the behavior of OLS mounts. To estimate the spring stiffness, we conducted theoretical and finite element analyses (FEA) on a large number of springs having different geometrical and mechanical properties. Based on the principle of minimum potential energy, this paper presents theoretical expressions, which describe the linear static stiffness of OLS mounts subjected to line loading in the vertical (compression) and lateral (bending–shear) in-plane directions. Comparison studies showed a good agreement between numerical and analytical models. We observed a negligible effect of transverse shearing on the spring stiffness. In addition, it was demonstrated that the stiffness is more sensitive to the radius compared to the other geometric properties of the spring. Nonlinear FEA considering the hyper-viscoelastic behavior of the damping compound showed that the OLS mounts have higher energy dissipation capabilities in the lateral direction, which increase at low frequency and large amplitude loadings.
Key words: Oval Leaf Spring / stiffness / damping / finite element analysis / hyper-viscoelastic / energy dissipation / frequency
© AFM, EDP Sciences 2017
1 Introduction
In engineering, vibration is one of the main factors that need to be considered while designing equipment or structures. The sources of vibration can be either natural such as earthquakes and winds or man-made such as operation of heavy machinery and construction works. In many practical situations, vibrations are unavoidable, but should be within tolerable limits. During ground motions or operation of heavy machinery, vibrations may reach unacceptable levels and result in structural damage and equipment failure. Hence, adding an isolation system to suppress these vibrations becomes necessary. There are two types of isolation systems that are currently employed, namely, active and passive systems. An active system can suppress the vibration better than a passive system, however, it requires external power supply and feedback circuit to control the vibration attenuation process. Passive devices are mechanical assemblies made of different materials and designed to improve damping, stiffness, and strength of structures [1]. Contrary to actively controlled systems; passive energy dissipation devices can easily be replaced without compromising the structural integrity since they are not part of the main structure [2]. In addition, active isolation systems are design-intensive and expensive. On the other hand, a passive isolation system does not need external supply, requires easier design, and inexpensive. As a result, passive systems are the most preferred in industrial and automobile applications, such as the Oval Leaf Spring (OLS) mount shown in Figure 1.
The OLS is formed using two or more high-tensile stainless steel U-shaped leaves, joined together in the center portion with face-plates with a circular shape. The steel leaves provide the needed flexibility while the compound material enhances the damping capacity. Earlier, the Elliptical Leaf Spring, ELS (a variant of leaf spring mounts with an elliptically shaped face-plates) mountings were specifically designed for shipboard applications and were particularly suitable to protect marine equipment from shock due to underwater explosions. Later, the use of ELS mounts has been extended to isolate heavy machinery, air compressors, engine suspensions, and sensitive equipment. Features of the ELS mounts include the effective operation at low natural frequency and ability to attenuate large shock inputs [3].
In general, the OLS mount is a mechanical device that absorbs the vibrational energy by undergoing deformation and then release it. Hence, the strain energy of the material and the shape become a major factor in designing the springs [4,5]. The “U” shape of the ELS leaves possess the ability to act as spring and have been used in other vibration isolation devices. The behavior of “U” shaped leaves has been the subject of few studies [6–11]. Kishiki et al. [6] conducted an experimental evaluation of cyclic deformation capacity of U-shaped steel dampers for base-isolated structures. Kwon et al. [7] performed an analytical study on the shape development of U-shaped steel damper for seismic isolation system. Oh et al. [10,11] performed experimental and analytical studies on U-shaped hysteresis dampers. They reported that “U” shaped dampers could be used as energy-dissipating devices for base isolating systems since they can sustain large displacements without strength and stiffness degradation.
Tse and Lung [9] carried out finite element analysis and theoretical study on the large deflections of composite circular springs and validated their results by experiments under uniaxial tension. The authors found that the spring stiffness increased with deflection and hard spring behavior was showed throughout the whole range of applied loads. The shear and longitudinal deformations effects were found to be negligible for configurations in which the elastic modulus to shear modulus ratios were not large and the radius to thickness ratios were large. In another study, Tse et al. [8] considered the case of composite circular springs with extended flat contact surfaces and carried out finite element analysis and theoretical study on the new spring stiffness under unidirectional line loading and surface loading configurations. The authors showed that the spring stiffness increases with the increase in width and thickness of the composite spring but decreases with the increase in inner radius. However, the spring stiffnesses were more sensitive to the change in spring radius than the thickness. As an extension to the studies conducted previously by Tse et al. [8,9], Wong et al. [12] demonstrated that the reduction in spring stiffness at elevated temperatures could be prevented by the embedment of nickel-titanium alloy wire as a compound.
Several studies dealt with damping compounds and proposed the use of viscoelastic materials. For instance, Treviso et al. [13] presented a review of properties and models of damping in composite materials. Their study reported that for the damping purposes, employing a soft, viscoelastic material is preferred for the core while metals can be used for the skins. Ganapathi et al. [14] carried out a numerical study of sandwich and laminated composite beams using linear and nonlinear dynamic analysis, they used a viscoelastic material as a core to enhance their damping capacity. The results of the analyses demonstrated that increasing the core thickness enhances the damping significantly. Hao and Rao [15] reported that viscoelastic layered systems can provide a simple and flexible solution for damping vibration of sheet metal panels. They developed an analytical formulation to predict the stiffness and damping of three-layered beams with two different viscoelastic materials adjacent to each other.
Verbaan et al. [16] demonstrated the advantage of applying viscoelastic materials instead of purely viscous materials as damping medium in mechanical dampers. However, they found that at high frequencies, the stiffness increases and the damping capacity decrease significantly. This is in line with the findings of De Lima et al. [17] who conducted a time-domain modeling procedure of structures containing both viscoelastic materials and shape memory alloys (SMA) wires for vibration mitigation. The study concluded that as the excitation frequency increases, the hysteresis loop area decreases significantly, which can affect significantly the damping capability of the SMA wires. For wider frequency applications, Xu et al. [18] designed a vibration isolation device based on viscoelastic materials, which was deemed suitable for vibration suppression under wide frequency excitation. A review on the vibration damping materials like rubbers, polymers, metals, metal-matrix composites and smart materials in terms of damping capacity, stiffness, mechanical strength and figure of merit can be found in Choudhary and Kaur [19].
The main objectives of this investigation are to develop analytical solutions to the linear static stiffness and to assess the energy dissipation capabilities of OLS mounts in the vertical (compression/tension) and horizontal (bending–shear) in-plane directions. First, a series of three-dimensional linear FEA is performed to validate the analytical solutions and to investigate the effect of different properties on the in-plane spring static stiffness. Then, a nonlinear, large deflection, FEA study is conducted to characterize the effective stiffness and to assess the energy dissipation capabilities of four mounts, assuming the nonlinearity of the steel face-plates and the hyper-viscoelasticity of the damping compound [13].
 |
Fig. 1 The Oval Leaf Spring (OLS). |
2 Theoretical analysis
The strain energy expression for a curved beam is a special reduced form of that for a thin shell [20]. The relative importance of strain energy UM in bending and US in shear loading of beams is influenced by the ratio of the length L, the radius R of the spring to its thickness t (Fig. 2), by the shape of the cross section and by the type of loading. The relative magnitude of UM and US are examined in [21] for a given set of ratios of L/t, R/t, and given cross section. However, more accurate solutions and experimental data indicate that the strain energy due to bending UM is fairly accurate, except for relatively short beams. If the ratio of the radius of curvature to the thickness of spring is less than 5, the flexure formula is generally inadequate for describing the flexural stresses in the spring.
In this study, we assume that the dimension R and L are large compared to the spring thickness, t. Many curved members, such as closed rings and chain links, are statically indeterminate. The additional relations needed to solve for the loads are obtained using Castigliano's theorem with appropriate boundary conditions [21]. In calculating the displacement using Castigliano's theorem and strain energy, we are supposing that the stress is linearly distributed along the section of the spring [22]. This assumption is often made and found to be reasonable in non-circular rings where bending is the predominant mechanism of deformation. In order to establish the analytical solution, the energetic approach is used to determine the stiffnesses of the OLS mount.
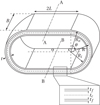 |
Fig. 2 OLS geometric properties. |
2.1 Geometry description of OLS mount
Figure 2 illustrates the OLS mount considered in this study. The spring consists of two flat surfaces on top and bottom with length 2L and two circular portions with mean radius R, outer radius Ro, and inner radius Ri from center C. The spring has a width B and an overall thickness t, t = tc + 2tf, tf = 1.27 mm (0.05 in.), with tf being the thickness of the face-plate. The 2D spring shows symmetry in the x − y plane with the origin of x − y coordinate system located at the center of the spring O. The advantage of this type of spring geometry is the constant value of the spring's radius of curvature in the unstrained state, whereas in the non-circular springs (such as the elliptical leaf spring) the curvature of the spring varies at each point along the spring length, and the complexity of their analysis comes from the fact that the end torque is a function of these variable coefficients [23].
2.2 Boundary conditions and loading
The OLS is subjected to a line-loading at the centerline A–A of the flat contact surface at the top while the centerline B–B at the flat contact surface at the bottom is fixed. There are three cases of external force loading that are of interest: (1) vertical in-plane loading in y-direction, (2) horizontal in-plane loading in x-direction, and (3) out-of-plane loading in z-direction. However, in this study, we focus on the in-plane loading since the OLS is designed to operate in its plane.
2.3 Analytical solution of the static stiffness
In the development of the analytical solution to the OLS stiffness, we describe the compound's elastic modulus, Ec, as a fraction, nE, of the facing's elastic modulus, Ef (i.e., nE = Ec/Ef). In this section, we derive the in-plane vertical compressive stiffness ky and the in-plane bending–shear stiffness kxy of the spring.
2.3.1 Effective engineering properties
In this section we determine, through the classical laminate theory, the effective flexural stiffness, EIeff, and the effective axial stiffness, EAeff, which are needed to determine the stiffness of OLS mounts in the vertical and horizontal in-plane directions.
For an isotropic linear elastic material, the plane stress relationship between the Cartesian stresses and strains is: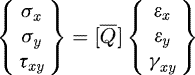 (1)where
(1)where 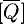 is the stiffness matrix. Each lamina (face-plates and compound core) has a different
is the stiffness matrix. Each lamina (face-plates and compound core) has a different 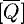 . For instance, the stiffness matrix for the face-plate is given by:
. For instance, the stiffness matrix for the face-plate is given by: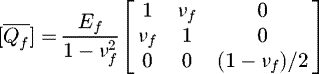 (2)and for the compound is:
(2)and for the compound is: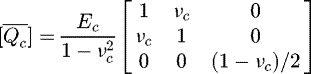 (3)where νf and νc are the material's Poisson's ratio of the face-plates and the compound, respectively. As we will see later, the Poisson's ratio has a negligible effect on the global behavior of the OLS mounts, hence, we consider νf = νc = ν.
(3)where νf and νc are the material's Poisson's ratio of the face-plates and the compound, respectively. As we will see later, the Poisson's ratio has a negligible effect on the global behavior of the OLS mounts, hence, we consider νf = νc = ν.
The laminate extensional, Aij, and bending, Dij, stiffness matrices are given by: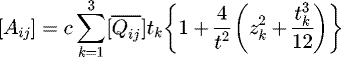 (4)and
(4)and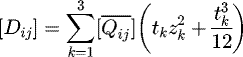 (5)where c is the shear correction factor, which is equal to 6/5 for a rectangular section. tk and zk are the thickness and location of the centroid (from the mid-plane) of the kth lamina, respectively.
(5)where c is the shear correction factor, which is equal to 6/5 for a rectangular section. tk and zk are the thickness and location of the centroid (from the mid-plane) of the kth lamina, respectively.
Using the above matrices we can define the effective engineering properties of the laminate, namely, the effective flexural stiffness, EIeff, and the effective axial stiffness, EAeff. These are given by [8]: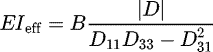 (6)and
(6)and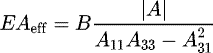 (7)where |D| and |A| are the determinants of the bending and extensional stiffness matrices of the laminate. Substituting equation (4) into equation (6) and equation (5) into equation (7) yields:
(7)where |D| and |A| are the determinants of the bending and extensional stiffness matrices of the laminate. Substituting equation (4) into equation (6) and equation (5) into equation (7) yields: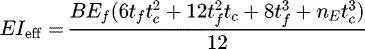 (8)
(8)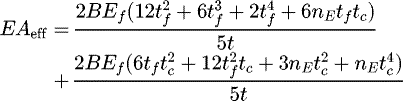 (9)
(9)
2.3.2 In-plane vertical compressive stiffness, ky
The OLS is subjected to the unidirectional compression line load F in the y-direction as shown in Figure 3(a). Due to symmetry, only one quadrant of the spring (Fig. 3(b)) needs to be considered, with a force reduced to (F/2) acting on the section A–A. The bending moment M0 acting on this section is statically indeterminate, hence, we shall use Castigliano's theorem to find it, knowing that from the condition of symmetry the cross section A–A does not rotate during the bending moment of the spring.
The strain energy expression for the complete OLS mount derived from the quadrant model is: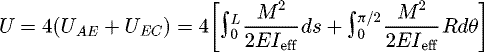 (10)where UAE and UEC are the strain energy in the two portions AE and EC, respectively. M and EIeff are the bending moment and the effective flexural stiffness at any cross section of the spring, s is the distance from section A to section E in the x-direction and θ is the angular coordinate from section E to section C. The effective flexural stiffness at any cross section is given by equation (8). By substituting the moment resultants into equation (10) we get:
(10)where UAE and UEC are the strain energy in the two portions AE and EC, respectively. M and EIeff are the bending moment and the effective flexural stiffness at any cross section of the spring, s is the distance from section A to section E in the x-direction and θ is the angular coordinate from section E to section C. The effective flexural stiffness at any cross section is given by equation (8). By substituting the moment resultants into equation (10) we get: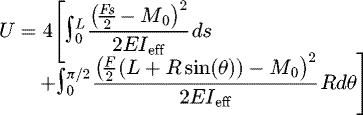 (11)
(11)
Realizing that the displacement corresponding to M0 is zero (i.e., dU/dM0 = 0), we can calculate M0 as: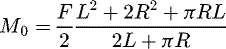 (12)
(12)
Substituting into equation (11) and using Castigliano's second theorem, the displacement in y-direction is obtained as: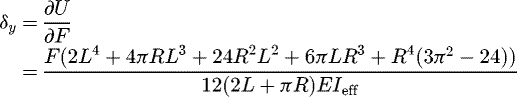 (13)and the in-plane compression spring stiffness is:
(13)and the in-plane compression spring stiffness is: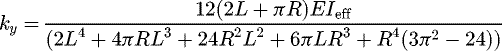 (14)
(14)
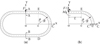 |
Fig. 3 OLS subjected to vertical compressive load. |
2.3.3 In-plane bending–shear stiffness, kxy
The OLS is subjected to the unidirectional line load F in the x-direction at point A as shown in Figure 4(a). Due to symmetry only one half of the spring (Fig. 4(b)) needs to be considered, with the force reduced to F/2 acting on section A–A. The bending moment at this section would vanish according to the principle of least work. The indeterminate shear force Q shall be determined using Castigliano's theorem.
The strain energy due to the bending moment, UM, and the tensile influence of the force F, UN, is expressed as: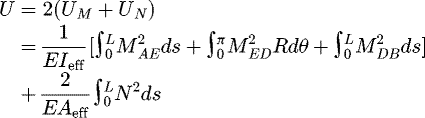 (15)where MAE, MED, MDB are the bending moments at any section from section A to section E, from section E to section D, and from section D to section B, respectively. N(N =− F/2) is the in-plane normal force. The axial stiffness, EAeff, at any cross section is given by equation (9).
(15)where MAE, MED, MDB are the bending moments at any section from section A to section E, from section E to section D, and from section D to section B, respectively. N(N =− F/2) is the in-plane normal force. The axial stiffness, EAeff, at any cross section is given by equation (9).
Knowing that the tangential displacement at section A–A is zero (i.e., dU/dQ = 0), we can calculate Q as: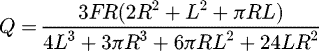 (16)
(16)
Substituting into equation (15) and using Castigliano's second theorem, the displacement in x-direction is obtained as: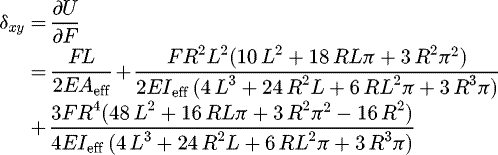 (17)and the in-plane bending–shear spring stiffness is:
(17)and the in-plane bending–shear spring stiffness is: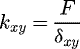 (18)
(18)
 |
Fig. 4 OLS subjected to bending–shear load. |
3 Linear static behavior
To consider the transverse shearing effects that were not included in the theoretical analysis, the ANSYS finite element package (version 16.0) was used to evaluate the stiffnesses of the OLS mount. The three-dimensional SOLID95 element was selected to model the Oval Leaf Spring. The SOLID95 element defined by 20 nodes having 3 degrees of freedom per node can tolerate irregular shapes and is capable to model curved boundaries. Full model was considered in this study. The automatic meshing capability of the package meshed all models. Linear analysis was employed for this study. Table 1 summarizes the geometric properties of the OLS mounts considered in this study, where every spring is constructed using any of the possible combinations of these properties. The antivibration mounts are made of stainless steel facing (Ef = 200 GPa, νf = 0.3). The outer and inner U shaped facings, having constant thickness tf = 1.27 mm (0.05 in.), are riveted together at the open ends with face-plates to form an oval shaped assembly. The space between the stainless steel facings is filled with a damping compound (Ec = nE Ef). The elastic modulus of the compound material is varied to cover a wide range of possible fillings: from Ec = 0.05Ef until Ec = Ef. Poisson's ratio of the compound material is found to have negligible effect on the deflections of the spring, thus, it is kept constant at νc = νf.
To verify the accuracy of the theoretical results obtained in the previous section, finite element analyses were performed on all springs. Then the variations of the two stiffnesses, ky and kxy, with the spring's thickness, radius, width, length, and compound material properties were determined. All nodes along the line B–B at the bottom were fixed. For the vertical in-plane load case (i.e., compression), nodes along the line A–A at the top were subjected to a vertical compression line-loading and were constrained in the other directions. For the horizontal in-plane load case (i.e., bending–shear), nodes along the line A–A were subjected to a line loading in the x-direction and were constrained to move in the other directions.
Geometric properties of the OLS mounts.
3.1 OLS without compound (Ec = Ef)
Table 2 summarizes the numerical and theoretical stiffnesses obtained for different values of total thickness t. Note that at this point there is no compound (i.e., Ec = Ef). It can be observed that there is a good agreement between the stiffnesses calculated using the developed equations (Eqs. (14) and (18)) and those obtained using finite element analysis. Small discrepancies between the theoretical and finite element analysis results are noted only at relatively high stiffness. Hence, the transverse shearing effect is insignificant in these cases as far as the current investigation is concerned. From Table 2, we observe that the OLS mounts are flexible in the horizontal in-plane direction and stiffer in the vertical direction.
Inner radii of 1.5 times smaller or bigger than 50 mm (i.e., 38 mm and 85 mm) were also used in the current investigation in order to study the size effect on spring stiffnesses. Within the boundaries of variation in R and t in the current investigation, it can be observed from Figure 5 that an increase in the spring thickness would not be an effective way to increase the stiffness of OLS with large inner radius (i.e., in the range between 85 and 100 mm). The effectiveness of increasing stiffness by means of increasing the thickness was more pronounced for the OLS mounts with relatively small inner radii (i.e., in the range between 38 and 50 mm). Furthermore, the stiffness increases as the radius decreases and it is more sensitive to the change in OLS radius than its thickness. From the theoretical expressions of ky and kxy, it is clear that the stiffness is inversely proportional to the cubic of radius R.
Variation of the stiffness with thickness and width are depicted in Figure 6. It can be seen that all the spring stiffnesses are highly dependent on the thickness and width. In other words, one of the most effective ways to adjust the OLS stiffness at low radius and length (when R/t and L/t are close to 5) is to alter the thickness or the width. Furthermore, the theoretical solution (Eqs. (14) and (18)) predicts that ky and kxy are linearly proportional to the width B of the OLS and cubically proportional to the thickness t.
As shown in Figure 6(b), all curves have a similar trend (for ky and kxy); the stiffness in all directions increases significantly with the increase in thickness. Figure 6(a) shows the influence of width on the OLS stiffnesses. With a constant length, radius, and thickness, the spring stiffnesses ky and kxy increase linearly with the spring width.
Comparison of numerical and theoretical stiffness of OLS mounts with Ec = Ef.
 |
Fig. 5 Variation of the OLS stiffness with thickness and radius (Ec = Ef). |
 |
Fig. 6 Variation of the OLS stiffness with thickness and width (Ec = Ef). |
3.2 OLS with compound (Ec ≠ Ef)
Tables 3 and 4 compare the theoretical and numerical results obtained for a selected number of springs. Again, we observe a good agreement between the two solutions. Results of the finite element analyses performed on the springs with different material and geometric properties are plotted in Figures 7–10.
Comparison of numerical and theoretical stiffness of OLS mounts with Ec = 0.05Ef.
Comparison of numerical and theoretical stiffness of OLS mounts with Ec = 0.1Ef.
 |
Fig. 7 Variation of the average normalized stiffness with t and nE. |
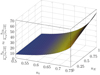 |
Fig. 8 Variation of the average normalized stiffness with nt and nE. |
 |
Fig. 9 Variation of the average normalized stiffness with R and L. |
 |
Fig. 10 Variation of the average normalized stiffness with L and R. |
3.2.1 Effect of compound's elastic modulus (Ec)
Figure 7 shows the variation of the average normalized spring stiffnesses ky/ky(Ec = Ef) and kxy/kxy(Ec = Ef) with nE. It is clear that the normalized stiffnesses increase linearly with the compound material elastic modulus, Ec, and this variation can easily be demonstrated to be independent of the spring width, B, face-plate length, L, and radius, R. Both ky and kxy are more sensitive to Ec for thick springs. Analytically, the normalized stiffnesses can be calculated to be: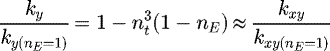 (19)where nt = tc/t is the core to total spring thickness ratio. Equation (19) can be used to calculate the stiffness based on the stiffness of the same spring with one material (Ec = Ef = E).
(19)where nt = tc/t is the core to total spring thickness ratio. Equation (19) can be used to calculate the stiffness based on the stiffness of the same spring with one material (Ec = Ef = E).
3.2.2 Effect of compound's thickness (tc)
Figure 8 shows the variation of the normalized stiffness ky/ky(nt = 0) and kxy/kxy(nt = 0) with the variation of the core to total thickness ratio, nt = tc/t. It is clear that nt has a considerable effect on the variation of the normalized stiffness; an increase in nt increases significantly the normalized stiffness of the spring in all directions, especially for high values of nE. Analytically, the normalized stiffness can be calculated to be: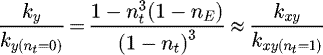 (20)
(20)
3.2.3 Effect of the spring radius (R)
Figure 9 plots the variation of the normalized stiffness ky/ky(R = 38 mm) and kxy/kxy(R = 38 mm) with the spring radius, R, for different face-plate lengths. It is observed that an increase in the radius decreases considerably the spring compressive stiffness, especially for short face-plate lengths, L. An increase in the radius induces a cubic decrease of the spring stiffnesses ky and kxy. This confirms the analytical solutions presented in equations (14) and (18). In addition, the effect of increased R in reducing the compressive stiffness, ky, is more pronounced for short faceplate lengths. However, the effect of L on the normalized bending–shear stiffness, kxy, is insignificant compared to R.
3.2.4 Effect of the spring length (L)
To study the effect of spring length on the stiffnesses, the length L of the face-plate (total face-plate length is 2L) was varied to cover a wide range of practical OLS mounts and the stiffness was recorded for each spring length, the results are reported in Figure 10. It is clear that the OLS stiffness is highly dependent on the length of the flat surface. An increase in L reduces considerably the spring stiffnesses, this influence is more pronounced for smaller values of R.
3.2.5 Effect of the spring width (B)
From equations (14) and (18) it is clear that the compressive stiffness and bending–shear stiffness increase linearly with the increase in spring width, B.
3.3 Relationship between the compressive stiffness and bending–shear stiffness
To investigate the relationship between the spring compressive stiffness, ky, and bending–shear stiffness, kxy, the ratio φ = ky/kxy is calculated for all OLS mounts constructed based on all possible combinations of the geometric properties shown in Table 1. Table 5 summarizes the average ratio, φavg, with the corresponding values of L and R. The standard deviation, σφ, is provided to measure how widely the φ values are dispersed from φavg. Interestingly, the φ ratio is almost independent of all spring properties except L and R.
From the analytical stiffness expressions (Eqs. (14) and (18)) we can calculate the sensitivities of φ to the variation of B, t, tf, and nE, by computing the derivative of φ with respect to each of these parameters. The obtained derivatives are almost equal to zero, indicating that the φ ratio is insensitive to the variation of these parameters.
Numerical and theoretical 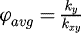 ratio.
ratio.
3.4 The special case of very soft compounds
In the special case of very soft compounds such as elastomers, which are characterized by a negligible elastic modulus compared to the face-plates material (i.e., stainless steel), the theoretical formulas for the stiffness in the vertical (Eq. (14)) and in the lateral (Eq. (18)) directions need to be modified to provide accurate estimations. For this reason, several OLS mounts with different geometric and compound material properties were analyzed using ANSYS and the obtained static stiffness, in each direction, was compared to the stiffness calculated using the proposed analytical formulas with nE = 1. Next, a multivariate nonlinear regression analysis was used to fit the ratios 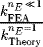 to the following equation:
to the following equation: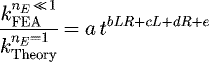 (21)in which a, b, c, d, e are fitting constants to be determined for each loading direction. For the stiffness ratio in the vertical direction a = 2.451, b = 5.08 × 10−6, c = 2.06 × 10−3, d = 3.28 × 10−3, e = 2.8377, and in the lateral direction a = 2.987, b =−16.5 × 10−6, c = 4.45 × 10−3, d = 7.17 × 10−3, e =−2.8365. Therefore, the vertical stiffness,
(21)in which a, b, c, d, e are fitting constants to be determined for each loading direction. For the stiffness ratio in the vertical direction a = 2.451, b = 5.08 × 10−6, c = 2.06 × 10−3, d = 3.28 × 10−3, e = 2.8377, and in the lateral direction a = 2.987, b =−16.5 × 10−6, c = 4.45 × 10−3, d = 7.17 × 10−3, e =−2.8365. Therefore, the vertical stiffness, 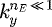 , of an OLS mount with a very soft damping compound is determined based on the vertical stiffness calculated using equation (14) with nE = 1,
, of an OLS mount with a very soft damping compound is determined based on the vertical stiffness calculated using equation (14) with nE = 1, 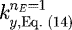 , that is:
, that is: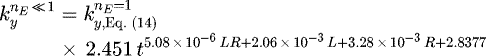 (22)similarly, the stiffness in the lateral direction,
(22)similarly, the stiffness in the lateral direction, 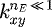 , is calculated based on equation (18) with as follows:
, is calculated based on equation (18) with as follows: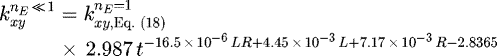 (23)
(23)
Figure 11 compares the vertical and lateral stiffness ratios 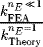 to the ratios obtained using equations (22) and (23), respectively. Clearly, a good agreement is seen between both results. Note, that the OLS mount width, B, was found to have an insignificant influence on both stiffness ratios.
to the ratios obtained using equations (22) and (23), respectively. Clearly, a good agreement is seen between both results. Note, that the OLS mount width, B, was found to have an insignificant influence on both stiffness ratios.
 |
Fig. 11 Comparison of OLSs stiffness ratios. |
4 Nonlinear cyclic behavior
In this section, the cyclic behavior of OLS mounts is investigated assuming material and geometric nonlinearities. For this purpose, a series of three-dimensional nonlinear finite element analysis (NLFEA) were carried out on four mounts (Tab. 6) using ANSYS. The hysteretic behavior and energy dissipation of each mount are assessed assuming the two loading cases: compression/tension (vertical direction) and bending–shear (lateral direction).
Geometry of OLS mounts considered in the NLFEA.
4.1 Finite element modeling
Both material and geometric nonlinearities with large deformation have been considered. All parts of the mounts were modeled using SOLID186 elements (Fig. 12). SOLID186 element is a higher-order 3D node element that exhibits quadratic displacement behavior and supports plastic, hyperelastic, and large deformation capabilities. The automatic meshing capability offered by ANSYS was employed. The boundary conditions and load application regions are as shown in Figure 12.
To assess their cyclic behavior in the compression/tension direction, the OLS mounts were subjected to vertical cyclic displacements with increasing amplitude: 5, 10, and 20 mm. To consider the effect of the rate of loading, four loading frequencies were assumed for each displacement amplitude: 0.25, 0.5, 1, and 3 Hz (Fig. 13). In the bending–shear direction, the cyclic behavior of the mounts was assessed by applying horizontal displacements consisting of the same displacement time histories applied in the vertical direction (Fig. 13). Note that the input displacement amplitudes correspond, roughly, to shear strains of 2.7, 5.4, and 11.4%.
 |
Fig. 12 Actual (left) and FE model (right) of the OLS. |
 |
Fig. 13 Input displacement time histories (for both loading cases). |
4.2 Material data
4.2.1 Compound's material
The compound's material consists of rubber, which is known for its damping properties and has been used in many shock and vibration isolation mounts [24,25]. High damping rubbers exhibit both hyperelasticity and viscoelasticity, hence are modeled using hyper-viscoelastic constitutive material models.
Different constitutive models are available to represent the hyperelasticity of rubber-like materials [26]. In this study, Ogden model [27] is used to simulate the rubber behavior, which is defined using the strain energy potential function in the form: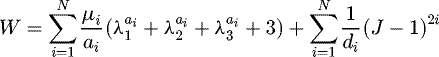 (24)in which, the initial shear modulus, μi, is given by:
(24)in which, the initial shear modulus, μi, is given by: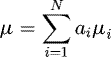 (25)and the initial bulk modulus is:
(25)and the initial bulk modulus is: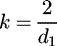 (26)
(26)
In equation (24), μi and ai are the primary fitting parameters, λi(i = 1, 2, 3) represents three principal stretches, and N is the material constant (N ≤ 3) and represent the fitting parameters to the volumetric deformation and material Jacobian, respectively. The formulas for stress given strain can be derived from the strain energy potential function (Eq. (24)). By using experimental test data, a least-squares fit of the stress–strain equations can be computed to determine the parameters of the hyperelastic model [28–31].
The viscoelasticity, on the other hand, combines both, elasticity and viscosity. The elastic behavior characterizes the tendency of the material to store energy while the viscosity characterizes its tendency to dissipate that energy. The combination of such behaviors leads to a rate-dependent behavior. Therefore, modeling of viscoelastic materials requires nonlinear constitutive laws to describe their complex behavior. In most FEA software, the viscoelasticity is modeled using Prony series, in which the shear modulus is expressed as follows: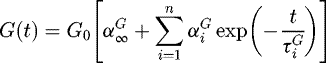 (27)where G0 is the relaxation shear modulus at time t = 0; n is the number of Prony terms;
(27)where G0 is the relaxation shear modulus at time t = 0; n is the number of Prony terms; 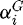 is the relative modulus,
is the relative modulus, 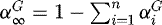 ; and
; and 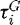 is the relaxation time.
is the relaxation time.
In the current investigation, the damping compound's material data are selected as shown in Figure 14. The parameters of the compound's material (at room temperature) were taken from Zhang et al. [32] and consist of the following:
Ogden three-data points model of the hyperelastic behavior (Fig. 14(a)): mu1 = 18.9 × 105 Pa, mu2 = 3.6 × 103 Pa, mu3 =−3 × 104 Pa, a1 = 1.3, a2 = 5, a3 =−2;
Prony series model of the viscoelastic behavior (Fig. 14(b)): α1 = α2 = 1/3, τ1 = 0.4 s, τ2 = 0.2 s.
 |
Fig. 14 Material data for rubber: (a) hyperelasticity and (b) viscoelasticity. |
4.2.2 Face plates material
The steel material of the face plates is represented by a bilinear model with kinematic strain hardening (Fig. 15) with young's modulus Ef = 193 GPa, yield stress σy = 240 MPa, strain hardening modulus Et = 0.01 Ef, and Poisson's ratio νf = 0.3.
 |
Fig. 15 Material data for steel. |
4.3 Results and discussion
First, a small static displacement was applied to the four OLS mounts to determine their static stiffness in both, vertical and lateral directions. The obtained stiffness values are reported in Table 7 along with those computed using equations (22) and (23). A good agreement between the two approaches is achieved. As the compound thickness increases, the theoretical solution becomes more accurate. Mounts with very thin compounds, such as OLS1 are not very practical for their low damping properties. Therefore, the proposed equations are more accurate for the range of practical geometries.
In what follows the cyclic behavior of vibration mounts is discussed with respect to the two loading cases under different cyclic motion frequencies.
Comparison of static stiffness determined using FEA and theory.
4.3.1 Vertical cyclic behavior
For the vertical (compression/tension) direction, the force–displacement curves of the four OLS mounts are shown in Figure 16. For clarity, only two cyclic motion frequencies are reported: 0.25 Hz and 3 Hz. All mounts exhibited asymmetric hysteresis behavior. The mounts showed softening behavior while in compression and hardening behavior in tension. The difference between the tensile and compressive stiffnesses is related to the tensile/compressive stiffness of the rubber, as well as the compressive stiffness being influenced by additional factors such as geometry characteristics. Similar observations were reported by [33]. In addition, in the vertical direction, the mounts are softer when subjected to low frequency motions and stiffer under higher frequencies.
Under high loading frequency (i.e., 3 Hz), the hysteresis loops are narrower, indicating low energy dissipation and almost linear behavior, especially for mounts with thin rubber compound (e.g., OLS1). As the loading frequency decreases, the hysteresis loops become wider, suggesting higher energy dissipation capability, particularly for the mounts with thicker compound.
To check the contribution of the steel material nonlinearity on the overall behavior of the OLS mounts, a linear steel material (with Ef = 193 GPa and νf = 0.3) was assumed for the face-plates while keeping the compound's material as is (i.e., hyper-viscoelastic) in a new series of FEA. Figure 17(a) clearly demonstrates that the hysteresis behavior of OLS4, for example, is not affected by the nonlinearity of the steel, suggesting that both, the stiffness and energy dissipation per cycle are not dependent on the face-plates material nonlinearity, at least up to the highest considered level of loading amplitude (i.e., 20 mm).
 |
Fig. 16 Vertical force–displacement curves for two loading frequencies. |
 |
Fig. 17 Effect of the face-plates material nonlinearity on the hysteresis behavior of OLS4 mount at 0.25 Hz loading frequency. |
4.3.2 Lateral cyclic behavior
Figure 18 shows the force–displacement curves of OLS mounts in the in-plane (bending–shear) horizontal direction. The response of the OLS mounts showed linear behavior when subjected to small displacement amplitudes (i.e., 5 mm), and nonlinear behavior for larger amplitudes. Under high frequency lateral loadings (i.e., 3 Hz), the hysteresis loops are narrower, however, they become wider for thicker compound mounts. In the lateral direction, the mounts are softer when subjected to low frequency motions and stiffer under higher frequencies.
The stiff response at small displacement amplitudes is desirable to limit the horizontal movement of isolated equipment during high frequency vibrations. At large loading amplitudes, the flexibility of the isolators lengthens the period of the isolated equipment, thus reducing the acceleration response. Unlike in the vertical direction, the hysteresis loops were larger and symmetric in the lateral direction (see Fig. 18). The amount of energy dissipated per cycle is highly dependent on both, the amplitude and the rate of loadings. As in the vertical direction, Figure 17(b) shows that in the lateral direction, the hysteresis behavior is not affected by the nonlinearity of the steel face-plates, at least up to the highest considered level of loading amplitude (i.e., 20 mm).
 |
Fig. 18 Lateral force–displacement curves for two loading frequencies. |
4.3.3 Effective stiffness and energy dissipation
To further characterize the cyclic response of the OLS mounts, the effective stiffness and energy dissipation per cycle were determined for each loading frequency and amplitude. The effective stiffness for each cycle is calculated for units with viscoelastic behavior as per Eurocode 8 [34]: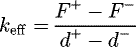 (28)in which d+ and d− are the maximum positive, respectively, the maximum negative displacement achieved by the OLS, while F+ and F− are the corresponding force reactions. The energy dissipated per cycle, which serves as an estimate of the level of damping, is calculated as the area under the hysteresis loop.
(28)in which d+ and d− are the maximum positive, respectively, the maximum negative displacement achieved by the OLS, while F+ and F− are the corresponding force reactions. The energy dissipated per cycle, which serves as an estimate of the level of damping, is calculated as the area under the hysteresis loop.
4.3.3.1 Effective stiffness
Figure 19 shows the effective stiffness determined at 20 mm displacement amplitude as a function of loading frequency. In both loading directions, the effective stiffness increases with the frequency, however, regardless of the loading rate, the effective stiffness in the vertical direction is always higher than in the lateral direction. The increase in the effective stiffness with the frequency is attributed, in part, to the property of rubber viscoelasticity, where the shear modulus increases with the frequency. The effective stiffness of all OLS mounts in both directions is more sensitive to the change in loading frequency in the range of 0.25–1 Hz than in the range 1–3 Hz.
Tables 8 and 9 report the percentage of change in the effective stiffness of the four OLS mounts from 0.25 Hz to 3 Hz loading frequencies in the vertical and lateral directions, respectively. Clearly, for mounts with thinner compounds, the effective stiffness increases by smaller amounts and as the compound becomes thicker, the increase can reach up till 30% in the vertical direction and 70% in the lateral direction. Note that in the lateral direction, the effective stiffness increases by larger amounts compared to the vertical direction.
Moreover, the effective stiffness is almost insensitive to the change in loading amplitude, until 20 mm (see Figs. 20 and 21).
 |
Fig. 19 Variation of the effective stiffness (at 20 mm displacement amplitude) with the frequency of loading in the (a) vertical and (b) lateral directions. |
Percentage of increase of the vertical effective stiffness from 0.25 Hz loading frequency to 3 Hz.
Percentage of increase of the lateral effective stiffness from 0.25 Hz loading frequency to 3 Hz.
 |
Fig. 20 Effect of the loading amplitude on the vertical effective stiffness. |
 |
Fig. 21 Effect of the loading amplitude on the lateral effective stiffness. |
4.3.3.2 Energy dissipation
The variation of the cumulative dissipated energy with the loading frequency is shown in Figure 22. From 0.25 Hz to 0.5 Hz, the cumulative dissipated energy increases, reaching the peak at 0.5 Hz suggesting that the material is more dissipative at this frequency, then decreases at higher frequencies, especially for mounts with thick damping compounds. Furthermore, when loaded in the lateral direction, the OLS mounts dissipate more energy than in vertical direction.
Unlike the trend seen in the effective stiffness, the energy dissipated per cycle increases with the loading amplitude (Figs. 23 and 24). Noticeably, the OLS mounts are more suitable to isolate equipment subjected to low frequency, high amplitude vibrations.
 |
Fig. 22 Cumulative dissipated energy in the (a) vertical and (b) lateral directions. |
 |
Fig. 23 Effect of the loading amplitude on the energy dissipated per cycle in the vertical direction. |
 |
Fig. 24 Effect of the loading amplitude on the energy dissipated per cycle in the lateral direction. |
5 Conclusions
In this study, analytical models have been developed to estimate the elastic stiffness of the Oval Leaf Spring mounts (OLS) under unidirectional line-loading configuration. The FEA performed on several OLS mounts proved the accuracy of the proposed theoretical expressions in predicting the spring stiffnesses in the vertical and horizontal in-plane directions, even with included transverse shearing effects. The developed analytical models satisfactory predict the behavior observed in the FEM results of the mounts, such as:
the major stiffness is in the vertical direction;
all spring stiffnesses increase with increase in thickness and width of the OLS but decrease with increase in radius;
the spring stiffnesses are more sensitive to the change in OLS radius than its thickness;
an increase in the damping compound thickness reduces the stiffness of the OLS mount in all directions;
the spring stiffness is highly dependent on the length of the flat surface; an increase in the length decreases the spring stiffness;
the compressive stiffness to the bending–shear stiffness ratio depends only on the face-plate length and spring radius.
Furthermore, to assess the effective stiffness and energy dissipation capacity of the mounts, a series of three-dimensional NLFEA have been carried out considering both, the hyper-viscoelastic behavior of the damping compound and the nonlinearity of the steel face-plates. The investigation has led to draw the following conclusions:
the force–displacement hysteretic loops of the OLS mounts show good energy dissipation capability under low frequency and this capacity increases with the loading amplitudes;
the effective stiffness increases with the frequency of loading;
the influence of the displacement amplitude on the effective stiffness is relatively smaller compared with the frequency of loading and thickness of the compound;
increasing the damping compound thickness enhances significantly the energy dissipation.
Acknowledgments
This paper is based upon the work supported by the University of Sharjah under the competitive grant scheme (Innovative Vibration Attenuation Devices for Equipment and Structures) and the National School of Built and Ground Works Engineering, Algeria.
References
- G.W. Housner, L. Bergman, T. Caughey, A. Chassiakos, R. Claus, S. Masri, R. Skelton, T. Soong, B. Spencer, J.T. Yao, Structural control: past, present, and future, J. Eng. Mech. 123 (1997) 897–971 [Google Scholar]
- S. Naranjo, L. Hong-Nan, L. Gang, Simple method for pushover curves of asymmetric structure with displacement-dependent passive energy dissipation devices, Summer Research Program in Marine Science and Engineering, Clarkson Univ. (USA) and Dalian Univ. of Technology (China), Dalian, China, 2006 [Google Scholar]
- RubberDesign: Rubber shock mountings, 2015, http://www.rubberdesign.nl/pdfs/downloads/shock-mountings/documentation-rubber-shock-mountings.aspx (online, accessed on: 2017/07/01) [Google Scholar]
- M.M. Shokrieh, D. Rezaei, Analysis and optimization of a composite leaf spring, Compos. Struct. 60 (2003) 317–325 [Google Scholar]
- E. Mahdi, O. Alkoles, A. Hamouda, B. Sahari, R. Yonus, G. Goudah, Light composite elliptic springs for vehicle suspension, Compos. Struct. 75 (2006) 24–28 [CrossRef] [Google Scholar]
- S. Kishiki, Y. Ohkawara, S. Yamada, A. Wada, Experimental evaluation of cyclic deformation capacity of U-shaped steel dampers for base-isolated structures, J. Struct. Construct. Eng., 73 (2008) 333–340 [CrossRef] [Google Scholar]
- S.I. Kwon, S.H. Oh, S.H. Lee, An analytical study on the shape development of ushaped steel damper for seismic isolation system, J. Korean Soc. Steel Construct. 22 (2010) 43–53 [Google Scholar]
- P. Tse, K. Lau, W. Wong, S. Reid, Spring stiffnesses of composite circular springs with extended flat contact surfaces under unidirectional line-loading and surface-loading configurations, Compos. Struct. 55 (2002) 367–386 [CrossRef] [Google Scholar]
- P. Tse, C. Lung, Large deflections of elastic composite circular springs under uniaxial tension, Int. J. Non-linear Mech. 35 (2000) 293–307 [CrossRef] [Google Scholar]
- S.H. Oh, S.H. Song, S.H. Lee, H.J. Kim, Experimental study of seismic performance of base-isolated frames with U-shaped hysteretic energy-dissipating devices, Eng. Struct. 56 (2013) 2014–2027 [CrossRef] [Google Scholar]
- S.H. Oh, S.H. Song, S.H. Lee, H.J. Kim, Seismic response of base isolating systems with U-shaped hysteretic dampers, Int. J. Steel Struct. 12 (2012) 285–298 [CrossRef] [Google Scholar]
- W. Wong, P. Tse, K. Lau, Y. Ng, Spring constant of fibre-reinforced plastics circular springs embedded with nickel-titanium alloy wire, Compos. Struct. 65 (2004) 319–328 [CrossRef] [Google Scholar]
- A. Treviso, B. Van Genechten, D. Mundo, M. Tournour, Damping in composite materials: properties and models, Compos. B: Eng. 78 (2015) 144–152 [Google Scholar]
- M. Ganapathi, B. Patel, P. Boisse, O. Polit, Flexural loss factors of sandwich and laminated composite beams using linear and nonlinear dynamic analysis, Compos. B: Eng. 30 (1999) 245–256 [CrossRef] [EDP Sciences] [Google Scholar]
- M. Hao, M.D. Rao, Vibration and damping analysis of a sandwich beam containing a viscoelastic constraining layer, J. Compos. Mater. 39 (2005) 1621–1643 [CrossRef] [Google Scholar]
- C.A. Verbaan, G.W. Peters, M. Steinbuch, The advantage of linear viscoelastic material behavior in passive damper design-with application in broad-banded resonance dampers for industrial high-precision motion stages, J. Sound Vib. 386 (2017) 242–250 [CrossRef] [Google Scholar]
- A. De Lima, B. Guaraldo-Neto, T. Sales, D. Rade, A time-domain modeling of systems containing viscoelastic materials and shape memory alloys as applied to the problem of vibration attenuation, Eng. Struct. 68 (2014) 85–95 [CrossRef] [EDP Sciences] [Google Scholar]
- Z.D. Xu, F.H. Xu, X. Chen, Vibration suppression on a platform by using vibration isolation and mitigation devices, Nonlinear Dyn. 83 (2016) 1341–1353 [CrossRef] [Google Scholar]
- N. Choudhary, D. Kaur, Vibration damping materials and their applications in nano/micro-electro-mechanical systems: a review, J. Nanosci. Nanotechnol. 15 (2015) 1907–1924 [CrossRef] [PubMed] [Google Scholar]
- W. Arshad, Static and buckling analyses of curved metallic and composite beams using hierarchical fem, Ph.D. thesis, Concordia University, 2005 [Google Scholar]
- A.P. Boresi, R.J. Schmidt, O.M. Sidebottom, Advanced mechanics of materials, vol. 5, Wiley, New York, 1993 [Google Scholar]
- S. Timoshenko, Strength of materials, in: Advanced theory and problems, Part II, D. Van Nostrand Company, Inc., New York, 1940 [Google Scholar]
- O. Elsherif, Lateral buckling of horizontally curved beams, Ph.D. thesis, Polytechnic Institute of New York University, 2009 [Google Scholar]
- C. Lewitzke, P. Lee, Application of elastomeric components for noise and vibration isolation in the automotive industry, Tech. Rep., SAE Technical Paper, 2001 [Google Scholar]
- J.H. Wu, C.H. Li, H.T. Chiu, Z.J. Shong, Dynamic properties of rubber vibration isolators and antivibration performance of ethylene–propylene–diene monomer/nylon 6 blend systems, J. Appl. Polym. Sci. 108 (2008) 4114–4121 [CrossRef] [Google Scholar]
- M.C. Boyce, E.M. Arruda, Constitutive models of rubber elasticity: a review, Rubber Chem. Technol. 73 (2000) 504–523 [CrossRef] [Google Scholar]
- R. Ogden, Large deformation isotropic elasticity-on the correlation of theory and experiment for incompressible rubberlike solids, Rubber Chem. Technol. 46 (1973) 398–416 [CrossRef] [Google Scholar]
- R. Ogden, G. Saccomandi, I. Sgura, Fitting hyperelastic models to experimental data, Comput. Mech. 34 (2004) 484–502 [Google Scholar]
- P. Martins, R. Natal Jorge, A. Ferreira, A comparative study of several material models for prediction of hyperelastic properties: application to silicone-rubber and soft tissues, Strain 42 (2006) 135–147 [CrossRef] [EDP Sciences] [Google Scholar]
- G. Marckmann, E. Verron, Comparison of hyperelastic models for rubber-like materials, Rubber Chem. Technol. 79 (2006) 835–858 [CrossRef] [Google Scholar]
- L. Yang, V. Shim, C. Lim, A visco-hyperelastic approach to modelling the constitutive behaviour of rubber, Int. J. Impact Eng. 24 (2000) 545–560 [CrossRef] [Google Scholar]
- X. Zhang, S. Yang, L. Chen, Finite element simulation of viscoelastic damping materials, in: Advanced Intelligent Computing Theories and Applications. With Aspects of Contemporary Intelligent Computing Techniques, Springer, 2007, pp. 1234–1241 [CrossRef] [Google Scholar]
- F. Tajirian, J. Kelly, I. Aiken, W. Veljovich, Elastomeric bearings for three-dimensional seismic isolation, in: 1990 ASME PVP Conference, Nashville, TN, USA, 1990 [Google Scholar]
- CEN, Eurocode 8: Design provisions of structures for earthquake resistance, Part 2: Bridges, en1998-2: 2005, European Committee for Standardization, Brussels, 2005 [Google Scholar]
Cite this article as: A. Benyoucef, M. Leblouba, A. Zerzour, Stiffness and energy dissipation of Oval Leaf Spring mounts under unidirectional line loading, Mechanics & Industry 18, 414 (2017)
All Tables
Comparison of numerical and theoretical stiffness of OLS mounts with Ec = 0.05Ef.
Percentage of increase of the vertical effective stiffness from 0.25 Hz loading frequency to 3 Hz.
Percentage of increase of the lateral effective stiffness from 0.25 Hz loading frequency to 3 Hz.
All Figures
 |
Fig. 1 The Oval Leaf Spring (OLS). |
| In the text | |
 |
Fig. 2 OLS geometric properties. |
| In the text | |
 |
Fig. 3 OLS subjected to vertical compressive load. |
| In the text | |
 |
Fig. 4 OLS subjected to bending–shear load. |
| In the text | |
 |
Fig. 5 Variation of the OLS stiffness with thickness and radius (Ec = Ef). |
| In the text | |
 |
Fig. 6 Variation of the OLS stiffness with thickness and width (Ec = Ef). |
| In the text | |
 |
Fig. 7 Variation of the average normalized stiffness with t and nE. |
| In the text | |
 |
Fig. 8 Variation of the average normalized stiffness with nt and nE. |
| In the text | |
 |
Fig. 9 Variation of the average normalized stiffness with R and L. |
| In the text | |
 |
Fig. 10 Variation of the average normalized stiffness with L and R. |
| In the text | |
 |
Fig. 11 Comparison of OLSs stiffness ratios. |
| In the text | |
 |
Fig. 12 Actual (left) and FE model (right) of the OLS. |
| In the text | |
 |
Fig. 13 Input displacement time histories (for both loading cases). |
| In the text | |
 |
Fig. 14 Material data for rubber: (a) hyperelasticity and (b) viscoelasticity. |
| In the text | |
 |
Fig. 15 Material data for steel. |
| In the text | |
 |
Fig. 16 Vertical force–displacement curves for two loading frequencies. |
| In the text | |
 |
Fig. 17 Effect of the face-plates material nonlinearity on the hysteresis behavior of OLS4 mount at 0.25 Hz loading frequency. |
| In the text | |
 |
Fig. 18 Lateral force–displacement curves for two loading frequencies. |
| In the text | |
 |
Fig. 19 Variation of the effective stiffness (at 20 mm displacement amplitude) with the frequency of loading in the (a) vertical and (b) lateral directions. |
| In the text | |
 |
Fig. 20 Effect of the loading amplitude on the vertical effective stiffness. |
| In the text | |
 |
Fig. 21 Effect of the loading amplitude on the lateral effective stiffness. |
| In the text | |
 |
Fig. 22 Cumulative dissipated energy in the (a) vertical and (b) lateral directions. |
| In the text | |
 |
Fig. 23 Effect of the loading amplitude on the energy dissipated per cycle in the vertical direction. |
| In the text | |
 |
Fig. 24 Effect of the loading amplitude on the energy dissipated per cycle in the lateral direction. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


