| Issue |
Mechanics & Industry
Volume 18, Number 5, 2017
|
|
|---|---|---|
| Article Number | 501 | |
| Number of page(s) | 17 | |
| DOI | https://doi.org/10.1051/meca/2016026 | |
| Published online | 25 August 2017 | |
Regular Article
Impact of aspect ratio on a nanofluid-saturated porous enclosure
Department of Mathematics, Bharathiar University, Coimbatore 641046, India
⁎ e-mail: muthtamil1@yahoo.co.in
Received: 16 November 2015
Accepted: 28 March 2016
The aim of the present numerical simulation is to investigate the mixed convection flow and heat transfer characteristics in a two dimensional porous cavity filled with nanofluid for different aspect ratios. The top and bottom walls are assumed to have the uniform temperatures θh and θc, respectively, with θh > θc while the vertical walls are kept to be adiabatic. The governing equations are solved by using finite volume method with the SIMPLE algorithm. The variations of isotherms, streamlines, mid-plane velocity profiles, and Nusselt numbers were discussed in detail over a wide range of pertinent parameters, viz., aspect ratio, Richardson number, Darcy number, and solid volume fraction. Although the addition of nanoparticles in the porous medium is to increase the overall heat transfer rate in most flow regimes, the overall heat transfer rate is appeared to decrease slightly or stay nearly the same with the increase of solid volume fraction for Ar = 0.25 and 0.5 porous cavities in the forced convection regime.
Key words: aspect ratio / mixed convection / porous cavity / nanofluid
© AFM, EDP Sciences 2017
1 Introduction
The problem of convective heat transfer in porous media has been major topic for research studies due to its fundamental nature and the wide spectrum of engineering applications such as geothermal energy systems, oil recovery, subsoil water filtration, nuclear waste storage, and chemical separation processes. Numerous studies have been done on convective heat transfer inside the porous enclosures. Khanafer and Chamkha [1] studied laminar mixed convection flow in an enclosure filled with a fluid-saturated porous medium. Their results demonstrated the significant suppression of the convective currents in the presence of a porous medium. Jue [2] performed a numerical study on thermal convection flow in a fluid-saturated porous cavity with internal heat generation. He has summarized that a proper adjustment of the porous media is to control the heat transfer rate as well as the direction of heat transfer. Partially cooled and inclined porous rectangular enclosures were studied by Oztop [3]. It is concluded that inclination angle and aspect ratio are the dominant parameters on heat transfer and fluid flow in the porous enclosures. Misirlioglu [4] conducted a numerical study to investigate the mixed convection flow in a square cavity filled with porous medium. It is found that rotation of circular cylinder inside the cavity is more effective in the forced convection regime, and the heat transfer is almost independent from the Darcy number at high spin velocities. Vishnuvardhanarao and Das [5] numerically investigated the mixed convection flow in a parallel two-sided lid-driven differentially heated square porous enclosure. The average Nusselt number attains the value of 1 asymptotically when the Richardson number is gradually increased for Gr up to 103. Chamkha and Al-Mudhaf [6] have performed numerical investigation of double-diffusive natural convection in inclined porous cavities with various aspect ratios and temperature dependent heat source or sink. It is found that the fluid flow and heat transfer inside the porous enclosure depend strongly on the buoyancy ratio, cavity inclination angle and the heat generation or absorption effects. Basak et al. [7] studied on mixed convection flows in a cavity filled with porous medium with linearly heated side walls. Their results have shown that the average Nusselt numbers of bottom, left and right walls of the cavity are found almost invariant with Gr for low Pr with all Da for linearly heated side walls or cooled right wall.
Since the fluids such as water, mineral oils, and ethylene glycol have a rather low thermal conductivity and do not meet the growing demand in the heat transfer exchange, it is required to develop the new types of fluids, which should be more effective in heat transfer performance. Nanofluids, base pure fluids with suspended metallic nanoparticles, are such a new kind of fluids to fulfill the rising demand in the heat transfer exchange. Khanafer and Vafai [8] presented a numerical study on heat transfer enhancement in a 2-D enclosure utilizing nanofluids. It is observed that the structure of the fluid flow is altered in the presence of nanoparticles. Convective heat transfer in 2-D rectangular cavity utilizing nanofluids was investigated by Jou and Tzeng [9]. They have shown that the overall heat transfer rate is increased with the increase in the buoyancy parameter and volume fraction of nanofluids. Hwang et al. [10] theoretically studied the thermal characteristics of natural convection in a rectangular cavity filled with a water-based nanofluid containing alumina. Ho et al. [11] observed that the heat transfer in a square cavity filled with nanofluids could be enhanced or diminished depending on the formulas used to estimate the dynamic viscosity of the nanofluid. Numerical simulations on heat transfer due to mixed convection with nanofluid have been investigated by Mansour et al. [12]. The investigation concluded that even though an increase in solid volume fraction is to decrease both of activity of the fluid motion and fluid temperature, the overall heat transfer is augmented on increasing the solid volume fraction. Muthtamilselvan et al. [13] conducted a numerical analysis on the heat transfer enhancement of copper-water nanofluids in a lid-driven cavity. It is observed that both the aspect ratio and solid volume fraction affect the fluid flow and heat transfer rate in the enclosure. Ghasemi and Aminossadati [14] have reported a numerical study on convective heat transfer in triangular cavity filled with nanofluids. Their results have shown that a stronger flow circulation within the enclosure is observed when the motion of sliding wall is downward and hence, the higher heat transfer rate is obtained.
Even though several numerical studies of convection in heated enclosure containing nanofluids or porous medium are published, most of them concentrate separately on nanofluids and porous medium in cavities, and only few of them consider the porous medium filled with nanofluids. Nield and Kuznetsov [15] studied the Cheng and Minkowycz's problem [16] for natural convective boundary layer flow of nanofluid in a porous medium. In their study, for the nanofluid the effects of Brownian motion and thermophoresis are incorporated and for the porous medium the Darcy model is used. Kuznetsov and Nield [17] developed a theory of double-diffusive nanofluid convection in porous media. They predicted that for the case when Soret and Dufour parameters are negligible, the non-oscillatory mode is expected when Rn is positive, a situation which physically corresponds to the fact that for oscillations to occur two of the buoyancy forces have to be in opposite directions. Ahmad and Pop [18] reported on the steady of mixed convection boundary layer flow past a vertical flat plate embedded in a porous medium filled with nanofluids. Mittal et al. [19] performed a numerical study on mixed convection flow in porous medium filled nanofluid. Their numerical simulations have shown that a higher heat transfer rate is obtained by adding the nanoparticles to base fluid in the porous medium. Nguyen et al. [20] made a numerical analysis on laminar natural convective flow in non-Darcy porous enclosure filled with nanofluid. Their results have revealed that increasing the solid volume fraction decreases the overall heat transfer rate in Darcy flow regime at a high Rayleigh number and low Darcy number. Zhang et al. [21] presented a numerical study on MHD flow and radiation heat transfer of nanofluids in porous media with the effects of variable surface heat flux and chemical reaction. It is found that velocity and temperature fields are strongly affected in the presence of magnetic field and radiation effects.
Only few of published works focused on momentum and energy transfer in porous cavity filled with nanofluids. Complementary works are needed to understand the fluid flow and heat transfer characteristics of nanofluids in porous cavity. It is also found from the review of the above literature that mixed convection flow in porous cavity filled with nanofluid with various aspect ratios is not reported so far. To fulfill the above need, the present study aims to examine the laminar mixed convection flow of a nanofluid in porous cavity with different types of aspect ratios. Specifically, the aim of present work is to examine numerically the effects of Darcy number, Richardson number, aspect ratio, and solid volume fraction of nanoparticles.
2 Mathematical analysis
Figure 1(a) presents a schematic diagram of physical configuration of the present study. The system is considered to be steady, laminar, incompressible mixed convective flow and heat transfer in 2-D square porous cavity of height H and length L filled with nanofluid. The top and bottom walls are assumed to have the uniform temperatures θh and θc, respectively, with θh > θc. The side walls are considered to be thermally insulated. The velocity components u and 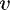 are taken in x and y directions respectively. No slip condition is assumed between the fluid and two vertical walls. Further, the tangential fluid velocity is considered to equal the moving wall velocity. The top wall of the cavity is moving from left to right with constant speed U0. The porous cavity is filled with nanofluid, which is made of a base fluid (water) and spherical nanoparticles (Cu). The fluid in the cavity is Newtonian and incompressible. The porous medium is taken as hydrodynamically and thermally isotropic and saturated with a fluid that is local thermal equilibrium (LTE) model with the solid matrix. It is assumed that the base fluid (water) and spherical nanoparticles (Cu) are in thermally equilibrium and no-slip velocity between them. The fluid physical properties are assumed to be constant except the density variation in the buoyancy term. The Boussinesq approximation is valid. The thermophysical properties of the base fluid and nanoparticles are shown in Table 1. The governing equations consisting of mass, momentum and energy equations for the mixed convection of the nanofluid in the 2-D porous cavity can be written in the dimensional form as follows:
are taken in x and y directions respectively. No slip condition is assumed between the fluid and two vertical walls. Further, the tangential fluid velocity is considered to equal the moving wall velocity. The top wall of the cavity is moving from left to right with constant speed U0. The porous cavity is filled with nanofluid, which is made of a base fluid (water) and spherical nanoparticles (Cu). The fluid in the cavity is Newtonian and incompressible. The porous medium is taken as hydrodynamically and thermally isotropic and saturated with a fluid that is local thermal equilibrium (LTE) model with the solid matrix. It is assumed that the base fluid (water) and spherical nanoparticles (Cu) are in thermally equilibrium and no-slip velocity between them. The fluid physical properties are assumed to be constant except the density variation in the buoyancy term. The Boussinesq approximation is valid. The thermophysical properties of the base fluid and nanoparticles are shown in Table 1. The governing equations consisting of mass, momentum and energy equations for the mixed convection of the nanofluid in the 2-D porous cavity can be written in the dimensional form as follows: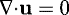 (1)
(1) (2)
(2)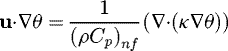 (3)where u is the Darcy velocity vector, p is the fluid pressure, θ is the temperature, and ε is the porosity of the medium. The permeability K and Forchheimer's coefficient F can be written as
(3)where u is the Darcy velocity vector, p is the fluid pressure, θ is the temperature, and ε is the porosity of the medium. The permeability K and Forchheimer's coefficient F can be written as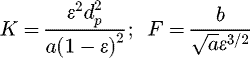 where a = 150 and b = 1.75. The appropriate dimensional forms of the boundary conditions are given as follows:
where a = 150 and b = 1.75. The appropriate dimensional forms of the boundary conditions are given as follows: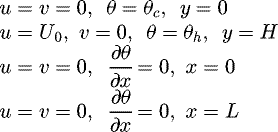 (4)
(4)
The above dimensional form of mass, momentum and energy equations can be converted to non-dimensional form by using the following dimensionless parameters: (5)
(5)
After non-dimensionalization, the above dimensional form of governing equations can now be written as follows: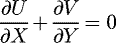 (6)
(6)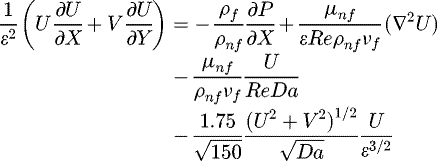 (7)
(7)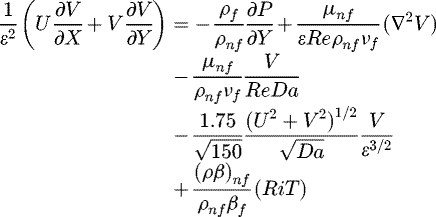 (8)
(8)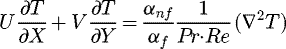 (9)
(9)
The non-dimensional boundary conditions of the considered problem are given as follows: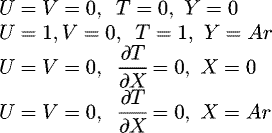 (10)
(10)
The properties of the nanofluids are given in Table 2.
The local and average heat transfer rates of the cavity can be presented by means of the local and average Nusselt numbers. The local Nusselt number for the consider problem is calculated along the top heated wall and the average Nusselt number (Nuavg) for overall heat transfer rate is obtained by integrating the local Nusselt number.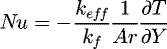 (11)
(11)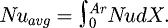 (12)
(12)
Many researchers have cited the classical Maxwell [22] model in which only the particle volume concentration and the thermal conductivities of the particle are considered but the Brownian motion of the nanoparticles and the effect of solid like nano-layers formed around nanoparticles are not taken into the account. To execute the above need the modified Maxwell [23] model considers a nano-layer with a solid like structure formed by the liquid molecules close to solid surface. As far as the modified Maxwell model is concerned, keff is the effective thermal conductivity of the nanofluid for spherical nanoparticles, which is given as follows: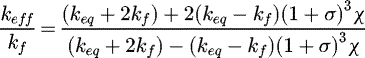 (13)where σ is the ratio of the thickness of nano-layer to the original radius of nanoparticles (hnl/rs) and keq is the equivalent thermal conductivity of nanoparticles and their layers:
(13)where σ is the ratio of the thickness of nano-layer to the original radius of nanoparticles (hnl/rs) and keq is the equivalent thermal conductivity of nanoparticles and their layers: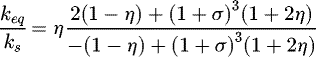 (14)where η is the ratio of thermal conductivity of nano-layer upon the thermal conductivity of the nanoparticles (η = knl/ks). In this study, it is assumed that hnl = 2nm, rs = 3nm and knl = 100kf. Yu and Choi [23] obtained that for these conditions, the result of the modified Maxwell model are in good agreement with experimental results.
(14)where η is the ratio of thermal conductivity of nano-layer upon the thermal conductivity of the nanoparticles (η = knl/ks). In this study, it is assumed that hnl = 2nm, rs = 3nm and knl = 100kf. Yu and Choi [23] obtained that for these conditions, the result of the modified Maxwell model are in good agreement with experimental results.
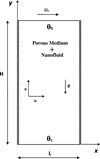 |
Fig. 1 A schematic view of the considered cavity in the present study. |
Thermophysical properties of water and nanoparticles.
Applied formulae for the nanofluid properties.
3 Numerical technique and validation
3.1 Numerical method
The governing equations (6)–(9) subject to the boundary conditions are discretized by the finite volume method (FVM) on a uniform staggered grid arrangement using SIMPLE algorithm of Patankar [24]. The third order accurate deferred QUICK scheme of Hayase et al. [25] and central difference scheme are applied for the convection and diffusion terms in the both momentum and energy equations. The uniform grid is selected in both X and Y directions. The solution domain consists of a number of control volumes at which discretization equations are applied. The governing equations are transferred into a system of algebraic equations through integration over each control volume. The solution of the discretized equations for each variable is obtained by TDMA line-by-line method. The grid independence tests are carried out using the grid points from 11 × 21 to 81 × 161 for Ri = 100, Pr = 6.2, ε = 0.4, Da = 10−2, Ar = 0.5 and χ = 0.06. The grid independence test which is shown in Figure 2(a) demonstrated that an 41 × 81 grid system is enough to obtain the desired accuracy of results.
 |
Fig. 2 (a) Mid-plane U-velocity for different mesh sizes at Ri = 100, Da = 10−2, ε = 0.4, χ = 0.06, and Ar = 0.5, (b) comparisons of the local Nusselt numbers with the results of Roy and Basak [26] and (c) the mid-plane velocity profiles of Mahmoodi et al. [27]. |
3.2 Code validation
In order to check the accuracy of the present results, the present computational code has been validated by two published work in the literature. The direct validation of the present numerical model against the numerical results of Roy and Basak [26] was performed. Comparisons of the local Nusselt number along the bottom wall for uniform heating are shown in Figure 2(b). In this case, the agreement is found to be excellent. The results for combined convection in lid driven enclosure filled with nanofluid were also compared with Mahmoodi et al. [27]. A comparison of the dimensionless vertical velocity component along the horizontal centerline of the cavity for Ri = 100 and χ = 0.03 are executed in Figure 2(c) and show a good agreement. The results compared with the previous literature provide confidence to the accuracies of the present numerical solutions.
4 Results and discussion
In this paper, a numerical study has been presented to investigate the mixed convection flow and heat transfer characteristics in a two dimensional porous cavity filled with Cu-water nanofluid. The present computations were carried out to determine the effects of the aspect ratio (0.25 ≤ Ar ≤ 2), the Richardson number (0.01 ≤ Ri ≤ 100), the Darcy number (10−4 ≤ Da ≤ 10−2), and the solid volume fraction (0 ≤ χ ≤ 0.06). Throughout the study, the porosity ε = 0.4 is fixed. The copper-water nanofluid is chosen as working fluid with the Prandtl number Pr = 6.2. The computational results are shown in terms of isotherms, streamlines, mid-plane velocity profiles, and local as well as average Nusselt numbers for various physical parameters.
The effects of Richardson number and aspect ratio on the fluid flow and thermal field for Da = 10−2 and χ = 0.06 are depicted in Figures 3–6. For the aspect ratio Ar = 0.25 (Fig. 3), the flow field is described by a primary vortex near top moving lid and two weaker secondary eddies, which occurs one below the other in the remaining part of the cavity when Ri = 100. As Ri decreases (Ri < 1), the primary vortex near top moving lid starts to grow bigger and two weaker secondary eddies are merged. Since this is slender cavity, the effect of the shear force can be observed only in one unit of the cavity height where the flow recirculation is prominent. In the remaining part of the cavity, the flow of nanofluid remains almost stagnant. The isotherms specify that a high temperature gradients are observed only at the location near top wall and conduction is the principal mode of heat transfer in the rest space of the cavity for all Ri varied. Figure 4 shows that the hot and cold walls of the porous enclosure come closer and convection gets stronger as the aspect ratio increases from 0.25 to 0.5. A tri-cellular flow structure is appeared with two clockwise rotating eddies at the top and bottom of the cavity and one anti-clockwise rotating vortex at the middle when Ri = 100. It is observed that the flow structure is always of two symmetric eddies only at the top and bottom of the cavity for Ri ≤ 1. A decrease in Ri clusters the temperature gradients downwards markedly. The isotherms and streamlines for Ar = 1 and 2 are depicted in Figures 5 and 6. In the both aspect ratios Ar = 1 and 2, a symmetric behaviour is observed in the fluid flow and temperature field. It can be understood from these figures that for Ri = 100, two symmetrical counter rotating eddies are appeared at the top and bottom of the enclosure. The corresponding isotherms show high temperature gradients near top wall. When Ri decreases, that is, when the buoyancy effect is overwhelmed by the mechanical effect of the sliding lid, the two symmetrical counter rotating eddies are merged, a main circulation fills the entire cavity, and two secondary cells are visible near bottom corners (see Figs. 5(c) and 6(c)). The isotherms depict that the temperature distributions are grouped near bottom surface of the cavity and it is very weak in the interior region of the cavity due to the vigorous effect of the top-moving lid.
Figure 7 shows the variations of horizontal and vertical velocity components of the porous cavity for different Ri and Ar when the other parameters are kept fixed. The velocity profiles reveal that the effects of aspect ratio play a major role on the flow field. It is observed that for Ar = 0.25, U-velocity decreases with the decrease of Ri. On the other hand, V-velocity increases with a decrease in Ri. A similar behaviour of U and V velocity is observed for all aspect ratios when Ri decreases. Since the fluid flow in bulk of the cavity remains stagnant for Ar = 0.25, U-velocity is almost zero in three-fourths of the porous cavity and attains its maximum in the rest space where the fluid flow is prominent. The mechanical effect of moving lid is not considerable enough when the cavity is slender. It can be verified clearly in Figure 7(a) and (b). As the aspect ratio increases from 0.25 to 0.5 (Fig. 7(c) and (d)), the magnitude of U and V-velocity augments and the sign of V-velocity is reversed for all Ri compared with the previous case Ar = 0.25. This enhancement of U and V-velocity is due to the fact that the hot and cold walls of the porous enclosure come closer. Moreover, it is found that the mid-plane velocity increases significantly with the increase of the aspect ratio for all Ri considered. It is shown in Figure 7(e)–(h).
Figure 8 illustrates the influence of the aspect ratio and Richardson number on the local Nusselt number for the fixed values of Da = 10−2 and χ = 0.06. For all Ri, the distribution of local Nusselt number begins with high value at the left end, decreases towards the right end, and attains the minimum near the right end of the X-axis when Ar is fixed, as shown in Figure 8. It can be noticed that for the fixed value of Ar, an enhancement in the local Nusselt number is observed when Ri varies from 100 to 0.01. Moreover, an increase in the aspect ratio increases the local heat transfer rate for all Richardson number varied. It is interesting to note that for Ar = 0.5, the maximum of the local Nusselt number is obtained near the left end of the X- axis when Ri = 1 (see Fig. 8(b)). Figure 8 also reveals the fact that for Ri = 1 and 100, after the first half of the X-axis, the local Nusselt number converges almost equally and attains the same values when the aspect ratio is kept fixed. This is because the buoyancy force is substantial enough in comparison with shear force in the mixed and natural convection.
The effects of aspect ratio and solid volume fraction on the fluid flow and thermal field for Da = 10−2 and Ri = 1 can be viewed in Figures 9–12. The streamlines in Figure 9(a) confirm that for χ = 0, a tri-cellular flow structure with a anti-clockwise eddy in the middle and two clockwise eddies near top and bottom of the cavity is appeared. As the solid volume fraction increases, the anticlockwise eddy in the middle of the cavity develops from its actual size and squeezes the two clockwise eddies near top and bottom of the cavity. The isotherms show that the temperature distributions are nearly parallel to the horizontal walls of the cavity, which indicates the conduction heat transfer mode throughout the cavity except the region at top of the enclosure where a mechanically induced force occurs. In addition, no significant change in temperature distribution is observed as χ increases. Figure 10 shows that when the aspect ratio is increased from 0.25 to 0.5 and χ = 0, the flow structure is characterized by a primary cell in half size of the cavity and two secondary cells one bellow the other in the remaining part of the cavity. As χ increases, the recirculation of the primary vortex gets strengthened, two weaker cells are merged, and a anticlockwise cell appears in the bottom of the cavity. The corresponding isotherms demonstrate almost the same behaviour in order to compare with Ar = 0.25. However, convection gets reinforced when the aspect ratio is increased from 0.25 and 0.5. It can be seen from Figure 10. Figure 11 shows that when χ = 0, the flow structure indicate a single recirculating vortex inside the cavity. Moreover, a secondary vortex emerges near left-bottom corner. Since the nanoparticles has the tendency to reinforce the movement of the fluid inside the porous cavity, the main recirculation cell gets strengthened and the secondary vortex is deteriorated as the solid volume fraction increases. It is observed from Figure 11 that the temperature distributions are clustered towards the bottom of the cavity and show a steep temperature gradients along the left insulated wall. The thermal boundary layers elevate upwards as χ increases from 0 to 0.06, which indicates that addition of nanoparticles in porous enclosure is to reinforce the fluid flow and gives better heat transfer enhancement in the enclosure. A similar behaviour in streamlines and isotherms is observed for Ar = 2. It can be verified from Figure 12.
The effects of aspect ratio and solid volume fraction on velocity profiles for Ri = 1, Da = 10−2 are depicted in Figure 13. The porous medium within the cavity has tendency to resist the flow motion of nanofluid. As a result, the flow velocity in the mid-plane of the cavity is almost zero on increasing the solid volume fraction for the slender porous cavity (Ar = 0.25). This can clearly be understood from the horizontal velocity profiles at the mid-section of the cavity for Ar = 0.25 (see Fig. 13(a)). The addition of nanoparticles increases V-velocity markedly whereas it has no significant effect on U-velocity when Ar = 0.25 and 0.5. For Ar = 1 and 2, no significant effect on velocity profiles is observed as the solid volume fraction increases. Furthermore, it is found that the flow velocity increases significantly with the increase of aspect ratio and solid volume fraction in the porous cavity.
The variations of the local Nusselt numbers along the hot moving lid are shown in Figure 14 for different aspect ratio and solid volume fraction. The effects of aspect ratio and solid volume fraction on the heat transfer rate are clearly shown in these plots. In general, the local Nusselt numbers along the hot wall start with high value at the left end and decrease monotonically to a small value near the right end for all the considered values of χ when Ar is fixed. In addition, it can be understood that an increase in solid volume fraction increases the local Nusselt number for all aspect ratios. This reveals the fact that the heat transfer rate inside the porous cavity is directly affected on increasing the solid volume fraction. The maximum of local Nusselt number is obtained for Ar = 2, which indicates that the local heat transfer rate increases with the increase of aspect ratio in the porous enclosure. The overall heat transfer rate in terms of solid volume fraction for various aspect ratios and Richardson numbers is plotted in Figure 15. The overall heat transfer rate increases on increasing the aspect ratio. The curve of the average Nusselt number shows a linear variation with the solid volume fraction. An increase in average Nusselt number is obtained with the decrease of Richardson number for the fixed value of aspect ratio. Generally, the overall heat transfer rate increases with the increase of solid volume fraction. But, it is interesting to note that for Ri = 0.01, the average Nusselt number decreases slightly or stay nearly the same on increasing the solid volume fraction when Ar = 0.25 and 0.5. This can be verified in Figure 15(c). This is due to the fact that when Ar = 0.25 and 0.5, the strength of the anti-clockwise rotating cell is increased with the increase of solid volume fraction in the forced convection regime. In this way, the anti-clockwise rotating cell does not permit the fluid near the cold lid to move easily to the hot surface. Consequently, the overall heat transfer rate appears to decrease slightly or stay nearly the same with an increase in solid volume fraction for Ar = 0.25 and 0.5 when Ri = 0.01. Further, this indicates that adding the nanoparticles in base fluid may limit further enhancement of the heat transfer rate.
Figure 16 shows the overall heat transfer rate for different values of Richardson numbers, aspect ratios, and Darcy numbers with the fixed value of χ = 0.06. Since the low permeability (Da = 10−4) retards the fluid motion, the minimum heat transfer rate is obtained for Da = 10−4 whereas the maximum heat transfer rate occurs for Da = 10−2. For the fixed value of Ri, the average Nusselt number increases with the increase of aspect ratio. Generally, the high permeability (Da = 10−2) gives better heat transfer rate than the low permeability (Da = 10−4). But, in the slender porous cavity, i.e., in Ar = 0.25 and 0.5, high heat transfer rate is obtained for Da = 10−4 compared with Da = 10−2 when Ri = 0.01. This is shown in Figure 16. An increase in the overall heat transfer rate is observed by decreasing the Richardson number for the fixed values of aspect ratio and Darcy number.
 |
Fig. 3 Isotherms (left) and streamlines (right) for different Ri with ε = 0.4, Da = 10−2, Ar = 0.25, and χ = 0.06. |
 |
Fig. 4 Isotherms (left) and streamlines (right) for different Ri with ε = 0.4, Da = 10−2, Ar = 0.5, and χ = 0.06. |
 |
Fig. 5 Isotherms (left) and streamlines (right) for different Ri with ε = 0.4, Da = 10−2, Ar = 1, and χ = 0.06. |
 |
Fig. 6 Isotherms (left) and streamlines (right) for different Ri with ε = 0.4, Da = 10−2, Ar = 2, and χ = 0.06. |
 |
Fig. 7 U and V-velocity profiles at mid-plane of the cavity for different Ar and Ri with Da = 10−2, ε = 0.4, and χ = 0.06. |
 |
Fig. 8 Local Nusselt numbers for different Ar and Ri with Da = 10−2, ε = 0.4, and χ = 0.06. |
 |
Fig. 9 Isotherms (left) and streamlines (right) for different χ with ε = 0.4, Da = 10−2, Ri = 1, and Ar = 0.25. |
 |
Fig. 10 Isotherms (left) and streamlines (right) for different χ with ε = 0.4, Da = 10−2, Ri = 1, and Ar = 0.5. |
 |
Fig. 11 Isotherms (left) and streamlines (right) for different χ with ε = 0.4, Da = 10−2, Ri = 1, and Ar = 1. |
 |
Fig. 12 Isotherms (left) and streamlines (right) for different χ with ε = 0.4, Da = 10−2, Ri = 1, and Ar = 2. |
 |
Fig. 13 U and V-velocity profiles at mid-plane of the cavity for different Ar and χ with Da = 10−2, ε = 0.4, and Ri = 1. |
 |
Fig. 14 Local Nusselt numbers for different Ar and χ with Da = 10−2, ε = 0.4, and Ri = 1. |
 |
Fig. 15 Average Nusselt number. |
 |
Fig. 16 Average Nusselt number. |
5 Conclusion
In the present article, mixed convection flow of nanofluid in a square lid-driven cavity fully saturated with porous medium was numerically investigated for different aspect ratios. For Ar = 0.25 and 0.5, the fluid remains almost stagnant in the bulk of the cavity, which indicates the conduction dominated flow regime. Further, the convection gets strengthened with the increase of Ar. Consequently, the mid plane velocity increases with an increase in Ar. In the presence of nanoparticles, the magnitude of velocity and heat transfer rate increase remarkably with higher Ar and Da. Many researchers have found that the addition of nanoparticles in the porous medium is to increase the overall heat transfer rate in most flow regimes. To the contrary, the overall heat transfer rate is appeared to decrease slightly or stay nearly the same with increased solid volume fraction for Ar = 0.25 and 0.5 porous cavities in the forced convection regime. Since the resistance from the boundary friction is less at Da = 10−2, the fluid circulation is prominent within the enclosure for Da = 10−2 compared with Da = 10−4. As a result, a better heat transfer rate is obtained for Da = 10−2 than for Da = 10−4. In other words, the porous medium of high permeability gives better heat transfer rate than the porous medium of low permeability. It is also found that the better heat transfer rate is obtained with the porous cavity of high aspect ratio in order to compare with the slender porous cavity. By adding the nanoparticles to the base fluid in the porous medium, the overall heat transfer rate increases significantly.
Nomenclature
U, V: dimensionless velocities in x- and y-direction respectively
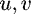 : velocities in x- and y-direction respectively
: velocities in x- and y-direction respectively
X, Y: dimensionless Cartesian coordinates
β: thermal expansion coefficient
η: ratio of thermal conductivity of nano-layers
σ: ratio of the thickness of nano-layer
Subscripts
Acknowledgment
This work was supported by SERB-DST, India. The authors thank SERB-DST, India for its financial support through this research project (SR/FTP/MS-025/2009).
References
- K.M. Khanafer, A.J. Chamkha, Mixed convection flow in a lid-driven enclosure filled with a fluid-saturated porous medium, Int. J. Heat Mass Transf. 42 (1999) 2465–2481 [CrossRef] [Google Scholar]
- T.C. Jue, Analysis of thermal convection in a fluid-saturated porous cavity with internal heat generation, Heat Mass Transf. 40 (2003) 83–89 [CrossRef] [Google Scholar]
- H.F. Oztop, Natural convection in partially cooled and inclined porous rectangular enclosures, Int. J. Therm. Sci. 46 (2007) 149–156 [Google Scholar]
- A. Misirlioglu, The effect of rotating cylinder on the heat transfer in a square cavity filled with porous medium, Int. J. Eng. Sci. 44 (2006) 1173–1187 [CrossRef] [Google Scholar]
- E. Vishnuvardhanarao, M.K. Das, Laminar mixed convection in a parallel two-sided lid-driven differentially heated square cavity filled with a fluid-saturated porous medium, Numer. Heat Transfer A. 53 (2008) 88–110 [CrossRef] [Google Scholar]
- A.J. Chamkha, A. Al-Mudhaf, Double-diffusive natural convection in inclined porous cavities with various aspect ratios and temperature-dependent heat source or sink, Heat Mass Transf. 44 (2008) 679–693 [CrossRef] [Google Scholar]
- T. Basak, S. Roy, S.K. Singh, I. Pop, Analysis of mixed convection in a lid-driven porous square cavity with linearly heated side wall(s), Int. J. Heat Mass Transf. 53 (2010) 1819–1840 [CrossRef] [Google Scholar]
- K. Khanafer, K. Vafai, M. Lightstone, Buoyancy-driven heat transfer enhancement in a two-dimensional enclosure utilizing nanofluids, Int. J. Heat Mass Transf. 46 (2003) 3639–3653 [CrossRef] [Google Scholar]
- R.Y. Jou, S.C. Tzeng, Numerical research of nature convective heat transfer enhancement filled with nanofluids in rectangular enclosures, Int. J. Heat Mass Transf. 33 (2006) 727–736 [Google Scholar]
- K.S. Hwang, J.H. Lee, S.P. Jang, Buoyancy-driven heat transfer of water-based Al2O3 nanofluids in a rectangular cavity, Int. J. Heat Mass Transf. 50 (2007) 4003–4010 [CrossRef] [Google Scholar]
- C.J. Ho, M.W. Chen, Z.W. Li, Numerical simulation of natural convection of nanofluid in a square enclosure: effects due to uncertainties of viscosity and thermal conductivity, Int. J. Heat Mass Transf. 51 (2008) 4506–4516 [CrossRef] [Google Scholar]
- M.A. Mansour, R.A. Mohamed, M.M. Abd-Elaziz, S.E. Ahmed, Numerical simulation of mixed convection flows in a square lid-driven cavity partially heated from below using nanofluid, Int. Commun. Heat Mass Transf. 37 (2010) 1504–1512 [CrossRef] [Google Scholar]
- M. Muthtamilselvan, P. Kandaswamy, J. Lee, Heat transfer enhancement of copper-water nanofluids in a lid-driven enclosure, Commun. Nonlinear Sci. Numer. Simul. 15 (2010) 1501–1510 [CrossRef] [MathSciNet] [Google Scholar]
- B. Ghasemi, S.M. Aminossadati, Mixed convection in a lid-driven triangular enclosure filled with nanofluids, Int. Commun. Heat Mass Transf. 37 (2010) 1142–1148 [CrossRef] [Google Scholar]
- D.A. Nield, A.V. Kuznetsov, The Cheng-Minkowycz problem for natural convective boundary-layer flow in a porous medium saturated by a nanofluid, Int. J. Heat Mass Transf. 52 (2009) 5792–5795 [Google Scholar]
- P. Cheng, W.J. Minkowycz, Free convection about a vertical flat plate embedded in a porous medium with application to heat transfer from a dike, J. Geophys. Res. 82 (1977) 2040–2044 [Google Scholar]
- A.V. Kuznetsov, D.A. Nield, The onset of double-diffusive nanofluid convection in a layer of a saturated porous medium, Transp. Porous Med. 85 (2010) 941–951 [CrossRef] [MathSciNet] [Google Scholar]
- S. Ahmad, I. Pop, Mixed convection boundary layer flow from a vertical flat plate embedded in a porous medium filled with nanofluids, Int. Commun. Heat Mass Transf. 37 (2010) 987–991 [CrossRef] [Google Scholar]
- N. Mittal, V. Manoj, D. Santhosh Kumar, A. Satheesh, Numerical simulation of mixed convection in a porous medium filled with water/Al2O3 nanofluid, Heat Trans. Asian Res. 42 (2013) 46–59 [CrossRef] [Google Scholar]
- M.T. Nguyen, A.M. Aly, S.W. Lee, Natural convection in a non-darcy porous cavity filled with Cu-water nanofluid using the characteristic-based split procedure in finite-element method, Numer. Heat Transf. A 67 (2015) 224–247 [CrossRef] [Google Scholar]
- C. Zhang, L. Zheng, X. Zhang, G. Chen, MHD flow and radiation heat transfer of nanofluids in porous media with variable surface heat flux and chemical reaction, Appl. Math. Modell. 39 (2015) 165–181 [CrossRef] [Google Scholar]
- J.C. Maxwell, A treatise on electricity and magnetism, second ed, Oxford University Press, Cambridge, 1904, pp. 435–441 [Google Scholar]
- W. Yu, S.U.S. Choi, The role of inter facial layers in the enhanced thermal conductivity of nanofluids: a renovated Maxwell model, J. Nano Res. 5 (2003) 167–171 [Google Scholar]
- S.V. Patankar, Numerical heat transfer and fluid flow, Hemisphere, Washington, DC, 1980 [Google Scholar]
- T. Hayase, J.A.C. Humphrey, R. Grief, A consistently formulated QUICK scheme for fast and stable convergence using finite-volume iterative procedures, J. Comput. Phys. 98 (1992) 108–118 [CrossRef] [Google Scholar]
- S. Roy, T. Basak, Finite element analysis of natural convection flows in a square cavity with non-uniformly heated wall(s), Int. J. Eng. Sci. 43 (2005) 668–680 [CrossRef] [Google Scholar]
- A. Arefmanesh, M. Mahmoodi, Effects of uncertainties of viscosity models for Al2O3-water nanofluid on mixed convection numerical simulations, Int. J. Therm. Sci. 50 (2011) 1706–1719 [CrossRef] [Google Scholar]
Cite this article as: M. Muthtamilselvan, S. Sureshkumar, Impact of aspect ratio on a nanofluid-saturated porous enclosure, Mechanics & Industry 18, 501 (2017)
All Tables
All Figures
 |
Fig. 1 A schematic view of the considered cavity in the present study. |
| In the text | |
 |
Fig. 2 (a) Mid-plane U-velocity for different mesh sizes at Ri = 100, Da = 10−2, ε = 0.4, χ = 0.06, and Ar = 0.5, (b) comparisons of the local Nusselt numbers with the results of Roy and Basak [26] and (c) the mid-plane velocity profiles of Mahmoodi et al. [27]. |
| In the text | |
 |
Fig. 3 Isotherms (left) and streamlines (right) for different Ri with ε = 0.4, Da = 10−2, Ar = 0.25, and χ = 0.06. |
| In the text | |
 |
Fig. 4 Isotherms (left) and streamlines (right) for different Ri with ε = 0.4, Da = 10−2, Ar = 0.5, and χ = 0.06. |
| In the text | |
 |
Fig. 5 Isotherms (left) and streamlines (right) for different Ri with ε = 0.4, Da = 10−2, Ar = 1, and χ = 0.06. |
| In the text | |
 |
Fig. 6 Isotherms (left) and streamlines (right) for different Ri with ε = 0.4, Da = 10−2, Ar = 2, and χ = 0.06. |
| In the text | |
 |
Fig. 7 U and V-velocity profiles at mid-plane of the cavity for different Ar and Ri with Da = 10−2, ε = 0.4, and χ = 0.06. |
| In the text | |
 |
Fig. 8 Local Nusselt numbers for different Ar and Ri with Da = 10−2, ε = 0.4, and χ = 0.06. |
| In the text | |
 |
Fig. 9 Isotherms (left) and streamlines (right) for different χ with ε = 0.4, Da = 10−2, Ri = 1, and Ar = 0.25. |
| In the text | |
 |
Fig. 10 Isotherms (left) and streamlines (right) for different χ with ε = 0.4, Da = 10−2, Ri = 1, and Ar = 0.5. |
| In the text | |
 |
Fig. 11 Isotherms (left) and streamlines (right) for different χ with ε = 0.4, Da = 10−2, Ri = 1, and Ar = 1. |
| In the text | |
 |
Fig. 12 Isotherms (left) and streamlines (right) for different χ with ε = 0.4, Da = 10−2, Ri = 1, and Ar = 2. |
| In the text | |
 |
Fig. 13 U and V-velocity profiles at mid-plane of the cavity for different Ar and χ with Da = 10−2, ε = 0.4, and Ri = 1. |
| In the text | |
 |
Fig. 14 Local Nusselt numbers for different Ar and χ with Da = 10−2, ε = 0.4, and Ri = 1. |
| In the text | |
 |
Fig. 15 Average Nusselt number. |
| In the text | |
 |
Fig. 16 Average Nusselt number. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


