| Issue |
Mechanics & Industry
Volume 18, Number 5, 2017
|
|
|---|---|---|
| Article Number | 506 | |
| Number of page(s) | 10 | |
| DOI | https://doi.org/10.1051/meca/2017020 | |
| Published online | 04 September 2017 | |
Regular Article
Optimization of a combined cooling heating and power generation system considering detailed thermodynamic design of the components: exergetic–economic–environmental optimization and evaluation
1
Aerospace Organization, MSc Graduated in Aerospace Engineering,
Tehran, Iran
2
Faculty of Economics, University of Sistan and Baluchestan,
Zahedan, Iran
3
Department of Mechanical Engineering, Najafabad Branch, Islamic Azad University,
Isfahan, Iran
4
Modern Manufacturing Technologies Research Center, Najafabad Branch, Islamic Azad University,
Najafabad, Iran
5
Research and Development Manager at FANSA Company,
Tehran, Iran
* e-mail: m.jamali@pmc.iaun.ac.ir
Received:
2
April
2016
Accepted:
16
March
2017
This research paper deals with a detailed design and optimization of a combined cooling, heating and power plant. This is a detailed fundamental approach to other optimizations and performance evaluation such as optimizing the operational strategy. Different scenarios are introduced and optimized. In addition, influences of prime mover size (e.g. produced power), interest rate and fuel cost on the plant optimum design are studied. Internal rate of return and net present value of the plant are calculated and used to compare the scenarios besides exergy efficiency and carbon dioxide emission. Results show that economic factors affect the optimum cycle thermodynamics greatly. Efficiencies, heat and cooling capacities and fuel flow rates at optimum design point vary significantly by economic factors and are correlated to the plant size.
Key words: CCHP / exergy / plant economy / optimization / environmental impacts
© AFM, EDP Sciences 2017
1 Introduction
In recent years, economy is not the only matter, built environment is important too. Numerous studies have been carried out to reduce the greenhouse gas emissions and there have been several efforts worldwide to come up with plans and strategies for global warming mitigation. Nowadays, environmental impact of a plant is a design consideration beside the plants' economy. Furthermore, due to energy resource shortages, systems are designed to utilize the energy sources as efficiently as possible. Economy, environmental impact and sustainability of energy resources are the basic criteria for any energy system. With the advent of the exergy definition, exergy efficiency has become popular since it has a close relation with sustainability. Furthermore, because exergy evaluates the exact value of the extractable work from a stream or resource, it is more suitable for economic evaluation and analysis. Hence, the exergy–economic–environmental assessment and modeling approach is an acceptable method for analyzing and designing the energy systems.
Exergy efficiency stands for energy sources management but is linked with the economy of the plant and has a direct relationship with environmental emission. Therefore, it is always subjected to optimization. Other objectives are cost of the plant and emission.
Nowadays, carbon taxes and emission cost are evaluated and implemented in plant cost considerations. Other emissions such as NOx, SOx and CO, which are classified as toxic or hazard gases, have their own costs and taxes as well. To evaluate the exact plant cost these issues must add to the total cost of the plant.
Optimization approaches for thermal systems regarding the objectives and algorithms can be categorized as follows:
-
optimizing the sizing and operational strategy of the plant;
-
optimizing the sizing and operational strategy considering the off design performance;
-
optimizing the plant considering the detailed design of the components and cycles.
In the first case a rough estimation of the modules such as microturbine using their bulk performance characteristics is used. For example, a microturbine can be modeled using its efficiency and output power or flow rates. An adsorption chiller can be modeled with its COP and required capacity.
To have a more realistic model off design, the operation of the plant can be considered as well. However, systems are modeled as bulk modules such as the first approach.
Finally, effects of detailed design parameters of each component and submodules on the optimum solution are evaluated using the final approach.
Combined cooling, heating and power (CCHP) systems have been studied widely by many researches through exergy, energy, economy, configuration and optimization. However, most of the papers considered the optimal strategy and sizing of the plant. Kong et al. [1] discussed an optimal operation strategy for CCHP units considering the demand loads. They used a linear programming and their criterion for the optimization was the cost of energy. They came out with the result that for some operation hours the turbine should be stopped from working. Their objective function was the cost of the input energy to the system. They found the optimal operation strategy for a working plant. Mentioned decision variables were turbine load fraction and exhaust gas splitting factor.
Fumo et al. [2] optimized the operation strategy for the environmental issues. They proposed an emission strategy and compared the plant emission with pervious operation strategy. They characterized the CCHP according to the capacity of the power generation unit. They compared CCHP emission with a reference building with separate heating and cooling systems. Their study resulted in a strategy plan for a designed CCHP unit, which reduced the emission by controlling the power generation unit power.
Wang et al. [3] optimized capacity and operation strategy for a CCHP unit with three objectives. Primary energy saving, total cost saving and emission are the objectives. They modeled the system as bulk modules with efficiency and COP parameters. They also carried out a sensitivity analysis for gas price and electricity price effect on optimized methodology.
Kong et al. [4] studied the energy management in CCHP and optimized its operation plan. Cost of energy was the objective of the optimization and a nonlinear programming method was used for optimization.
Mago and Chamra [5] optimized a CCHP system. They focused on the operation strategy and modeled the main components as block box and energy flows are considered. They proposed a hybrid thermal electrical load following and defined an objective function, which is a combination of the cost, emission and energy consumption. They showed that hybrid model can result in a more optimized system than electrical or thermal load following approach.
Cho et al. [6] optimized performance and operational strategy of a CCHP system based on cost, energy consumption and carbon dioxide emission. They studied different systems located in different cities. They considered three separate optimization objectives include of energy consumption, carbon emission and operational cost and studied the effects of them on other parameters.
Abdollahi et al. [7] provide an optimization approach for CCHP based on the system economy, environmental impact and exergetic performance. Micro gas turbine, chiller and heat recovery unit are all modeled using COP or efficiencies. Purchase cost of the objects evaluated as functions of their capacity and environmental costs is considered too. A multi-objective genetic algorithm was used to optimize three objective functions simultaneously. Microturbine and adsorption chiller capacities were considered as objective functions and optimization was carried out according to electrical, heating and cooling demand graphs. A detailed risk and economic analysis was used to investigate the profitability of the plan.
In the mentioned studies, optimization of the CCHP has been carried out based on the bulk models and operational strategy. Detailed modeling and optimization of CCHP and multigeneration plants have been carried out by Ahmadi et al. [8,9]. They modeled each component of the plant and considered exergy efficiency and cost flow as objective functions. Sophisticated cost modeling in their approach gives an inside through the cost flows in addition to exergy flows. Despite their very detailed and comprehensive modeling, the total cost of the plant is the only economic measure in their works and the environmental impacts are not considered. In this study, the detailed design of the cycle and its components and their effects on the exergy efficiency, cost and environmental aspects of the plant are considered. For the fundamental characteristics of microturbines, they are usually considered the first option as the prime mover. However, a complete study of trigeneration plant prime movers is carried out by Al-Sulaiman et al. [10]. Adsorption chillers can be single or multi-effect systems depending on the available heat, cooling demand and cost considerations [11]. Here, for simplicity, a single effect adsorption chiller is used beside a gas turbine and a heat recovery steam generator. In addition to optimization, a detailed economic study of the plant is carried out based on the internal rate of return (IRR) and net present value (NPV) to show the sensitivity of results on the local parameters such as fuel cost and interest rate. Furthermore, size of plant, which is specified with the size of prime mover (gas turbine), is varied as well and its influence on the optimum results are studied. The main objective of this research is to present a method for an optimum design of a plant, which covers the detailed design parameters of the components and includes the main objectives of optimization such as cost, emission and efficiency. Various scenarios are defined and each scenario is optimized using multi-objective optimization algorithm. Results are compared based on the economic criteria and the best conditions are presented.
The highlights of the present work are as follows:
-
detailed modeling of the components based on the first and second law analyses;
-
economic evaluation of the component costs using the cost function, which include effects of thermal design;
-
using multi-objective optimization for each scenario, 8 scenarios are subjected to optimization;
-
detailed cost and benefit evaluation for plant is presented;
-
different economic measures such as NPV and IRR are used to compare the performance of the different scenarios in addition to exergy efficiency and carbon emission.
The size and economy of the plant is dependent on the demands. Therefore, the optimization of CCHP is case dependent and the electrical, heating and cooling demands are needed for the case. So the first step in the procedure is defining the case study.
2 Case study specification
In order to provide a method for a practical example, at first, specifications of the studied complex is presented. Existing buildings in Foxhill have been selected for this purpose. This collection includes 288 apartment units in the city of Austin. Currently, each unit includes central heating and cooling system, which has been constructed in 2010.1,2
According to reference [12], average energy consumption in Texas buildings is as shown in Table 1.
The data are calculated as energy consumption per square foot in a month. According to the Foxhill complex data,1,2 charts of average monthly energy consumption calculated and showed in Figure 1.
Average energy demands for residential buildings in Texas (1000 Btu ft−2).
 |
Fig. 1 Estimated load demands of the fox hill complex (kW). |
3 Case study description
Studied cycle is illustrated in Figure 2. This cycle comprises of a turbine, a heat recovery steam generator (HRSG) and an absorption chiller. Stream of turbine exhaust gases flow into HRSG, which provide heat energy for steam generation. Generated steam enters absorption chiller and is assumed to exit at saturation condition. Resulted hot water is utilized for heating and cooled to 40 °C. Heating and cooling strategy follows the buldings' thermal and chilling loads respectively.
During seasons when cooling load is low, main portion of the steam flow is guided toward heating unit. Therefore, during cold seasons, generated steam is consumed for heating, and during hot seasons, it is consumed for cooling. Based on gas turbine cycle output power and economical parameters, the following three different scenarios are considered:
-
gas turbine unit work generation equals electricity base load. Under this condition, it is assumed that cooling and heating energy demand of the units is supplied via electrical chiller with COP of 3 and boiler with an efficiency of 85%, respectively;
-
generated work equals maximum electrical load including electrical energy demand for cooling purpose. In this situation, heating load is supplied by a boiler with an efficiency of 85%. In this scenario it is possible to sell electricity to the network;
-
third scenario is as same as the 2nd one with a difference that excess electrical energy is sold to the network.
Various scenarios have been studied. Furthermore, analysis of fuel price and interest rate have been performed in relation with economical profit and payback period (PBP) of investment, which can reveal impact of energy policies on the feasibility of discussed plans.
For each scenario, optimization is implemented via genetic algorithm considering costs and environmental impact. At the end, comparison of different scenarios is done.
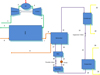 |
Fig. 2 Shematic of the proposed cycle. |
4 Thermodynamic modeling and exergy analysis
Modeling and exergy–economic analysis is performed via modeling each component to investigate the effect of different parameters on cost and efficiency by means of cost function updated through comparison of available prices.
Gas turbine cycle model is achieved via mathematical model introduced in reference [13]. Furthermore, absorption chiller and heat recovery boiler are modeled via relations presented in reference [14].
Exergy efficiency as one of the target functions is as follows:
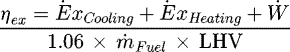 (1)
where
(1)
where 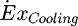 and
and  are the exergy associated with cooling and heating, respectively, which can be expressed as follows:
are the exergy associated with cooling and heating, respectively, which can be expressed as follows:
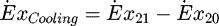 (2)
(2)
 (3)
(3)
5 Environmental impact assessment
Consideration of economic effects and evaluation of pollutant emissions are implemented via introduced methods in reference [13]. Economic calculations of pollutants' cost are done according to Ehyaei et al. [15]. In addition, carbon dioxide generation per unit of exergy is calculated.
6 Economic analysis
Economic analysis of the plan begins with calculation of investment cost function and conversion to current cost during operation life of the cycle based on following relations:
 (4)
Fuel cost is also considered as current cost. Installation and operation costs are considered as initial investment. Therefore, total cost is obtained through following relations:
(4)
Fuel cost is also considered as current cost. Installation and operation costs are considered as initial investment. Therefore, total cost is obtained through following relations:
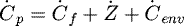 (5)Income calculation in each case is different as follows:
(5)Income calculation in each case is different as follows:
-
In the 1st scenario, electrical energy demand of the unit, and also in a portion of the cooling and heating load, is produced by the unit. Therefore, relevant cost reduction is as follows:
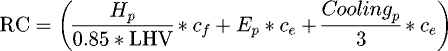 (6)
(6)
 (7)
in which figures of 3 and 0.85 represent chiller performance and boiler efficiency, respectively. RC is the monthly averaged cost reduction. In fact such a cost reduction is the income gained by the investment. Since investment and fuel costs are considered as current cost, monthly profit is obtained via following relation:
(7)
in which figures of 3 and 0.85 represent chiller performance and boiler efficiency, respectively. RC is the monthly averaged cost reduction. In fact such a cost reduction is the income gained by the investment. Since investment and fuel costs are considered as current cost, monthly profit is obtained via following relation:
-
in 2nd scenario, calculations are the same as previous ones. If generated cooling or heating is more than buildings load, Coolingp or Hp is assumed equal to building cooling or heating load.
-
in 3rd scenario, excess generated electricity is sold to the network. Obviously cost reduction and profits are different as follows:
 (8)
(8)
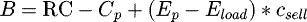 (9)
For each of the discussed items, sensitivity analysis is performed and effects of natural gas and electricity prices as well as interest rate on the economic feasibility of the plan are studied.
(9)
For each of the discussed items, sensitivity analysis is performed and effects of natural gas and electricity prices as well as interest rate on the economic feasibility of the plan are studied.
Preceding the evaluation of yearly profit, internal interest rate and NPV are studied to investigate the changes in return of project.
NPV is defined as follows:
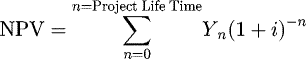 (10)
in which, Yn is the net cash flow at the end of n time interval.
(10)
in which, Yn is the net cash flow at the end of n time interval.
The IRR method seeks to avoid the arbitrary choice of an interest rate; instead, it calculates an interest rate, initially unknown, that is internal to the project. The procedure is to determine the interest rate i*, called the IRR, that makes the NPV of an investment zero. That is,
 A project is selected if the calculated IRR is greater than the minimum acceptable rate of return. The projects with the highest internal rates of return are given the highest preference among various alternatives.
A project is selected if the calculated IRR is greater than the minimum acceptable rate of return. The projects with the highest internal rates of return are given the highest preference among various alternatives.
Mathematically, the PBP is defined by the following relation:
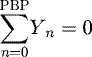 (12)
where Yn is the projects’ net cash flow in the Zth year.
(12)
where Yn is the projects’ net cash flow in the Zth year.
7 Optimization procedure
Design procedure begins with the determination of characteristics such as building load curve, costs and prices. Economic criteria including interest rate, natural gas and electricity price play critical role. In the present research study, calculations are performed based on 2012 data of Austin in Texas. After the selection of basic parameters, building thermodynamic deign is performed considering following key points:
-
electrical energy consumption of the building is a specific amount for a year whereas cooling and heating loads vary during different seasons;
-
electrical energy consumption of the building is a specific amount for a year whereas cooling and heating loads vary during different seasons.
Gas turbine cycle is considered as the base criteria and generated work as the input data of the design procedure. Decision variables employed during design and optimization process are introduced in Table 2.
Exergy efficiency and pollutant emission are defined as target functions. Then for each scenario of analysis, interest rate and Cost of energy carriers are optimized via genetic algorithm as a multi-purpose method. Based on obtained optimized plan, amount of generated cooling and heating and also current cost are calculated and then economic calculations are carried out. Finally, selection of optimum variables will be possible regarding calculated values. The optimization flow diagram is shown in Figure 3.
List of decision variables for optimization.
 |
Fig. 3 Flow diagram of the optimization and selection procedure. |
8 Results and discussion
This work presents the cooling and heating production, cost and efficiency for a variety of situations and scenarios with different interest rate, fuel price and produced work. As discussed, amount of generated cooling and heating varies according to demand loads; these changes in situation are considered via applying coefficient of operation. Cooling and heating loads equal maximum cooling generation capacity and minimum level of heating generation of the unit under optimal conditions. Balance between two outputs is dictated by building load. The portion of the extra cooling, which is consumed for heating, is calculated by means of COP.
Different scenarios are defined considering various interest rates, fuel price, gas turbine power output and electricity selling price. Table 3 shows different scenarios and corresponding values for mentioned parameters.
IRR is plotted versus fuel price in Figure 4. As is shown, an increase in fuel price reduces the project return. At lower values of the fuel price, IRR is higher than 15%, which is an acceptable value for return on investment. With values higher than 0.07 $ GJ−1, IRR reduces to the values under 0.15%, and when the real end user price of fuel is assumed, which is about 0.09 $ GJ−1, only options with excess electricity selling capability have return ratios more than interest rate. Therefore, one may conclude from Figure 4 that if real fuel price is accounted, electricity selling price to the network must be about it purchasing price from the network.
Corresponding to IRR, PBP is another economic measure. As is presented, PBP for the fuel costs below 0.07 is a reasonable value less than or about 5 years. However, when the price increases to the real end consumer price, only the last option with electricity selling price of about 0.09 $ GJ−1 is viable. Projects with PBPs above 5 or at most 6 years are not economically attractive in a competitive market. This trend is shown in Figure 5.
The next but not a lesser important economic measure is the well known NPV or NPV of the project. A project with a positive NPV value is an economically feasible one. The same trend is followed with NPV measure (Fig. 6). NPV of about the capital investment is commonly accepted. However, NPV is not as accurate a measure as IRR.
Discounted net cash flow is the first economic measure. It is simply the net cash flow of the system including the investment cost. To consider the capital investment as a cash flow, investment is discounted over 20 years of operation lifetime. As is shown in Figure 7, when net cash flow is positive, the project is economically feasible since net income is positive. Net income for options without electricity selling capability is negative, which is in line with the previous results.
NPV shows whether a project is economically feasible (positive NPV) or not feasible (negative NPV). It does not tell how much this project could be efficient. PBP is a simple measure, which does not include the interest rate; therefore, it is not a precise measure. As one may find out by comparing Figures 5 and 6, projects with negative NPVs also have PBPs lower than project lifetime, which shows the inaccuracy of PBP method. Among the measures, IRR is the most accurate and clear one. It shows the economic efficiency of the project in terms of rate of return.
To make CCHPs competitive in energy markets, not only the interest rate and fuel prices should be low enough but also the capability of selling excess electricity to the network should be available. Buildings due to uneven heating, cooling and electrical loads always produce extra energy in some hours of the day or year. Here, for simplicity, only monthly variations are included, but results show that how much this variable load characteristic is important in plant designing and economy. Figure 8 presents the effect of electricity selling price on the economic performance of the plant.
As is shown so far, turbine output power of 700 kW is more economic than 440 kW. There are two main reasons for this. The first is, excess electricity can be sold to the network, which increases net income. The second and the more important reason is that 700 kW gas turbine, more heat energy at turbine exhaust is available. This means that cooling and heating loads can be almost covered by the CCHP system and supplementary boiler fuel. Also the electricity for excess cooling demand are reduced significantly. This results in higher energy and cost saving (income). Figure 9 shows the variations of heating and cooling produced for different cases in Table 3. Cooling and heating production rates for the 700 kW case are significantly higher than the 440 kW case.
Effect of current expenditures on the fixed costs (investment costs) is clear while comparing cases 6 through 8 in Figure 10. As fuel price is rising, current costs are increasing and this forces the capital investment to reach lower values. However, lower investment costs mean lower efficiencies since cheaper technology is implemented. Lower efficiencies mean higher fuel flow rate and consequently higher costs. Therefore, if fuel price reaches higher values, higher technologies must be implemented. In this case, total cost of the plant or cost level of the plant is rising (case 8). Efficiency trends of the cycle and COP of adsorption chiller is shown in Figure 11. Results for efficiencies are in line with our discussion on Figure 9.
Effect of interest rate is to amplify the capital cost. Higher interest rates increase the capital cost rates. Higher investment rate forces the investment cost to decrease significantly, which means lower technology price. Since the cost is reducing significantly, IRR rises. Further increase in interest rate results in lower IRR, since further decrease in technology cost is impossible due to increase in fuel flow rate and cost rate. In this case, total cost of the plant is rising, which reduces the IRR. The trend is illustrated in Figure 12.
Different scenarios according to economic parameters.
 |
Fig. 4 Effect of fuel price on the IRR of the plant. |
 |
Fig. 5 Effect of fuel price on the payback period of the plant. |
 |
Fig. 6 Effect of fuel price on the NPV of the plant. |
 |
Fig. 7 Effect of fuel price on the net discounted cash flow. |
 |
Fig. 8 Effect of electricity selling price on the IRR of the plant. |
 |
Fig. 9 Cooling and heating produced in different cases. |
 |
Fig. 10 Capital and fuel cost of the plant. Capital cost in million $ and fuel cost rate in $ h−1. |
 |
Fig. 11 COP and efficiency of the plant for different cases. |
 |
Fig. 12 Effects of interest rate on the IRR. |
9 Conclusion
Effect of various economic factors on the design optimization of a CCHP system was investigated. Each economic data set corresponded to an optimum solution. Environmental, current and investment costs are included in economic objective function. Effects of interest rate, electricity selling price, fuel price, and output power were studied and discussed. Economic measures such as net discounted cash flow rate, PBP, NPV and IRR were used to evaluate the economic performance of the optimum designed plants.
Results show that 700 kW generation unit is more economically feasible than the 440 kW case, since higher exhaust gas flow rates of the gas turbine lead to higher cooling and heating production, which can cover the demands of the buildings. Another reason is that excess electricity can be sold to the network, which increases the income significantly.
Optimum current and fixed costs are affected by the economic factors. Interest rate increases share of fixed cost, and fuel price causes the current costs to rise notably. While one cost rate is rising due to an economic factor variation, optimization method brings the total cost to a new equilibrium point.
Design of the cycle as shown in this study is very sensitive to the economic factors. Also, results show that not only fuel price reduction and interest rates must be kept significantly low, but also the plant should be able to sell its excess electricity produced to the energy network. This capability will make the CCHPs more competitive in energy markets.
References
- X.Q. Kong, R.Z. Wang, X.H. Huang, Energy optimization model for a CCHP system with available gas turbines, Appl. Therm. Eng. 25 (2005) 377–391 [CrossRef] [Google Scholar]
- N. Fumo, P.J. Mago, L.M. Chamra, Emission operational strategy for combined cooling, heating, and power systems, Appl. Energy 86 (2009) 2344–2350 [Google Scholar]
- J.-J. Wang, Y.-Y. Jing, C.-F. Zhang, Optimization of capacity and operation for CCHP system by genetic algorithm, Appl. Energy 87 (2010) 1325–1335 [CrossRef] [Google Scholar]
- X.Q. Kong, R.Z. Wang, Y. Li, X.H. Huang, Optimal operation of a micro-combined cooling, heating and power system driven by a gas engine, Energy Convers. Manag. 50 (2009) 530–538 [CrossRef] [Google Scholar]
- P.J. Mago, L.M. Chamra, Analysis and optimization of CCHP systems based on energy, economical, and environmental considerations, Energy Build. 41 (2009) 1099–1106 [Google Scholar]
- H. Cho, P.J. Mago, R. Luck, L.M. Chamra, Evaluation of CCHP systems performance based on operational cost, primary energy consumption, and carbon dioxide emission by utilizing an optimal operation scheme, Appl. Energy 86 (2009) 2540–2549 [CrossRef] [Google Scholar]
- G. Abdollahi, M. Meratizaman, Multi-objective approach in thermoenvironomic optimization of a small-scale distributed CCHP system with risk analysis, Energy Build. 43 (2011) 3144–3153 [CrossRef] [Google Scholar]
- H. Ghaebi, M.H. Saidi, P. Ahmadi, Exergoeconomic optimization of a trigeneration system for heating, cooling and power production purpose based on TRR method and using evolutionary algorithm, Appl. Therm. Eng. 36 (2012) 113–125 [CrossRef] [Google Scholar]
- P. Ahmadi, I. Dincer, M.A. Rosen, Thermodynamic modeling and multi-objective evolutionary-based optimization of a new multigeneration energy system, Energy Convers. Manag. 76 (2013) 282–300 [Google Scholar]
- F.A. Al-Sulaiman, F. Hamdullahpur, I. Dincer, Trigeneration: a comprehensive review based on prime movers, Int. J. Energy Res. 35 (2011) 233–258 [CrossRef] [Google Scholar]
- D.W. Wu, R.Z. Wang, Combined cooling, heating and power: a review, Progr. Energy Combust Sci. 32 (2006) 459–495 [Google Scholar]
- Methodology to perform a non-conventional evaluation of Cooling, Heating, and Power (CHP) systems, Southeastern Regional Combined Cooling Heating and Power Application Center, 2007 [Google Scholar]
- H. Barzegar Avval, P. Ahmadi, A.R. Ghaffarizadeh, M.H. Saidi, Thermo-economic-environmental multiobjective optimization of a gas turbine power plant with preheater using evolutionary algorithm, Int. J. Energy Res. 35 (2010) 389–403 [CrossRef] [Google Scholar]
- H. Ghaebi, M. Amidpour, S. Karimkashi, O. Rezayan, Energy, exergy and thermoeconomic analysis of a combined cooling, heating and power (CCHP) system with gas turbine prime mover, Int. J. Energy Res. 35 (2011) 697–709 [CrossRef] [Google Scholar]
- M.A. Ehyaei, A. Mozafari, M.H. Alibiglou, Exergy, economic & environmental (3E) analysis of inlet fogging for gas turbine power plant, Energy 36 (2011) 6851–6861 [Google Scholar]
Cite this article as: A. Abdolkarimi, M. Karabi, M.J. Ghahderijani, H. Karabi, Optimization of a combined cooling heating and power generation system considering detailed thermodynamic design of the components: exergetic–economic–environmental optimization and evaluation, Mechanics & Industry 18, 506 (2017)
All Tables
All Figures
 |
Fig. 1 Estimated load demands of the fox hill complex (kW). |
| In the text | |
 |
Fig. 2 Shematic of the proposed cycle. |
| In the text | |
 |
Fig. 3 Flow diagram of the optimization and selection procedure. |
| In the text | |
 |
Fig. 4 Effect of fuel price on the IRR of the plant. |
| In the text | |
 |
Fig. 5 Effect of fuel price on the payback period of the plant. |
| In the text | |
 |
Fig. 6 Effect of fuel price on the NPV of the plant. |
| In the text | |
 |
Fig. 7 Effect of fuel price on the net discounted cash flow. |
| In the text | |
 |
Fig. 8 Effect of electricity selling price on the IRR of the plant. |
| In the text | |
 |
Fig. 9 Cooling and heating produced in different cases. |
| In the text | |
 |
Fig. 10 Capital and fuel cost of the plant. Capital cost in million $ and fuel cost rate in $ h−1. |
| In the text | |
 |
Fig. 11 COP and efficiency of the plant for different cases. |
| In the text | |
 |
Fig. 12 Effects of interest rate on the IRR. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


