| Issue |
Mechanics & Industry
Volume 18, Number 8, 2017
Experimental Vibration Analysis
|
|
|---|---|---|
| Article Number | 803 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/meca/2017043 | |
| Published online | 21 March 2018 | |
Regular Article
Structural impact response for assessing railway vibration induced on buildings
1
University of Mons − UMONS, Faculty of Engineering, Department of Theoretical Mechanics, Dynamics and Vibrations,
Place du Parc 20,
7000
Mons, Belgium
2
National Technical University of Athens − NTUA, School of Civil Engineering, Laboratory for Earthquake Engineering,
Heroon Polytechneiou street 9,
15700
Athens, Greece
3
University of Thessaly, Department of Civil Engineering, Laboratory of Transportation Environmental Acoustics − L.T.E.A.,
Pedion Areos,
38334
Volos, Greece
* e-mail: georges.kouroussis@umons.ac.be
Received:
12
December
2016
Accepted:
6
November
2017
Over the syears, the rapid growth in railway infrastructure has led to numerous environmental challenges. One such significant issue, particularly in urban areas, is ground-borne vibration. A common source of ground-borne vibration is caused by local defects (e.g. rail joints, switches, turnouts, etc.) that generate large amplitude excitations at isolated locations. Modelling these excitation sources is particularly challenging and requires the use of complex and extensive computational efforts. For some situations, the use of experiments and measured data offers a rapid way to estimate the effect of such defects and to evaluate the railway vibration levels using a scoping approach. In this paper, the problem of railway-induced ground vibrations is presented along with experimental studies to assess the ground vibration and ground borne noise levels, with a particular focus on the structural response of sensitive buildings. The behaviour of particular building foundations is evaluated through experimental data collected in Brussels Region, by presenting the expected frequency responses for various types of buildings, taking into account both the soil-structure interaction and the tramway track response. A second study is dedicated to the Athens metro, where transmissibility functions are used to analyse the effect of various Athenian building face to metro network trough comprehensive measurement campaigns. This allows the verification of appropriate vibration mitigation measures. These benchmark applications based on experimental results have been proved to be efficient to treat a complex problem encountered in practice in urban areas, where the urban rail network interacts with important local defects and where the rise of railway ground vibration problems has clearly been identified.
Key words: Ground vibration / impact force / measurement on building / vibration assessment / turnout / rail joint / Brussels tram / Athens metro
© AFM, EDP Sciences 2017
1 Introduction
Railway networks represent an interesting modal transfer and they significantly alleviate traffic congestion and pollution. However, railways are subject to some drawbacks, particularly problems related to noise and vibration. Considerable efforts have been made in order to reduce the generated vibrations in the vehicle, improving the passengers' comfort, but the ground vibration problem must also be solved [1]. In a growing number of situations, the influence of vibrations on structural damage in buildings and on people inside buildings can no longer be neglected [2]. As pointed out in [3], large financial support is needed to fix vibration problems across the countries network (e.g. 1200 million euros were necessary for reducing the excessive levels of vibration for Switzerland's national railway). A major issue facing railway vibrations is that rail infrastructure continues to grow globally [4]. Numerous environmental issues are therefore effective, including ground-borne vibration in urban areas, and extensive efforts need to be placed on predicting accurate vibration levels and on understanding human perception of vibration [5].
A considerable amount of studies into railway-induced ground vibrations have been undertaken, focusing on the effect of high-speed trains on the environment. This was motivated by a physical phenomenon which appears when the vehicle speed is close to the Rayleigh ground wave speed (supercritical phenomenon). The latter depends on the soil flexibility and may be close to the vehicle speed for conventional high-speed lines [6]. Despite the large vibration levels generated by these lines which are underlain by soft soils, the distance d between the track and neighbouring structures is relatively large and the vibration attenuates rapidly. In the case of railway traffic, the attenuation is associated with a power law of the form d−q, where q lies between 0.5 and 1.1, depending on the soil configuration [7]. In urban area, local defects constitute a significant source of dynamic excitation on railway tracks and induce a different attenuation law, coupled to a soil medium relatively heterogeneous and complex. Moreover, the presence of local defects induces elevated localised vibrations (dynamic effect) [8]. Recently, some specific studies focused on the vehicle effects (RIVAS project [9], CarboVibes project [10]). However, it is evident that urban areas have not been intensively studied, despite the fact that more complaints were received in urban areas compared to other train networks. The most challenging aspect is to develop models or prediction tools dealing with these areas, since there is a distinct lack of studies on analysing the effect of local defects (e.g. switches, rail joints, etc.) on ground vibration in urban environments.
This negative environmental side effect of railways is mainly categorised into two major types, the ground vibrations in the areas around the rails which are induced by train passage and the noises produced by the wheels rolling over the rails. Recent breakthroughs focused on the interaction between the vehicle and its neighbourhood by considering and analysing the effect of the train dynamics on the track and soil response [11]. In the early stages of railway network design, vibrations are often evaluated using empirical methods such as the detailed vibration assessment procedure of the Federal Railroad Administration of the U.S. Department of Transportation [12] or as the empirical calculation procedure proposed by Crispino and D'Apuzzo for heritage buildings [13]. Large-scale evaluation methods are also of interest, offering a rapid way to assess the implementation and the verification of the mitigation measures for the protection of building cultural heritage [14]. Overloading the rail network causes economic losses because the existing lines are unable to withstand certain traffic loads and the more traffic there is the more the rails are worn down [15]. The replacement of the existing tracks with new ones, which will be able to carry the required traffic load, is generally not being considered for economic reasons. On the contrary, for old tracks, it is more sufficient to decrease the impact force that the train induces. Vogiatzis and Kouroussis studied floating slab track solutions which were then evaluated at crossover locations ensuring a complete ground-borne vibration attenuation [16]. Hybrid methods, combining experimental and numerical data, offer an efficient way to present a versatile tool to faithfully predict the vehicle/track interaction in urban cases. Auersch proposed to combine numerical ground wave models with experimental force spectra for a realistic prediction of railway-induced ground vibration [17]. Verbraken et al. calculated ground vibrations using analytical force densities and experimental line transfer mobilities, characterizing the transfer of vibrations and including the effect of the local geology on wave propagation [18]. Other scoping approaches are also available using a neural network approach coupled to a numerical model that predict vibration levels in terms of velocity decibels, taken into account the soil properties and multi-layered strata [19,20].
The main excitation source for both conventional and freight trains is the wheel/rail contact and it is associated with singular defects on both parts. Wheel flats, rail joints or turnouts are one of the most common local defects. Flats are mainly produced when the trains violently use the braking system and the wheel slides on the rail. Rail joints and turnouts are singular rail defects unavoidable due to rail networks design and often encountered in urban area. This kind of defect induces great periodic input forces on both the train and the track [21]. Railway local irregularities are a growing source of ground-borne vibration and the associated ground vibration levels are highly sensitive to defect height, length and shape [22].
The aim of this paper is to evaluate the ground-borne vibrations which are perceived by the neighbours residing close to the lines. The main originality lies on the use of in-situ test only in order to compare the dynamic amplification of each studied site. The fundamental assumption of point and line source excitations is discussed. Then a précis of the experimental determination of transfer mobilities between track and soil, including measurement technology and procedure, is given. In the next section, a review and collection of measured vibration data for the tramway of Brussels and the metro of Athens are given. The results will then be studied in order to figure out some useful conclusions.
2 Problem statement
The ground vibration near railway lines is caused by dynamic train loads, which depend on the nature of the interaction between the railway vehicle and the track. In the case of distributed irregularities along the track alignment, the vibration is mainly caused by the quasi-static track deflection, with amplification due to the dynamic interaction between the wheelsets and the rail. Due to the track invariance along the direction x, it is assumed that the effect of a wheelset j on a track/soil system is defined as
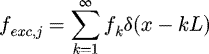 (1)
where fk is the force acting through the kth sleeper interface at each distance L regularly spacing the sleepers. The resulting vibrations at several distances from the track result from the summation of the effects of each force fk in the neighbourhood (Fig. 1a) and are often called line source vibration. In practice, the forces acting on sleepers far from the receptor have a negligible influence on the resulting vibration level, so as equation (1) becomes in practice
(1)
where fk is the force acting through the kth sleeper interface at each distance L regularly spacing the sleepers. The resulting vibrations at several distances from the track result from the summation of the effects of each force fk in the neighbourhood (Fig. 1a) and are often called line source vibration. In practice, the forces acting on sleepers far from the receptor have a negligible influence on the resulting vibration level, so as equation (1) becomes in practice
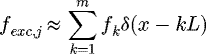 (2)which precludes the impact of forces outside a predefined distance range (recent numerical simulations showed that limited track part of 50–60 m length provides satisfactory results [23,24]).
(2)which precludes the impact of forces outside a predefined distance range (recent numerical simulations showed that limited track part of 50–60 m length provides satisfactory results [23,24]).
In the case of a local defect, the ground vibration near railway lines is the result of the interaction of the railway vehicle and the track when the train is running over an irregularity of the wheel or track. Although the case of singular defects in wheel surface is particular (like wheel flats inducing a series of periodic impacts as dynamic excitation and for which a strong wheel/rail coupling is necessary [8]), other singular defects on the rail can be seen as a single dynamic excitation on the wheel/rail defect contact point (Fig. 1b). In addition, if the vehicle train speed is low (light transit vehicles, like trams or metros, are characterized by a low speed and a relatively high density of singular rail surface defects), the dynamic track deflection mainly contributes to ground wave generation [25] and it is relatively reasonable to consider the single force acting on the wheel/rail defect contact point as the only contributor to railway vibration. Therefore,
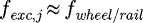 (3)
represents the force acting at the wheel/rail interface when a wheelset j is in contact with the local defect. Notice that the location of excitation may differ between equations (1) and (3).
(3)
represents the force acting at the wheel/rail interface when a wheelset j is in contact with the local defect. Notice that the location of excitation may differ between equations (1) and (3).
An accurate prediction of these vibrations can be performed by several numerical models, for high-speed trains [26–28] or for urban networks [29–31]. However, a significant computation time is needed for a complete vehicle/track/soil simulation and a vast section of vehicle, track and soil parameters are necessary. A scoping procedure can be preferable in some cases, as the technique developed by Nelson and Saurenman [32] for predicting ground borne noise and vibration caused by railway vehicles. The main focus of this tool is the estimation of ground-borne noise and vibration between 6.3 and 200 Hz in residential areas near at-grade and subway track. The problem is reduced to estimating ground surface vibration with the help of the line transfer mobility, defined as a function of the frequency f,
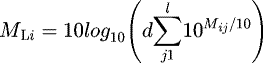 (4)
obtained by the superposition of l point transfer mobilities Mij between several points j (j : 1 ↦ l) of the rail, spaced of distance d, and the studied receptor response xi, and the force density LF obtained from tests [12] or numerical calculations [33]. The resulting vibration is calculated at distance yi from the track to predict the vibration velocity level
(4)
obtained by the superposition of l point transfer mobilities Mij between several points j (j : 1 ↦ l) of the rail, spaced of distance d, and the studied receptor response xi, and the force density LF obtained from tests [12] or numerical calculations [33]. The resulting vibration is calculated at distance yi from the track to predict the vibration velocity level
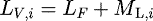 (5)often in one-third octave bands (for simplicity purposes).
(5)often in one-third octave bands (for simplicity purposes).
The basis of this method is the measurement of a single source transfer mobility function between various points i on a system. This function gives, as its name suggests, the transfer dynamic characteristics between two points of the system − the soil velocity response Xi (f) and the force Fj (f) acting at the soil surface − and yields soil dynamic information in the frequency domain [34]. A single source transfer mobility is theoretically defined by
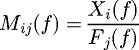 (6)
(6)
Regarding the aforementioned railway-induced ground vibration problem, it can be learned that the more the number of point transfer mobilities is important, the more the calculation expression given by equation (4) can assess the problem of a distributed irregularities along the track and/or the effect of a high-speed train (ideally, m = l and d = L). However, if the study is dedicated to low speed and to the dynamic effect of local defects, one point transfer mobility (or a small number of point transfer mobilities) remains sufficient to evaluate the vibratory effect of the ground wave propagation. This second case is truly applicable to urban environment.
 |
Fig. 1 Setup for vibration propagation tests: a) for distributed source and b) for local source of excitation. |
3 Experimental setup
In order to generate the transfer mobility function Mij between two points i and j, simultaneous analyses must be performed on data signals representing the input force applied at one point j of the system and the system response motion measured at a different point i
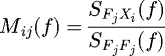 (7)
where auto-spectrum of the excitation
(7)
where auto-spectrum of the excitation  and cross-spectrum of excitation and response
and cross-spectrum of excitation and response 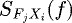 are defined as
are defined as
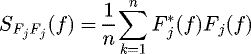 (8)
(8)
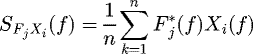 (9)
(9)
In addition, the causal and linear relationship between the output and input can be physically reflected by the coherence function, defined as
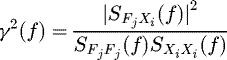 (10)
where intervenes the auto-spectrum of the response
(10)
where intervenes the auto-spectrum of the response 
Careful consideration needs to be given to noise and to leakage in the Fourier transform, since poor coherence is indicative of poor signal-to-noise ratio, measurement errors, non-linearity or time-variant behaviour of the structure, or a combination of them. Depending upon the type of measurement used to detect the response motion, the soil velocity response Xi (f) may be calculated as one derivative or one integration. Robust signal processing techniques are therefore required to avoid non-physical signals associated with the integration constant or the derivative gradient inherent to the original noisy signal and to the sampling rate.
3.2 Excitators
The forcing function may be applied to the structure by various methods. One common way to excite structures is by use of a sledge hammer or an impacter.
A dynamic impulse hammer with embedded force sensor is an efficient excitator, easy to use and very portable. It must however excite the structure with constant force over the frequency range of interest. Moreover, the weight of the hammer and the number of impacts require physical requirements from the operator and a reliable series of impacts could not necessary be obtained [34].
An alternative is the use of a mechanical exciter in the form of a drop hammer impactor. In the present work, a falling mass machine (Fig. 2) was dedicated to some tests where portability was not a necessary constraint. It consists of a steel frame serving as a guidance support for a falling mass. The latter is constituted by several heavy masses of 12.5 kg each one and an elastomer support allowing a filtering of the desired frequency range. The total mass can reach up to 52 kg and be launched from a maximum height of 1.5 m. A mechanical winch is used with a handle that makes raising the mass easier and a seat belt buckle serves as actuator. An accelerometer is expected to be placed on top of the mass, measuring the mass acceleration (and the excitation force by multiplying the measured acceleration by the mass). A short analytical calculation proved that, for a nominal height of 1 m, the expected duration of the impact is 2.2 ms with a maximum acceleration of 200 g (corresponding to a maximum force of 10 tonnes), covering a frequency range up to 100 Hz.
This second excitation device has the advantage of applying not only a calibrated force pulse to the rail but also one of constant shape and frequency content, as illustrated in Figure 3 demonstrating the repeatability of the excitation. To avoid the harmful effect of mass rebounds, dedicated signal processings were be applied to the measured traces, like rectangular and exponential windowing or homomorphic filtering [35], for removing the undesired parts of the signals.
 |
Fig. 2 Falling mass machine. |
 |
Fig. 3 Example of 10 measured impact force samples with the falling mass machine. |
3.3 Receptors
Several accelerometers and/or geophones can be placed along a profile perpendicular to the track, measuring the vertical soil response (Fig. 4). The distance from the track is identified from the edge of the closest rail. A first accelerometer could be placed close to the track (tram site edge) and the other at distant points of interest (sensitive building, foundation walls of dwelling, etc.). If the number of sensors is sufficient, the attenuation of ground vibrations with the distance can be calculated as well as the decay of the frequency content (soil filtering) and the scattering effect of the soil heterogeneity.
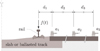 |
Fig. 4 Experimental setup and location of the sensors. |
4 Case 1: data collected on the tramway network of Brussels
Experimental data from a total of 14 test locations, designated from site 1 to site 14, across the Brussels Region, were examined (Fig. 5). All sites consisted of slab and ballasted tracks and cover the most tramway networks in the area of Brussels. Further considerations included:
-
The falling mass machine described in Section 3.1 was used for exciting the rail. An integrated electronic piezoelectric (IEPE) sensor was fixed on top of the mass for measuring the impact force. Piezoelectric accelerometers were fixed on structures by cementing them to the test surface. As vibration velocities are expected to be analysed in this study, acceleration time histories were converted into their equivalent velocity components. Analogue signal conditioners with amplifier were used for this purpose.
-
For all sites, vertical component vibration signals were recorded. At least, one sensor was placed at the tram site edge and one sensor at the building foundation. Except for sites 2 and 9, an additional sensor was also fixed on the edge of the sidewalk.
-
Although datasets were recorded at several different locations, a particular attention was paid to keep the same measurement location distances when possible.
-
Configuration of each site may differ according to the track configuration: sites 1 and 2 consisted of ballasted tracks with concrete sleepers and elastic railpads, sites 3–6 were designed by ballasted tracks with azobe sleepers, sites 7 and 8 were defined as elastic track (resting on resilient material), site 9 was a floating slab track and sites 10–14 were represented as a concrete slab track.
-
Sites 10–14 were selected in the same railroad, in order to efficiently compare the effect of building behaviour on structural vibration response.
Figures 6 and 7 present the calculated transfer mobility functions for site 4 (ballasted track) and site 11 (slab track). Coherence curves are also plotted in order to define the frequency range free from measurement errors (typically between 10 and 80 Hz) and the repeatability of each transfer mobility. Dynamic excitation generated within the track is both filtered and dampened by the soil as it propagates. This shows an attenuation with the distance in all the studied frequency range: between track and building foundations, a difference of almost 10 dB is observable. The efficiency of the track type can be evaluated: the track installation has a great influence of the vibratory impact on neighbour buildings. By comparing the two transfer mobilities, it appears that slab tracks generally present a better vibration isolation than classic ballasted tracks. Other findings observed from all the site results revealed that:
-
A mean vibratory level at the track edge was relatively constant and around the value of −60 to 65 dB for ballasted tracks and of −65 to 70 dB for slab tracks;
-
No notable difference between ballasted tracks, including concrete or wood sleepers, were found. A mean attenuation was approximately 15 dB;
-
The only site with floating slab, site 9, caused a very low attenuation. However, only two measurement points were used and, at this stage, it is difficult to draw accurate outcomes. Notice that mean vibratory level at the track edge is close to −75 dB;
-
All the elastic tracks outlined a mean attenuation of around 10 dB. Regarding slab track sites 10–14, the attenuation was relatively close between them (13 dB).
Another interesting finding was that results presented for all sites had a maximum frequency around 20–40 Hz without visible dominant peaks (Tab. 1). This is mainly due to the high soil material damping, masking most often the resonance phenomena.
Lastly, peak particle velocity (PPV) calculated from the impulse response
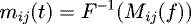 (11)
and defined as the maximum vibration of the signal for each distance
(11)
and defined as the maximum vibration of the signal for each distance
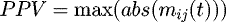 (12)is shown in Figure 8 for all the sites. Overall, a strong decrease with the distance is observed, except for sites 7 and 12 for which the intermediary distance (edge of the sidewalk) presents an elevated level. This is due to the presence of a low wall close to the sensor, playing the role of a wave barrier and amplifying locally the vibration level. As observed in the frequency domain, the site 9 (with floating slab) presents an abnormal level at building foundation. It should be noted that the other sites present a similar decrease rate with the distance, showing the dispersive nature of ground wave. The complex soil configuration (encountered in urban area) plays also an important role in the difference of level between the studied sites. This is one of the reasons why detailed models fail to reproduce very accurate and concise vibration levels in urban area by lacking of soil behaviour information and railway empirical models provide only a good level of magnitude. The use of transfer mobilities incorporates all this information in a single frequency content function. Combined with an accurate description of the force density at the wheel/rail contact (including the local defect behaviour), the resulting vibration can be assessed for any type of vehicle, as defined by equation (5).
(12)is shown in Figure 8 for all the sites. Overall, a strong decrease with the distance is observed, except for sites 7 and 12 for which the intermediary distance (edge of the sidewalk) presents an elevated level. This is due to the presence of a low wall close to the sensor, playing the role of a wave barrier and amplifying locally the vibration level. As observed in the frequency domain, the site 9 (with floating slab) presents an abnormal level at building foundation. It should be noted that the other sites present a similar decrease rate with the distance, showing the dispersive nature of ground wave. The complex soil configuration (encountered in urban area) plays also an important role in the difference of level between the studied sites. This is one of the reasons why detailed models fail to reproduce very accurate and concise vibration levels in urban area by lacking of soil behaviour information and railway empirical models provide only a good level of magnitude. The use of transfer mobilities incorporates all this information in a single frequency content function. Combined with an accurate description of the force density at the wheel/rail contact (including the local defect behaviour), the resulting vibration can be assessed for any type of vehicle, as defined by equation (5).
 |
Fig. 5 Geographical map showing test site locations in Brussels Region. |
 |
Fig. 6 Transfer mobility functions Mij for site 4 (ballasted track): a) magnitude and b) coherence. |
 |
Fig. 7 Transfer mobility functions Mij for site 11 (slab track): a) magnitude and b) coherence. |
Dominant frequencies for all the studied sites.
 |
Fig. 8 Calculated PPV versus distance: the effect of all the studied sites. |
5 Case 2: the typical Athenian concrete building vibration amplification factor in Athens metro network
Compared to other buildings in Europe, the typical Athenian buildings are of differing construction. The structural elements, through which vibration is transmitted, of the load-bearing system of a typical reinforced concrete multi-storey building are slabs, beams, columns, shear walls or central core, and staircases. In general, columns form a square grid of 4–5 m. All of the aforementioned elements, as well as the surrounding walls of any underground floors, and the foundation, are made of cast-in-place concrete. Usually, foundations consist of rigid footings with a height of approximately 1 m and strap beams. The non-structural elements, such as infill and interior walls, are made of hollow clay brick masonry with cement-lime mortar.
In order to estimate the dynamic effect generated by metro networks on buildings, a large experimental campaign was performed on several buildings along the Athens metro lines 2 and 3 (Fig. 9). A complete structural assessment was done at the Public Power Corporation building, close to the metro line 2 under operating conditions, by measuring vibration levels relative to train pass-by and estimating the transmissibility functions (ratio between two transfer mobility functions) at several locations outside and inside the building using impact hammer test. Other buildings were also studied: the Concert Hall, the National Theatre and the Parliament building. Since there were no vibration sources similar to subway trains near these structures, only impact test measurements were performed at the basement or lowest level of each of these structures. Impact on rail was not possible so an alternative way to quantifying vibration was proposed.
Contrary to the aforementioned case, an hammer was used as exciter. Figure 10 shows the location of the impact and the several sensors used to measure the vibration levels. A borehole was drilled 2 m from the facade and a triaxial IEPE accelerometer was mounted on a down hole tool, which was placed in the borehole. Two horizontal and one vertical geophones were mounted on the sidewalk, 2.5 m far from the building. The building interior measurement locations were at the basement, ground floor, 1st floor, 2nd floor, and 4th floor, where vertical geophones were connected to the slabs of the building. The sensitivity of the geophones was 28.8 V/m/s. The measurement setup is described in detail in [36].
Figure 11 shows the transmissibility functions for the different locations inside the building. A special attention was paid to the other sources of vibration by verifying that only vibrations due to impact excitation were recorded. This reveals the building amplification for the three studied floors relative to the basement for basement impacting. For the sake of clarity, spectra curves are presented in one-third octave band. The characteristic building resonances at 16 Hz for all three floors and at 63 Hz for the 1st floor are clearly visible. At the higher frequencies above 63 Hz, the vibration level strongly decrease, showing that the selected frequency range (up to 200 Hz) was sufficient for the present analysis.
In order to characterise the effect of urban light rapid transit passage, the same sensor configuration was used to determine the building vibration levels relative to train pass-by. The Public Power Corporation building amplification factors for the 1st, 2nd, and 4th floors relative to the basement are presented in Figure 12. Except for the 1st floor resonance at 63 Hz, the responses for the three floors are quite similar, as in the case of the impact tests. The frequency content were recorded up to 160 Hz, confirmed by the upper frequency limit from the impact tests. Both results indicate that the resonances are a property of the structure response as opposed to the source.
In addition to the comparison of impact and train passage results, and to confirm that the use of transmissibility results provides interesting findings, it is possible to construct a ‟point-to-line source correction” by subtracting the amplification factor relative to basement impacts from the same amplification factor relative to train pass-by. Thus, by definition, for the Public Power Corporation building, if the correction is added to the building amplification factor relative to basement impacts, the result will yield the building amplification factor relative to train pass-by. It is then possible to apply this correction to impactor data for other building types, where only impactor data exists. A similarity is expected with equation (5)
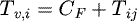 (13)
with Tv,i the transmissibility vibration velocity, Tij the transmissibility function and CF the point-to-line source correction factor, which can be interpreted as a placeholder force factor. The potential sources of error in this approach are:
(13)
with Tv,i the transmissibility vibration velocity, Tij the transmissibility function and CF the point-to-line source correction factor, which can be interpreted as a placeholder force factor. The potential sources of error in this approach are:
-
the difference in distance and orientation of the track relative to the building;
-
the distances from the impactor to the measurement locations;
-
the effect of the construction type on the point to line source correction.
However, at the early stage of vibration assessment, accurate quantitative results are not of primary importance. Figure 13 shows the measured point to line corrections for the three floors obtained by taking the differences of the amplification factors presented above. The correction factor curve shows the approximately 10 dB difference between train and impactor data as well as the difference in attenuation with frequency above 63 Hz. These features are for the most part caused by difference between the sources: the resonances at 16 Hz and at 63 Hz are not present in the correction because they are building properties.
Knowing the different correction factors for each floor, a smoothed average curve can be calculated (see Fig. 13) and used for characterising the impact of metro lines on other buildings. This method was applied to buildings close to line under construction where no metro passage measurement was possible. Some of these buildings were sensitive and a particular attention was paid regarding man-induced vibrations generated during construction and transportation activities [14,37]. Figure 9 shows three sited selected according to their particularities: the Athens Concert Hall (Megaron Mousikis Athinon) is a recent building, inaugurated in 1991 with two halls (four hall actually), presenting for opera performances, and being just outside the metro line 3; the National Theatre was originally founded in 1880 and is a typic neo-classical building, as many other building in Athens; the Parliament building is the first Royal Palace of modern Greece, completed in 1843, and has housed the Hellenic Parliament since 1934. These three buildings give an overall overview of Athenian building types. Figure 14 shows the estimated vibration velocity level calculated from impact tests and the force density provided by the proposed method. Compared to the Public Power Corporation building levels, the levels in these three studied buildings are lower. The levels at Concert Hall are about 10–30 dB lower. The level spread at the National Theatre is less than at the Athens Concert Hall, but greater than that for the Public Power Corporation building. The Parliament building presents intermediate levels, partially due to the differences in construction and size between the Parliament Building and a more standard Hellenic building such as the Public Power Corporation building.
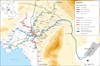 |
Fig. 9 Geographical map showing test site locations in Athens: 1) Public Power Corporation building, 2) the Concert Hall, 3) the National Theatre and 4) the Parliament building. |
 |
Fig. 10 The Public Power Corporation building: location of the experimental setup. |
 |
Fig. 11 Transmissibility functions Tij for Public Power Corporation building. |
 |
Fig. 12 Transmissibility vibration velocity level Tv,i recorded from train pass-by for Public Power Corporation building. |
 |
Fig. 13 Point-to-line source correction LC estimated in the case of Athens metro networks. |
 |
Fig. 14 Transmissibility vibration velocity level Tv,i estimated for train pass-by in other building locations. |
6 Conclusion
Railway–induced ground vibrations can cause negative effects on local communities situated in urban area near the lines. In urban area, these vibrations are a consequence of the vehicle forces acting from the wheels onto the track in local defects. At the early stages of a vibration assessment, it is common to forego rigorous and detailed analysis in preference of a scoping approach. This paper has outlined several experimental analyses in Brussels and in Athens in order to quantify the effect of ground vibrations in a geotechnical context. The main limitation lies on the absence of train excitation in the calculation scheme but such data can be easily combined to a prediction step of train dynamic forces to simulate, for example, the vibration generation in the presence of railway discontinuities [38]. At this stage, it is however proved that the point transfer mobility remains a useful tool to assess the vibration control problems relating to light rapid transit system operations, taking into account local rail defects as potential sources of vibration or the complex path of vibration transmissions.
References
- D.P. Connolly, G. Kouroussis, O. Laghrouche, C. Ho, M.C. Forde, Benchmarking railway vibrations − track, vehicle, ground and building effects, Constr Build. Mater. 92 (2015) 64–81 [Google Scholar]
- G. Kouroussis, C. Conti, O. Verlinden, Building vibrations induced by human activities: a benchmark of existing standards, Mech. Ind. 15 (2014) 345–353 [CrossRef] [Google Scholar]
- D. Stiebel, R. Muller, E. Bongini, A. Ekbald, G. Coquel, A.A. Alguacil, Definition of reference cases typical for hot-spots in europe with existing vibration problems. Technical report, Rivas Project SCP0-GA- 2010 -265754, Report to the EC (deliverable D1. 5), 2012 [Google Scholar]
- UIC High Speed Department, High speed lines in the world. Technical report, International Union of Railways, 2013 [Google Scholar]
- D.P. Connolly, G. Marecki, G. Kouroussis, I. Thalassinakis, P.K. Woodward, The growth of railway ground vibration problems − a review, Sci, Total Environ. 568 (2016) 1276–1282 [Google Scholar]
- C. Madshus, A.M. Kaynia, High-speed railway lines on soft ground: dynamic behaviour at critical train speed, J. Sound Vib. 231 (2000) 689–701 [Google Scholar]
- L. Auersch, S. Said, Attenuation of ground vibrations due to different technical sources, Earthq. Eng. Eng. Vib. 9 (2010) 337–344 [CrossRef] [Google Scholar]
- G. Alexandrou, G. Kouroussis, O. Verlinden, A comprehensive prediction model for vehicle/track/soil dynamic response due to wheel flats, J. Rail Rapid Transit 230 (2016) 1088–1104 [CrossRef] [Google Scholar]
- J. Nielsen, A. Mirza, S. Cervello, P. Huber, R. Müller, B. Nelain, P. Ruest, Reducing train-induced ground-borne vibration by vehicle design and maintenance, Int. J. Rail Transp. 3 (2015) 17–39 [CrossRef] [Google Scholar]
- D. Waddington, J. Woodcock, M.G. Smith, S. Janssen, K.P. Waye, Cargovibes: human response to vibration due to freight rail traffic, Int. J. Rail Transp. 3 (2015) 233–248 [CrossRef] [Google Scholar]
- G. Kouroussis, D.P. Connolly, K. Vogiatzis, O. Verlinden, Modelling the environmental effects of railway vibrations from different types of rolling stock − a numerical study, Shock Vib. 16 (2015) (article ID 142807) [Google Scholar]
- U.S. Department of Transportation (Federal Railroad Administration), High-speed ground transportation. Noise and vibration impact assessment. Technical Report 293630–1, Office of Railroad Development Washington, 1998 [Google Scholar]
- M. Crispino, M. D'Apuzzo, Measurement and prediction of traffic-induced vibrations in a heritage building, J. Sound Vib. 246 (2001) 319–335 [CrossRef] [Google Scholar]
- K. Vogiatzis, Protection of the cultural heritage from underground metro vibration and ground-borne noise in Athens centre: the case of the Kerameikos archaeological museum and Gazi cultural centre, Int. J. Acoust. Vib. 17 (2012) 59–72 [Google Scholar]
- Y. Sato, A. Matsumoto, K. Knothe, Review on rail corrugation studies, Wear 253 (2002) 130–139 [CrossRef] [Google Scholar]
- K. Vogiatzis, G. Kouroussis, Prediction and efficient control of vibration mitigation using floating slabs: practical application at Athens metro lines 2 and 3, Int. J. Rail Transp. 3 (2015) 215–232 [CrossRef] [Google Scholar]
- L. Auersch, Theoretical and experimental excitation force spectra for railway-induced ground vibration: vehicle-track-soil interaction, irregularities and soil measurements, Veh. Syst. Dyn. 48 (2010) 235–261 [CrossRef] [Google Scholar]
- H. Verbraken, H. Eysermans, E. Dechief, S. Francois, G. Degrande, G. Lombaert, Development of a hybrid prediction method for railway induced vibration. In: B. Bergen, P. Sas, (Ed.), ISMA2010 International Conference on Noise and Vibration Engineering, Leuven, Belgium, 2010, pp. 3559–3572 [Google Scholar]
- D.P. Connolly, G. Kouroussis, A. Giannopoulos, O. Verlinden, P.K. Woodward, M.C. Forde, Assessment of railway vibrations using an efficient scoping model, Soil Dyn, Earthq. Eng. 58 (2014) 37–47 [CrossRef] [Google Scholar]
- D.P. Connolly, G. Kouroussis, P.K. Woodward, O. Verlinden, A. Giannopoulos, M.C. Forde, Scoping prediction of re-radiated ground-borne noise and vibration near high speed rail lines with variable soils, Soil Dyn. Earthq. Eng. 66 (2014) 78–88 [Google Scholar]
- G. Kouroussis, D.P. Connolly, G. Alexandrou, K. Vogiatzis, Railway ground vibrations induced by wheel and rail singular defects, Veh. Syst. Dyn. 53 (2015) 1500–1519 [CrossRef] [Google Scholar]
- G. Kouroussis, D.P. Connolly, G. Alexandrou, K. Vogiatzis, The effect of railway local irregularities on ground vibration, Transp. Res. − Part D: Transp. Environ. 39 (2015) 17–30 [Google Scholar]
- G. Kouroussis, O. Verlinden, Prediction of railway induced ground vibration through multibody and finite element modelling, Mech. Sci. 4 (2013) 167–183 [CrossRef] [Google Scholar]
- D. Connolly, A. Giannopoulos, M.C. Forde, Numerical modelling of ground borne vibrations from high speed rail lines on embankments, Soil Dyn. Earthq. Eng. 46 (2013) 13–19 [CrossRef] [Google Scholar]
- G. Kouroussis, D.P. Connolly, O. Verlinden, Railway induced ground vibrations − a review of vehicle effects, Int. J. Rail Transp. 2 (2014) 69–110 [CrossRef] [Google Scholar]
- P. Galvín, J. Domínguez, High-speed train-induced ground motion and interaction with structures, J. Sound Vib. 307 (2007) 755–777 [CrossRef] [Google Scholar]
- P. Alves Costa, R. Calçada, A. Silva Cardoso, A. Bodare, Influence of soil non-linearity on the dynamic response of high–speed railway tracks, Soil Dyn. Earthq. Eng. 30 (2010) 221–235 [Google Scholar]
- D. Connolly, A. Giannopoulos, W. Fan, P.K. Woodward, M.C. Forde, Optimising low acoustic impedance back-fill material wave barrier dimensions to shield structures from ground borne high speed rail vibrations, Constr. Build. Mater. 44 (2013) 557–564 [CrossRef] [Google Scholar]
- O. Laghrouche, D. Le Houédec. Soil–railway interaction for active isolation of traffic vibration. in: B.H.V. Topping, (Ed.), Advances in Simulation and Interaction Techniques, Civil–Comp Ltd, Edinburgh, Scotland, 1994, pp. 31–36 [Google Scholar]
- M. Maldonado, O. Chiello, D. Le Houédec, Propagation of vibrations due to a tramway line, in: Springer/Heidelberg (Ed.), Noise and Vibration Mitigation for Rail Transportation Systems, Proceedings of the 9th International Workshop on Railway Noise, SpringerLink, Berlin, Germany, 2008, vol. 99, pp. 158–164 [Google Scholar]
- G. Kouroussis, N. Pauwels, P. Brux, C. Conti, O. Verlinden, A numerical analysis of the influence of tram characteristics and rail profile on railway traffic ground-borne noise and vibration in the brussels region, Sci. Total Environ. 482–483 (2014) 452–460 [CrossRef] [PubMed] [Google Scholar]
- J.T. Nelson, H.J. Saurenman, A prediction procedure for rail transportation groundborne noise and vibration, Transp. Res. Rec. 1143 (1987) 26–35 [Google Scholar]
- H. Verbraken, G. Lombaert, G. Degrande, Verification of an empirical prediction method for railway induced vibrations by means of numerical simulations, J. Sound Vib. 330 (2011) 1692–1703 [CrossRef] [Google Scholar]
- E.C. Bovey, Development of an impact method to determine the vibration transfer characteristics of railway installations, J. Sound Vib. 87 (1983) 357–370 [CrossRef] [Google Scholar]
- J.-F. Semblat, M.P. Luong, Wave propagation through soils in centrifuge testing, J. Earthq. Eng. 2 (1998) 147–171 [Google Scholar]
- H. Mouzakis, K. Vogiatzis, Ground-borne noise and vibration transmitted from subways networks to a typical Athenian multi-story reinforced concrete building, in: Proceedings of the 23rd International Congress on Sound and Vibration, Athens, Greece, 2016 [Google Scholar]
- H. Mouzakis, Vibrations and cultural heritage in Greece (keynote lecture), in: Proceedings of the 23rd International Congress on Sound and Vibration, Athens, Greece, 2016 [Google Scholar]
- G. Kouroussis, K.E. Vogiatzis, D.P. Connolly, A combined numerical/experimental prediction method for urban railway vibration, Soil Dyn. Earthq. Eng. 97 (2017) 377–386 [CrossRef] [Google Scholar]
Cite this article as: G. Kouroussis, H.P. Mouzakis, K.E. Vogiatzis, Structural impact response for assessing railway vibration induced on buildings, Mechanics & Industry 18, 803 (2017)
All Tables
All Figures
 |
Fig. 1 Setup for vibration propagation tests: a) for distributed source and b) for local source of excitation. |
| In the text | |
 |
Fig. 2 Falling mass machine. |
| In the text | |
 |
Fig. 3 Example of 10 measured impact force samples with the falling mass machine. |
| In the text | |
 |
Fig. 4 Experimental setup and location of the sensors. |
| In the text | |
 |
Fig. 5 Geographical map showing test site locations in Brussels Region. |
| In the text | |
 |
Fig. 6 Transfer mobility functions Mij for site 4 (ballasted track): a) magnitude and b) coherence. |
| In the text | |
 |
Fig. 7 Transfer mobility functions Mij for site 11 (slab track): a) magnitude and b) coherence. |
| In the text | |
 |
Fig. 8 Calculated PPV versus distance: the effect of all the studied sites. |
| In the text | |
 |
Fig. 9 Geographical map showing test site locations in Athens: 1) Public Power Corporation building, 2) the Concert Hall, 3) the National Theatre and 4) the Parliament building. |
| In the text | |
 |
Fig. 10 The Public Power Corporation building: location of the experimental setup. |
| In the text | |
 |
Fig. 11 Transmissibility functions Tij for Public Power Corporation building. |
| In the text | |
 |
Fig. 12 Transmissibility vibration velocity level Tv,i recorded from train pass-by for Public Power Corporation building. |
| In the text | |
 |
Fig. 13 Point-to-line source correction LC estimated in the case of Athens metro networks. |
| In the text | |
 |
Fig. 14 Transmissibility vibration velocity level Tv,i estimated for train pass-by in other building locations. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


