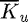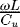| Issue |
Mechanics & Industry
Volume 19, Number 4, 2018
|
|
|---|---|---|
| Article Number | 407 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.1051/meca/2018023 | |
| Published online | 16 November 2018 | |
Regular Article
A hybridised CSAGA method for damage detection in structural elements
1 KIIT University, School of Mechanical Engineering, Kalinga Institute of Industrial Technology,
Bhubaneswar
751024,
Odisha, India
2
National Institute of Technology, Department of Mechanical Engineering,
Rourkela
769008,
Odisha, India
* Corresponding author: e-mail: gudusasmita@gmail.com
Received:
29
August
2017
Accepted:
17
April
2018
In recent years, significant developments have been noticed in nondestructive techniques for damage detection in cracked structures. Some of the proposed methods can be used to find out the existence of the crack; other methods locate and simultaneously find out the damage severity. In the current investigation, a novel hybridised method is proposed for damage detection in structural elements. The proposed method can be used to investigate both location and nature of damage in structures within a reasonable time limit. The problem in the current analysis requires a set of dynamic parameters that depend on the dynamics of the cracked structure due to the presence of the crack. In the present study, the first three natural frequencies of a structure are considered as the inputs to find out the damage location. A finite element method is used to generate the first three natural frequencies of a cracked cantilever beam with multiple cracks. A method hybridizing the nature-inspired artificial intelligence techniques has been implemented for crack detection. Here, clonal selection algorithm and genetic algorithm have been integrated to design the framework of the hybrid technique. The changes in the natural frequencies are given as inputs to the hybrid technique and the output from the technique is the locations of damage.
Key words: damage / vibration / modal parameters / clonal selection / antibody / antigen / genetic algorithm / chromosomes /
© AFM, EDP Sciences 2018
1 Introduction
Damage detection of systems represents an important research topic widely investigated. During the last two decades, several researches have been conducted with reference to beams, trusses, plates, shells, bridges, offshore platforms, and other large civil, aerospace, and composite structures to detect structural damages by monitoring the dynamic response of the systems. The changes in the physical properties cause changes in the modal properties. The aim of this paper is to derive a simple procedure for estimating the damage in structures based on changes in the modal parameters using artificial intelligence (AI) techniques.
Different natural evolution-based AI techniques and vibration analyses [1,2] are used to detect the number, location, and the extent of multiple cracks in structural elements. Free and forced vibration analysis [3] of the cracked structures is also considered for vibration analysis, where the end conditions, materials, geometry [4], and so on are also taken as the decisive parameters. During the mathematical modelling of the crack, most of the authors have considered additional flexibility [5,6] model or reduction in stiffness model. Furthermore, to make the analysis of nonlinearity in the vibration-based fault detection methods, the finite element analysis [7,8] is used. In the recent days, numbers of software packages are available, which makes the analysis easier. Ref. [9] proposed a Hilbert–Huang transform (HHT)-based approach for the detection of damage severity in structural elements. In their investigation, they have validated the effectiveness of HHT method. Ref. [10] proposed an iterative procedure based on regularisation to identify the damages present in buildings. They used a limited noisy vibration measurement as their tool for damage assessment.
The techniques used in the present work are clonal selection algorithm (CSA) and genetic algorithm (GA). CSA is one type of artificial immune system (AIS) [11–13], which describes basic features of natural immune system of our body. AIS-based computational methods [14–16] can be used to find optimal solutions in different applications in several fields. CSA demonstrates the theory that the cells that can recognise the antigens are selected to proliferate. The clonal selection theory (CST) explains the response to an antigenic stimulus in a flexible immune system.
GAs are stochastic search algorithm inspired from the evolutionary principle of natural selection and genetics. The algorithm mainly follows the idea of survival of the fittest first laid down by Charles Darwin. Many real-world problems that are difficult to be solved by traditional methods find an alternative in GAs. From decades, GAs are applied in different fields with good performance efficacy. The GAs are also proposed in many of the works of fault detection [2,17,18]. To improve the efficiency of the GA by significant improvement of convergence performance hybrid, GAs [19,20] have been proposed at different times.
The current work aims at advancing damage detection methods by proposing a hybridisation method for crack detection. The results suggest the evidence of presence of crack. A 2D finite element model was developed to study the modal properties and identify the presence of crack in the structural element. In this paper, the hairline transverse crack is modelled using finite element analysis (FEA). Then, the first three natural frequencies are extracted and converted into relative values from FEA. The relative values of the natural frequencies (rfnf, rsnf, rtnf) are found by comparing the natural frequencies of the uncracked beam and the cracked beam. Relative values of the crack depth and crack location (rcd, rcl) are also found using similar method. This work considers only the natural frequencies because they are less prone to error while calculating. The relative first natural frequency (rfnf), relative second natural frequency (rsnf), and relative third natural frequency (rtnf) are treated as the input variables in the proposed method. The outputs from the system are the relative values of the crack depth (rcd) and crack location (rcl), which in turn contains the information of damage severity. The reason behind the idea to take the relative values of the input and output variables is to lessen the coding error and running time of the algorithm when fed to it. The proposed method is a type of inverse analysis problem. Here, by giving the crack depths and crack locations, the natural frequencies are found out using theoretical, finite element, and experimental analyses. These set of crack locations and first three natural frequencies are used as data set.
2 Theoretical analysis of the cracked beam
In the present work, a cantilever beam with multiple transverse hairline cracks has been modelled. The transverse surface crack is having depth a1 (or a2), width B, and height W. The dimension of the matrix depends on the degrees of freedom. In this work, a 2 × 2 matrix is considered. Here, the cantilever beam is subjected to axial force P1 and bending moment P2, as shown in Figure 1. The application of axial force and bending moment gives coupling with longitudinal and transverse motion.
According to Tada [21], the strain energy release rate at the fractured section can be written as
 (1)
K11 and K12 are the stress intensity factors of mode I (opening of the crack) for load P1 and P2, respectively.
(1)
K11 and K12 are the stress intensity factors of mode I (opening of the crack) for load P1 and P2, respectively.
Taking Ut as the strain energy due to the crack and applying Castigliano's theorem, the additional displacement along the force Pi can be calculated:
 (2)
(2)
By definition, the flexibility influence coefficient Cij, which forms the elements of the flexibility matrix, can be written as
 (3)
(3)
After finding out all the four coefficients of the flexibility matrix, the local stiffness matrix can be obtained by taking the inversion of compliance matrix, that is,
 (4)
(4)
The stiffness matrices for both the cracks are given in the following equations:
 (5)
(5)
 (6)
(6)
From the governing equations of free vibration mode of the cracked beam, the normal function for the system can be defined as follows:
 (7)
(7)
 (8)
(8)
 (9)
(9)
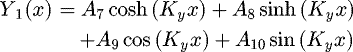 (10)
(10)
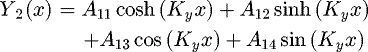 (11)
(11)
 (12)
(12)
Here, U1(x, t), U2(x, t), and U3(x, t) are the normal functions of longitudinal vibration for the sections before and after the crack and Y1(x, t), Y2(x, t), and Y3(x, t) are the normal functions of bending vibration for the same sections.
Analysing the normal functions of the longitudinal and bending vibration conditions, the characteristic equation (the determinant) of the system can be written as follows:
 (13)
(13)
This determinant |Q| is a function of natural circular frequency (ω), the relative location of the crack (β), and the local stiffness matrix (K), which in turn is a function of the relative crack depth (a/W).
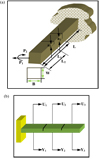 |
Fig. 1 (a) Cracked cantilever beam. (b) Cross-sectional view of cracked cantilever beam. |
3 Finite element analysis of the cracked beam
The ALGOR V 19.3 SP 2 finite element program was used for vibration analysis of the uncracked and cracked cantilever beam. For this purpose, the beam element with different multiple cracks was plotted using CATIA V5R15 software. For this analysis, different crack depths and crack locations were taken. The uncracked and cracked beam model was then analysed in ALGOR environment. First of all, the mesh generation was performed. The mesh size was around 1.4529 mm, and approximately 33 369 elements were created. Then, from the tool command, FEA model was created by using the FEA editor. Thereafter, the parameters such as element type and material name were defined in the ALGOR environment. Then, cantilever boundary conditions were modelled by constraining all degrees of freedom of the nodes located on the left end of the beam. The model unit was then changed to S.I. standards. In the analysis window, the particular analysis type was then selected (natural frequency, i.e. modal analysis). Then, the analysis was performed and the three modes of natural frequencies at different crack locations and crack depths of the cantilever beam were noted down. Figure 2 shows the first three modes of vibration of the cracked beam after finite element analysis.
As already stated in Section 1, the finite element model has been used for the identification of crack. The change in the natural frequencies and modal values during the analysis can be used as crack identification technique.
 |
Fig. 2 Modes of vibration of the cracked beam after finite element analysis. |
4 The clonal selection algorithm
The antigens (Ag) are chosen randomly and are presented to the antibodies in the collection or stock (dataset). The antigens represent the data from the field, that is, the values given from the working area. Here, each antibody and antigen is coded using binary encoding scheme. Then, the antibody population is subjected to affinity measurement. In the present work, Hamming distance method is used for affinity matching operation. The antigens represent the data from the field, that is, the values given from the working area. Antibodies and antigens are presented in Figure 3.
After choosing all the encoding scheme and parameters of the operations, CSA is developed for the described purpose. The main aspects of this kind of immune system are preservation of memory cells functionally disconnected from the repository cloning and selection of the most stimulated cells, rejection of nonstimulated cells, similarity maturation, reselection of the clones with higher affinity, preservation of diversity, and hypermutation proportional to the cell affinity. The following steps describe the algorithm used for the above said purpose.
- i.
A set (Q) of candidate solutions (antibodies) composed of the subset of memory cells (M) added to the remaining (Qr) population (Q = Qr + M) is generated.
- ii.
The antibodies and antigens are encoded (binary encoding) before fitness evaluation. All the individuals in population Q are evaluated using the fitness function for affinity measurement.
- iii.
Based on the affinity measure results, the n best individuals of the population (Qn) are selected.
- iv.
These n best individuals of the population reproduce to form a population of clones (C). The number of clones depends directly on the affinity measurement with the antigen.
- v.
The population of clones is submitted for hypermutation. The mutation rate is indirectly proportional to the affinity of the antibody with the antigen. After mutation, a population (Cm) of mutated clones is generated.
- vi.
The affinity function is again applied to each member of the population (Cm). The highest scoring candidate is credited as the memory cell. If the affinity value for the antigen is greater than the current memory cell, then the new memory cell will replace current memory cell and will become the current memory cell for the next iteration.
- vii.
The antibodies with trivial affinity scores will be replaced by new randomly generated antibodies.
- viii.
Steps (2)–(7) are repeated in each iteration of the algorithm.
The algorithm terminates when it meets the threshold values.
 |
Fig. 3 Presentation of the antibodies and antigens. |
5 The genetic algorithm
GA is inspired from the natural evolution phenomena based on Darwin's theory of natural selection. First, an initial population of candidate solutions are randomly generated which are encoded as chromosomes. The evolution population depends on the principle of survival of the fittest to hopefully produce better and better individuals when the chromosomes (candidate solutions) undergo the genetic operations like selection, recombination, and mutation. In this paper, the chromosomes contain the encoded form of rfnf, rsnf, rtnf, rcd, and rcl. The initial population is generated from the data gathered from FEM and experimental analysis.
The encoding of chromosomes (Fig. 4) used in the current problem is the bit string/binary encoding. Each gene of the chromosome may be either 0 or 1. The gene/bit strings contain the information about the solution.
A fitness function evaluates the fitness of the chromosomes from the set of input variables. A fitness value is computed for each individual in the population. The objective is to find the individual with the highest fitness. After evaluating the fitness of all the initial population candidates, the individuals are ranked according to the fitness. Two of the best candidates are chosen as the parents for crossover operation. For crossover operation, different types of crossovers can be used. Here, two-point crossover (Fig. 5) is used: the parts between these points are crossed and copied between the parents. Figure 5 represents the scheme of two-point crossovers.
After crossover, if needed, mutation (Fig. 6) is operated in the individuals. This operator introduces a change in the chromosome's genes, and new information is added to the population. Mutation also prevents the population from converging too fast and being getting trapped into the local minima. Mutation is always kept short, within the range of 0.001–0.01. Figure 6 represents the mutation operation used in the current work.
The following steps are used in the GA formulation for the current problem.
- 1.
First of all, the variables and fitness function are selected.
GA begins by defining input variables whose values are to be optimised using fitness function and output variables whose values are to be anticipated using genetic operators.
The fitness function to be minimised is defined as follows:
 (14)
(14)
-
fnffld = First natural frequency of the field; fnfx = Relative first natural frequency; snffld = Second natural frequency of the field; snfx = Relative second natural frequency; tnffld =Third natural frequency of the field; tnfx = Relative third natural frequency; i = number of iterations.
-
2.
A data pool (initial population) containing 20 data sets (individuals) is created.
-
3.
This data pool is acquired from FEA and theoretical analysis.
-
4.
Two parents (i.e., two data sets) from data pool (i.e., from 20 data sets) using fitness function are selected.
-
5.
Then, the chosen parents are converted to binary string from decimal values.
-
6.
The binary string is randomly cut at any point for doing crossover.
-
7.
The children (two in numbers) from the parents are found out.
-
8.
Then, the fitness values of the parents and children are compared to find out the best fit member.
-
9.
If the child comes as a best fit, then it is added to the data pool, and a new set of data pool is created.
-
10.
After generating a new population, the process of selection and crossover is repeated.
-
11.
If needed, mutation is done after 20–30 crossovers (if the solution of at least three generations does not vary largely with each other), until we get the best fit for the given set of natural frequencies or the stopping criteria are not met.
-
12.
If a parent comes as the best fit, then the desired output (rcd, rcl) is the output of that set.
-
13.
Steps (2)–(12) are repeated in each iteration, until the algorithm meets the threshold values.
The algorithm terminates when it meets the threshold values.
 |
Fig. 4 Encoded chromosomes. |
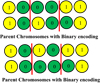 |
Fig. 5 Presentation of two-point crossover process. |
 |
Fig. 6 Presentation of mutation. |
6 Application of the CSAGA method in damage detection
As described in previous sections, in the standard CSA, the population of antibodies evolves rapidly to match the antigens. CSA is devoid of crossover/recombination operation of the antibody gene in the algorithm. But in some cases, crossover can provide a higher level of genetic recombination than mutation. So the recombination operations are borrowed from GA so that there would be introduction of some cross action between the antibodies which will improve the diversity in antibodies after hypermutation.
The fusion can be described in two steps. In the first step, a data pool (initial population) of antibodies evolve rapidly to match the antigens. Both the antigens and antibodies are encoded using binary strings (bits). After the affinity maturation (evaluation of the antibodies according to their fitness values), the selected antibodies undergo proliferation (cloning).
After this point of development of the algorithm, GA is introduced to the sequences of the CSA. Two of the cloned antibodies are selected as the parents for crossover based on the affinity value towards the antigens. Mutation is implemented if the solutions of at least three generations do not vary largely from each other. Rest of the algorithm follows CSA. The stopping criteria for the algorithm are (i) treatment of all the antigens to the antibody population, (ii) number of iterations (100), and (iii) time elapse (3 min). The algorithm terminates if it faces any one of the stopping conditions first. Figure 7 describes the flowchart for the development of hybridisation of CSA and GA.
 |
Fig. 7 Flowchart for CSAGA. |
7 Setup and procedure for experimental analysis
A racked cantilever beam with multiple hairline transverse cracks is rigidly clamped to the concrete foundation base, as shown in Figure 8. Then, the cantilever beam is vibrated manually or by using an impact hammer. The amplitude of vibration of the uncracked and cracked cantilever beam is taken by the accelerometer (vibration pickup) and is fed to the vibration analyser, which is connected to the vibration indicator. The vibration indicator is nothing but a computer system loaded with a PULSE LabShop Software Version 12 for vibration analysis. Then, from the amplitudes of vibration, the natural frequencies for the first three modes of vibration are recorded. The schematic diagram of the experimental setup is given in Figure 9.
In Figures 8 and 9, the numbers are denoted for the following equipment:
- 1.
Cracked cantilever beam with multiple crack
- 2.
Vibration pickup
- 3.
Vibration analyser
- 4.
Vibration indicator
- 5.
Impact hammer
- 6.
Power distribution
The detailed specifications of the accelerometer used in the current study are as follows.
Type: 4513-001
Make: Bruel & Kjaer
Sensitivity: 10–500 mv g−1
Frequency range: 1 Hz to 10 kHz
Supply voltage: 24 V
Operating temperature range: −50 °C to + 100 °C
 |
Fig. 8 Experimental setup. |
 |
Fig. 9 Schematic diagram of experimental setup for free vibration analysis of cracked cantilever beam. |
8 Results and discussions
The results found from the application of the algorithms are given in this section. Here, each individual technique is applied for the detection of damage and they are compared among each other. The formulas used for the calculation of errors are given in equations (15–17).
The percentage of error between FEA result and result from the proposed method is calculated using the following formula:
 (15)
(15)
The percentage of error between experimental result and result from the proposed method is calculated using the following formula:
 (16)
(16)
The total error can be calculated by the following formula:
 (17)
(17)
In this work, modelling of the cracked cantilever beam is done using the change in the local stiffness and flexibility in the vicinity of the crack. Here, Euler–Bernoulli type of beam element is used for simplification. Then, the cracked cantilever beam undergoes finite element analysis to find the first three natural frequencies for different crack locations and crack depths. Thereafter, the relative values of natural frequencies are treated in the proposed methodology to find the damage location.
The proposed algorithm is developed by hybridizing CSA and GA to derive the crack position (location and depth). Running the algorithm within the search space (data set) helps find the near exact, if not exact, location of the crack which helps us to predict the damage severity. The portions of CSA and GA are borrowed from Sections 4 and 5. The algorithm starts by encoding the antibodies antigens using binary encoding scheme. The same numbers of bits are used to encode the input (rfnf, rsnf, rtnf) and output (rcd, rcl) for two cracks, as in Genetic Algorithm section. The combined operators like cloning, crossover, and mutation are described in Figures 5 and 6. The flowchart for the integrated algorithm is shown in Figure 7. The results from the method taken are given in Tables 1–6.
In this work, a hybridised AI technique has been applied to find the crack location in cantilever beam containing multiple cracks. Here, a type of artificial immune system (CSA) has been hybridised with the nature-inspired GA. This is done to introduce exchange of information among the antibodies so that the antibodies are improved and the convergence speed is reduced. Here, 6 bits are taken for binary encoding of the antibodies and antigens, the initial population size is set at 30, and the maximum iterations (generations) for the algorithm is set at 100, which is one of the termination conditions of the algorithm. The formulas for the calculations of different errors are provided in equations (15–17).
9 Conclusions
The conclusions from the proposed work are given in the following steps.
Being an inverse engineering problem, when the first three natural frequencies are fed to the proposed algorithm (which is developed by hybridising CSA and GA), it provides the crack location. Then, by running the algorithm within the search space (data set), it helps us to find the near exact, if not exact, location of the crack which in turn helps us to predict the damage severity. This work can be used to predict the rest of the life of the structural element because the results directly give the crack depth and crack location. The rest of the discussion provides robustness and efficiency of the hybridised algorithm.
Tables 1–3 provide the comparison of the results of the FEA with the results of CSAGA, CSA and GA, respectively. Similarly, Tables 4–6 provide the comparison of the results of the experimental analysis with CSAGA, CSA, and GA, respectively.
The errors for CSA are found to be 3.3155% and 3.7835% in comparing the results with the results of the FEA and experimental analysis, respectively. While applying GA to the current problem, the errors are found to be 3.7295% and 4.343% in comparing the results with the results of the FEA and experimental analysis, respectively. Similarly, when the CSAGA technique is applied, the errors show a remarkable fall to 2.328% and 3.308% in comparing the results with the results of the FEA and experimental analysis, respectively.
From the above analysis of the results, it can be concluded that the CSAGA produces better results compared to the stand-alone algorithms. The improvements in the results are the effects of the hybridisation process. Due to the integration of GA in standard CSA, the information exchange between the antibodies is enhanced which improves the global search capability of the algorithm. This is a novel hybridisation methodology that can be applied to damage detection in structural elements along with prediction of damage severity. By preprocessing of vibration signatures of the system to the proposed methodology, early prediction of possible damages can be made and it can stop catastrophic failures of structures.
Comparison of the results from CSAGA and FEA.
Comparison of the results from CSA and FEA.
Comparison of the results from GA and FEA.
Comparison of the results from CSAGA and experimental analysis.
Comparison of the results from CSA and experimental analysis.
Comparison of the results from GA and experimental analysis.
Nomenclature
A: Cross-sectional area of the beam
Aii = 1–12: Unknown coefficients of matrix A
E: Young's modulus of elasticity of the beam material
Fii = 1,2: Experimentally determined function
K1,ii = 1,2: Stress intensity factors for Pi loads
L1: Location (length) of the crack from fixed end
Mii = 1,4: Compliance constant
Pii = 1,2: Axial force (I = 1), bending moment (i = 2)
Q: Stiffness matrix for free vibration
rcd: Crack depth in dimensionless form (relative)
rcl: Crack location in dimensionless form (relative)
fnf: First natural frequency in dimensionless form (relative)
Sij: Local flexibility matrix elements
snf: Second natural frequency in dimensionless form (relative)
tnf: Third natural frequency in dimensionless form (relative)
Uii = 1,2: Normal functions (longitudinal)
Y0: Amplitude of the exciting vibration
Yii = 1,2: Normal functions (transverse)
References
- N.T. Khiem, H.T. Tran, A procedure for multiple crack identification in beam-like structures from natural vibration mode, J. Vib. Control 20 (2014) 1417–1427 [CrossRef] [Google Scholar]
- S. Zheng, X. Liang, H. Wang, D. Fan, Detecting multiple cracks in beams using hierarchical genetic algorithms, J. Vibroeng. 16 (2014) 1153 [Google Scholar]
- A.R. Daneshmehr, A. Nateghi, D.J. Inman, Free vibration analysis of cracked composite beams subjected to coupled bending-torsion loads based on a first order shear deformation theory, Appl. Math. Model. 37 (2013) 10074–10091 [CrossRef] [Google Scholar]
- R.S. Pawar, S.H. Sawant, An overview of vibration analysis of cracked cantilever beam with non-linear parameters and harmonic excitations, Int. J. Innov. Technol. Exploring Eng. 8 (2014) 53–55 [Google Scholar]
- M.A. Musmar, M.I. Rjoub, M.A. Hadi, Nonlinear finite element analysis of shallow reinforced concrete beams using SOLID65 element, Elastic, 25743 (2006) 0–3 [Google Scholar]
- P. Parandaman, M. Jayaraman, Finite element analysis of reinforced concrete beam retrofitted with different fiber composites, Middle East J. Sci. Res. 22 (2014) 948–953 [Google Scholar]
- J.K. Sinha, M.I. Friswell, S. Edwards, Simplified models for the location of cracks in beam structures using measured vibration data, J. Sound Vib. 251 (2002) 13–38 [CrossRef] [Google Scholar]
- S. Caddemi, A. Morassi, Multi-cracked Euler-Bernoulli beams: mathematical modeling and exact solutions, Int. J. Solids Struct. 50 (2013) 944–956 [CrossRef] [Google Scholar]
- W.L. Chiang, D.J. Chiou, C.W. Chen, J.P. Tang, W.K. Hsu, T.Y. Liu, Detecting the sensitivity of structural damage based on the Hilbert-Huang transform approach, Eng. Comput. 27 (2010) 799–818 [CrossRef] [Google Scholar]
- H.P. Chen, N. Bicanic, Identification of structural damage in buildings using iterative procedure and regularisation method, Eng. Comput. 27 (2010) 930–950 [CrossRef] [Google Scholar]
- S. Parsazad, E. Saboori, A. Allahyar, Data selection for semi-supervised learning. arXiv preprint, arXiv:1208.1315 (2012) [Google Scholar]
- B. Chen, C. Zang, Artificial immune pattern recognition for structure damage classification, Comput. Struct. 87 (2009) 1394–1407 [CrossRef] [Google Scholar]
- J. Strackeljan, K. Leiviskä, Artificial immune system approach for the fault detection in rotating machinery, Proc. CM (2008) 1365–1375 [Google Scholar]
- S. Tamandani, M. Hosseina, M., Rostami, A. Khanjanzadeh, Using clonal selection algorithm to optimal placement with varying number of distributed generation units and multi objective function, World J. Control Sci. Eng. 2 (2014) 12–17 [Google Scholar]
- M. Vairamuthu, S. Porselvi, A.N. Balaji, J. Rajesh Babu, Artificial immune system algorithm for multi objective flow shop scheduling problem, Int. J. Innov. Res. Sci. Eng. Technol. 3 (2014) 1391–1395 [Google Scholar]
- H. Yang, T. Li, X. Hu, F. Wang, Y. Zou, A survey of artificial immune system based intrusion detection, Sci. World J. (2014) 1–11 [Google Scholar]
- N. Khaji, M. Mehrjoo, Crack detection in a beam with an arbitrary number of transverse cracks using genetic algorithms, J. Mech. Sci. Technol. 28 (2014) 823 [CrossRef] [Google Scholar]
- M.T. Vakil-Baghmisheh, M. Peimani, M.H. Sadeghi, M.M. Ettefagh, Crack detection in beam-like structures using genetic algorithms, Appl. Soft Comput. 8 (2008) 1150–1160 [CrossRef] [Google Scholar]
- Y.G. Xu, G.R. Li, Z.P. Wu, A novel hybrid genetic algorithm using local optimizer based on heuristic pattern move, Appl. Artif. Intell. 15 (2001) 601–631 [CrossRef] [Google Scholar]
- H. Guan, Y. Chen, P. Du, Study of an improved clonal selection algorithm and its application, Int. J. Digit. Content Technol. Appl. 6 (2012) 323 [Google Scholar]
- H. Tada, P.C. Paris, G.R. Irwin, The stress analysis of cracks, Handbook, Del Research Corporation, 1973 [Google Scholar]
Cite this article as: S. Sahu, P.B. Kumar, D.R. Parhi, A hybridised CSAGA method for damage detection in structural elements, Mechanics & Industry 19, 407 (2018)
All Tables
All Figures
 |
Fig. 1 (a) Cracked cantilever beam. (b) Cross-sectional view of cracked cantilever beam. |
| In the text | |
 |
Fig. 2 Modes of vibration of the cracked beam after finite element analysis. |
| In the text | |
 |
Fig. 3 Presentation of the antibodies and antigens. |
| In the text | |
 |
Fig. 4 Encoded chromosomes. |
| In the text | |
 |
Fig. 5 Presentation of two-point crossover process. |
| In the text | |
 |
Fig. 6 Presentation of mutation. |
| In the text | |
 |
Fig. 7 Flowchart for CSAGA. |
| In the text | |
 |
Fig. 8 Experimental setup. |
| In the text | |
 |
Fig. 9 Schematic diagram of experimental setup for free vibration analysis of cracked cantilever beam. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.