| Issue |
Mechanics & Industry
Volume 20, Number 2, 2019
|
|
|---|---|---|
| Article Number | 203 | |
| Number of page(s) | 6 | |
| DOI | https://doi.org/10.1051/meca/2019005 | |
| Published online | 19 April 2019 | |
Regular Article
Thermo-mechanical behavior of a granular media in a rotating drum
1
Département de Génie Mécanique, Université 20 Août 1955 de Skikda, BP 26, Skikda 21000, Algeria
2
Université de Montpellier, CNRS, LMGC, UMR5508, 34095 Montpellier, France
3
Université de Lyon, CNRS INSA-Lyon, LaMCoS, UMR 5259, 69621 Villeurbanne Cedex, France
* e-mail: teyar.soumia@yahoo.fr
Received:
26
June
2018
Accepted:
24
January
2019
In the complex granular flow, the shear and flow of particles lead to increase in temperature that can enchain behavioral modifications. However, their thermo-mechanical and electrical behavior is of great interest for applications such as rail transport, grinding, and granular material reproduction systems. To study these behaviors, a numerical experiment is carried out on a rotating drum model. This device makes it possible to generate continuous and controlled free surface flows. Relying on the NSCD approach, the location of the hottest zone and the evolution of the temperature are correlated with the evolution of the velocity field.
Key words: Granular media / rotating drum / discrete element method / heat transfers / friction
© AFM, EDP Sciences 2019
1 Introduction
According to external solicitations, a granular medium can resist to compression like a solid [1] or flows like a fluid [2]. In several situations, these two behaviors cohabit and lead to nontrivial analysis of the resulting behavior. It is typically the case in natural systems like rock avalanches [3] but also in several sectors of industry (mining [4], food processing [5], and civil engineering [6]). In the literature, the most common apparatus used to analyze such systems appears as the rotating drum. According to a given rotation speed, it is possible to generate different flow regimes (avalanche [7], curved and S [8]). Moreover, for a specific range of rotation speeds, the generated free surface flow is flat according to a given angle [9]. Recent works [10,11] have shown the influence of the operating conditions of the drum (diameter of the drum, drum width, rotation speed, report of particle size, and particle roughness) on the flow properties. However, the most part of the literature analyses the mechanical response of the system but any consideration is done on its thermal properties, from a local point of view at least. Especially, the location of the heat elevation is unknown as well as the increase of temperature according to external solicitations or local properties. In the present paper, an analysis of granular flows is proposed from a mechanical–thermal point of view. Thus, after a presentation of the numerical framework in the Section 3, concerning the mechanical and thermal equations needed for the numerical study, the Section 3 will present results and discussion concerning the numerical simulation campaign.
2 Numerical framework
Several approaches allow the modeling of granular flow in the literature. Basically, there are two kinds of approaches: smooth discrete element model [12] and non-smooth discrete element model [13]. The first class of models determines contact forces using local spring-dashpot model [14], while the second one considers a unilateral description of contact conditions [13]. The present model belongs to the second class, which is well suited for long time simulations, as large time step can be used. Thus, the numerical frame work relies on the non-smooth contact dynamics approach (NSCD) proposed by Jean [13] and Moreau [15] and extends to thermal coupling with the strategy proposed by Renouf et al. [16].
2.1 Mechanical part
The mechanical formulation is initiated by the general equation of dynamics for the granular system: (1)where
(1)where  is the mass matrix
is the mass matrix 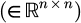 ,
, 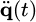 the acceleration vector or the second derivative of the configuration vector
the acceleration vector or the second derivative of the configuration vector 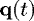 , F
ext the applied external forces on the particles in contact, and
, F
ext the applied external forces on the particles in contact, and 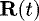 the contact force vectors related to local rubbing contacts.
the contact force vectors related to local rubbing contacts.
The system (1) written in terms of global variable (attached to particle within the system) is rewritten in term of local variables as they appear to be the main unknowns of the multi-contact problem (more details can be found in Jean's initial works [13]).
Thus, considering the local couple impulse/relative velocity  , the system is rewritten as follows:
, the system is rewritten as follows: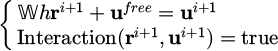 (2)where
(2)where  is called Delassus matrix [15].
is called Delassus matrix [15].
The system (2) is then solved using a nonlinear Gauss–Seidel type (NLGS) [13]. It makes it possible to calculate at the same time the relative velocities (u i ) between particles in contact and the contact forces (r i+1) taking into account the laws of interaction between particles. The convergence is robust and a parallel version ensures the decrease of CPU time [17].
The interaction law used to manage contact forces derives from the Signorini–Coulomb condition [13]. It considers a non-penetration between the particles and the normal component of the local impulse remains positive (no regularization), summarized by the well known complementary problem: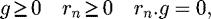 (3)where g represents the gap between particles. To be able to manage restitution between particles, the equation (3) is written in term of velocity and combined to the Newton restitution law [18], which connects the velocity before and after impact as:
(3)where g represents the gap between particles. To be able to manage restitution between particles, the equation (3) is written in term of velocity and combined to the Newton restitution law [18], which connects the velocity before and after impact as: (4)where e
n
is the normal restitution coefficient. The tangential part is governed by a Coulomb friction law which ensures that the tangential component of the local force, denoted r
t
, remains in the normal cone:
(4)where e
n
is the normal restitution coefficient. The tangential part is governed by a Coulomb friction law which ensures that the tangential component of the local force, denoted r
t
, remains in the normal cone: (5)where μ is the Coulomb friction coefficient.
(5)where μ is the Coulomb friction coefficient.
2.2 Thermal part
The formulation used for the thermal model allows to simulate the phenomena of friction heat generation and conduction heat transfer. As the temperatures considered are low, heat transfer by radiation and convection is neglected. The thermal evolution of a single particle is then related to the following equation: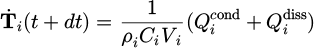 (6)where ρ
i
C
i
V
i
represents the thermal capacity of the considered particle and dt the discretization time step. The local heat generation is related to the local mechanical energy dissipation and is computed as:
(6)where ρ
i
C
i
V
i
represents the thermal capacity of the considered particle and dt the discretization time step. The local heat generation is related to the local mechanical energy dissipation and is computed as: (7)where
(7)where 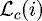 is the list of contact involving the particle i. It is recalled that r and u are respectively the contact forces and relative velocities to the contact. The transfer of the local heat by conduction between the particles i and its neighbor j is written by:
is the list of contact involving the particle i. It is recalled that r and u are respectively the contact forces and relative velocities to the contact. The transfer of the local heat by conduction between the particles i and its neighbor j is written by: (8)where (T
i
−T
j
) is the difference of temperature between the particles i and j, while H
α
is the thermal conductance. Based on the Hertz theory, it is possible to have a relation between the contact force and the contact area. In a two-dimensional model H
α
is expressed as follow:
(8)where (T
i
−T
j
) is the difference of temperature between the particles i and j, while H
α
is the thermal conductance. Based on the Hertz theory, it is possible to have a relation between the contact force and the contact area. In a two-dimensional model H
α
is expressed as follow: (9)where r* and E
* are respectively the effective radius and Young modulus while k
th represents the thermal conductivity [19].
(9)where r* and E
* are respectively the effective radius and Young modulus while k
th represents the thermal conductivity [19].
2.3 Numerical model
As proposed in the introduction, a two-dimensional rotating drum (Fig. 1) is used to simulate particle flows. The drum radius, denoted R 0, is equal to 0.3 m. It is half filled with rigid circular particles with a radius uniformly distributed between 2 and 3 mm. To avoid boundary sliding and to be sure that particles are driven into the rotation of the drum to generate a global flow, the friction coefficient between the particles and the drum is equal to 0.9 to mimic experimental conditions (drum roughness or dents) [2]. The simulation time step is equal to 10−3s, ensuring a good compromised between CPU time and solution accuracy.
Then, two parameters have been modified: the rotation speed, Ω, to check the influence of external solicitations; and the friction between particles, μ, to check the impact of internal properties. A first set of simulations has been realized for values of Ω equal to 4, 6, 8, 10, and 16 rpm with a value of μ equal to 0.3. Then a second set uses values of μ ranging from 0.3 to 0.9 with a rotation speed equal to 16 rpm. Simulation data are summarized in Table 1.
Each simulation is run until reaching a stabilized regime corresponding to a constant continuous surface flow. In this phase, quantities as the surface flow angle and the velocity profile across the thickness are measured. Such measures are completed with the measure of thermal quantities as the temperature gradient ΔT across the thickness. Simulations run on the LMGC90 open-source plate-forme1.
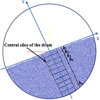 |
Fig. 1 Numerical visualization of the rotating drum. |
Numerical parameters.
3 Results
3.1 Velocity profiles
First, different mechanical quantities are measured according to the evolution of rotating speed and local friction. The different steady state flows are illustrated on the Figure 2 with the visualization of the velocity magnitude for the rotating velocity equal to 4 (a), 6 (b), 10 (c), and 16 (d) rpm.
In each case, the maximal value of the velocity is located in the flowing zone, close to the free surface. Such a zone is characterized by its thickness called rolling thickness which is constant in a steady state regime. The free surface is flat for the rotating speed of 4, 6, 8, and 10 rpm. For the higher value (i.e. 16 rpm on Fig. 2d), a well known S-shape surface is observed.
In each case, one could observe the existence of two distinguished phases in the granular media: a “static phase” which moves with the drum and a “dynamic phase” located at the free surface which exhibit, as said before, the maximal value of velocity.
The inclination angle of this surface, denoted θ, and the rolling thickness of the dynamic phase, denoted H, are both function of Ω (cf. Fig. 3).
The inclination angle appears as an almost linear function of Ω. Such a result has been obtained in previous results of the literature [2,10]. The gradient of this function depends on the system properties and especially on the ratio D/d (diameter of the drum/diameter of particles). The evolution of H could also be assimilated to a linear function with the same dependencies of system properties.
Figure 4 presents the evolution of the velocity at the center of the drum as a function of the normalized sample thickness H/d for different rotation speeds. The evolution of such profiles underlines the existence of the two different phases: a static one for which the velocity is close to 0 and a dynamical one where the velocity increases linearly with the thickness. Such a behavior has already been presented in previous studies as for example in [2] or [10]. Moreover, it is important to notice that the velocity gradient within the flowing surface is independent of Ω, for the considered flow regimes. The evolution of H mentioned previously could also be observed in such a curve. Indeed the value of H corresponds to the range where V/ΩR 0 is linear. Figure 4 presents the evolution of such profiles for the different rotation speeds and Figure 5 for the different local friction coefficients.
In complement of Figure 4, the velocity profiles are plotted as a function of the local friction (cf. Fig. 5).
It is interesting to note that the friction has no influence on such profiles. Indeed, in the static phase where the number of contact is fixed, the friction affects only the compacity. In the flowing phase, contacts are binaries, the density is lower than in the static phase and the contribution of friction is not important.
 |
Fig. 2 Visualization of the particle velocity field for the rotating velocity equals to 4 (a), 6 (b), 10 (c), and 16 (d) rpm. |
 |
Fig. 3 Evolution of the inclination angle θ (a) and the rolling thickness H (b) as a function of the drum rotating speed Ω. |
 |
Fig. 4 Velocity profiles in the central slice of the drum for the different rotational velocities of the drum V x = f (Y). |
 |
Fig. 5 Velocities profiles in the central slice of the drum for different friction coefficients. |
3.2 Temperature profiles
Finally, in complement of velocity profiles, the evolution of temperature is analyzed within the drum. The same kind of profiles is computed to exhibit the evolution of the temperature across the sample thickness. Figure 6 presents a typical snapshot of the temperature field within the system.
Figures 7 and 8 present respectively the evolution of the temperature across the sample thickness at the center of the drum for different rotating speeds and different friction coefficients.
The change in temperature is relatively weak due to the shear, which is itself low (ΔT = 0.02 K). The maximal value of temperature (T max) is located deeper in the thickness of the drum according to the rotating speed: higher is Ω, deeper is T max. This is directly related to the increase of the thickness of the flowing zone. When the friction increases the elevation of temperature is not so important according to the increase of local friction.
Both results can be explained by the fact that the place where the macroscopic shear is located is at the interface between the two phases. Indeed, the heat generated in the two zones is lower than the friction between the two phases. The dissipation due to local friction is not activated in the static zone neither in the flowing one: in the static zone, there is no relative motion between particles and in the flowing one, the particles go mostly in the same direction, causing some dissipation due to impacts. On the contrary, at the interface between the two zones, the “macroscopic friction”, which represents the shearing of the flowing zone on the static one, is important and independent of local properties as the velocity gradient is constant. Thus, the generated heat is diffused between contacting particles by conduction, starting from the generation area (the shear and the friction are max) until the free surface of flow and the wall of the drum, where are localized the minimum values of temperature.
To complete such observation, the Figure 9 presents the position of the hottest particle is plotted as a function of rotational speed. The figure shows that drums rotational velocity Ω has a significant influence on the evolution of the particle temperature.
For the different simulations, it appears that the hottest particle gradually moves toward the center of the drum with variations depending of the rotating speed. Such a motion creates a natural convection within the medium favoring the diffusion of heat within the system.
 |
Fig. 6 Visualization of the particle temperature field for the rotating velocity equal to 4 (a), 6 (b), 10 (c), and 16 (d) rpm. |
 |
Fig. 7 Maximal value of temperature in the drum central slice for different rotation speeds. |
 |
Fig. 8 Maximal value of temperature in the drum central slice for different friction coefficients. |
 |
Fig. 9 Position of the hottest particle as a function of rotational speed. The opacity of the point is related to its measuring time: the darker is the point, the larger is its position in the simulation time. |
4 Conclusion
This work presents the influence of the rotational speed of the drum and the local coefficient of friction on the thermo-mechanical behavior of the medium. The increase of the drum rotational velocity produces an angle of inclination of the free surface most important which leads to a shorter flow of the free surface. Moreover, the drum rotational velocity induces a shear between the two different phases of the system and generates a significant amount of heat. The local coefficient of friction between particles has a non-significant influence on the velocity of the flowing surface and on the temperature within the medium.
A heat flow analysis within the medium can also be proposed (cf. Fig. 10):
Qrec represents the recycled heat flux which produces by the flow of the particles to the free surface and near the wall of the drum.
Qdiss represents the internal source flow or heat flux generated by friction of the particles in the transition zone with the circular motion of the particles of the static zone and the continuous flow of the particles of the dynamic zone.
Qcond represents the heat flux by conduction between the particles. It disperses non-uniform in the medium because of different particle flows in both zones.
Such model could be applied to the analysis of thermo-mechanical behavior of granular flows in view to locate the preferential area of heat generation, which could affect the mechanical properties as well.
 |
Fig. 10 Heat transfer in the rotating drum. |
References
- F. Radjai, M. Jean, J.J. Moreau, S. Roux, Force distributions in dense two dimensional granular systems, Phys. Rev. Lett. 77 (1996) 264–277 [Google Scholar]
- D. Bonamy, F. Daviaud, L. Laurent, Experimental study of granular surface flows via a fast camera: a continuous description, Phys. Fluids 14 (2002) 1666–1673 [CrossRef] [Google Scholar]
- P.A. Cundall, A computer model for simulating progressive large scale movements in Blocky Rock Systems, Proc. Symp Int. Soc. Rock Mech. 1 (1971) 132–150 [Google Scholar]
- J.J. Zhao, J.G. Xiao, M.L. Lee, Y.T. Ma, Discrete element modeling of a mining-induced rock slide. SpringerPlus 5 (2016) 1633 [CrossRef] [PubMed] [Google Scholar]
- J.D. Oroná, S.E. Zorrilla, J.M. Peralta, Computational fluid dynamics combined with discrete element method and discrete phase model for studying a food hydrofluidization system, Food Bioprod. Process. 102 (2017) 278–288 [CrossRef] [Google Scholar]
- G. Saussine, C. Cholet, F. Dubois, C. Bohatier, P.E. Gautier, J.J. Moreau, Modelling ballast behaviour under dynamic loading. Part 1: a 2D polygonal discrete element method approach, Comput. Methods Appl. Mech. Eng. 195 (2006) 2841–2859 [CrossRef] [Google Scholar]
- J. Rajchenbach, Flow in powders: from discrete avalanches to continuous regime, Phys. Rev. Lett. 65 (1990) 2221 [CrossRef] [PubMed] [Google Scholar]
- N. Taberlet, P. Richard, E.J. Hinch, S shape of a granular pile in a rotating drum, Phys. Rev. E 73 (2006) 050301 [CrossRef] [Google Scholar]
- G. Felix, V. Falk, U. D'Ortona, Granular flows in a rotating drum: the scaling law between velocity and thickness of the flow, Eur. Phys. J. E 22 (2007) 25–31 [CrossRef] [EDP Sciences] [Google Scholar]
- M. Renouf, D. Bonamy, F. Dubois, P. Alart, Numerical simulation of 2D steady granular flows in rotating drum: on surface flows rheology, Phys. Fluids 13 (2005) 103303 [CrossRef] [Google Scholar]
- N.A. Pohlman, B.L. Severson, J.M. Ottino, R.M. Lueptow, Surface roughness effects in granular matter: influence on angle of repose and the absence of segregation, Phys. Rev. E 73 (2006) 031304 [CrossRef] [Google Scholar]
- P.A. Cundall, O.D.L. Strack, A discrete numerical model for granular assemblies, Géotechnique 29 (1979) 47–65 [CrossRef] [Google Scholar]
- M. Jean, The non-smooth contact dynamics method, Comp. Methods Appl. Math. Eng. 177 (1999) 235–257 [Google Scholar]
- J. Shunying, H.S. Hayley, Effect of contact force models on granular flow dynamics, J. Eng. Mech. 11 (2006) 1252–1259 [Google Scholar]
- J.J. Moreau, Unilateral contact and dry friction in finite freedom dynamics, in: J.J. Moreau, P.D. Panagiotopoulos (Eds.), Nonsmooth Mechanics and Applications, Springer, Vienna, 1988, pp. 1–82 [Google Scholar]
- M. Renouf, H.P. Cao, V.H. Nhu, Multiphysical modeling of third-body rheology, Tribol. Int. 44 (2011) 417–425 [CrossRef] [Google Scholar]
- M. Renouf, F. Dubois, P. Alart, A parallel version of the Non Smooth Contact Dynamics Algorithm applied to the simulation of granular media, J. Comput. Appl. Math. 168 (2004) 375–382 [CrossRef] [MathSciNet] [Google Scholar]
- M. Mabrouk, Liaisons unilatérales et chocs élastiques quelconques: un résultat d'existence, C. R. Acad. Sci. I Math. 326 (1998) 1353–1357 [Google Scholar]
- M.M. Yovanovitch, Thermal contact resistance across elastically deformed spheres, J. Spacecr. Rockets 4 (1967) 119–122 [CrossRef] [Google Scholar]
Cite this article as: S. Teyar, M. Renouf, Y. Berthier, Thermo-mechanical behavior of a granular media in a rotating drum, Mechanics & Industry 20, 203 (2019)
All Tables
All Figures
 |
Fig. 1 Numerical visualization of the rotating drum. |
| In the text | |
 |
Fig. 2 Visualization of the particle velocity field for the rotating velocity equals to 4 (a), 6 (b), 10 (c), and 16 (d) rpm. |
| In the text | |
 |
Fig. 3 Evolution of the inclination angle θ (a) and the rolling thickness H (b) as a function of the drum rotating speed Ω. |
| In the text | |
 |
Fig. 4 Velocity profiles in the central slice of the drum for the different rotational velocities of the drum V x = f (Y). |
| In the text | |
 |
Fig. 5 Velocities profiles in the central slice of the drum for different friction coefficients. |
| In the text | |
 |
Fig. 6 Visualization of the particle temperature field for the rotating velocity equal to 4 (a), 6 (b), 10 (c), and 16 (d) rpm. |
| In the text | |
 |
Fig. 7 Maximal value of temperature in the drum central slice for different rotation speeds. |
| In the text | |
 |
Fig. 8 Maximal value of temperature in the drum central slice for different friction coefficients. |
| In the text | |
 |
Fig. 9 Position of the hottest particle as a function of rotational speed. The opacity of the point is related to its measuring time: the darker is the point, the larger is its position in the simulation time. |
| In the text | |
 |
Fig. 10 Heat transfer in the rotating drum. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


