| Issue |
Mechanics & Industry
Volume 21, Number 6, 2020
|
|
|---|---|---|
| Article Number | 602 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.1051/meca/2020074 | |
| Published online | 25 September 2020 | |
Regular Article
An investigation on dynamic characteristics of herringbone planetary gear system with torsional flexibility between the left and right teeth of the sun gear
School of Mechanotronics and Vehicle Engineering, Chongqing Jiaotong University, ChongQing 400074, China
* e-mail: xxiangyang@hotmail.com
Received:
24
April
2020
Accepted:
30
August
2020
Herringbone planetary gear system (HPGS) has high power density and complex structure. The torsional flexibility of the left and right teeth of the sun gear is closely related to the dynamic characteristics of the HPGS. In this research, considering the coordination conditions of both sides torsional stiffness and axial slide of the sun gear, a new dynamic model of the HPGS considering the meshing phase difference between left and right teeth of the sun gear is developed based on the lumped-parameter method, and the influence mechanism of torsional stiffness and axial sliding is studied. Moreover, the dynamic parameters and dynamic characteristics of the HPGS are analyzed in the case of varying torsoinal stiffness and axial slide. The results show that the torsional stiffness of left and right teeth and the axial slide of sun gear have significant impacts on the dynamic parameters and dynamic mesh force response. With the increase of the torsional flexibility (the decrease the torsional stiffness), the sun gear and planet gear meshing stiffness and the maximum tooth surface load are both increased on the left side (input side) and decreased on the right side, but the main peak values and peak frequencies of dynamic response on both sides of the s-p meshing pairs decrease significantly. In addition, when the sun gear slides toward the output side axially, meshing stiffness and dynamic mesh force response main peak values decreased on the left side (input side) and increased on the right side, but the main resonance peaks frequencies keep the same.
Key words: Herringbone planetary gear / sun gear / torsional flexibility / meshing stiffness / dynamic characteristics
© AFM, EDP Sciences 2020
1 Introduction
With the increasing power of wind turbines, the aero-space equipment, large machine tools, etc., the herring-bone planetary gear system (HPGS) has become the main research fields of planetary gear transmission system for its distinctive advantages of more compact structure, higher power density and greater carrying capacity. The traditional dynamic characteristics design for general planetary gear transmission system is difficult to meet this type high power application requirements more and more. Thus, increasing the flexibility of this kind of system is an momentous research direction to obtain better load distribution and dynamic characteristics. Therefore, in the research of HPGS, it has great practical significance to study gears dynamic load when torsional flexibility of the two symmetrical sides of the herringbone sun gear is considered.
Currently, some scholars have conducted a series of researches on the dynamic characteristics of the HPGS. Lin, J., and Parker, R. G [1] proposed a planar dynamic model of planetary gears and summarized three vibration modes of plane vibration. Zhang and Zhu [2] developed a novel dynamic model of HPGS considering the meshing phase, and analyzed the influence of meshing phase on load sharing. Sondkar et al. [3] proposed a dynamic model of the HPGS, which includes the degrees of freedom of torsion, translation and rotation of rotating components, and found that the stagger on both sides has a significant effect on the dynamic response of HPGS. Bu et al. [4] studied the modal characteristics by establishing a generalized linear model of the HPGS with three plane degrees of freedom, simultaneously deriving a different relationship between planet deflections under the translation mode. Zhu [5] and Xu et al. [6] analyzed the dynamic characteristics and the load sharing performance by establishing a planetary gear dynamic model with flexible pins. Wang et al. [7] considered the effects of friction and multiple backlashes while taking axial vibration into consideration, then established a dynamic model of the herringbone gear set, and solved the dynamic equation with an example. Wang et al. [8] optimized the vibration of the herringbone gear and proposed a sixth-order polynomial transmission error function for reducing vibration and shock. Mo et al. [9,10] proposed a dynamic model of the HPGS, found that the torsional stiffness has a certain impact on the natural characteristics and load sharing. Liu [11] and Ren et al. [12] proposed a generalized model of the HPGS, which can be used to analyze the variable process and the effect of manufacturing errors on the dynamic floating performance of the system. Chen and Shao [13] considering gear tooth errors, and developed a dynamic model of planet gear, which is used to analyze the meshing stiffness of mesh pairs, and employed in any situation to analyze the effects of load distribution and load static transmission errors. Wang and Lim et al. [14] built a numerical model and discussed the effect of gear parameters set for the dynamic response. Miyoshi [15] and Sanchez [16] developed an analytical calculation method, which is used to calculate the results of the load distribution and the contact stress with a lateral contact ratio greater than two. Cooley and Parker [17] predicted the development and technical difficulties of planetary gear dynamics and vibration. But, due to the complexity symmetrical structure of HPGS, most scholars in the above studies believe that the dynamic characteristics of the two symmetrical sides of the herringbone gear are the same. Actually, the carrier and sun gear would twist during the operation of HPGS. And the torsion of the sun gear under load will cause the flexible dislocation between the two symmetrical sides of the sun gear. This torsional flexibility of sun gear will have a direct impact on the dynamic characteristics of the HPGS. In addition, due to bearing installation clearance, manufacturing and installation errors, the meshing center points of the single helical gears on both sides of the sun gear and the planetary gear are not in the same vertical plane of geometric center. These effects cause the axial sliding between left and right meshing centers, which will change meshing stiffness and dynamic mesh force response.
In this investigation, a dynamic model of the HPGS including torsional flexibility between two symmetrical sides teeth of the sun gear is developed, based on the lumped-parameter method considering the torsional flexibility and the axial slide of the both sides teeth of the sun gear. Then, the influences of change of torsional flexibility and axial slide of the both sides teeth of the sun gear on the dynamic parameters and dynamic characteristics for the HPGS are discussed.
2 Dynamic model of the HPGS
2.1 Basic parameters and dynamic model of the HPGS
A typical HPGS is shown in Figure 1. Blades are used as input to provide power for the transmission system. And the generator sets convert kinetic energy into electrical energy. The input torque is transferred to the planetary gears from the carrier, afterwards to sun gear shaft by herringbone planetary train, then to parallel transmission stage by the sun gear shaft, and finally to the generator set. The rated input power of the HPGS are 1.5 MW. The material of all gears is 20CrMnMo6. And the surfaces of all gears are carburized. The symbol of the HPGS is defined as follows: r denotes the ring gear, and c means the carrier, and s represents the sun gear, and pn represents the nth planet gears, of which (n = 1, 2, 3, 4). When the subscript i equals L, it means the left side of the herringbone gear. When the subscript i equals R, it indicates the right side of the herringbone gear. The structural parameters of the research object are illustrated in Table 1.
Dealing with the intermediate shaft section of herringbone gear is a very critical issue. In the process of dynamic modeling of the herringbone gear transmission system at home and abroad, in order to more accurately simulate the coupling between the structures, the herringbone gear is equivalent to the double helical gears on the left and right sides based on the three-piece model [18,19]. Under the beam theory that only considers torsion, a herringbone gear is divided into three pieces: same inner diameter on left and right sides gear segment, and a connecting structure, which spans from gear face mid-point from the left side OL to the right side OR. The mass and moment of inertia concentrate on the adjacent nodes OL and OR respectively. Relief groove part is equivalent to the torsion beam elements with two nodes. The joints nodes OL and OR are at the beginning and end of the beam element respectively. The equivalent support stiffness and damping of the left and right support bearings of herringbone gear act on two nodes OL and OR respectively. Here, the relevant dynamic characteristic parameters are obtained by changing the torsional flexibility of the both sides tooth of the sun gear. lLR is the distance from point OL to OR, which is the distance between the centers of the left and right single helical gears, and lLT is the distance from point OL to OT, which is 657.5mm, and lRT is the distance from point OR to OT, which is 432.5 mm. Figure 2 illustrates equivalent model of herringbone gear middle segment. Figure 2a shows three-piece model of herringbone gear. Figure 2b illustrates the schematic diagram of the beam element.
According to Figure 2, relative torsion and bending angle can be obtained by torsion beam element. Sun gear and planet gears are regarded as two single helical gears connected together, and each helical gear owns four degrees of freedom, comprising translational movements in the three directions of x, y, and z axes, and a rotation around the z-axis. Therefore, only relative torsion angle is considered in the dynamic model. And relative torsion angle is inversely proportional to the torsional stiffness of the equivalent middle shaft segment lLR, the parameter φLj is the relative torsion angle of the left single helical gear. Correspondingly, φRj is the relative torsion angle of the right side. The relative torsion angle φLRj of two single helical gears between φLj and φRj of the sun gear is expressed as equation (1). (1)where Ts denotes the external load on the sun gear, torsional stiffness Kj = GjIj, and the shear elastic modulus G = E/(2(1+ν)), E is the elastic modulus, E = 206 Gpa, and ν = 0.3, Ij is the torsional moment of inertia.
(1)where Ts denotes the external load on the sun gear, torsional stiffness Kj = GjIj, and the shear elastic modulus G = E/(2(1+ν)), E is the elastic modulus, E = 206 Gpa, and ν = 0.3, Ij is the torsional moment of inertia.
According to equation (1), when the sun gear is applied with a constant external load, the torsional flexibility of the two symmetrical sides of the sun gear is determined by Kj and l. Of course, the axial slide of the sun gear will affect the torsional flexibility between the both sides teeth of the sun gear.
The displacement of the beam element in the local coordinate system is illustrated in Figure 2. The focus of this article is to consider the influence of torsional flexibility, and the torsional flexibility is mainly investigated here. Therefore, only four degrees of freedom are considered in the single helical gear, comprising translational movements in the three directions of x, y, and z axes, and a rotation around the z-axis. And the specific expression of the displacement vector of the equivalent double-helical gear system is shown in equation (2).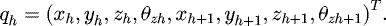 (2)
(2)
The mass and moment of inertia of each part in the equivalent double-helical gear system are distributed according to the principle that the total mass, the total moment of inertia and the position of the mass center are not changed, and are aggregated to the adjacent nodes L and R, respectively. The equivalent support stiffness of the left and right support bearings of herringbone gear are respectively, and acts on node L and node R. Both the beam element mass matrix Mie (i = s,p)and the stiffness matrix Kie (i = s,p) are presented as block sub-matrices [18]. (3a)
(3a)
 (3b)
(3b)
The specific form of each sub-matrix of the mass matrix Mie is as follows: (4a)
(4a)
 (4b)where mLs denotes the mass of the left single helical gears of the sun gear, and mRs represents the mass of the right single helical gear of the sun gear, rbs is the base circle radius of sun gear, ILs is moment of inertia of the left single helical gears of the sun gear, IRs is moment of inertia of the right single helical gears of the sun gear.
(4b)where mLs denotes the mass of the left single helical gears of the sun gear, and mRs represents the mass of the right single helical gear of the sun gear, rbs is the base circle radius of sun gear, ILs is moment of inertia of the left single helical gears of the sun gear, IRs is moment of inertia of the right single helical gears of the sun gear.
Using the same method, the specific form of the stiffness matrix Kie can be obtained. In order to save space, it will not be listed here.
 |
Fig. 1 Schematic diagram of HPGS. |
Structural parameters of HPGS.
 |
Fig. 2 Equivalent model of herringbone gear middle segment. (a) Three-piece model of herringbone gear. (b) Torsion beam element. |
2.2 Meshing stiffness of HPGS considering the meshing phase
According to the principle of elastic potential energy with considering the torsional flexibility of two sides teeth of sun gear, and comprehensive consideration of the effects of various factors on deformation, the single tooth meshing stiffness of s-p meshing pairs and r-p meshing pairs can be expressed as: (5)where Kb, Ks, Ka are the stiffness of deformation of bending, shear and axial, respectively, and Khz is the stiffness of Hertz contact, and subscript 1 and 2 represent driving and driven gear, respectively.
(5)where Kb, Ks, Ka are the stiffness of deformation of bending, shear and axial, respectively, and Khz is the stiffness of Hertz contact, and subscript 1 and 2 represent driving and driven gear, respectively.
There are three kinds of meshing phase differences in general planetary gears: s-p mesh, r-p mesh and between s-p and r-p mesh [6]. But, the herringbone planetary gear transmission has four meshing phases when torsional flexibility is considered. They are defined as the phase coefficient λsn, λrn, 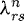 and λLRj represent the relative phase of the nth to the first s-p meshing pair, the nth to the first r-p meshing pairs, the nth s-p meshing pairs to the nth r-p meshing pair and left s-p meshing pair to right s-p meshing pair, respectively. λLRj is between left side and right side phasing difference caused by relative torsion angle φLRj.
and λLRj represent the relative phase of the nth to the first s-p meshing pair, the nth to the first r-p meshing pairs, the nth s-p meshing pairs to the nth r-p meshing pair and left s-p meshing pair to right s-p meshing pair, respectively. λLRj is between left side and right side phasing difference caused by relative torsion angle φLRj.
Δt is the time interval of the nth to the first s-p meshing pair, Tm denotes the mesh period of all phases.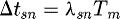 (6)
(6)
 (7)
(7)
In this dynamic model, φn represents the angle of the nth to the first planet gear on the right side. As the right sun gear rotates angle φn relative to the carrier, the right side nth planet gear moves to the position right belonging to the right side first planet gear, and the expression of the required time t is shown by the following: (8)
(8)
Uniting the equation (6) and the equation (7): (9)where pn is an integer, and the expression of λsn can be obtained by combining the equations (6) and (7).
(9)where pn is an integer, and the expression of λsn can be obtained by combining the equations (6) and (7).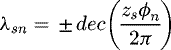 (10a)where dec(A) represents the decimal part of A, so λsn = λrn and
(10a)where dec(A) represents the decimal part of A, so λsn = λrn and  can be derived.
can be derived. (10b)
(10b)
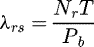 (10c)where NrT is the distance between r-pn initial meshing position point T and meshing pitch point Nr when the starting point of s-pn meshing is at meshing pitch point Ns, Pb is the planetary gear pitch.
(10c)where NrT is the distance between r-pn initial meshing position point T and meshing pitch point Nr when the starting point of s-pn meshing is at meshing pitch point Ns, Pb is the planetary gear pitch.
When considering torsional flexibility of the both sides teeth of the sun gear, (φn + φLRj) means the actual rotation angle of the left side sun gear relative to the carrier, and the phase coefficient λLRj is shown by the following: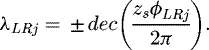 (11)
(11)
According to the equation (11), at any time t, the instantaneous total contact line length of single helical gear pair in herringbone gear is L(t) as shown by the following: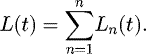 (12)
(12)
Then, according to the equation (12), the expression of tooth meshing stiffness k(t) can be derived by the following: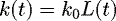 (13)where k0 is the meshing stiffness per unit contact line length.
(13)where k0 is the meshing stiffness per unit contact line length.
Therefore, considering the torsional flexibility of the both sides tooth of the sun gear, the expression of meshing stiffness of the s-p meshing pairs is shown as: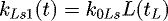 (14a)
(14a)
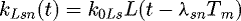 (14b)
(14b)
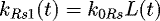 (14c)
(14c)
 (14d)
(14d)
This article only considers the torsional flexibility of the both sides tooth of the sun gear, so there is no influence on r-p meshing pairs, and the expression of its meshing stiffness is shown as: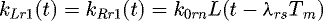 (15a)
(15a)
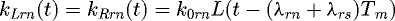 (15b)where λrs is meshing phase difference between s-p mesh and r-p mesh.
(15b)where λrs is meshing phase difference between s-p mesh and r-p mesh.
2.3 Dynamic equations of the HPGS
The dynamic model of HPGS is shown in Figure 3, Three coordinate systems are established in the above model. OXYZ expresses a static coordinate system. And their origin is the rotation center of the carrier. The x-axis through the first planet's rotation center and uses the rotation center of the carrier as the origin, which rotates at a constant speed around the z-axis with the angular velocity ωc of the carrier. onxnynzn is a moving coordinate system. The difference between onxnynzn is that onxnynzn rotates at a constant speed with carrier around the zn-axis, using the rotation center of each planetary gear as the origin.
In this dynamic model, herringbone sun gear and planet gears are regarded as two single helical gears connected together. Left and right sides of herringbone gears are assumed identical in geometry expect the hand of the teeth is opposite with respect to each other. In an actual herringbone planetary gear system, left and right sides of gears and carrier are either one-piece (for planet and sun gears) or connected rigidly (for the ring gear and carrier). Sun gear, planet gears and ring gear are regarded as two single helical gears connected together, and each helical gear owns four degrees of freedom, comprising translational movements in the three directions of x, y, and z axes, and a rotation around the z-axis. In addition, the following assumptions are made in the dynamic model: (a) without considering the energy loss, the input torque can be directly applied on the carrier, and the load torsion can directly applied on the sun gear. (b) It is assumed that the left and right sides of herringbone gear are geometrically symmetrical, and the rotation of teeth is opposite to each other. They are staggered by a certain angle with torsional flexibility of relief groove. (c) It is difficult to obtain the damping coefficient, damping of the system is represented by a constant modal damping, and the friction effect of gear pair meshing and the friction between other parts are ignored. According to the equation (16), the displacement vector q of the system is obtained. Moreover, the model of the transmission system contains 8(N + 3) degrees of freedom in total. (16)where x, y, and z denote the lateral, longitudinal and axial displacements of the component, respectively. The parameter θ denotes the angular displacement, the subscript is denotes the sun gear, the subscript in denotes the nth planet gear, r is the ring gear, and c is the carrier.
(16)where x, y, and z denote the lateral, longitudinal and axial displacements of the component, respectively. The parameter θ denotes the angular displacement, the subscript is denotes the sun gear, the subscript in denotes the nth planet gear, r is the ring gear, and c is the carrier.
Figure 4 illustrates the relative positional relationship of the components of the HPGS. The left side relative displacements of the s-p and r-p meshing pairs perpendicular to the tooth surface can be obtained from Figure 4. The right side relative displacements are symmetrical with left side.
Before calculating the relative displacement of the herringbone tooth, this paper takes the herringbone gear quivalent to two identical single helical gears on the left and right sides respectively. Therefore, the relative displacement of the left and right sides needs to be calculated separately. Taking the calculation of the left-side relative displacement of the sun gear and the planet gear as an example, the solution process will be introduced in detail.
Projecting the displacement of the sun gear and planetary gear in the x direction onto the meshing plane s-n to obtain xLs sin ψsn and xLn sin ψsn. Since the sun gear and the planet gear rotate in opposite directions, the displacement projections of the sun gear and the planet gear on the meshing line in the x direction are (− xLs sin ψsn cos βLb) and xLn sin ψsn cos βLb, respectively. Therefore, the comprehensive relative displacement of the sun gear and planetary gear in the x direction is (xLn − xLs) sin ψsn cos βLb. Using the same method, the projections (yLs − yLn) cos ψsn cos βLb and (zLs + zah − zLn) sin βLb of the displacements in the y-direction and z-direction of the sun gear and planetary gears on the meshing line can be obtained, respectively. Due to torsion flexibility and manufacturing and installation errors, the projection [rbs(θLs + φh) + rbpθLn] cos βLb of the torsional freedom and the transmission error eLsn need to be added. Therefore, we can easily get the equation (17a).
Using the same method, we can obtain the following equations (18) and (19). Therefore, δLsn and δLsn represent the relative meshing displacement of the s-p mesh in the direction normal to tooth surface such that [18]: (17a)
(17a)
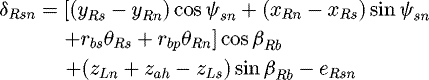 (17b)
(17b)
Relative displacement between ring gear and planet gears is: (18)
(18)
Relative displacement of the planet gear to the carrier is: (19a)
(19a)
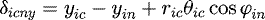 (19b)
(19b)
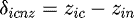 (19c)
(19c)
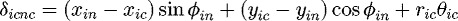 (19d)where ψsn = ϕsp − αn, ψrn = ϕrp + αn, rbs, rbp and rbr represent the radius of the base circle of the sun, planet, and ring gears, respectively, and rc denotes the distance from the center of planet gear to rotation center of carrier, and ϕ represents the transverse pressure angle, αn represents the position angle belonging to nth planet gears, βib denotes the helix angle of the single helical gear on two symmetrical sides of the herringbone gears, and za represents the axial slide of the sun gear, eisn and einr denote respectively the transmission error on the nth s-p and r-p meshing pairs.
(19d)where ψsn = ϕsp − αn, ψrn = ϕrp + αn, rbs, rbp and rbr represent the radius of the base circle of the sun, planet, and ring gears, respectively, and rc denotes the distance from the center of planet gear to rotation center of carrier, and ϕ represents the transverse pressure angle, αn represents the position angle belonging to nth planet gears, βib denotes the helix angle of the single helical gear on two symmetrical sides of the herringbone gears, and za represents the axial slide of the sun gear, eisn and einr denote respectively the transmission error on the nth s-p and r-p meshing pairs.
To reflect the dynamic characteristics of the HPGS more truly, this model considers the torsional flexibility of the both sides tooth of the sun gear. The dynamic equations of the single helical gear on the left and right sides of the sun gear can be determined as follows: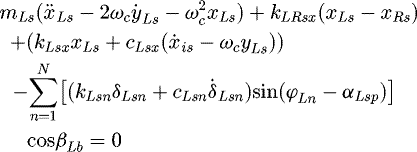 (20a)
(20a)
 (20b)
(20b)
 (20c)
(20c)
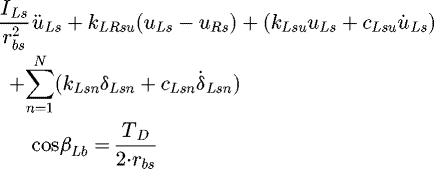 (20d)
(20d)
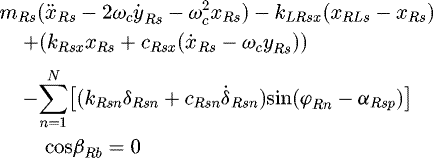 (21a)
(21a)
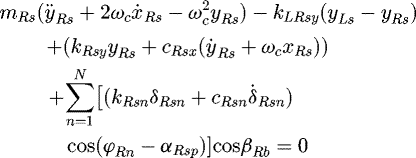 (21b)
(21b)
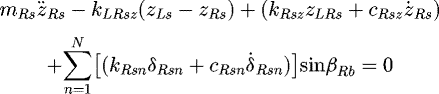 (21c)
(21c)
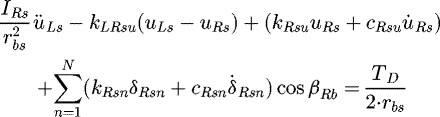 (21d)where mLs denotes the mass of the left single helical gears of the sun gear, and mRs represents the mass of the right single helical gear of the sun gear, ς is the three translational motions of freedom along the x, y and z directions, and a rotation around z-axis, TD represents input and output torque, kLRsς is the stiffness on the ς direction between the two symmetrical sides single helical gear of the sun gear, kisς and cisς denote the support stiffness and support damping of the sun gear along the ς direction, kisn and cisn denote the meshing stiffness and mesh damping between the nth planet gears and the sun gear, respectively.
(21d)where mLs denotes the mass of the left single helical gears of the sun gear, and mRs represents the mass of the right single helical gear of the sun gear, ς is the three translational motions of freedom along the x, y and z directions, and a rotation around z-axis, TD represents input and output torque, kLRsς is the stiffness on the ς direction between the two symmetrical sides single helical gear of the sun gear, kisς and cisς denote the support stiffness and support damping of the sun gear along the ς direction, kisn and cisn denote the meshing stiffness and mesh damping between the nth planet gears and the sun gear, respectively.
Equations of motion of the components ring gear, carrier and the planets can be derived in a similar way. The 8(N + 3) DOF coupled dynamic equations can then be derived through the coordination of the rotation angles and the balance of the torques. The dynamic equations of the HPGS are arranged into a matrix modus as follows: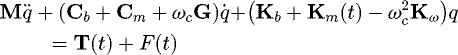 (22)where C
b is the matrix of support damping, and C
m represents the matrix of meshing damping, and G denotes the matrix of gyroscopic, and M represents the mass matrix belonging to the system, and ωc expresses the angular speed belonging to the carrier, and K
b denotes matrix of the support stiffness, and K
m means the matrix of meshing stiffness, and Kω represents the matrix of the centripetal stiffness, and T expresses the torque vector, and F(t) is individual force vector caused by transmission error and time-varying meshing stiffness.
(22)where C
b is the matrix of support damping, and C
m represents the matrix of meshing damping, and G denotes the matrix of gyroscopic, and M represents the mass matrix belonging to the system, and ωc expresses the angular speed belonging to the carrier, and K
b denotes matrix of the support stiffness, and K
m means the matrix of meshing stiffness, and Kω represents the matrix of the centripetal stiffness, and T expresses the torque vector, and F(t) is individual force vector caused by transmission error and time-varying meshing stiffness.
The equations of the dynamic mesh force response of sun gear and planet gear, ring gear and planet gear as follows: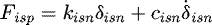 (23a)
(23a)
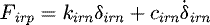 (23b)where Fisp denotes the dynamic mesh force response of s-p meshing pairs, and Firp represents the dynamic mesh force response of r-p meshing pairs, and kisn represents the meshing stiffness of s-p meshing pairs, and kirn denotes the meshing stiffness r-p meshing pairs, and cisn is the mesh damping of s-p meshing pairs, and cirn is the mesh damping of r-p meshing pairs.
(23b)where Fisp denotes the dynamic mesh force response of s-p meshing pairs, and Firp represents the dynamic mesh force response of r-p meshing pairs, and kisn represents the meshing stiffness of s-p meshing pairs, and kirn denotes the meshing stiffness r-p meshing pairs, and cisn is the mesh damping of s-p meshing pairs, and cirn is the mesh damping of r-p meshing pairs.
 |
Fig. 3 Dynamic model of the HPGS. |
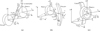 |
Fig. 4 Left side positional relationship diagram of the HPGS. (a) Sun-planet mesh. (b) Ring-planet mesh. (c) Carrier-planet. |
3 Influence analysis of meshing parameters
3.1 Influence on the time-varying meshing stiffness
In order to study the influence of torsional stiffness of sun gear on meshing stiffness, a series of meshing stiffness kisn of the system can be obtained under different torsional stiffness according to equations (14) and (15). The initial torsional stiffness between the both sides teeth of the sun gear is 5.2 × 107 N m2 based on the equation (1). Here, the variation of torsional stiffness changes from 5.2 × 107 N m2 to 4.0 × 107 N m2. The torsional stiffness K1, K2, K3, K4, K5 are 5.2 × 107 N m2, 4.9 × 107 N m2, 4.6 × 107 N m2, 4.3 × 107 N m2, 4.0 × 107 N m2.
Figure 5a and 5b show the trend of meshing stiffness in case of the changing the torsional stiffness from K1 to K5. As the torsional stiffness Kj decreases, the meshing stiffness of the left side s-p meshing pairs increases, while the right meshing pair is opposite. When the torsional stiffness of the sun gear decreases from 5.2 × 107 N m2 to 4.0 × 107 N m2, the maximum meshing stiffness of left s-p meshing pairs is increases by 9.79%, and the right side decreases by 11.23%.
To analyze the influence of axial slide of the sun gear on time-varying meshing stiffness, left and right sides of s-p meshing stiffness are calculated in case of −0.5 mm, 0 mm, +0.5 mm and +1 mm, respectively. The direction of slide is indicated by ‘+’ means sun gear slides towards the right (to output direction). The meshing stiffness of the s-p meshing pairs under the sun gear axially sliding are shown in Figure 6.
According to Figure 6, when the sun gear slides 1mm to the right under the initial torsional stiffness K1, the maximum meshing stiffness of the left side s-p meshing pairs decreases 6.30 × 107 (N/m), and the right side s-p meshing pairs increases 1.11 × 108 (N/m). From the point of view of time-varying meshing stiffness, when the sun gear slides axially, the time-varying meshing stiffness of s-p meshing pairs could be adjusted by adjusting the torsional flexibility of the two sides teeth of the sun gear.
Then, according to equations (22) and (23), the dynamic gear meshing force time history for the left side and right side of s-p1 meshing are obtained at mesh frequencies 1440Hz. When the torsional flexibility is rigid, the herringbone planetary gear can be considered to be completely symmetrical on the left and right, which is equivalent to spur gear. Parker's model [1] can be used to compare the dynamic meshing force to verify the model. For comparison, the dynamic load factor 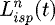 is defined to represent the dynamic load sharing time history among the planets gear as equation (24).
is defined to represent the dynamic load sharing time history among the planets gear as equation (24).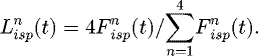 (24)
(24)
In fact, when torsional flexibility is not considered, the axial load of herringbone planetary gear offsets each other, and the model is very similar to the Parker's spur planetary gear model. But in this model, the herringbone gear is equivalent to the double helical gears on the left and right sides, and the direction of helix angle is opposite. And due to the torsional flexibility of herringbone planetary gear, the dynamic mesh force of left and right single helical gears is different. Figure 7 show the dynamic load factor time history of s-p mesh, including both sides s-p1 mesh and s-p1 mesh of equivalent Parker's model. From Figure 8, the maximum dynamic load factor on the left is 1.04, and right side is 1.03. They are slightly different, but are very close to 1.09 of Parker's model. In terms of the overall trend, Parker's model is very close to the dynamic load factor curve of s-p on the right side of this article, and is slightly different from the left side. The results are a good agreement with the Parker's model results.
 |
Fig. 5 Left and right sides meshing stiffness of the s-p mesh with changing torsional stiffness. (a) Left side s-p mesh cycle. (b) Right side s-p mesh cycle. |
 |
Fig. 6 Left and right sides meshing stiffness of s-p mesh with sun gear axially sliding. |
 |
Fig. 7 Dynamic load factor time history of s-p1 mesh. |
 |
Fig. 8 Unit length load (N/mm) of tooth surface with torsional stiffness and axial sliding. (a) Left side with K1. (b) Right side with K1. (c) Left side with K5. (d) Right side with K5. (e) Left side with +1 mm axially sliding and K1. (f) Right side with +1 mm axially sliding and K1. |
3.2 Influence of torsional flexibility on tooth surface load
Tooth surface load is an important index that reflects the gear tooth meshing contact performance. References [14,15] used the slice method in the axial direction for gears and analyzed the distribution of the tooth surface load of helical gears by considering various factors. The general expression for total load and total deformation of gear teeth can be obtained as: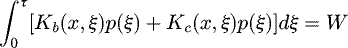 (25)
where Kb(x, ξ) and Kc(x, ξ) represent the influence coefficient of the bending and contact deformation of the gear teeth, respectively. p(ξ) represents the distributed load on the gear contact line, W represents total meshing deformation, τ represents the total contact line length.
(25)
where Kb(x, ξ) and Kc(x, ξ) represent the influence coefficient of the bending and contact deformation of the gear teeth, respectively. p(ξ) represents the distributed load on the gear contact line, W represents total meshing deformation, τ represents the total contact line length.
The sun gear tooth surface unit length load distributions are achieved for changing torsional stiffness from K1 to K5. Figure 8 shows the trend of unit length load of the tooth surface with torsional stiffness and axial sliding of sun gear.
According to Figure 8, the distributions of tooth surface load of the left and right s-p meshing pairs are not completely the same. When the torsional stiffness K1 equals 5.2 × 10−5 rad, the maximum load area of the left s-p meshing pairs is 880N/mm, and the minimum load area is 260 N/mm, and the maximum load area of the right s-p meshing pairs is 850 N/mm, and the minimum load is 270 N/mm. When the torsional stiffness K1 equals 4.0 × 107 N m2, the maximum load area of the left s-p meshing pairs is 940 N/mm, and the minimum load area is 280 N/mm, and the maximum load area of the right s-p meshing pairs is 780 N/mm, and the minimum load area is 240 N/mm. The maximum load area of the left side s-p meshing pairs increases by 6.82%, but the right side decreases by 8.34%.
The same method can be used to obtain the tooth surface load distribution of the s-p meshing pairs under the sun gear sliding axially as shown in Figure 8e and 8f. When the sun gear slides to the right by 1mm under the initial torsional stiffness K1. The maximum load area of the left s-p meshing pairs is 790 N/mm, and the minimum load area is 250 N/mm, and the maximum load area of the right s-p meshing pairs is 940 N/mm, and the minimum load area is 280 N/mm. The maximum load area of the left side s-p meshing pairs decreases by 10.20%, but the right side s-p meshing pairs increases by 10.59%.
4 Effects of torsional flexibility and axial sliding on dynamic mesh force
In the HPGS, the dynamic mesh force is the main index of dynamic characteristics. Thus, the dynamic force response of the HPGS can be analyzed by changing torstional stiffness and axial sliding. Steady-state responses are obtained by using the fifth-order variable step-size Runge-Kutta method to solve the dynamic equation (22). Then the continuous frequency sweep method is used to analyze the dynamic mesh force response of the HPGS. In continuous frequency sweep, the frequency change is realized by continuous changing the meshing period. The steady-state response speed at the end of the previous sweep step is used as the initial condition for the next frequency sweep step. Here the amplitude of the response is the root-mean-square values of the dynamic mesh forces. At last, the left and right sides dynamic mesh force response Fisp of the s-p mesh are conducted with different torsional stiffness and axial sliding of the sun gear.
Figure 9 shows the left and right sides dynamic mesh force response curves of the s-p mesh are conducted by the s-p mesh frequency sweep from 0 Hz to 5000 Hz, and the torsional stiffness of sun gear is chosen from K1 = 5.2 × 107 N m2 to K5=4.0 × 107 N m2. It can be seen from Figure 9a and 9b, the s-p meshing pair has almost no change in dynamic mesh force response at low frequencies, and the resonance peak of the most obvious frequency change appears near the frequency of 1440 Hz and 2500 Hz. With the increase of torsional flexibility, both the dynamic mesh force response peak values and peak frequencies of the left and right s-p meshing pairs decrease very obviously. Therefore, appropriate increasing the torsional flexibility of the both sides tooth of the sun gear can reduce the main peak values and peak frequencies of the s-p meshing pairs significantly, which will alleviate the vibration conditions of the system.
In order to observe the sun gear axially sliding on dynamic mesh force response, a group of axially sliding cases are employed to sweep the dynamic mesh force response. These axially sliding cases include 0 mm, +0.5 mm, +1 mm under initial torsional stiffness K1, and +1 mm under torsional stiffness K5, respectively. The dynamic mesh force response of the s-p meshing pairs with the sun gear axially sliding can be shown in Figure 10.
According to Figure 10, when sun gear axially sliding changes from 0 to +1mm to the right side, the left dynamic mesh force response peak decreases and the right response peak increases. The most obvious frequency change appears near the frequency of 1440 Hz and 2500 Hz. But both sides peak frequencies have almost no change when only axial sliding is applied. In addition, axial sliding and torsional stiffness are both applied, both sides response peak and response peak frequencies are still obviously decreased.
 |
Fig. 9 Frequency sweep of dynamic mesh force with changing torsional stiffness. (a) Left side s-p mesh. (b) Right side s-p mesh. |
 |
Fig. 10 Dynamic mesh force response under sun gear axially sliding. (a) Left side s-p mesh. (b) Right side s-p mesh. |
5 Conclusion
This investigation takes the HPGS as the research object, mainly analyzing influence of the meshing stiffness, the tooth surface load and the dynamic mesh force of the HPGS under the changing of the torsional stiffness and the axial slide of the sun gear. Combining the structural characteristics of herringbone gears, a novel dynamic model of the HPGS is developed based on a lumped parameter method. The conclusions show that, as the torsional stiffness of the both sides tooth of sun gear decreases, the meshing stiffness and maximum load area of the left side s-p meshing pair increase and the right side decrease, the dynamic mesh force response peak values of the left and right s-p meshing pairs in all frequencies decrease, and peak frequencies of the main peak values decreases. When the sun gear slides to the right, the meshing stiffness, maximum load area and dynamic mesh force of the left side s-p meshing pairs decrease, while the right side s-p meshing pairs increase, but peak frequencies keep the same. The results could be applied to reduce vibration and impact of the system, prolong the service life.
Nomenclature
Cb: The support damping matrix
Cm: The meshing damping matrix
cisς: The support damping of the sun gear on the ζ direction
cisn: The meshing damping of the nth sun to planet meshing pairs
F(t): The dynamic exciting force
Firp: Dynamic mesh force of the nth ring to planet meshing pairs
Fisp: Dynamic mesh force of the nth sun to planet meshing pairs
Gj: Modulus of elasticity in shear
Ij: Torsional moment of inertia
ILs: Moment of inertia of the left single helical gears of the sun gear
IRs: Moment of inertia of the right single helical gears of the sun gear
Kb: The matrix of support stiffness
Km: The meshing stiffness matrix
Kω: The centripetal stiffness matrix
Kie: The stiffness matrix of beam element
Khz: The stiffness of Hertz contact
Kj: Torsional stiffness between the two sides teeth of sun gear
Km: The meshing stiffness of meshing single pair
Kb, Ks, Ka: The stiffness of deformation of bending, shear and axial, respectively
Kb(x, ξ): The gears bending deformation coefficient
Kc(x, ξ): The gears contact deformation coefficient
k0: Meshing stiffness per unit contact line length
kLRsς: The stiffness in the ζ direction between the single helical gears on both sides of the sun gear
kisn: The meshing stiffness of the sun to nth planet
kisς: The support stiffness of the sun gear on direction ζ
L(t): The instantaneous total contact line length of single helical gear pair in herringbone gear
l: The length of the shaft segment from torsion center
Mie: The mass matrix of torsion beam element
mLs: The mass of the left single helical gears of the sun gear
mRs: The mass of the right single helical gear of the sun gear
N : Number of meshing teeth pairs
Nr, Ns: Meshing pitch point of r-pn and s-pn, respectively
n1: The speed of the driving gear
p(ξ): The load distribution on contact line
q : Forced vibration response vector
qh: Forced vibration response vector of the beam element
r-p : Meshing pair of ring gear to planet gear
r1: The base circle radius of the driving gear
rc: The distance from the center of planet gear to rotation center of carrier
rbζ: The base circle radius of gear ζ (ζ=s, r, pn)
s-p : Meshing pair of sun gear to planet gear
TD: The input and output torque
Tm: The mesh period of all phases
Ts: The external load on the sun gear
Δt : The time interval of the nth to the first s-p meshing pair
x : The x direction displacement of the component
y : The y direction displacement of the component
z : The z direction displacement of the component
αn: Position angle for planet n
δ : Relative mesh displacement
θ : The angular displacement of the component
ψ : Angle made by plane of action with vertical y axis
φn: Relative angle of nth planet gear on the right rotates to the position of the first planet gear
τ : The total contact line length
Subscripts
h : The hth node of herringbone gear middle segment torsion beam element
i : Left or right side of herringbone gear (i = L, R)
j : A value of torsional flexibility or torsional stiffness (j = 1,2,3,4,5)
L : Left side of herringbone gear
R : Right side of herringbone gear
ς : Translational along x, y and z axis or angular displacement around the z axis
Acknowledgments
This research is supported by the Foundation of the National Key Research and Development Plan of China (No. 2018YFB2001300), the Foundation of National Natural Science of China (No. 51975078, No. 51975079) and the Natural Science Foundation Project of Chongqing (No. cstc2018jcyjAX0087).Scientific Research Key Fund of Chongqing Municipal Education Commission (No. KJZD-K202000703).
References
- J. Lin, R.G. Parker, Analytical characterization of the unique properties of planetary gear free vibration, J. Vib. Acoust. 15 , 316–321 (1999) [Google Scholar]
- L.L. Zhang, R.P. Zhu, Impact of meshing phase on load sharing for herringbone planetary train, J. Mech. Eng. 54, 129–140 (2018) [Google Scholar]
- P. Sondkar, A. Kahraman, A dynamic model of a double-helical planetary gear set, Mech. Mach. Theory 157–174 (2013) [Google Scholar]
- Z.H. Bu, G. Liu, L.Y. Wu, Modal analyses of herringbone planetary gear train with journal bearings, Mech, Mach. Theory 54 , 99–115 (2012) [CrossRef] [Google Scholar]
- C.C. Zhu, X.Y. Xu, H.J. Liu et al., Research on dynamical characteristics of wind turbine gearboxes with flexible pins, Renew. Energy 68 , 724–732 (2014) [Google Scholar]
- C.C. Zhu, X.Y. Xu, T.C. Lim et al., Effect of flexible pin on the dynamic behaviors of wind turbine planetary gear drives, Proc. Inst. Mech. Eng. C 227 , 74–86 (2013) [CrossRef] [Google Scholar]
- C. Wang, S.R. Wang, G.Q. Wang, Research on dynamic model of double helical gear pair based on TCA and LTCA, Int. J. Acoustics Vib. 24 , 476–484 (2019) [CrossRef] [Google Scholar]
- F. Wang, X. Xu, Z.D. Fang et al., Design and analysis of herring-bone gear with sixth-order transmission error based on meshing vibration optimization, Adv. Mech. Eng. 9 (2017) [Google Scholar]
- S. Mo, Y.D. Zhang, Q. Wu et al., Research on natural characteristics of double-helical star gearing system for GTF aero-engine, Mech. Mach. Theory 106 , 166–189 (2016) [Google Scholar]
- S. Mo, T. Zhang, G.G. Jin et al., Dynamic characteristics and load sharing of herringbone wind power gearbox, Math. Probl. Eng. (2018) [Google Scholar]
- C.Z. Liu, D.T. Qin, T.C. Lim et al., Dynamic characteristics of the her-ringbone planetary gear set during the variable speed process, J. Sound Vib. 333 , 6498 –6515 (2014) [Google Scholar]
- F. Ren, G.F. Luo, G.Q. Shi, Influence of manufacturing errors on dynamic floating characteristics for herringbone planetary gears, Nonlinear Dyn. 93 , 361–372 (2018) [Google Scholar]
- Z. Chen, Y. Shao, Meshing stiffness calculation of a spur gear pair with tooth profile modification and tooth root crack, Mech. Mach. Theory 62 , 63–74 (2013) [Google Scholar]
- J.H. Wang, T.C. Lim, L.D. Yuan, Spur gear multi-tooth contact dy-namics under the influence of bearing elasticity and assembly errors, Proc. Inst. Mech. Eng. C 227 , 2240–2455 (2013) [Google Scholar]
- Y. Miyoshi, K. Tobisawa, K. Saiki, Composite analysis method of tooth contact load distribution of helical gear, in ASME 2007 Inter-national Design Engineering Technical Conferences and Com-puter and Information in Engineering Conference, American So-ciety of Mechanical Engineers, 2013, 173–180 [Google Scholar]
- M.B. Sanchez, J.I. Pedrero, M. Pleguezuelos, Contact stress calcu-lation of high transverse contact ratio spur and helical gear teeth, Mech. Mach. Theory 64 , 93–110 (2013) [Google Scholar]
- C.G. Cooley, R.G. Parker, A review of planetary and epicyclic gear dynamics and vibrations research, Appl. Mech. Rev. 66 , 040804 (2014) [Google Scholar]
- P. Sondkar, Dynamic modeling of double-helical planetary gear sets, The Ohio State University, Athens, 2012 [Google Scholar]
- B. Yuan, S. Chang, G. Liu, L. Liu, L.D. Jiang, Analysis of dynamic characteristics of herringbone gear system considering cumulative error of tooth pitch, Vib. Shock 39 , 120–112 (2020) [Google Scholar]
Cite this article as: X. Xu, H. Ge, J. Deng, J. Wang, R. Chen, An investigation on dynamic characteristics of herringbone planetary gear system with torsional flexibility between the left and right teeth of the sun gear, Mechanics & Industry 21, 602 (2020)
All Tables
All Figures
 |
Fig. 1 Schematic diagram of HPGS. |
| In the text | |
 |
Fig. 2 Equivalent model of herringbone gear middle segment. (a) Three-piece model of herringbone gear. (b) Torsion beam element. |
| In the text | |
 |
Fig. 3 Dynamic model of the HPGS. |
| In the text | |
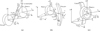 |
Fig. 4 Left side positional relationship diagram of the HPGS. (a) Sun-planet mesh. (b) Ring-planet mesh. (c) Carrier-planet. |
| In the text | |
 |
Fig. 5 Left and right sides meshing stiffness of the s-p mesh with changing torsional stiffness. (a) Left side s-p mesh cycle. (b) Right side s-p mesh cycle. |
| In the text | |
 |
Fig. 6 Left and right sides meshing stiffness of s-p mesh with sun gear axially sliding. |
| In the text | |
 |
Fig. 7 Dynamic load factor time history of s-p1 mesh. |
| In the text | |
 |
Fig. 8 Unit length load (N/mm) of tooth surface with torsional stiffness and axial sliding. (a) Left side with K1. (b) Right side with K1. (c) Left side with K5. (d) Right side with K5. (e) Left side with +1 mm axially sliding and K1. (f) Right side with +1 mm axially sliding and K1. |
| In the text | |
 |
Fig. 9 Frequency sweep of dynamic mesh force with changing torsional stiffness. (a) Left side s-p mesh. (b) Right side s-p mesh. |
| In the text | |
 |
Fig. 10 Dynamic mesh force response under sun gear axially sliding. (a) Left side s-p mesh. (b) Right side s-p mesh. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


