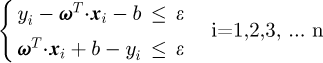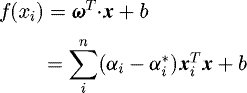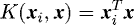| Issue |
Mechanics & Industry
Volume 22, 2021
|
|
|---|---|---|
| Article Number | 29 | |
| Number of page(s) | 9 | |
| DOI | https://doi.org/10.1051/meca/2021028 | |
| Published online | 14 April 2021 | |
Regular Article
Wear assessment model for cylinder liner of internal combustion engine under fuzzy uncertainty
1
School of Mechanical and Precision Instrument Engineering, Xi'an University of Technology, Xi'an 710048, PR China
2
School of Printing, Packaging Engineering and Digital Media Technology, Xi'an University of Technology, Xi'an 710048, PR China
* e-mail: yanjunlu@xaut.edu.cn
Received:
28
September
2020
Accepted:
29
March
2021
The wear of the piston ring-cylinder system is inevitable in the operation of the internal combustion engines (ICEs). If wear exceeds the maximum, the piston ring-cylinder system will be failure. A novel wear assessment model is proposed based on the support vector regression, and the fuzzy uncertainty is modeled to describe the random behavior under small sample. To verify the proposed model, the sample data of cylinder liner wear is applied. For best results, the particle swarm optimization (PSO) algorithm is used to optimize the model parameters. A back propagation neural network (BPNN) is employed to verify the effectiveness of the proposed model. The results show that the novel support vector regression has better prediction accuracy than other methods for cylinder wear in this paper, the proposed model can evaluate the cylinder liner wear of the ICEs effectively. The work provides a technical support for evaluating the service performance of the piston ring-cylinder liner and a reference for regular maintenance of the ships.
Key words: Wear assessment / cylinder liner / support vector regression / fuzzy uncertainty / particle swarm optimization algorithm
© J. Kang et al., Published by EDP Sciences 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The piston ring-cylinder liner system is the core component of high-performance internal combustion engines. The wear of the piston ring-cylinder liner system effects the energy transformation, and reduces the reliability of the ICEs. Therefore, how to effectively reduce the wear rate, monitor and assess the wear of cylinder liner are great significance to service performance of the ICEs.
In the operational process of the ICEs, the wear of piston ring-cylinder liner system has a significant influence on energy conversion. According to the references, the friction of piston ring-cylinder liner could account about 50 percent of the total mechanical friction of an internal combustion engine [1–3]. In order to obtain the better tribological performance, the scholars are focusing on establishing friction and wear model to investigate the relationship between friction and energy consumption of the ICEs [4–8], and the effect of lubrication on friction of piston rings-cylinder liner was studied [9,10]. To monitor the wear state, some scholars analyzed the wear information of abrasive particles in the oil, and the wear of the ICEs was evaluated [11–14]. In the above works, the most scholars focused on system's friction and wear of piston ring-cylinder liner. The wear of the cylinder liner directly increases the clearance from piston ring to cylinder liner, and it also influences on the lubrication, seal, surface topography, piston secondary motion between piston ring and cylinder liner. These factors have a strong impact on the efficiency, life and reliability of the ICEs. Therefore, it is necessary to monitor the wear of the cylinder liner to improve reliability of the piston ring-cylinder liner system. Nevertheless, it is difficult to collect a large number of wear data in a short term. In 2007, Giorgio et al. [15] presented a method to calculate the reliability of cylinder liner, the cumulative damage model was established to describe the wear process. By estimating the reliability of cylinder liner, the inspection and replacement of cylinder liner can be punctually conducted to reduce the extra expense loss. Subsequently, Giorgio et al. [16–19] established a state dependent wear model, age and state dependent Markov model and Bayesian estimation model to predict the degradation process of the cylinder liner. They have done a lot of outstanding work in the degradation performance and reliability of the cylinder liner wear. Meanwhile, the fuzzy set and the failure mode, effects, and criticality analysis (FMECA) methods were used to analyze the reliability of the diesel engine turbocharger [20], the expert knowledge was introduced into their model. Through analysis and calculation, the authors provided a new method to predict the reliability of the diesel engine turbocharger. In the references [15–20], the most scholars established the model of cylinder liner wear to research the degradation process. However, the uncertainty factors are not considered into the operational process of diesel engine, which have great influence on wear of cylinder liner. Chang et al. [21] proposed a calculation model to predict the life distribution of pneumatic cylinders using the performance degradation data. To predict the wear process of cylinder liner, a stochastic model was established, and a maintenance plan was developed by predicting model [22]. Zhang et al. [23] proposed a jump diffusion process with non-homogeneous compound Poisson process to model the degradation process with randomly occurring jumps, a numerical example was used to validate the effectiveness of the proposed method. Based on the small sample data of wear, Wiederkehr et al. [24] presented a new point-based approach for modeling the grain wear of tool.
In recent years, the machine learning algorithm and statistical methods are developed rapidly, and it is widely used to predict the wear of the equipments [25,26]. The fault tree analysis (FTA) and failure mode and effects analysis (FMEA) method was used to analyze the reliability of the engines, and the Artificial Neural Network (ANN) was used to predict the characteristic parameters of exhaust gas temperatures of main engine cylinders [27]. Kong et al. [28] presented a hidden semi-Markov model (HSMM) method to estimate the tool wear in milling process. The experiments showed that the proposed method can achieve higher accuracy in tool wear evaluation. In their works, the kernel principal component analysis (KPCA) technique was used to reduce the effect of noise. The Gaussian process regression (GPR) and relevance vector machine (RVM) were used for predicting the tool wear [29,30]. The above works provided the effective methods for wear prediction in industry, and the wear characteristics of the piston-cylinder liner system are similar to the tool wear, it can provide the reference for the cylinder liner. The support vector machine (SVM) has a great advantages in solving small sample, non-linear and high-dimensional problems. Considering the characteristics of the wear, the SVM is suitable for diagnosis and prediction the wear of the cylinder liner. In reference [31], the condition monitoring method for on-machine tool was proposed and the support vector regression (SVR) was used to predict the cutting tool of the flank wear. Zhang et al. [32] used SVR to predict wear volume at the running-in, the optimization method was used to obtain the optimal results of different parameters. For predicting the wear rate, an ANN-SVR model was developed [33], and the results showed the proposed model has a superior performance than ANN model. The integrated model was established to predict the wear and remaining life of the tool based on the SVR [34], and the relationship between the signal characteristic quantity and the tool wear was also studied. Zhang et al. [35] established a parameter prediction model of surface topography before and after running-in, the SVM was adopted to simulate the wear process.
In the ICEs, the wear information is closely related to the tribological, dynamic characteristics and operational condition of the piston-cylinder liner system. Therefore, the wear capacity shows the uncertainty characteristics. In this paper, a SVR-based model is proposed to predict the cylinder liner wear. In order to predict the wear effectively, a novel fuzzy-SVR model is proposed to assess the wear by incorporating the uncertainty information into the proposed model. To achieve the optimum results, the PSO algorithm is used to optimize the model parameters. BPNN is employed to compare with the proposed model for verification of the effectiveness. The numerical results showed that the proposed model can predict cylinder liner wear effectively.
2 Theoretical analysis
2.1 The SVR model
The SVM is based on the principle of structural risk minimization, it has a good generalization ability of learning model. More importantly, it can deal with the small sample data well. As a branch of the SVM, the main purpose of SVR is to fit a reasonable structural model by collecting data. The theories of the SVR are as follows: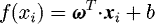 (1)
(1)
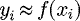 (2)where ω is the weight vector, xi is the input variable matrix, b is the bias. yi is the target value, f (xi) is the predicted value. The f (xi) is the unknown function, which depends on the sample data. If the sample data within two hyperplanes (see in Fig. 1), the error can be ignored. It can be expressed as
(2)where ω is the weight vector, xi is the input variable matrix, b is the bias. yi is the target value, f (xi) is the predicted value. The f (xi) is the unknown function, which depends on the sample data. If the sample data within two hyperplanes (see in Fig. 1), the error can be ignored. It can be expressed as
where ε is the precision. Through the above analysis, the regression problem can be transformed into minimizing problem of an empirical risk. It can be given by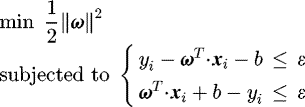 (4)
(4)
when the ε is given, the equation (4) can be solved by any proper algorithm. In order to solve practical problems, we had extended the above mathematical model, and the detailed derivation process can be seen as the Appendix A and B.
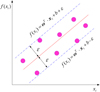 |
Fig. 1 SVR model. |
3 Fuzzy uncertainty model
The wear is a gradual process, and it is related to operational performance of equipments. The service conditions and material parameters can affect on the wear rate, which lead to different wear capacity in the same time period. In other words, there is uncertain of the wear under the same conditions, and it has a negative effect on the wear capacity. However, it is unrealistic to describe this uncertainty quantitatively. In order to decrease the effect of sample data which is outside the permissive range, the membership function is designed to express fuzzy uncertainty factors (load, speed, lubrication state).
The cylinder liner wear process experienced different wear levels (the initial wear, stable wear, severe wear). When the wear is close to maximum wear stipulated in the technical documents, the wear shows the fuzzy uncertainty characteristics. To model this phenomenon, two hypotheses are given: (1) when the wear is at the primary and stationary stages, the wear capacity can't exceed permissive range, (2) when the wear is at the severe stage, the wear capacity may exceed permissive range. The purpose of the hypotheses is to eliminate the inaccurate prediction caused by the sudden changes of working conditions, that is, to define the applicable scope of the model. Based on the hypotheses, the fuzzy function is employed to describe the uncertainty of the wear capacity in wear process. If the sample data exceed the given threshold, the membership function needs to play a role to make it within the specified range (see in Fig. 2), and the membership function of fuzzy function can be expressed as: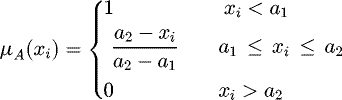 (5)where a1 and a2 are the wear capacity of the cylinder liner. We defined that the system is safe when the wear capacity within 95% of the maximum wear, and the system has a potential risk when the wear capacity is between 95% and 110% of the maximum wear. The wear capacity is monotonic increase, when the maximum wear capacity is given, a2 and a1 are determined. Based on this, a2 minus a1 is always positive, and the convexity of µA (xi) does not changed. The system is failure when the wear capacity exceeds the specified range.
(5)where a1 and a2 are the wear capacity of the cylinder liner. We defined that the system is safe when the wear capacity within 95% of the maximum wear, and the system has a potential risk when the wear capacity is between 95% and 110% of the maximum wear. The wear capacity is monotonic increase, when the maximum wear capacity is given, a2 and a1 are determined. Based on this, a2 minus a1 is always positive, and the convexity of µA (xi) does not changed. The system is failure when the wear capacity exceeds the specified range.
When considering the uncertainty factors, the membership function is introduced into the proposed SVR model, and a novel SVR model is established by combining SVR and membership function model. It can be given as (6)
(6)
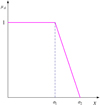 |
Fig. 2 Schematic diagram of membership function. |
4 Numerical application
The cylinder liner wear has a large impact on performance of the piston ring-cylinder system, and the wear can lead to the failure of the system. Therefore, the wear capacity of the cylinder liner is an important parameter for the ICEs. The top dead center of the cylinder liner is the worst working region due to the factors of the soot particles, wear particles, thermal loads and insufficient lubrication, and the maximum wear capacity always occurs in this region. Therefore, in order to prevent sudden failure, the wear capacity in the top dead center of cylinder liner is monitored to diagnose the operational state of the ICEs. In literature [16], the wear data of cylinder liner were reported, and cylinder liners were equipped a fleet of three identical cargo ships of the Grimaldi Group under similar loads, environment and operating conditions. The data set were collected from January 1999 to August 2006, the measure accuracy is 0.05 mm, and wear data were accumulated with the operational time of cylinder liners, as shown in Figure 3.
 |
Fig. 3 Wear data of the 32 cylinder liners. |
5 Result and discussion
5.1 Wear data analysis
In order to simulate the wear process and predict the trace of cylinder liner wear, the wear data are analyzed firstly. It can be seen from Figure 3 that the wear capacity increases non-linearly with operational time, and the linear methods cannot achieve the assessment of cylinder liner wear. Polynomial fitting can deal with non-linear problems, we try to use polynomial fitting method to process the collected data. The wear data are sorted from small to large according to the time sequence, and the relationship between cylinder liner wear and operational time are fitted by polynomial function, the results are shown in Figure 4. The result in Figure 4a shows that polynomial function can fit the average wear path, it cannot accurately assess the wear capacity in the next sample point. The residual analysis in Figure 4b also shows that polynomial regression method is not suitable for evaluating of cylinder liner wear. (The closer the residual is to 0, the better the results.) The polynomial regression function of Figure 4 can be expressed by equation (7). We can see that the equation (7) cannot satisfy the constraint of being null at ti = 0, and the regression function is only to find the average wear path from all the wear data. If it satisfies the constraint of being null at ti = 0, the fitting error will be greater. Through analyzing of the Figure 4, the different wear capacities indicate that there is uncertainty in system wear. Therefore, to realize the evaluation of cylinder liner wear, we need to find a more effective regression method to analyze the sample data.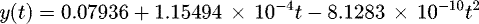 (7)
(7)
 |
Fig. 4 The polynomial fitting curve of the cylinder liner wear. (a) Polynomial fitting. (b) The residual analysis. |
5.2 The novel SVR for PSO
Based on the above analysis, the traditional regression methods are difficult to achieve the evaluation of cylinder liner wear process. Therefore, the new SVR model is used for analyzing the proposed problem. Due to the high no-linear, the kernel techniques are used to deal with nonlinear SVR. The Gaussian radial basis kernel function (GRBKF) is selected in this paper because the strong performance in handling nonlinear problems. In the new SVR model, the model parameters are vital important for the model, and they determine on the performance of the SVR. However, there is no effective way to determine the parameters value, so the optimization method is introduced into SVR model. The PSO algorithm is inspired from the rules by bird swarm activity [36,37]. It is an evolutionary computing technology which is established by using swarm intelligence, and it mainly uses the individual information sharing of the swarm to optimize the problem. In order to obtain the better consequence, the PSO algorithm is used for optimizing the model parameters. The mean square error (MSE) and squared correlation coefficient (R2) are used to judge the evaluation results, and it can be given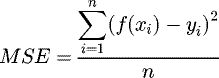 (8)
(8)
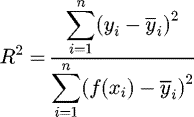 (9)
(9)
The wear data in literature [16] is used to assess the model parameters. The material properties and structure of the cylinder liners are the same, and thus the influence of different cylinder liners on wear is ignored. Generally, the number of samples in the training set should be sufficient, and the number of training samples is at least greater than 50% of the total number. Therefore, the 70% of the sample data are selected for model training, and the remaining parts are used to test model in this paper. Figure 5 shows the training results of cylinder liner wear by novel SVR. Figure 5a shows the comparison between the measured and the training value of cylinder liner wear on the training set. To observe the errors of proposed model, the 90% prediction interval is given in the figure. It can be seen from the figure that the errors are very small, and the training model can reflect the wear of cylinder liner. In order to understand the error between training and measured data more clearly, the comparison between measured and training data are shown in Figure 5b. We can draw the conclusion from Figure 5 that the training model is reliable. To illustrate the availability of the training model, the MSE and R2 are calculated, the results are shown in Table 1. In order to discuss the influence of the parameters on the solution, we changed the particle speed to improve the particle global search ability. The optimal results at different speeds are listed in Table 2. Compared with other results the existing results are optimal.
Figure 6 shows the testing results of cylinder wear using the training model. In Figure 6a, the measured data almost coincide with the testing value, and the variation trend of wear capacity indicates that the predicted data are reliable. It can be seen that the error is small, which further illustrates the availability of the proposed model. The comparison between measured data and testing data on testing set are characterized in Figure 6b, the small offset distance reveals that the training model is accurate for evaluating cylinder liner wear. In the testing set, the MSE and R2 are 0.010 and 0.968 respectively, which can illustrate the effectiveness of the model parameters.
Through the analysis of the cylinder liner wear data, the proposed SVR model can evaluate cylinder liner wear capacity of the ICEs. Whether in the training or testing set, the results are slightly different from the real values; it can reflect the basic conditions of cylinder liner wear. Comparing the proposed method with polynomial regression, obviously, the proposed model can describe the wear capacity of cylinder liner more accurately at different times.
 |
Fig. 5 The SVR training results of cylinder liner wear. (a) Comparison of training and measured data on the training set. (b) Performance of SVR on the training set. |
The MSE and R2 values of the SVR model on training set.
The MSE and R2 on training set at different speed rate.
 |
Fig. 6 The SVR testing results of cylinder liner wear. (a) Comparison of testing and measured data on the testing set. (b) Performance of SVR on the testing set. |
5.3 BPNN analysis
BPNN is a classic prediction algorithm, generally speaking, the consequences obtained by BPNN are reliable. To further verify the validity of the proposed model, the back propagation neural network algorithm is used to predict cylinder liner wear. In order to compare with proposed model, the sample data on training and testing set is set the same as the SVR model. The training network is obtained by processing the training data using BPNN. Based on the established training network, the predicted calculation is employed depend on the testing data. Figure 7 shows the BPNN testing results of the cylinder liner wear. In Figure 7a, we can see that the testing and measured data have the same varies trend, however, the error is relatively larger than SVR model. The performance of BPNN on the testing set is given in Figure 7b. The relative distances of measured data are obviously larger than testing data in the figure, which indicates the error is relatively large. Figure 8 is a comparison of the testing results between SVR and BPNN on the testing set. It can be seen from Figure 8 that the prediction data obtained from the SVR model are better than BPNN. Table 3 lists the MSE and R2 values of SVR and BPNN models on testing set. After comprehensive analysis, it is found that the SVR has a better performance on the prediction of cylinder liner wear.
 |
Fig. 7 The BPNN testing results of the cylinder liner wear. (a) Comparison of testing and measured data on the testing set. (b) Performance of BPNN on the testing set. |
 |
Fig. 8 Comparing of SVR and BPNN on the testing results. |
The MSE and R2 values of the SVR and BPNN model on testing set.
6 Conclusion
A novel wear assessment model is established based on the SVR in this paper. In order to evaluate the influence of the uncertainty, the external factors can be considered into the proposed model under small sample conditions. The experiment data of cylinder liner wear are employed to evaluate the effectiveness of the proposed model. The particle swarm optimization (PSO) algorithm is used to optimize the parameters of the proposed model. To verify superiority of the proposed model, a comparison with the BPNN is employment. The results show that the novel SVR has a better evaluating performance of mean square error and squared correlation coefficient, and higher regression performance under fuzzy uncertainty conditions, it can assess the cylinder liner wear of the internal combustion engines effectively.
Acknowledgments
This work was supported by the National Natural Science Foundation of China (Grant No. 51775428), the Key Research and Development Program of Shaanxi Province of China (Grant No. 2020GY-106) and the Open Project of State Key Laboratory for Manufacturing Systems Engineering (Grant No. sklms2020010).
Appendix A Model extension
In this paper, the equation (4) gives the mathematical model of SVR, however, not all the sample points are within the ±ϵ range. If the sample points are beyond the ±ϵ range, the relaxation factor ξi and ξi* (ξi, ξi* ≥ 0) must be introduced to satisfy the equation (3). Therefore, the equation (3) can be written as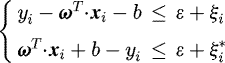 (A.1)
(A.1)
Thus, the minimizing problem of equation (4) can be written as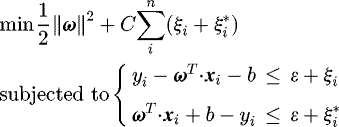 (A.2)where C is the penalty factor (C > 0), the purpose of the penalty factor is to control the penalty degree of the sample points. When consider the relaxation factor, the sample points outside the ±ϵ are called the ε −insensitive loss function (see in Fig. A.1). It can be expressed as [38]
(A.2)where C is the penalty factor (C > 0), the purpose of the penalty factor is to control the penalty degree of the sample points. When consider the relaxation factor, the sample points outside the ±ϵ are called the ε −insensitive loss function (see in Fig. A.1). It can be expressed as [38]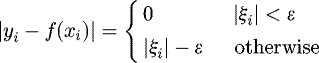 (A.3)
(A.3)
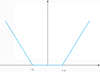 |
Fig. A.1 The ε-insensitive loss function. |
The equation (A.2) is the convex optimization problem, the Lagrange multipliers are introduced to solve the equation. Thus, the Lagrange function can be described as follows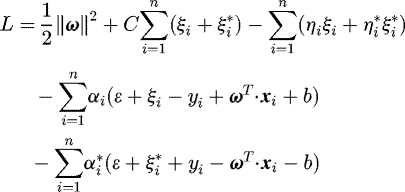 (A.4)where ηi, ηi*, αi, and αi* are the Lagrangian multipliers, and the ηi ≥ 0, ηi* ≥ 0, αi ≥ 0, and αi* ≥ 0.
(A.4)where ηi, ηi*, αi, and αi* are the Lagrangian multipliers, and the ηi ≥ 0, ηi* ≥ 0, αi ≥ 0, and αi* ≥ 0.
In order to obtain the optimal consequences of the proposing problem, the partial derivatives of the Lagrange function to the primal variables (ω,b,ξi,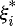 ) must be zero. It can be achieved by
) must be zero. It can be achieved by (A.5)
(A.5)
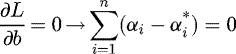 (A.6)
(A.6)
 (A.7)
(A.7)
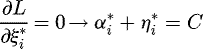 (A.8)
(A.8)
In finally, the line regression function can be written as
When the sample points present non-linear characteristics, the regression function can be written as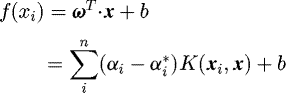 (A.10)where the K(xi,x) is the kernel function.
(A.10)where the K(xi,x) is the kernel function.
Appendix B Kernel function for SVR
In fact, in the SVR model, the most regression problems are no-linear rather than simple linear regression. In these cases, the computing method is required to map the sample data into high dimensional feature space. After introducing such a mapping, it is not necessary to solve the real mapping function, but only the kernel function needs to be known. In this way, only a specific kernel function needs to be given, which reduces the difficulty of solving regression equation greatly. The commonly used kernel functions are mainly classified into the following categories:
(2) Polynomial Kernel Function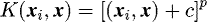 (B.2)where c ≥ 0, if c > 0, K is the nonhomogeneous polynomial kernel function. If c = 0, K is the homogeneous polynomial kernel function. P is the arbitrary positive integer, which can control the number of the vapnik-chervonenkis (VC) dimensions.
(B.2)where c ≥ 0, if c > 0, K is the nonhomogeneous polynomial kernel function. If c = 0, K is the homogeneous polynomial kernel function. P is the arbitrary positive integer, which can control the number of the vapnik-chervonenkis (VC) dimensions.
(3) Gauss Radial Basis Kernel Function (GRBKF)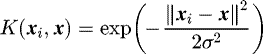 (B.3)
(B.3)
Gauss radial basis kernel function has a high flexibility, and its flexibility can be controlled by σ. where σ is the variance.
(4) Sigmoid Kernel Function (B.4)
(B.4)
In general, the different kernel functions will produce different consequences. Therefore, choosing the appropriate kernel function is of vitally important.
References
- D.E. Richardson, A literature review of the effects of piston and ring friction and lubricating oil viscosity on fuel economy, SAE Trans. 87, 2619–2638 (1978) [Google Scholar]
- J. Biberger, H.J. Fußer, Development of a test method for a realistic, single parameter-dependent analysis of piston ring versus cylinder liner contacts with a rotational tribometer, Tribol. Int. 113, 111–124 (2017) [Google Scholar]
- E. Tomanik, El.M. Mansori, R. Souza et al., Effect of waviness and roughness on cylinder liner friction, Tribol. Int. 120, 547–555 (2018) [Google Scholar]
- M. Yousfi, S. Mezghani, I. Demirci et al., Smoothness and plateauness contributions to the running-in friction and wear of stratified helical slide and plateau honed cylinder liners, Wear 332, 1238–1247 (2015) [Google Scholar]
- M. Soderfjall, A. Almqvist, R. Larsson, Component test for simulation of piston ring-Cylinder liner friction at realistic speeds, Tribol. Int. 104, 57–63 (2016) [Google Scholar]
- Y.Z. Zhang, A. Kovalev, N. Hayashi et al., Numerical prediction of surface wear and roughness parameters during running-in for line contacts under mixed lubrication, J. Tribol. 140, 061501 (2018) [Google Scholar]
- B. Zabala, A. Igartua, X. Fernandez et al., Friction and wear of a piston ring/cylinder liner at the top dead centre: experimental study and modelling, Tribol. Int. 106, 23–33 (2017) [Google Scholar]
- Y. Hamid, A. Usman, S.K. Afaq et al., Numeric based low viscosity adiabatic thermo-tribological performance analysis of piston-skirt liner system lubrication at high engine speed, Tribol. Int. 126, 166–176 (2018) [Google Scholar]
- C. Liu, Y.J. Lu, Y.F. Zhang et al., Numerical study on the tribological performance of ring/liner system with consideration of oil transport, ASME J. Tribol. 141, 011701 (2019) [Google Scholar]
- C. Liu, Y.J. Lu, Y.F. Zhang et al., Investigation on the frictional performance of surface textured ring-deformed liner conjunction in internal combustion engines, Energies 12, 2761 (2019) [Google Scholar]
- B. Fan, S. Feng, Y.T. Che et al., An oil monitoring method of wear evaluation for engine hot tests, Int. J. Adv. Manufactur. Technol. 94, 3199–3207 (2018) [Google Scholar]
- O. Altıntas, M. Aksoy, E. Unal et al., Artificial neural network approach for locomotive maintenance by monitoring dielectric properties of engine lubricant, Measurement 145, 678–686 (2019) [Google Scholar]
- H. Raposo, J.T. Farinha, I. Fonseca et al., Predicting condition based on oil analysis a case study, Tribol. Int. 135, 65–74 (2019) [Google Scholar]
- W. Cao, H. Zhang, N. Wang et al., The gearbox wears state monitoring and evaluation based on on-line wear debris features, Wear 426, 1719–1728 (2019) [Google Scholar]
- M. Giorgio, M. Guida, G. Pulcini, A wear model for assessing the reliability of cylinder liners in marine diesel engines, IEEE Trans. Reliab. 56, 158–166 (2007) [Google Scholar]
- M. Giorgio, M. Guida, G. Pulcini, A state-dependent wear model with an application to marine engine cylinder liners, Technometrics 52, 172–187 (2010) [Google Scholar]
- M. Giorgio, M. Guida, G. Pulcini, The transformed gamma process for degradation phenomena in presence of unexplained forms of unit-to-unit variability, Qual. Reliab. Eng. Int. 34, 1–20 (2018) [Google Scholar]
- M. Giorgio, G. Pulcini, A new state-dependent degradation process and related model misidentification problems, Eur. J. Oper. Res. 267, 1027–1038 (2018) [Google Scholar]
- M. Giorgio, M. Guida, F. Postiglione et al., Bayesian estimation and prediction for the transformed gamma degradation process, Qual. Reliab. Eng. Int. 34, 543–562 (2018) [Google Scholar]
- Y.F. Li, H.Z. Huang, H.L. Zhang et al., Fuzzy sets method of reliability prediction and its application to a turbocharger of diesel engines, Adv. Mech. Eng. 2013, 216192 (2013) [Google Scholar]
- M.S. Chang, J.H. Shin, Y.I. Kwon et al., Reliability estimation of pneumatic cylinders using performance degradation data, Int. J. Precis. Eng. Manufactur. 14, 2081–2086 (2013) [Google Scholar]
- S. Hermann, F. Ruggeri, Modeling wear in cylinder liners, Qual. Reliab. Eng. Int. 33, 839–851 (2017) [Google Scholar]
- Z.X. Zhang, C.H. Hu, X. He et al., Lifetime prognostics for deteriorating systems with time-varying random jumps, Reliab. Eng. Syst. Saf. 167, 338–350 (2017) [Google Scholar]
- P. Wiederkehr, T. Siebrecht, N. Potthoff, Stochastic modeling of grain wear in geometric physically-based grinding simulations, CIRP Ann. 67, 3253–3258 (2018) [Google Scholar]
- X.J. Xu, Z.Z. Zhao, X.B. Xu et al., Machine learning-based wear fault diagnosis for marine diesel engine by fusing multiple data-driven models, Knowl. Based Syst. 190, 105324 (2020) [Google Scholar]
- A. Panda, A.K. Sahoo, I. Panigrahi et al., Prediction models for on-line cutting tool and machined surface condition monitoring during hard turning considering vibration signal, Mech. Ind. 21, 520 (2020) [Google Scholar]
- I. Lazakis, Y. Raptodimos, T. Varelas, Predicting ship machinery system condition through analytical reliability tools and artificial neural networks, Ocean Eng. 152, 404–415 (2018) [Google Scholar]
- D.D. Kong, Y.J. Chen, N. Li, Hidden semi-Markov model-based method for tool wear estimation in milling process, Int. J. Adv. Manufactur. Technol. 92, 3647–3657 (2017) [Google Scholar]
- D.D. Kong, Y.J. Chen, N. Li, Gaussian process regression for tool wear prediction, Mech. Syst. Signal Process. 104, 556–574 (2018) [Google Scholar]
- D.D. Kong, Y.J. Chen, N. Li et al., Relevance vector machine for tool wear prediction, Mech. Syst. Signal Process. 127, 573–594 (2019) [Google Scholar]
- S. Dutta, S.K. Pal, R. Sen, On-machine tool prediction of flank wear from machined surface images using texture analyses and support vector regression, Precis. Eng. 43, 34–42 (2016) [Google Scholar]
- G.P. Zhang, J. Wang, S.P. Chang, Predicting running-in wear volume with a SVMR-based model under a small amount of training samples, Tribol. Int. 128, 349–355 (2018) [Google Scholar]
- I.I. Argatova, Y.S. Chai, An artificial neural network supported regression model for wear rate, Tribol. Int. 138, 211–214 (2019) [Google Scholar]
- Y.F. Yang, Y.L. Guo, Z.P. Huang et al., Research on the milling tool wear and life prediction by establishing an integrated predictive model, Measurement 145, 178–189 (2019) [Google Scholar]
- G.P. Zhang, X.J. Liu, W.L. Lu, A parameter prediction model of running-in based on surface topography, J. Eng. Tribol. 227, 1047–1055 (2013) [Google Scholar]
- J. Kennedy, R. Eberhart, Particle swarm optimization, in 1995 IEEE International Conference on Neural Networks, Perth, 1995, pp. 1942–1948 [Google Scholar]
- R. Eberhart, J. Kennedy, A new optimizer using particle swarm theory, in Sixth International Symposium on Micro Machine and Human Science, Nagoya, 1995, 39–43 [Google Scholar]
- X.S. Yang, Introduction to algorithms for data mining and machine learning, Academic Press, 2019, pp. 129–138 [Google Scholar]
Cite this article as: J. Kang, Y. Lu, H. Luo, J. Li, Y. Hou, Y. Zhang, Wear assessment model for cylinder liner of internal combustion engine under fuzzy uncertainty, Mechanics & Industry 22, 29 (2021)
All Tables
All Figures
 |
Fig. 1 SVR model. |
| In the text | |
 |
Fig. 2 Schematic diagram of membership function. |
| In the text | |
 |
Fig. 3 Wear data of the 32 cylinder liners. |
| In the text | |
 |
Fig. 4 The polynomial fitting curve of the cylinder liner wear. (a) Polynomial fitting. (b) The residual analysis. |
| In the text | |
 |
Fig. 5 The SVR training results of cylinder liner wear. (a) Comparison of training and measured data on the training set. (b) Performance of SVR on the training set. |
| In the text | |
 |
Fig. 6 The SVR testing results of cylinder liner wear. (a) Comparison of testing and measured data on the testing set. (b) Performance of SVR on the testing set. |
| In the text | |
 |
Fig. 7 The BPNN testing results of the cylinder liner wear. (a) Comparison of testing and measured data on the testing set. (b) Performance of BPNN on the testing set. |
| In the text | |
 |
Fig. 8 Comparing of SVR and BPNN on the testing results. |
| In the text | |
 |
Fig. A.1 The ε-insensitive loss function. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.