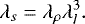| Issue |
Mechanics & Industry
Volume 23, 2022
|
|
|---|---|---|
| Article Number | 2 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.1051/meca/2021051 | |
| Published online | 21 January 2022 | |
Regular Article
Aeroelastic scaling of flying demonstrators: mode tracking technique
1
Institut Clément Ader, Université de Toulouse, ISAE-SUPAERO-CNRS-INSA-Mines Albi-UPS,
Toulouse, France
2
ONERA/DTIS, Université de Toulouse,
Toulouse, France
* e-mail: joan.mas.colomer.academic@gmail.com
Received:
15
March
2021
Accepted:
11
December
2021
Aeroelastic scaling theory shows that the design problem of aeroelastically equivalent scaled aircraft can be treated as a structural-only design problem if the aerodynamic shape and airflow properties of the full scale aircraft are preserved. In that case, the theory shows that it is sufficient to match the scaled natural mode shapes, frequencies and mass of the reference aircraft. In this paper, we present a new method for the dynamic scaling of flexible structures where the objective function is based on the modal assurance criterion (MAC). This criterion is used for a mode tracking strategy during the optimization process. Finally, we apply this method to a scaled version (1:5) of the uCRM wing, achieving an agreement greater than 99% on the average MAC value of the first 5 modes.
Key words: Aeroelastic scaling / modal matching / modal assurance criterion / optimization
© J. Mas Colomer et al., Published by EDP Sciences 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Traditionally, aeroelastically scaled models have been used as a fast and reliable technique to determine the aeroelastic behavior of their full-size counterparts, especially in wind-tunnel testing. In a context where aircraft designers seek for more efficient designs, they are often lead to explore new types of aircraft. The use of scaled models to test the aeroelastic qualities presents itself as fast and economic means to validate the flying behavior of these innovative aircraft concepts. Thus, for the scaled results to be representative of the ones expected from the full-scale, a design process is required that ensures the same aeroelastic behavior. In this paper we present an automated method to establish the structural sizing of a scaled model that exhibits the same scaled structural dynamics behavior as the full size aircraft of interest. The underlying idea is to be able to use such scaled models to evaluate, in practice, new aircraft concepts or modifications to existing aircraft types (e.g., new engine that implies structural modifications and a new mass distribution).
Bisplinghoff et al. [1] described the fundamentals of aeroelastic scaling in 1955. Later, Scruton and Lambourne [2] also included the effects of compressibility and heat transfer. To create wind tunnel models that are aeroelastically equivalent, French [3] used an optimization technique to establish the parameters of a finite element model so that the static response is matched. To include the dynamic scaling, French and Eastep [4] later presented a method with two optimization steps. The structural stiffness is first matched by minimizing the error in static deflections under a reference load. On the second step, the values of non-structural masses are determined using an optimization formulation that minimizes the error in modal shapes while setting the scaled natural frequencies as constraints.
About a decade later, Pereira et al. [5] used an optimization approach to match the scaled natural frequencies for the design of a joined-wing wind tunnel model. In addition to the natural frequencies, and considering the same application case of the joined-wing aircraft, Bond et al. [6] proved that matching the mode shapes was required as well. Richards et al. [7] established a comparison between a single-step optimization for modal matching, which includes both stiffness and mass characteristics as design variables, and the decoupled approach described above.
Ricciardi et al. [8] introduced a modification in the two-step approach used by Richards et al. [7] to also match the static deflections obtained by nonlinear analysis in the stiffness optimization loop. These last two works are intended to establish the design of a flying scaled version of the joined-wing SensorCraft model. In further studies, Ricciardi et al. [9] considered a single-step approach in which the displacements obtained both by linear and nonlinear static analysis are matched, while ensuring—through optimization constraints—that the equality of the scaled natural frequencies is satisfied. More recently, Ricciardi et al. [10] described an optimization-based method to match both the vibration modes and eigenvalues, in addition to the linear static response. They also mention the phenomenon of mode swapping and mixing throughout the optimization process. Recently, Mas Colomer et al. [11] introduced the aeroelastic scaling of the static response in the situations where flow similarity cannot be achieved. In the context of the classical aeroelastic scaling (i.e., assuming flow similarity exists), they proposed and evaluated the use of a mode tracking strategy to address the problem of mode crossing. The works by Spada et al. [12] constitute an example of the recent developments of the two-step method for modal optimization applied to high aspect ratio wings.
In this paper we present and describe the optimization problem that we propose to solve the modal similarity. We highlight the new aspects that we introduce with respect to the traditional method described by Ricciardi et al. [9], such as the use of the modal assurance criterion (MAC) in the definition of the objective function and the introduction of a mode tracking strategy to avoid potential problems during the optimization process. Next, to evaluate the method, we apply it to obtain the scaled structural sizing of a scaled (1:5) version of the uCRM wing1 [13].
2 Theoretical background
As described by Ricciardi et al. [9], where the traditional scaling theory is described, under certain assumptions, the complete static and dynamic aeroelastic similarity can be reduced to obtaining a structure whose nondimensional natural vibration modes, frequencies and mass match those of the reference aircraft. This approach is similar to the finite element model updating [14,15] to match experimental data. However, in the present case the finite element is the one corresponding to the reduced scale and the target modal quantities are not obtained experimentally but given by scaling the theoretical ones of the reference aircraft. As described by Bisplinghoff [1] and Ricciardi et al. [9], these assumptions include the preservation of the flow similarity and the external aerodynamic shape. The flow similarity requirement translates into keeping the same Mach number for compressibility effects, the Reynolds number for viscous effects, and the Froude number for gravitational effects. The same external aerodynamic shape condition is achieved by ensuring that the outer mold line (OML)—the manufacturing shape of the model aircraft’s outer surface—is a scaled version of the reference aircraft one. In the context of this paper, we make the hypothesis, assumed by the classical aeroelastic scaling theory [1], that complete aerodynamic similarity in terms of both the airflow properties and the OML exists.
The general form of the nondimensional equation of aeroelasticity is
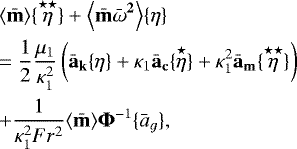 (1)
(1)
where 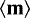 is the diagonal matrix of modal masses,
is the diagonal matrix of modal masses,  is the diagonal matrix of modal frequencies, {η} is the vector of modal coordinates, μ1 is the inertia ratio, κ1 is the reduced frequency (using the frequency of the first reference mode for nondimensionalization), [a] are the aerodynamic matrices, Fr is the Froude number, [Φ] is the matrix of normal modes, ★ indicates the differentiation with respect to nondimensional time, and an overbar (−) indicates a nondimensional quantity. For more details on the derivation of equation (1) and the hypotheses used (e.g., neglected structural damping) refer to the works by Ricciardi et al. [9] and Mas Colomer [16]. By looking at equation (1), we see how satisfying all the conditions on the flow similarity, preserving the scaled aerodynamic shape (nondimensional aerodynamic matrices depend on scaled OML and flow properties only), and ensuring the equality of the nondimensional coefficients, as well as the nondimensional modal masses and normal modes, guarantees the identity of the right-hand side of the equations of two aircraft of different scales. We then see that the left-hand side involves terms that are related to the structural analysis uniquely. Therefore, the aeroelastic scaling process reduces to matching the scaled natural mode shapes, frequencies, and modal effective masses.
is the diagonal matrix of modal frequencies, {η} is the vector of modal coordinates, μ1 is the inertia ratio, κ1 is the reduced frequency (using the frequency of the first reference mode for nondimensionalization), [a] are the aerodynamic matrices, Fr is the Froude number, [Φ] is the matrix of normal modes, ★ indicates the differentiation with respect to nondimensional time, and an overbar (−) indicates a nondimensional quantity. For more details on the derivation of equation (1) and the hypotheses used (e.g., neglected structural damping) refer to the works by Ricciardi et al. [9] and Mas Colomer [16]. By looking at equation (1), we see how satisfying all the conditions on the flow similarity, preserving the scaled aerodynamic shape (nondimensional aerodynamic matrices depend on scaled OML and flow properties only), and ensuring the equality of the nondimensional coefficients, as well as the nondimensional modal masses and normal modes, guarantees the identity of the right-hand side of the equations of two aircraft of different scales. We then see that the left-hand side involves terms that are related to the structural analysis uniquely. Therefore, the aeroelastic scaling process reduces to matching the scaled natural mode shapes, frequencies, and modal effective masses.
In general, according to the traditional scaling theory [4], these modal responses are matched through an optimization problem where the parameters defining the structural model (e.g., plate thicknesses, beam sections, and point masses) are set as design variables and the idea of matching the scaled frequencies, shapes, and mass is implemented through equality constraints and by minimizing a certain function quantifying the error on the modal responses. On the literature [9,17] we find different examples of the definition of this modal matching problem. The modal responses are always matched for a limited number of modes denoted by N.
For example, Ricciardi et al. [9] describe a formulation for this problem where the objective function to be minimized is
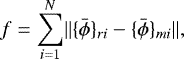 (2)
(2)
where 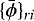 and
and 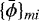 are the N nondimensional modes of the reference aircraft and the scaled model, respectively. For the nondimensional matching, they set N equality constraints
are the N nondimensional modes of the reference aircraft and the scaled model, respectively. For the nondimensional matching, they set N equality constraints
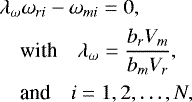 (3)
(3)
where ωri and ωmi are the N natural frequencies of the reference aircraft and the scaled model respectively, b is the reference length of each scale, and V is the airspeed of each scale.
Another example of the modal optimization setup is proposed by Pires [17]. In his work, Pires defines an unconstrained minimization problem where the objective function includes both the error in mode shapes and in frequencies.
In general, the structural design variables of this problem can be divided into variables affecting the stiffness and mass properties simultaneously (such as plate thicknesses and beam sections), and variables affecting the mass distribution only (e.g., point masses). One possible approach, as described by Richards et al. [7], is to treat this optimization problem by using a single-step approach where the structural element properties (e.g., thicknesses, sections) and mass-specific variables are optimized at once on a single optimization loop. Richards et al. [7] also describe an alternative approach that aims to reduce the complexity of the original problem. This second approach consists in first matching the scaled stiffness of the reference aircraft by optimizing only the variables that affect stiffness (e.g., thicknesses and section) and then perform the modal matching (i.e., shapes and frequencies) through optimization of the mass-specific variables.
3 Definition of the optimization problem for modal similarity
We will now present and discuss the choices adopted for the modal matching criteria (i.e., what quantities we set as the objective function and constraints), as well as the choices regarding the single-step approach for the optimization. Concerning the formulation of the optimization problem we choose to use the MAC value to represent the closeness between two vibration modes. The methodology that we present is close to the one described by Prananta et al. [18] and Gupta et al. [19], which they used to update finite element models to match experimental data. As described by Allemang [20], if {ϕri } is one of the reference eigenvectors, and {ϕmj} is one of theeigenvectors from the current model, we define a matrix whose elements are
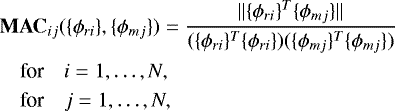 (4)
(4)
which is the normalized dot product between two vectors {ϕri} and {ϕmj} representingtwo modes. Indeed, a MAC value of 1 indicates that the two vectors represent the same mode, whereas a MAC value of 0 indicates that the two modes are orthogonal. Given a set of N reference modes and N modes that we want to evaluate, we define this N × N matrix—equation (4)—containing the MAC value for each possible pair of modes between the reference ones and the ones being analyzed. Given the matrix [MAC] we define the objective function to be minimized as
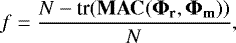 (5)
(5)
where tr() indicates the trace of a matrix, [Φr] is the matrix containing the reference modes and [Φm] contains the modes being analyzed. This objective function is equivalent to the one proposed by Giraldo [21], used in the field of health monitoring of civil structures. It is also similar to the one proposed by Morlier et al. [22]. For the scaled frequency matching, we set an equality constraint for each scaled frequency, as used by Ricciardi et al. [9] and defined in equation (3). Also, we set an equality constraint for the scaled mass
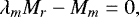 (6)
(6)
where λm is the mass ratio, Mr is the mass of the reference aircraft, and Mm is the mass of the scaled model (a function of the design variables). By doing so, we aim to avoid having a multiplicity of solutions that closely match the reference modal shapes and frequencies. By using the mass constraint we choose the solution that matches the scaled mass, in addition to mode shapes and frequencies.
Regarding the strategy for the solution of the optimization problem, we choose to adopt a single-step approach, where all the structural design variables are optimized at the same time. One reason to choose this approach over a two-step approach, where a stiffness matching is performed before the modal optimization loop, is that the latter could potentially lead to a suboptimal solution of the modal matching problem. To explain this, we consider a vector of design variables {s} that affect the stiffness (and that may or may not contribute to the mass of the structure). Also, we consider the design variables {m} that affect the mass only. Then, we denote as {s*} and {m*} the particular values of these vectors that are the solution to the modal matching problem. On the other hand, we denote as {s† } the vector of stiffness variables that satisfies the stiffness matching problem. Then, we denote as {m† } the mass-specific variables that satisfy the modal matching problem under the condition that {s} = {s†}. If the design space of the single-step approach—whose solution is ({s*}, {m*})—includes the design space of the two-step approach, the modal matching corresponding to ({s* }, {m*}) will, in the general case, be better than the one corresponding to ({s†}, {m†}), by definition of the optimum. It is to say, the solution of the one-step approach will, in general, be better than the one found with the two-step approach since the design space of the latter is conditioned to satisfy the stiffness matching problem.
4 Definition of a mode tracking strategy
In this section, we will propose a mode tracking strategy based on the MAC value, whose mathematical definition was presented on Section 3. In this work, we define a mode tracking strategy as a means of ordering the normal modes of a structure defined by a set of design variables {x} in a way that the evolution with respect to {x} of the shapes and frequencies of these modes is both continuous and smooth. The proposed mode tracking strategy presented in this section is inspired from the works by Kim and Kim [23] as well as the strategy proposed by Ting et al. [24].
The main idea of this mode tracking strategy is to order the modes of the design being analyzed in a way that, for each of the N reference modes, its associated mode is, among all the modes of the current design defined by {x}, the one that most closely resembles the reference one. As we use the MAC to define the resemblance between modes, each reference mode is associated to the mode of the current design whose MAC value with the given reference one is the highest (i.e., the closest to 1). Since the mode with the highest resemblance to a given reference mode could have a frequency that is not necessarily within the first N frequencies, this search should be extended to a sufficiently large number M of eigenvectors in order not to exclude the best matching mode. Therefore, the effectiveness of the described method is conditioned to whether the best matching modes are included in the first M modes specified for the analysis of the current design defined by {x}. Ideally, M would be arbitrarily large, in order to make sure that none of the best matching modes is left out. However, in practice, increasing M increases the computational cost of each modal analysis. Therefore, there is a compromise between M and the computational cost. In consequence, M should be chosen as big as possible while keeping the computational time within reasonable limits.
Given the set of N reference vectors, in order to find the N best matching modes among the M modes of the current model, we define a N × M rectangular matrix, based on the definition on equation (4), which evaluates the resemblance between the reference modes and the unsorted modes of analysis as
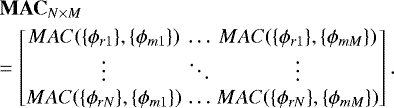 (7)
(7)
Then, for each row of the [MAC]N×M matrix (i.e., for each of the reference modes), the mode with the highest MAC value is paired with the current reference mode. Once the modes of the model being analyzed are paired to the reference ones, we can redefine the order of the modal frequencies ωmi and the modal vectors {ϕmi }. The order is such that the mode {ϕmi} is the one that most closely matches the mode {ϕri}. The order of the natural frequencies is modified accordingly, so that ωmi is the natural frequency associated to the mode {ϕmi}.
After having reordered the modal quantities according to the MAC, all the quantities of interest, namely the objective function on equation (5) and the frequencies on equation (3), can be evaluated. For the objective function, the square MAC matrix involved in its evaluation is now computed using the N modes that have been paired to the first N reference ones. In the case where the modes matched perfectly, the diagonal of the square MAC matrix used for the evaluation of f would be composed of ones. Consequently, with the objective function in equation (5), we search to maximize the overall resemblance of the modes, by maximizing the trace, which is the sum of the elements of the diagonal. Although in this paper we only consider the diagonal terms, we could also include the sum of the off-diagonal terms in the objective function to try to minimize them, since in the case of a perfect modal matching all the off-diagonal terms would be zero.
In the following sections, we will see two examples of the application of the modal optimization formulation described above.
5 Example of application to the scaled uCRM wing
In this section we will apply the modal optimization described at the beginning of this paper to a scaled version of the undeflected Common Research Model (uCRM) wing [13]. The uCRM wing is a modified version of the NASA Common Research Model Wing (CRM) [25]. Since the original CRM wing was intended for CFD studies, its shape corresponds to an inflight configuration and therefore includes elastic displacements. The uCRM was developed to obtain the undeflected geometry of a wing with structural characteristics of a typical airliner that, when subject to inflight loads, results in the shape of the orignal CRM wing. In this paper, we have chosen a scale of 1 : 5 (length ratio λl = 1∕5), since the initial estimations of the structural thickness—described next—suggest that using a smaller scale would lead to unfeasible gauge values of the aluminum plates constituting the structure. As explained by Pires [17], to determine the mass scaling ratio we first need to determine the air density ratio (λρ). For that purpose, we establish the air conditions of each scale using the international standard atmosphere.The full-scale uCRM wing is considered to fly at altitude conditions of a typical airliner (35, 000 ft), whereasthe scaled model is considered to fly at low altitude (2000 m ≃ 6562 ft). As explained by Pires [17], the natural frequency (λω) and mass (λm) ratios are
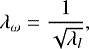 (8)
(8)
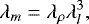 (9)
(9)
respectively.
Since for this problem we use the gradient-free optimizer COBYLA [26], which requires the user to provide a starting point, we will try to determine a starting design that is reasonably close to the optimum. For that purpose, we use the method proposed by Mas Colomer et al. [27], based on the Euler beam theory and the properties of thin-walled structures, to obtain a factor to scale down the thicknesses and stringer sections of the full-scale model to be used as the initial design for the optimization. Using this method, the scaling factors of the thicknesses and stringer sections can be estimated respectively as
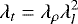 (10)
(10)
This simple method allows us to have a first estimation of the thickness and cross-sections of the elements constituting the scaled structure, to be used as the starting point for the optimizer. This estimation is simply obtained by multiplying the thickness and cross-sections of the full-scale model by λt and λs, respectively. For the initial value of the point masses, these will be estimated by using the mass ratio λm, defined on equation (9).
For this case, we first choose to match the first N = 5 modes of the reference wing, and we choose to extract M = 20 for the modal analysis of each optimization iteration. Later, we consider the same optimization problem with N = 10 and M = 30. Table 1 summarizes the current optimization problem.
The design variables that we have chosen for this problem are 12 shell thicknesses {t}, 6 stringer section values {s}, and 4 point mass values {m}, giving a total of 22 design variables. As illustrated in Figure 1, the upper and lower skins of the wing are divided into 6 different thickness regions along its longitudinal axis. Each of these regions defines a single thickness value of the upper and lower skin, as well as the ribs within this section. The front and aft spars are also divided into 6 other regions. Each one of these regions defines a single thickness value of the spar caps and web comprised within each section. Another set of 6 design variables defines 6 different stringer cross-section values. These regions of different stringer properties are depicted in Figure 2. There is a total of 20 point masses in the finite element of the wing structure, which are grouped in 4 different mass values, thus constituting the 4 mass design variables. As explained in Section 3, we perform a single-step approach where stiffness and mass related variables are optimized at once on a single optimization loop. For this problem we use the COBYLA [26] optimizer, which is a gradient-free, local optimizer. One of the reasons to use a gradient-free algorithm is that the open-source version of NASA’s Nastran2 [28] does not provide the derivatives of the modal quantities of interest with respect to the inputs. The derivatives could have been estimated using finite differences, although this presents two drawbacks in this case: the high number of evaluations required to estimate thegradients (22 design variables) and the fact that Nastran produces output text files with a limited number of digits for the responses, which could lead to cancellation errors in the computation of finite differences. In the two optimization cases presented in this paper, we set the maximum number of iterations to 500 and the absolute tolerance on the size of COBYLA’s trust region to 10−3. The optimizer will stop whenever one of the two criteria is met.
Modal optimization problem for structural dynamic scaling.
 |
Fig. 1 Different thickness regions for modal optimization (12 in total). For each section, the thickness of the panels on the lower surface of the wing is the same as on the upper side. |
 |
Fig. 2 Different stringer property regions for modal optimization (6 in total). |
6 Results and discussion
6.1 Case for N = 5
After running the previously described problem for the first N = 5 modes, we observe, in Figure 3, that the results in terms of the average MAC value (the trace of the MAC matrix divided by N) are satisfactory: the average MAC value is greater than 0.99 (since f < 0.01, recall the definition in Eq. (5)), allowing us to say that the modal matching of the first 5 modes has a good quality. We can see the improvement of the optimized design with respect to the initial design in Figure 4, especially for the shape of modes 4 and 5. We see that, after 500 iterations (the maximum number of iterations is reached), the frequency constraints as well as the mass constraint present a good convergence to the required value of 0. The mass constraint in Figure 3 has been normalized using the scaled reference mass λm Mr, whereas each one of the components of the frequency constraint has been normalized using its corresponding scaled reference frequency λω ωri. Note that for the first iterations, some of them present better objective function values than the converged one, but these points are not feasible since for these iterations the constraints are not respected. During the first iterations (around 80) COBYLA first performs an exploration of the design space before actually searching in the direction of the minimum.
By using the previously described mode tracking strategy we can check whether mode-crossing actually took place during the optimization process. To do so, we plot in Figure 5 the evolution (against the optimization iterations) of the frequency of the modes of the current model that are associated to the selected reference modes.
As we see on Figure 5, no mode crossing takes place during this optimization process, since the order of the natural frequencies according to their value remains the same as the order according to the reference shape they are associated to (i.e., lines corresponding to different shapes do not cross during the optimization history).
 |
Fig. 3 Evolution of the best found design with the number of iterations using COBYLA for N = 5. The objective function (a), the frequency constraints (b) (Eq. (3)), and the mass constraint (c) (Eq. (6)) are plotted as a function of the iterations. |
 |
Fig. 4 On the left, modal results of the first optimization iteration (initial guess, in red) overlapped with the reference ones (blue). On the right, optimized modes (green) overlapped with the reference ones for the case of N = 5. |
 |
Fig. 5 Evolution of the natural frequencies of the current model sorted according the best corresponding reference modes. The frequencies of the 4th and 5th modes nearly intersect around iteration 40, however their values do not cross during the optimization process. |
6.2 Case for N = 10
After running the previously described problem for the first N = 10 reference modes usingthe COBYLA optimizer, we can see the evolution of the quantities of interest with the number of iterations, as shown in Figure 6. The mass constraint in Figure 6 has been normalized using the scaled reference mass λmMr, whereas each one of the components of the frequency constraint has been normalized using its corresponding scaled reference frequency λω ωri. We see that, after 305 iterations (in that case, the tolerance on COBYLA’s trust region is reached before the maximum number of iterations), the frequency constraints converge to the required value of 0, with a maximum relative error of 0.83% for the scaled natural frequency of the 9th mode. The scaled total mass constraint converges with an error of − 1.83%. The minimum of the objective function—characterizing the mode shape similarity—that satisfies the constraints within the mentioned errors is fmin = 0.2, which implies that the average MAC value of the N = 10 modes considered for the comparison is 1 − fmin = 0.8 (recall the definition in Eq. (5)). Therefore, in this case the results are less satisfactory than for N = 5 in all three aspects: mode shapes, frequencies and mass. As in the previous case, some points at the beginning of the search present better objective values than the converged one, but these do not satisfy the mass and frequency constraints.
Figure 7 shows the comparison between the scaled reference mode shapes and the mode shapes of the starting point design, as well as the comparison of the reference modes and the ones of the best design found by COBYLA after 305 iterations. Note that, in both cases, several modes (such as 7 and 8) that are represented by vectors withan opposite sign but that represent the same physical mode are correctly paired. We also see that the 6th mode exhibits a worse correlation after optimization with respect to the starting the point. This is possible since the adopted objective function considers the correlation of the modes as a whole, so it is possible that the design that produces the best MAC in average presents a value that is worse than the initial one for a particular mode.
Again, using the MAC-based mode tracking strategy we can check for the presence or lack of mode-crossing during the optimization in Figure 8. As we see on Figure 8, no mode crossing takes place during this optimization process, since the order of the natural frequencies according to their value remains the same as the order according to the reference shape they are associated to (i.e., lines corresponding to different shapes do not cross during the optimization history).
For comparison, we show the vector of design variables of the optimized design for each one of the previous situations (N = 5 and N = 10). Tables 2, 3, and 4 show, respectively, the thickness, section and mass vectors for these two situations. This method can be applied to any number N of modes, but in aircraft design only the modes that are implied in the aeroelastic phenomena are usually considered (e.g., for the particular case of the uCRM wing considered here, the first 5 modes would be sufficient for the flutter analysis). For problems other than wing design, where this method can also be applied, if a large number of modes is considered (e.g., N >> 10), probably many more design variables would be required to capture all the local stiffness and mass properties that are involved in the higher order modes.
One of the main hypothesis of the classical aeroelastic scaling theory is that the flow properties and the external aerodynamic shape are completely scaled. In other works [29], we consider the case where the flow conditions cannot be completely matched and the implications that this has on the shape of the wing (and hence the shape of the structure) to ensure the same aeroelastic behavior.
 |
Fig. 6 Evolution of the best found design with the number of iterations using COBYLA for N = 10. The objective function (a), the frequency constraints (b) (Eq. (3)), and the mass constraint (c) (Eq. (6)) are plotted as a function of the iterations. |
 |
Fig. 7 Modal results of the first optimization iteration overlapped with the reference ones for N = 10. |
 |
Fig. 8 Evolution of the natural frequencies of the current model sorted according the best corresponding reference modes. |
Comparison of optimized thicknesses.
Comparison of optimized stringer sections.
Comparison of optimized point mass values.
7 Conclusion
We have seen that the classical scaling theory shows that in the case of airflow and aerodynamic shape similarity, the aeroelastic scaling problem is reduced to a design problem where the scaled modal shapes and frequencies have to be matched. We reviewed the traditional methods for modal optimization applied to aeroelastic similarity of flying scale demonstrators, seeing that objective functions based on the differences of coordinates of mode vectors can lead to discontinuities as they depend on how these vectors are normalized. Evaluating the mode shapes ordered according to eigenfrequencies can be another source of discontinuities in the objective function and on the derivatives of the frequencies if mode swapping exists. To avoid these potential drawbacks, we use an objective function based on the modal assurance criterion (MAC) to avoid the normalization problem. We also order the modes according to the MAC to avoid the negative effects of mode swapping.
We have tested this method for the first 5 modes of the uCRM wing, leading to an agreement greater than 99% in terms of theaverage MAC value of the considered modes, while satisfying the scaled eigenfrequencies and mass constraints.
As stated previously, for the case of N = 10, the average MAC value is 0.8. According to Girard and Roy [30], a MAC value of 0.9 is synonym of a good correlation, whereas a value smaller than 0.7 implies a rather poor correlation. After seeing these results, we conclude that is preferable to concentrate on well matching a more limited number of nodes (usually only the frequencies of the first modes are involved in the aeroelastic phenomena such as flutter), rather than attempting to match a relatively large number of modes (e.g., N = 10) and obtain a poorer result on average.
Since this method considers that the modes of the reference aircraft and the ones of the design being optimized are defined on the same node locations, a major improvement of the method to make it more general would be to use a mesh interpolation scheme so that the same mesh geometry is no longer a requirement. One possibility would be to use the technique proposed by Rendall and Allen [31]. In that case, one possibility would be to take the displacement vectors representing the reference modes and interpolate them on the structural grid of the model being optimized. In that manner, the reference modes and the modes of the current optimization iteration would be expressed in the same nodal locations and the MAC definition between vectors would remain the same as the one used throughout this paper. This would allow us to use the same optimization and mode tracking strategy with the only difference of the intermediate step of the reference mode interpolation in a common set of nodes. See [29] for an application of this method.
Also, an improvement is expected by considering not only the total scaled mass as a constraint, but also the scaled generalized modal masses, as they are more representative of how the mass is distributed across the structure. If that were the case, and given that the modal masses are computed both using the rotational and translation degrees of freedom, the output of the finite element solver would not be directly usable as a constraint. Indeed, the rotations do not depend on the scale, whereas the translation degrees of freedom depend on the length ratio between the models. Therefore, this would require some manipulation before the final output of the generalized modal masses of the scaled model given by the finite element solver.
Acknowledgements
This work is part of the activities of ONERA–ISAE–ENAC joint research group. The authors would like to thank Christophe Blondeau and Timothé Achard for their help and expertise on the CRM structural model.
References
- R.L. Bisplinghoff, H. Ashley, R.L. Halfman, Aeroelasticity, Courier Corporation (1996) [Google Scholar]
- C. Scruton, N. Lambourne, Similarity requirements for flutter model testing, in: E.C. Pike (Ed.), Manuel on Aeroelasticity, Vol. IV of AGARD, 1971, Chap. 6, pp. 1–26 [Google Scholar]
- M. French, An application of structural optimization in wind tunnel model design, in: 31st Structures, Structural Dynamics and Materials Conference, American Institute of Aeronautics and Astronautics, Long Beach, California (1990) [Google Scholar]
- M. French, F.E. Eastep, Aeroelastic model design using parameter identification, J. Aircraft 33, 198–202 (1996) [Google Scholar]
- P. Pereira, L. Almeida, A. Suleman, V. Bond, R. Canfield, M. Blair, Aeroelastic scaling and optimization of a joined-wing aircraft concept, in: 48th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, American Institute of Aeronautics and Astronautics, Honolulu, Hawaii, 2007 [Google Scholar]
- V.L. Bond, R.A. Canfield, A. Suleman, M. Blair, Aeroelastic scaling of a joined wing for nonlinear geometric stiffness, AIAA J. 50, 513–522 (2012) [Google Scholar]
- J. Richards, A. Suleman, R. Canfield, M. Blair, Design of a scaled RPV for investigation of gust response of joined-wing sensorcraft, in: 50th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, American Institute of Aeronautics and Astronautics, Palm Springs, California, 2009 [Google Scholar]
- A. Ricciardi, R. Canfield, M. Patil, N. Lindsley, Nonlinear aeroelastic scaling of a joined wing aircraft, in: 53rd AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics and Materials Conference, in American Institute of Aeronautics and Astronautics, Honolulu, Hawaii, 2012 [Google Scholar]
- A.P. Ricciardi, C.A.G. Eger, R.A. Canfield, M.J. Patil, Nonlinear aeroelastic-scaled-model optimization using equivalent static loads. J. Aircraft 51, 1842–1851 (2014) [Google Scholar]
- A.P. Ricciardi, R.A. Canfield, M.J. Patil, N. Lindsley, Nonlinear aeroelastic. J. Aircraft 53, 20–32 (2016) [CrossRef] [Google Scholar]
- J. Mas Colomer, N. Bartoli, T. Lefebvre, et al. Similarity maximization of a scaled aeroelastic flight demonstrator via multidisciplinary optimization, in: 58th AIAA/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference, American Institute of Aeronautics and Astronautics, Grapevine, Texas, 2017 [Google Scholar]
- C. Spada, F. Afonso, F. Lau, A. Suleman, Nonlinear aeroelastic scaling of high aspect-ratio wings. Aerospace Sci. Technol. 63, 363–371 (2017) [Google Scholar]
- T.R. Brooks, G.K.W. Kenway, J.R.R.A. Martins, Benchmark aerostructural models for the study of transonic aircraft wings. AIAA J. 56, 2840–2855 (2018) [CrossRef] [Google Scholar]
- M. Friswell, J.E. Mottershead, in: Finite element model updating in structural dynamics, Springer Science & Business Media (2013), Vol. 38 [Google Scholar]
- T. Marwala, Finite element model updating using computational intelligence techniques: applications to structural dynamics, Springer Science & Business Media (2010) [Google Scholar]
- J. Mas Colomer Aeroelastic similarity of a flight demonstrator via multidisciplinary optimization, Ph.D. thesis, Doctorat de l’Université de Toulouse délivré par: l’Institut Supérieur de l’Aéronautique et de l’Espace (ISAE), 2018 [Google Scholar]
- T. Pires, Linear Aeroelastic Scaling of a Joined Wing Aircraft, Instituto Superior Tecnico, TU Lisbon, 2014 [Google Scholar]
- B. Prananta, T. Kanakis, J. Vankan, R. van Houten, Model updating of finite element model using optimisation routine, Aircraft Eng. Aerospace Technol. 88, 665–675 (2016) [Google Scholar]
- A. Gupta, C.P. Moreno, H. Pfifer, B. Taylor, G.J. Balas, Updating a finite element based structural model of a small flexible aircraft, in: AIAA Modeling and Simulation Technologies Conference, 2015, p. 0903 [Google Scholar]
- R.J. Allemang, D.L. Brown, A correlation coefficient for modal vector analysis, in: Proceedings of the 1st international modal analysis conference, Vol. 1, SEM Orlando, 1982, pp. 110–116 [Google Scholar]
- D.F. Giraldo, A structural health monitoring framework for civil structures, Ph.D. thesis, Washington University, Saint Louis, Missouri, 2006 [Google Scholar]
- J. Morlier, A. Basile, A. Chiplunkar, M. Charlotte, An ego-like optimization framework for sensor placement optimization in modal analysis. Smart Mater. Struct. 27, 075004 (2018) [CrossRef] [Google Scholar]
- T.S. Kim, Y.Y. Kim, Mac-based mode-tracking in structural topology optimization. Comput. Struct. 74, 375–383 (2000) [CrossRef] [Google Scholar]
- T. Ting, T.L.C. Chen, W.J. Twomey, An automated mode tracking strategy (dynamic structural analysis of helicopterstructures), AIAA J. 33, 183–185 (1995) [CrossRef] [Google Scholar]
- J.C. Vassberg, M.A. DeHaan, S.M. Rivers, R.A. Wahls, Development of a common research model for applied CFD validationstudies, AIAA paper 6919, 2008 [Google Scholar]
- M.J. Powell, A direct search optimization method that models the objective and constraint functions by linear interpolation, in: Advances in optimization and numerical analysis, Springer, 1994, pp. 51–67 [CrossRef] [Google Scholar]
- J. Mas Colomer, N. Bartoli, T. Lefebvre, J.R. R.A. Martins, J. Morlier, An MDO-based methodology for static aeroelastic scaling of wings under non-similar flow, Struct. Multidiscipl. Optim. 63, 1045–1061 (2021) [CrossRef] [Google Scholar]
- C.W. MacCormick, The NASTRAN User’s Manual:(level 15), National Aeronautics and Space Administratio, 1972 [Google Scholar]
- J. Mas Colomer, N. Bartoli, T. Lefebvre, J.R. Martins, J. Morlier, Aeroelastic scaling of flying demonstrator: flutter matching, Mech. Ind. 22, 42 (2021) [CrossRef] [EDP Sciences] [Google Scholar]
- A. Girard, N. Roy, in: Structural dynamics in industry, John Wiley & Sons, 2010, Vol. 7 [Google Scholar]
- T.C.S. Rendall, C.B. Allen, Unified fluid-structure interpolation and mesh motion using radial basis functions, Int. J. Numer. Methods Eng. 74, 1519–1559 (2008) [Google Scholar]
Cite this article as: J. Mas Colomer, N. Bartoli, T. Lefebvre and J. Morlier, Aeroelastic scaling of flying demonstrators: mode tracking technique, Mechanics & Industry 23, 2 (2022)
All Tables
All Figures
 |
Fig. 1 Different thickness regions for modal optimization (12 in total). For each section, the thickness of the panels on the lower surface of the wing is the same as on the upper side. |
| In the text | |
 |
Fig. 2 Different stringer property regions for modal optimization (6 in total). |
| In the text | |
 |
Fig. 3 Evolution of the best found design with the number of iterations using COBYLA for N = 5. The objective function (a), the frequency constraints (b) (Eq. (3)), and the mass constraint (c) (Eq. (6)) are plotted as a function of the iterations. |
| In the text | |
 |
Fig. 4 On the left, modal results of the first optimization iteration (initial guess, in red) overlapped with the reference ones (blue). On the right, optimized modes (green) overlapped with the reference ones for the case of N = 5. |
| In the text | |
 |
Fig. 5 Evolution of the natural frequencies of the current model sorted according the best corresponding reference modes. The frequencies of the 4th and 5th modes nearly intersect around iteration 40, however their values do not cross during the optimization process. |
| In the text | |
 |
Fig. 6 Evolution of the best found design with the number of iterations using COBYLA for N = 10. The objective function (a), the frequency constraints (b) (Eq. (3)), and the mass constraint (c) (Eq. (6)) are plotted as a function of the iterations. |
| In the text | |
 |
Fig. 7 Modal results of the first optimization iteration overlapped with the reference ones for N = 10. |
| In the text | |
 |
Fig. 8 Evolution of the natural frequencies of the current model sorted according the best corresponding reference modes. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.