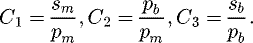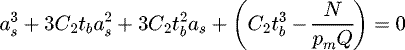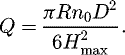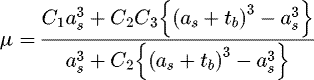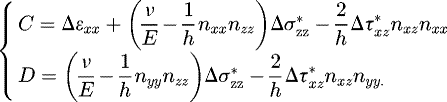| Issue |
Mechanics & Industry
Volume 23, 2022
|
|
|---|---|---|
| Article Number | 5 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/meca/2022002 | |
| Published online | 17 February 2022 | |
Regular Article
Analytical modeling of residual stress in end-milling with minimum quantity lubrication
1
Woodruff School of Mechanical Engineering, Georgia Institute of Technology, Atlanta, GA 30332, USA
2
Metal Industries Research and Development Centre (MIRDC), Kaohsiung, Taiwan
* e-mail: lingercai@gatech.edu
** e-mail: steven.liang@me.gatech.edu
Received:
11
June
2021
Accepted:
11
January
2022
Milling with minimum quantity lubrication (MQL) is now a commonly used machining technique in industry. This paper proposed an analytical model for residual stress prediction in milling with MQL based on chip formation orthogonal cutting model and boundary lubrication effect. The effect of lubrication is considered to the change of friction coefficients and the heat loss at the flank surface, which would further affect the prediction of the cutting force and temperature. The proposed model is validated with experimental data done to AZ61A magnesium alloy and obtained a reasonable validation result. The predictive results show at the case investigated, neither feed per tooth nor depth of cut has a significant influence to the general trend of residual stress, where at the surface the residual stress is highly tensile and come to compressive at deeper depth. However, the application of MQL is shown to be able to significantly reduce the average magnitude of the residual stress.
Key words: Residual stress / analytical modelling / minimum quantity lubrication
© L. Cai et al., Published by EDP Sciences 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Minimum quantity lubrication (MQL) is now a commonly used technique in industry because of its effectiveness on the cost and its sustainable features. Many researchers have proven that the application of MQL in the machining operation lowers the cutting forces, cutting temperature and it is beneficial to the performance of the finished parts as well as the tool wear [1–3]. One of the most important features of the machined part that researchers concerned is the residual stress. It affects features such as fatigue life, part distortion, and surface quality [4]. The generation of residual stress is often considered from three main sources: mechanical stresses led by plastic deformation, thermal stress led by material temperature changes, and volume changes led by phase changes of the materials [5]. The coupling effects of these three components are complex.
Many researches have been done to study residual stress generated during machining. Ding [6] gave a review of residual stress researches in grinding operation which would not be repeated here. Sharman et al. [4] performs a series of experiments to determine the effects of several cutting parameters to the residual stress generated in turning operations with Inconel 718. The most affective factor they found was the tool wear. High tensile stress was introduced with a worn tool at the surface level comparing to other cutting conditions. Jomaa et al. [7 ] investigated hard-turning operation on AISI 4340 steel with mixed ceramics inserts. They found positive correlation between the cutting speed and the tensile residual stresses at the surface. Similar positive correlation was found between the feed rate and compressive stresses. Jomaa explained these phenomenon based on a modified analytical model proposed by Loewen and Shaw [8] and a ploughing force calculation model proposed by Waldorf [9].
Likewise, the modelling of residual stress is often used by researchers as a method to understand the generation and changes of the residual stress. Ulutan et al. [10] conducted experiments in turning IN-100 and milling operation on GTD-111 with following residual stress measurements. Based on the experimental results as well as the consideration of a sinusoidal decay function, Ulutan proposed an empirical model which can further investigate the effects of cutting parameters. Numerically, based on the plane strain assumption and multiple cutting layers assumption, Guo and Liu [11] proposed a thermo-elastic-plastic FEM model to predict residual stress distribution with consideration of the effects of cutting forces, cutting temperature and clam ping forces. Outeiro et al. [12] conducted comprehensive benchmark studies to evaluate the effectiveness of several numerical predictive models with commonly used materials and a wide range of cutting conditions. They found a high dispersion among results got from the model as well as compared to the results obtained experimentally.
Comparing to other methods, analytical models usually have the advantage in time-efficiency and more profound understanding of the physics behind the phenomenon. The analytical model for the residual stress often considers elastic and plastic contacts. The mechanical loading, cutting temperature and the interaction of these two are often considered as the origin of the residual stress [13]. Liang and Su [14] treated the contact behavior as a rolling/sliding contact and therefore captured the stress history of the machined parts. They considered both the plowing region and the shearing regain as sources of the mechanical stresses. Their model is validated through experiments done with turning operation on AISI 316L and AISI 4340. Su et al. [15] then furthered their research to milling operation by considering the cutting action into axial segment with the inclination angle of each slice same as the helix angle based on Li et al.'s work [16]. This model is validated with milling data obtained in literature with Ti-6Al-4V. Wan et al. [17] proposed another way of taking helix angle into force prediction in milling operation and therefore gave an different way to model the residual stress. Their model is validated through finite element method and experimental data gained with Ti-6Al-4V. Huang et al. [18] considered the sequential effect of varying thermal-mechanical load and the approximant incremental analysis of inelastic contact to analytically model the peripheral milling, which was then validated with measurements taken on AISI 4340 steel. Zhou and Yang [19] included the sequential discontinuous variable mechanical loading feature to the end-milling model of nickel-aluminum alloy.
As for residual stresses under MQL, most researches focused on turning and grinding operations. Xavior et al. [20] experimentally investigated residual stresses with Inconel 718 with dry, MQL, and flood condition in turning operation. They found that less compressive residual stresses were induced at high cutting velocity in MQL condition. Ji et al. [21] presented an analytical model that predicts the residual stress under MQL based on Liang and Su [14] with further consideration of the lubricant effects, where the boundary lubrication theory was taken into account. De Silva et al. [22] evaluated the performance of MQL technique in grinding operation and found that in all test conditions, the application of MQL delivered compressive residual stress with highest value comparing to those in dry and other lubrication conditions. Shao et al. [23] presented an analytical model to predict residual stresses in grinding, where the effect of lubricants was reflected in the calculation of cutting force and temperature and then further applied to the rolling/sliding contact model for residual stress prediction.
For milling under MQL, Tunc et al. [24] investigated surface roughness and surface residual stress as well as tool life in robotic milling with austenitic stainless steel. The result showed that the oil flow rate affected the surface residual stresses significantly. De Paula et al. [25] performed experiments on the milling of Inconel 718 to investigated the performance of MQL comparing with conventional flood lubrication. The result suggests that the desired compressive residual stresses remained in longer length in flood cases comparing to those in MQL cases. Masmiati et al. [26] conducted experiments on end milling on S50C medium carbon steel to investigate the effect of lubricants on residual stress, cutting force and surface roughness. A mathematical model is then developed for the prediction of these factors based on response surface methodology. The proposed model showed that minimum residual stress can be achieved with flood lubrication rather than MQL.
Meanwhile, MQL has been proven to be the most effective method to improve surface roughness, diminish torque and lower temperature for some widely used magnesium alloy [27]. During the machining of magnesium alloy, chip ignition is one of the major problems [28]. While the high temperature can be significantly reduced by application of lubricants, the reactivity of magnesium to water makes this solution questionable [29]. Under this circumstance, MQL serves as a good alternative for the cooling during the machining of magnesium alloy.
Yet, there is a lack of physics-based analytical model of the residual stress in end milling operation with MQL. This article presents an analytical model to the residual stress in end milling operation based on boundary layer lubrication condition and chip formation model in orthogonal cutting. The 3D milling operation is first transferred into 2D orthogonal cutting frame, and then the cutting force and cutting temperature are calculated with effects of lubrication taken into consideration. The calculated force and temperature are then implemented to the elastic-plastic theory for residual stress calculation. The proposed model is validated with data published in literature [30,31].
2 Analytical residual stress predictive model
Figure 1 shows the flow chart of the prediction process of the proposed model. This model takes the material properties, tool geometry, cutting parameters and the lubrication condition as input and generates the residual stress distribution on the workpiece as a final output. Along the way, the cutting forces and the cutting temperature under MQL are also predicted based on previous work [32,33] . As the cutting parameters and tool geometry are inputted, the end milling operation is transferred into orthogonal cutting at each rotation angle, which will be explained in Section 2.1. The application of lubrication is considered to cause two major effects: the change of friction coefficient, briefed in Section 2.2, and the heat loss at the tool flank surface, explained in Section 2.3. The modified friction coefficient is then implemented into force calculation together with initially calculated forces and temperature with MQL consideration, as briefed in Section 2.4. These newly calculated force is then adopted into temperature calculation based on the assumption of 3 region of thermal changes, which will be briefly illustrated in Section 2.4. Then calculated forces and temperature under MQL are then served as input to the residual stress model, where a rolling/sliding contact is assumed with implement of elastic-plasticity model and hybrid algorithm. Section 2.6 gives a detailed explanation.
 |
Fig. 1 Flow chart of the residual stress calculation. |
2.1 Transferring end-milling condition into orthogonal cutting
In this model, 3D end milling condition is transferred in to 2D orthogonal cutting based on [34]. Figure 2 shows the schematic for the transformation. The average depth of cut 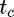 is calculated as [34]
is calculated as [34]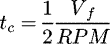 (1)where Vf is the feed rate and instantaneous equivalent depth of cut at each tool rotation angle ϕ is
(1)where Vf is the feed rate and instantaneous equivalent depth of cut at each tool rotation angle ϕ is  , where ϕ = 2πR × RPM × t at given time t.
, where ϕ = 2πR × RPM × t at given time t.
The definition of the side cutting edge angle 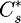 at given time t is
at given time t is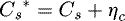 (2)where Cs is the tool side cutting angle and the chip flow angle ηc is calculated based on tool geometry and cutting parameters.
(2)where Cs is the tool side cutting angle and the chip flow angle ηc is calculated based on tool geometry and cutting parameters.
The equivalent chip flow angle 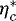 and the equivalent inclination angle i* are
and the equivalent inclination angle i* are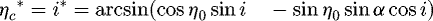 (3)where i is the inclination angle, α is the rake angle, η0 is defined as
(3)where i is the inclination angle, α is the rake angle, η0 is defined as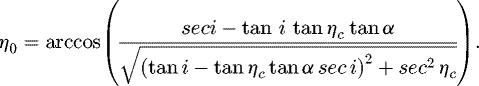 (4)
(4)
The equivalent rake angle is expressed as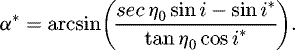 (5)
(5)
For the equivalent orthogonal cutting, the equivalent cutting depth 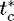 is
is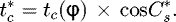 (6)
(6)
The cutting width in orthogonal cutting is related to axial depth of milling as,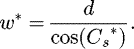 (7)
(7)
The equivalent cutting speed is a function of the rotation angle as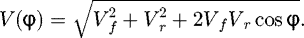 (8)where Vr = 2πR x RPM is the rotation speed and R is the tool radius.
(8)where Vr = 2πR x RPM is the rotation speed and R is the tool radius.
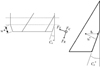 |
Fig. 2 Schematic of the transformation from 3D milling to 2D orthogonal cutting. |
2.2 Friction coefficient calculation under minimum quantity lubrication condition
Based on the assumption of uniform friction, the boundary layer lubrication effect is assumed. Figure 3 gives the schematic for it [33].
The normal load N and the friction force F at the boundary is defined as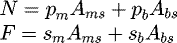 (9)where pm, sm and pb,sb are the yield pressure and shear strength at the metallic contact area and the adsorbed lubricant film contact area respectively. Ams, the metallic contact area is defined as
(9)where pm, sm and pb,sb are the yield pressure and shear strength at the metallic contact area and the adsorbed lubricant film contact area respectively. Ams, the metallic contact area is defined as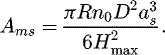 (10)
(10)
And the adsorbed lubricant film contact area Abs is defined as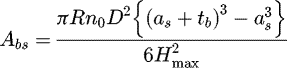 (11)where R is asperity tip radius, n0 is total asperity number, D is inclination distribution function, as is the approach of two surfaces, Hmax is the asperity height distribution, and tb is effective adsorbed lubrication film thickness. When tb = 0, it represents the dry cutting condition.
(11)where R is asperity tip radius, n0 is total asperity number, D is inclination distribution function, as is the approach of two surfaces, Hmax is the asperity height distribution, and tb is effective adsorbed lubrication film thickness. When tb = 0, it represents the dry cutting condition.
Then the friction coefficient is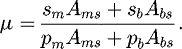 (12)
(12)
Then the friction coefficient is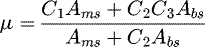 (14)
(14)
with as been solve from equation(15), the modified friction coefficient μ is then calculated through equation (17). This method helps to consider the effect of MQL. The changes of lubrication can be represented in the calculation of friction coefficient, where the conventional machining is also considered (dry machining). However, while the flooded case can also be assumed as a uniform friction case, it does not fit the assumption for the boundary layer condition, where the lubricant thickness would be small.
2.3 Heat loss under MQL condition in orthogonal cutting
Temperature drop would occur as MQL would create heat loss at the flank cutting surface. Then heat loss intensity qhl can be expressed as a constant multiplying the difference between the average tool flank face temperature Tflank and the room temperature Tw as following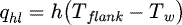 (18)where
(18)where 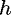 is the average heat transfer coefficient, which is estimated by the Nusselt number as following
is the average heat transfer coefficient, which is estimated by the Nusselt number as following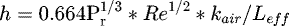 (19)
(19)
where Pr is the Prandtl number, Re is the Reynolds number, kair is the thermal conductivity of the air and Leff is the effective lubricated length.
2.4 Force calculation in end milling with friction coefficient calculated based on MQL
As shown in Figure 2, the force calculation is first calculated with chip formation orthogonal model, whose result are used for the friction coefficient calculation. A more accurate result is delivered by the modified chip formation orthogonal model, also called modified Oxley's model [35].
The modified model takes workpiece material into account with implement of Johnson-Cook material model, which gives an empirical relationship for the flow stress σ of a material as follows: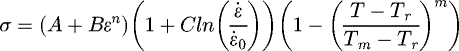 (20)where ϵ is the equivalent strain,
(20)where ϵ is the equivalent strain, 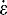 is the equivalent strain rate, and
is the equivalent strain rate, and 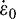 is the reference strain rate, which is usually taken as 1s−1. T is the instantaneous temperature of the material. Tm is the melting point of the material. Tr is the environmental temperature. A, B, C, n and m are constants gained through empirical methods.
is the reference strain rate, which is usually taken as 1s−1. T is the instantaneous temperature of the material. Tm is the melting point of the material. Tr is the environmental temperature. A, B, C, n and m are constants gained through empirical methods.
As plain strain condition is assumed, the Von Mises criterion is applied. This leads to the equivalent shear stress kab at the shear plane is expressed as follows: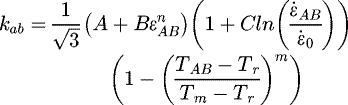 (21)where ϵAB is the equivalent strain on the shear plane,
(21)where ϵAB is the equivalent strain on the shear plane, 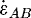 is the equivalent strain rate on the shear plain, and TAB is the temperature on the shear plane.
is the equivalent strain rate on the shear plain, and TAB is the temperature on the shear plane.
The detailed modified chip formation orthogonal cutting model has been developed in recent decades and been applied to various cases [33]. The detail would not be repeated here.
2.5 Temperature calculation in end milling with MQL
The temperature calculation considers 3 major sources that lead to temperature source: the primary heat source caused by shear deformation, the secondary heat source led by tool-workpiece interface, and a heat loss at the flank tool surface caused by the cooling effect of the lubricants. Figure 4 gives an illustration to the sources [33].
At point (X,Z) on the workpiece, the temperature rises in the workpiece from the primary heat source is calculated as following: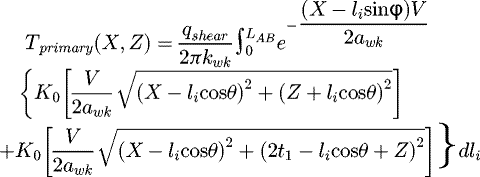 (22)where L is the length of the shear plane, given by
(22)where L is the length of the shear plane, given by 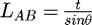 . θ is the shear angle and t1 is the undeformed chip thickness. φ is given as
. θ is the shear angle and t1 is the undeformed chip thickness. φ is given as 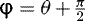 . V is the cutting speed. awk is the thermal diffusivity of the workpiece. kwk is the thermal conductivity of the workpiece. K0 is the modified Bessel function. qshear is the heat source density in the shear zone, given as following:
. V is the cutting speed. awk is the thermal diffusivity of the workpiece. kwk is the thermal conductivity of the workpiece. K0 is the modified Bessel function. qshear is the heat source density in the shear zone, given as following: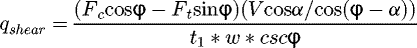 (23)where α is the rake angle and w is the cutting width.
(23)where α is the rake angle and w is the cutting width.
The temperature rise in the secondary heat source here is calculated as following: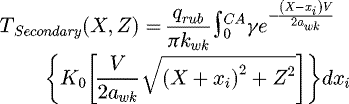 (24)where CA is the contact length calculated based on slip-line model [36]. γ is the heat distribution coefficient based on material properties of the workpiece and the cutting tool. γ is defined as following:
(24)where CA is the contact length calculated based on slip-line model [36]. γ is the heat distribution coefficient based on material properties of the workpiece and the cutting tool. γ is defined as following: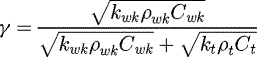 (25)where kwk the thermal conductivity of the workpiece, ρwk is the density of the workpiece and Cwk is the thermal capacity of the workpiece. kt, ρt, Ct are the same properties of the cutting tool respectively. qrub is the heat source density in the rubbing zone, given as following:
(25)where kwk the thermal conductivity of the workpiece, ρwk is the density of the workpiece and Cwk is the thermal capacity of the workpiece. kt, ρt, Ct are the same properties of the cutting tool respectively. qrub is the heat source density in the rubbing zone, given as following: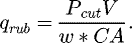 (26)
(26)
In which Pcut i the plowing force in the cutting condition, which can be calculated based on Waldorf's [36].
The generated heat loss at this region is calculated as follows: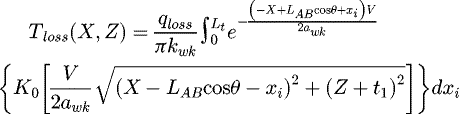 (27)where qloss is the heat loss intensity due to air-oil flow, given by equation (18).
(27)where qloss is the heat loss intensity due to air-oil flow, given by equation (18).
2.6 Residual stress calculation in end milling with MQL
2.6.1 Mechanical stresses
A rolling/sliding contact approach is adapted in this model which is developed in [15]. Both the contact region of the tool tip to the workpiece and the shear zone are considered as sources of the mechanical stresses. Figure 5 gives an illustration of the sources of the mechanical stresses.
The system is firstly assumed to be elastic deformed only. Figure 6 shows the schematic of the boundary stresses proposed by Johnson [37]. The mechanical stresses are calculated as equation (28).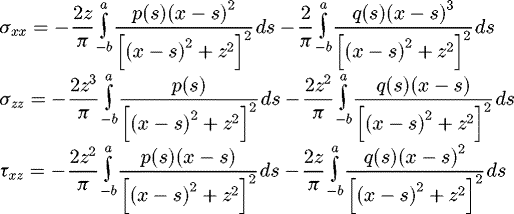 (28)where p (s) is the normal loading stress and q (s) is the tangential loading stress. Both stresses comes from two sources mentioned before, namely the contact region and the shear zone.
(28)where p (s) is the normal loading stress and q (s) is the tangential loading stress. Both stresses comes from two sources mentioned before, namely the contact region and the shear zone.
The normal loading from the contact pcont is calculated as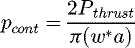 (29)where Pthrust is the normal plowing force calculated based on [36]. w* is equivalent cutting width calculated in equation (7). a is the contact length showed in Figure 6. The normal loading from shear zone pshear is calculated as
(29)where Pthrust is the normal plowing force calculated based on [36]. w* is equivalent cutting width calculated in equation (7). a is the contact length showed in Figure 6. The normal loading from shear zone pshear is calculated as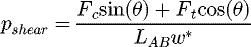 (30)where Fc and Ft are the normal and tangential forces. θ is the shear angle LAB is the shear length. All of these are calculated in chip formation cutting model.
(30)where Fc and Ft are the normal and tangential forces. θ is the shear angle LAB is the shear length. All of these are calculated in chip formation cutting model.
The tangential loading from contact qcont is calculated as following: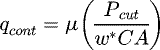 (31)where Pcut is the plowing force in cutting direction. μ is modified friction coefficient obtained from Section 2.2. The tangential loading from shear zone qshear is assumed to be the same as the flow stress on shear plane calculated in equation (21).
(31)where Pcut is the plowing force in cutting direction. μ is modified friction coefficient obtained from Section 2.2. The tangential loading from shear zone qshear is assumed to be the same as the flow stress on shear plane calculated in equation (21).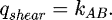 (32)
(32)
Calculated pcont, pshear,qcont,qshear are substituted in to equation (28) individually to get corresponding stresses. However, the results calculated from shearing are not in the workpiece coordinate. A coordinate transformation needs to be applied, which is constructed as following.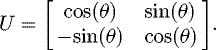 (33)
(33)
The final mechanical stress is the addition of the calculated stresses in the workpiece coordinate.
2.6.2 Thermal stresses
The sources of the thermal stress are considered in three parts: the thermal loads in X and Z direction, the surface tension caused by temperature changes and the hydrostatic pressure.
Thermal stresses at any point on the workpiece can be calculated with equation (34). E is the Young's modulus, and υ is the Poisson's ratio. K, ρ, Cp are the thermal conductivity, density and the specific heat of the material. Gxh, Gxv, Gzh, Gzv, Gxzh, Gxzv are the Green's function that represents the plane stain, whose detailed expression can be found in [38].
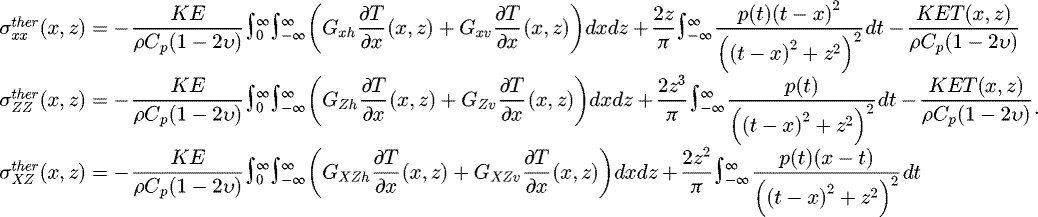 (34)
(34)
2.6.3 The total elastic stress
The total elastic stress is the matrix addiction of the mechanical stress and the thermal stress.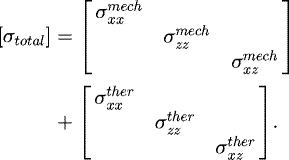 (35)
(35)
2.6.4 Elastic-plastic incremental model
There two possible states for a point at the workpiece in the machining process. If the load on this point is within the elastic limit of the workpiece, the Hooke's law can be used for the strain data. As the loads exceeds the elastic limit, the plastic deformation occurs. The Von-Miss criterion is used for the determination of the yield criterion, which is expressed as following: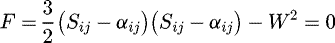 (36)where
(36)where 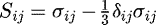 is the deviatoric stresses. δij is the Kronecker symbol. αij = Sklnklnij is the deviatoric back stresses. ⟨⟩ is defined as x = (x + |x|). nij is the unit normal vector in plastic strain rate direction, which is defined as
is the deviatoric stresses. δij is the Kronecker symbol. αij = Sklnklnij is the deviatoric back stresses. ⟨⟩ is defined as x = (x + |x|). nij is the unit normal vector in plastic strain rate direction, which is defined as 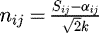 , where k is the average flow stress calculated based on equation (20). W here is the uniaxial normalized radius of the yield surface.
, where k is the average flow stress calculated based on equation (20). W here is the uniaxial normalized radius of the yield surface.
The effective strain and strain rate are defined as following:
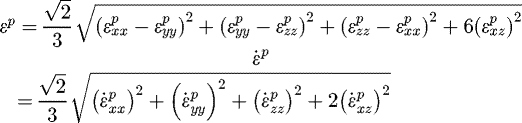 (37)
(37)
If the yielding does not occur, the loading process would be considered as elastic. If the yielding occurs, the strain increment on the yield surface is formulated based on the plastic flow rule, which is then expressed as: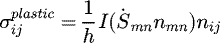 (38)where h is the plastic modulus function.
(38)where h is the plastic modulus function.
For nonlinear workhardening matierals, the blending function Ψ is applied here based on McDowell [39].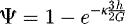 (39)where κ is an algorithm constant and
(39)where κ is an algorithm constant and 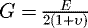 is the elastic shear modulus.
is the elastic shear modulus.
Then the strain increment in x and y direction can be expressed in equation (40).
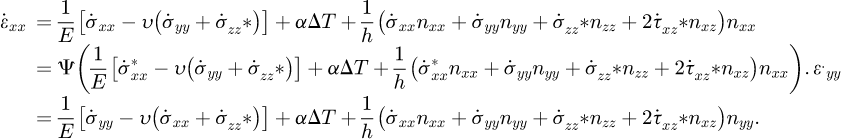 (40)
(40)
Based on Merwin and Johnson [40], a relaxation procedure is adopted to meet the boundary condition, where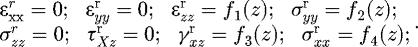 (41)
(41)
The stress and strain increments for M relaxation steps is following: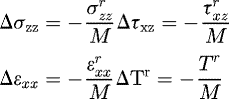 (42)Where Tr is the remaining temperature rise.
(42)Where Tr is the remaining temperature rise.
In the relaxation procedure, the yield could also occur, which requires a determination of the occurrence. The Von Mises criterion is also used here. For elastic relaxation, when F ≤ 0 and 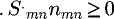 , the increment is expressed as
, the increment is expressed as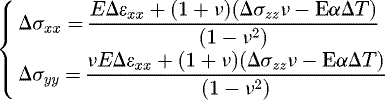 (43)
(43)
For plastic relaxation, the increment is expressed as
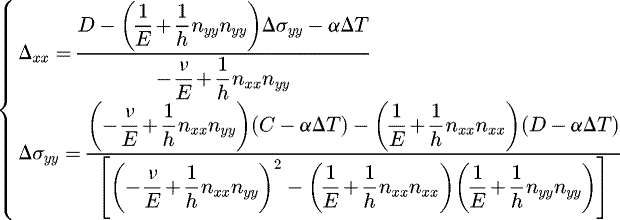 (44)
(44)
3 Experimental data validation
The proposed model is validated with data published in literature. Chirita et al. [30] performed experiments on AZ61A magnesium alloy with dry, MQL and compressed air conditions. The experimental residual stress data were first published in 2014, with further analysis published in 2015. This paper uses information from both articles to elaborate the understanding to the experiments. The experiments were performed on a Rapimill 700 CNC Machine Center, with a cutting tool of 50 mm diameter. The inserts used were Sandvik Coromat 490R-09T304EML H13A uncoated carbide inserts. The material is AZ61A magnesium alloy cylindrical part with diameter of 80 mm. The MQL system was produce by SKF. Figure 7 shows the set-up of the experiment set-up. The experiments performed milling under different cutting parameters. The compressed air cases are not included in this article. For both Dry and MQL condition, experiments were done with depth of cut 0.2 and 0.5 mm, feed per tooth as 0.05 and 0.2 mm/tooth, and cutting speed of 600 and 1600 m/min. The experimental condition is shown in Table 1.
The measurement of the residual stress used SINT-Restan MTS300 system and HBM 1-RY61-1.5/120M strain gages for the incremental hole drilling method. Both the maximum and the minimum principal residual stress were calculated and reported. The principal residual stresses are calculated as: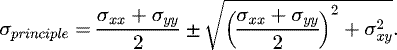 (46)
(46)
As the Johnson-Cook model is used in the proposed model for material properties, yet the exact properties are not published in found literature. Johnson-Cook constants obtained from a similar material AZ31B magnesium alloy are used in the model validation. Table 2 gives the material properties of AZ31B, which is used in this case.
Figure 8 shows the comparison of the prediction of the proposed model to the experimental data with the average principle stress at both Dry and MQL cases with feet per tooth 0.2 mm and depth of cut 0.5 mm and cutting speed 1600 m/min. As detected in the experiment, in both dry and MQL cases, the proposed model gives mostly compressive residual stress prediction on the workpiece. For the dry case, the maximum compressive residual stress in experiment is at 0.05 mm below the surface with a value of −35.75 MPa. The proposed mode predicts the maximum compressive residual stress occurs at 0.047 mm below the surface with a value of −46.85 MPa. For the MQL cases, the experiment gives the maximum compressive residual stress at 0.05 mm with a value of −58.5 MPa, while the proposed model gives the most compressive value at 0.032 mm below the surface with a value of −46.25 MPa. The proposed model also gives prediction to the surface residual stress, which is not measured in the experiment. The proposed model does predict a significant difference between the Dry and MQL cases on the absolute value of the maximum residual stress below the surface. However, it shows that the application of MQL significantly reduces the average residual stress on the workpiece. Another noticeable thing is that the proposed model gives several points where the residual stress would be tensile, which is not shown in the experimental data. This could be explained by the initial residual stress remained in the workpiece even before the experiments starts. The initial residual stress is also reported in the literature [30]. However, the initial status of the material is considered of zero residual stress in the model.
Figure 9 shows the comparison between the predictive data and the experimental data under MQL with feed per tooth of 0.2 mm and depth of cut 0.5 mm with different cutting velocity, 600 and 1600 m/min. As shown in graph, the proposed model gives a mostly compressive residual stress prediction, which is same as the experimental data. With cutting velocity to be 600 m/min, the experimental data gives the most compressive residual stress at 0.05 mm below the surface with a value of −51.5 MPa, while the model predicts that point at 0.047 mm with a value of −47.7 MPa. When cutting speed is 1600 m/min, the measurement gives a value of −58.5 MPa at 0.05 mm below the surface, while the model suggests −46.85 MPa at 0.047mm below the surface. It can be seen that, as the experimental data suggest, the proposed model also predicts that, at this cutting condition, the change of cutting velocity under MQL does not significantly affect neither the absolute value nor the position of where the highest compressive residual stress occurs. Besides the prediction of the surface residual stress, which is not included in the experiments, the proposed model also gives a faster convergence to the equilibrium stress than the measurements in the experiment. This can also be explained by the introduction of the initial residual stress as mentioned before.
So far, the proposed model gives a reasonable match to the experimental condition. Some further analysis was also done to explore the influence of other cutting parameters to the residual stress based on the proposed model.
Figure 10 shows the investigation to the residual stress at cutting velocity of 1600 m/min and depth of cut 0.5 mm with different feed per tooth at MQL condition. The prediction shows that smaller feed per tooth introduces a smaller magnitude of the residual stress with comparison of ft 0.2 mm and ft 0.15 mm. However, as the feet per tooth is really small, the decrease in feed per tooth would not have significant influence to the residual stress prediction. Another influence of the decreasing feed per tooth is the faster convergence rate of the residual stress. As shown in Figure 10, as smaller feed per tooth is applied (0.15 mm), the residual stress magnitude went back to zero faster than the bigger feed case (0.2mm). This also leads to an obvious decrease in the average residual stress below the surface.
Figure 11 shows the investigation of the influence of the depth of cut to the residual stress. The proposed model provides residual stress results at cutting velocity of 1600 m/min, feed per tooth 0.2 mm with different depth of cut: 0.5, 0.45, 0.4, and 0.35 mm. the predictive results show little difference between each other in the general trend of residual stress. However, significant difference were found at the surface.
It is found that both feed per tooth and depth of cut has little influence to the prediction results. As showed in Figure 9, the change of cutting velocity at this case does not have a significant influence to the residual stress distribution trend neither. One possible explanation is because of the high thermal conductivity of the magnesium alloy. Because of this, the heat generation of the changing cutting parameter is limited by the application to the lubricant, which added a heat loss to the total temperature filed. The prediction of the temperature filed also shows a limited temperature rise. However, the experiment data does not contain temperature information. The discussion of temperature would need more experimental validation to this specific case.
 |
Fig. 8 Comparison of the predictive data to experimental data at fz = 0.2 mm and depth of cut = 0.5 mm with both Dry and MQL. |
 |
Fig. 9 Comparison of the predictive data to experimental data at fz = 0.2mm and depth of cut = 0.5 mm under MQL with different cutting velocity. |
 |
Fig. 10 Investigation of the residual stress under MQL with cutting velocity 1600 m/min, depth of cut 0.5mm at different feed per tooth. |
 |
Fig. 11 Investigation of the residual stress under MQL with cutting velocity 1600 m/min, feed per tooth 0.2 mm at different depth of cut. |
4 Discussion and conclusions
In this paper, an analytical model has been proposed for the prediction of residual stress in milling operation. The milling operation is first transferred into orthogonal cutting condition, where the cutting force and cutting temperature will be predicted. The effects of MQL is regarded in two parts: decreasing friction coefficient and extra heat loss. Both effects are affective to the prediction of the force and temperature. The force and temperature without MQL are calculated based on chip formation model and then utilized to get the modified friction coefficient. Based on the assumption of uniform friction, the boundary layer lubrication model is used to modify the friction coefficient at the interface. The calculated friction coefficient is then applied back to the modified chip formation model for the force calculation with MQL. As the force is calculated, a true temperature field can be obtained. The force and temperature field calculated are inputted to the residual stress model, which is based on rolling\sliding contact assumption. The elastic stress is calculated, considering both the contact area of the tool and the workpiece and the shear zone as the sources of the stresses. The Von Mises criterion is used for the determination of the elastic-plastic situation, where different loading and relaxation procedure is applied accordingly.
Then the proposed model is validated with published experimental data with AZ61A magnesium alloy and gained a reasonable prediction result comparing to the experiment. The proposed model is then used for the investigation of the influence of different cutting parameters to the milling of AZ61Z magnesium alloy. Here are some conclusions to draw:
The application of the MQL does not necessarily have a significant effect on the maximum value of the compressive residual stress, but gives a much smaller average residual stress value under the workpiece surface.
Under MQL condition, the change in the cutting velocity at this case does not lead to significant difference to the prediction of the residual stress. Neither does the change of depth of cut.
Decreased feed per tooth with MQL condition leads to less residual stress to a degree. However, after certain limit, the decreasing does not have effects neither.
Overall, the application of MQL does affect the residual stress and lead it to a more compressive direction. The proposed model gives a fair prediction to the experiment mentioned in the article. More application of the model can be done with more experimental data with other materials.
Conflict of interest
All authors do not have conflict of interest to this submission.
Funding Information
This word is supported by Metal Industries Research and Development Centre (MIRDC), Kaohsiung, Taiwan.
References
- M. Li, T. Yu, R. Zhang, L. Yang, H. Li, W. Wang, MQL milling of TC4 alloy by dispersing graphene into vegetable oil-based cutting fluid, Int. J. Adv. Manufactur. Technol. 99, 1735–1753 (2018) [CrossRef] [Google Scholar]
- M.A. Bashir, M. Mia, N.R. Dhar, Investigations on surface milling of hardened AISI 4140 steel with pulse jet MQL applicator, J. Inst. Eng. Ser. C 99, 301–314 (2016) [Google Scholar]
- L.R. da Silva, D.A. da Silva, F.V. dos Santos, F.J. Duarte, Study of 3D parameters and residual stress in grinding of AISI 4340 steel hardened using different cutting fluids, Int. J. Adv. Manufactur. Technol. 100, 895–905 (2018) [Google Scholar]
- A.R.C. Sharman, J.I. Hughes, K. Ridgway, An analysis of the residual stresses generated in Inconel 718 (TM) when turning, J. Mater. Process Tech. 173, 359–367 (2006) [CrossRef] [Google Scholar]
- J.-g. Li, S.-q. Wang, Distortion caused by residual stresses in machining aeronautical aluminum alloy parts: recent advances, Int. J. Adv. Manufactur. Technol. 89, 997–1012 (2016) [Google Scholar]
- W. Ding, L. Zhang, Z. Li, Y. Zhu, H. Su, J. Xu, Review on grinding-induced residual stresses in metallic materials, Int. J. Adv. Manufactur. Technol. 88, 2939–2968 (2016) [Google Scholar]
- W. Jomaa, V. Songmene, P. Bocher, An investigation of machining-induced residual stresses and microstructure of induction-hardened AISI 4340 steel, Mater. Manufactur. Process. 31, 838–844 (2015) [Google Scholar]
- E.G. Loewen, M.C. Shaw, On the Analysis of Cutting Tool Temperatures, Transactions of the ASME 76, 217–231 (1954) [Google Scholar]
- D.J. Waldorf, A simplified model for ploughing forces in turning, J. Manufactur. Process. 8, 76–82 (2006) [CrossRef] [Google Scholar]
- D. Ulutan, Y.M. Arisoy, T. Özel, L. Mears, Empirical modeling of residual stress profile in machining nickel-based superalloys using the sinusoidal decay function, Proc. CIRP 13, 365–370 (2014) [CrossRef] [Google Scholar]
- Y.B. Guo, C.R. Liu, Fem analysis of mechanical state on sequentially machined surfaces, Mach. Sci. Technol. 6, 21–41 (2002) [CrossRef] [Google Scholar]
- J.C. Outeiro, D. Umbrello, R. M'Saoubi, I.S. Jawahir, Evaluation of present numerical models for predicting metal cutting performance and residual stresses, Mach. Sci. Technol. 19, 183–216 (2015) [CrossRef] [Google Scholar]
- M. Wan, X.-Y. Ye, D.-Y. Wen, W.H. Zhang, Modeling of machining-induced residual stresses, J. Mater. Sci. 54, 1–35 (2018) [Google Scholar]
- S.Y. Liang, J.C. Su, Residual stress modeling in orthogonal machining, CIRP Ann. 56, 65–68 (2007) [CrossRef] [MathSciNet] [Google Scholar]
- J.-C. Su, K.A. Young, K. Ma, S. Srivatsa, J.B. Morehouse, S.Y. Liang, Modeling of residual stresses in milling, Int. J. Adv. Manufactur. Technol. 65, 717–733 (2012) [Google Scholar]
- H.Z. Li, W.B. Zhang, X.P. Li, Modelling of cutting forces in helical end milling using a predictive machining theory, Int. J. Mech. Sci. 43, 1711–1730 (2001) [CrossRef] [Google Scholar]
- M. Wan, X.-Y. Ye, Y. Yang, W.-H. Zhang, Theoretical prediction of machining-induced residual stresses in three-dimensional oblique milling processes, Int. J. Mech. Sci. 133, 426–437 (2017) [CrossRef] [Google Scholar]
- X. Huang, X. Zhang, H. Ding, An enhanced analytical model of residual stress for peripheral milling, Proc. CIRP 58, 387–392 (2017) [CrossRef] [Google Scholar]
- R.H. Zhou, W.Y. Yang, Analytical modeling of residual stress in helical end milling of nickel-aluminum bronze, Int. J. Adv. Manuf. Tech. 89, 987–996 (2017) [CrossRef] [Google Scholar]
- M. Anthony Xavior, M. Manohar, P.M. Madhukar, P. Jeyapandiarajan, Experimental investigation of work hardening, residual stress and microstructure during machining Inconel 718, J. Mech. Sci. Technol. 31, 4789–4794 (2017) [CrossRef] [Google Scholar]
- X. Ji, X. Zhang, S.Y. Liang, Predictive modeling of residual stress in minimum quantity lubrication machining, Int. J. Adv. Manufactur. Technol. 70, 2159–2168 (2013) [Google Scholar]
- L.R. da Silva, E.C. Bianchi, R.Y. Fusse, R.E. Catai, T.V. França, P.R. Aguiar, Analysis of surface integrity for minimum quantity lubricant—MQL in grinding, Int. J. Mach. Tools Manufact. 47, 412–418 (2007) [CrossRef] [Google Scholar]
- Y. Shao, O. Fergani, B. Li, S.Y. Liang, Residual stress modeling in minimum quantity lubrication grinding, Int. J. Adv. Manufactur. Technol. 83, 743–751 (2015) [Google Scholar]
- L.T. Tunc, Y. Gu, M.G. Burke, Effects of Minimal Quantity Lubrication (MQL) on surface integrity in robotic milling of austenitic stainless steel, Proc. CIRP 45, 215–218 (2016) [CrossRef] [Google Scholar]
- G. de Paula Oliveira, M. Cindra Fonseca, A.C. Araujo, Analysis of residual stress and cutting force in end milling of Inconel 718 using conventional flood cooling and minimum quantity lubrication, Int. J. Adv. Manufactur. Technol. 92, 3265–3272 (2017) [CrossRef] [Google Scholar]
- N. Masmiati, A.A.D. Sarhan, M.A.N. Hassan, M. Hamdi, Optimization of cutting conditions for minimum residual stress, cutting force and surface roughness in end milling of S50C medium carbon steel, Measurement 86, 253–265 (2016) [CrossRef] [Google Scholar]
- S. Bhowmick, M.J. Lukitsch, A.T. Alpas, Dry and minimum quantity lubrication drilling of cast magnesium alloy (AM60), Int. J. Mach. Tool Manu. 50, 752–752 (2010) [CrossRef] [Google Scholar]
- R. Viswanathan, S. Ramesh, V. Subburam, Measurement and optimization of performance characteristics in turning of Mg alloy under dry and MQL conditions, Measurement 120, 107–113 (2018) [CrossRef] [Google Scholar]
- D. Carou, E.M. Rubio, C.H. Lauro, J.P. Davim, The effect of minimum quantity lubrication in the intermittent turning of magnesium based on vibration signals, Measurement 94, 338–343 (2016) [CrossRef] [Google Scholar]
- B. Chirita, Study of residual stresses distribution generated from milling of magnesium alloy parts, Appl. Mech. Mater. 657, 18–22 (2014) [CrossRef] [Google Scholar]
- B. Chirita, G. Mustea, G. Brabie, A statistical analysis applied for optimal cooling system selection and for a superior surface quality of machined magnesium alloy parts, Proc. Inst. Mech. Eng. B 229, 392–408 (2014) [Google Scholar]
- X. Ji, Zhang, X. Liang, A new approach to predict machining force and temperature with minimum quantity lubrication, in: ASME 2012 International Manufacturing Science and Engineering Conference (2012) 69–76 [CrossRef] [Google Scholar]
- Y. Feng, X. Lu Liang, Analytical and Numerical Predictions of Machining-Induced Residual Stress in Milling of Inconel 718 Considering Dynamic Recrystallization (2018) [Google Scholar]
- P.L.B. Oxley, The Mechanics of Machining: An Analytical Approach to Assessing Machinability (1989) [Google Scholar]
- Y. Chen, H.Z. Li, J. Wang, Further development of oxley's predictive force model for orthogonal cutting, Mach. Sci. Technol. 19, 86–111 (2015) [Google Scholar]
- D.J. Waldorf, R.E. DeVor, S.G. Kapoor, A slip-line field for ploughing during orthogonal cutting, J. Manuf. Sci. E 120, 693–699 (1998) [CrossRef] [Google Scholar]
- K.L. Johnson, Contact mechanics, Cambridge University Press, Cambridge, 1985 [CrossRef] [Google Scholar]
- M.T.A. Saif, C.Y. Hui, A.T. Zehnder, Interface shear stresses induced by non-uniform heating of a film on a substrate, Thin Solid Films 224, 159–167 (1993) [CrossRef] [Google Scholar]
- D.L. McDowell, Stress state dependence of cyclic ratchetting behavior of two rail steels, Int. J. Plasticity 11, 397–421 (1963) [Google Scholar]
- J.E. Merwin, K.L. Johnson, An analysis of plastic deformation in rolling contact, Proc. Inst. Mech. Eng. B 177, 676–690 (1963) [CrossRef] [Google Scholar]
- F. Abbassi, M. Srinivasan, C. Loganathan, R. Narayanasamy, M. Gupta, Experimental and numerical analyses of magnesium alloy hot workability, J. Magnes. Alloy 4, 295–301 (2016) [CrossRef] [Google Scholar]
Cite this article as: L. Cai, Y. Feng, S.Y. Liang, Analytical modeling of residual stress in end-milling with minimum quantity lubrication, Mechanics & Industry 23, 5 (2022)
All Tables
All Figures
 |
Fig. 1 Flow chart of the residual stress calculation. |
| In the text | |
 |
Fig. 2 Schematic of the transformation from 3D milling to 2D orthogonal cutting. |
| In the text | |
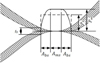 |
Fig. 3 Schematic for boundary layer lubrication effect [32]. |
| In the text | |
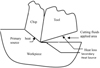 |
Fig. 4 Illustration of considered heat change regions [16]. |
| In the text | |
 |
Fig. 5 Schematic of mechanical stresses sources [15]. |
| In the text | |
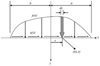 |
Fig. 6 Illustration of the boundary stresses [37]. |
| In the text | |
 |
Fig. 7 Experiment set-up [31]. |
| In the text | |
 |
Fig. 8 Comparison of the predictive data to experimental data at fz = 0.2 mm and depth of cut = 0.5 mm with both Dry and MQL. |
| In the text | |
 |
Fig. 9 Comparison of the predictive data to experimental data at fz = 0.2mm and depth of cut = 0.5 mm under MQL with different cutting velocity. |
| In the text | |
 |
Fig. 10 Investigation of the residual stress under MQL with cutting velocity 1600 m/min, depth of cut 0.5mm at different feed per tooth. |
| In the text | |
 |
Fig. 11 Investigation of the residual stress under MQL with cutting velocity 1600 m/min, feed per tooth 0.2 mm at different depth of cut. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.