| Issue |
Mechanics & Industry
Volume 18, Number 6, 2017
|
|
|---|---|---|
| Article Number | 604 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/meca/2016087 | |
| Published online | 02 February 2018 | |
Research Article
Fatigue resistance of randomly oriented short glass fiber reinforced polyester composite materials immersed in seawater environment
1
Civil Engineering Laboratory, Civil Engineering Department, Badji Mokhtar University,
PO Box
12,
23000
Annaba, Algeria
2
Civil Engineering Department, Med Seddik Benyahia University,
18000
Jijel, Algeria
* e-mail: bredjel@yahoo.fr
Received:
29
August
2016
Accepted:
21
December
2016
Randomly oriented short fiber mat reinforced polyester composite laminates immersed in natural seawater for various periods were tested in static and cyclic fatigue loading under three-point bending conditions. Water absorption increased the weight of the specimen while the extraction of soluble compounds induces a weak weight loss. Wöhler curves carried out from repetitive fatigue tests were drawn for the different periods of immersion time. These curves, which are characterized by an important and a significant scatter in their lifetime, were modeled by straight lines. These glass-polyester laminates deteriorate in fatigue tests at a constant rate by cycle decade. This rate increases with increasing immersion time in seawater at a constant speed. A comparison between different mathematical models of endurance curves shows that Wöhler's equation gives a good representation of the average part of the curve.
Key words: Seawater / polyester / fatigue / Wöhler’s curve / damage
© AFM, EDP Sciences 2017
1 Introduction
A fiber reinforced epoxy resin composite has a series of sound properties, such as high specific strength, high resistance to seawater corrosion, anti-adhesion of biological forms, and absorbing impact energy [1]. Therefore, a composite of this kind is a promising material for applications in the shipping industry. Likewise, unidirectional or randomly directioned glass fiber reinforced polyester or epoxy resin are commonly used as lightweight materials in a wide variety of marine applications. However, these laminated composite materials are also very susceptible and sensitive to damage induced by the environment, which degrades severely their physical and mechanical properties [2,3]. Some interesting studies on the effects of environmental conditions on the behavior of composite materials have been reported in recent decades [4–8]. Wide-scale usage of glass reinforced polymers is seriously hindered by the lack of experimental data and understanding of the durability aspect in the seawater environment [9]. Therefore, to assume long-term durability, a fundamental understanding is essential in terms of strength and material degradation.
It clearly appear that in the seawater environment and for marine applications, the degradation of the properties of the composite materials, which undergo damage after long-term service, is inevitable and their resistance to climatic aging, notably for those covered with gel coating, is unequal, which constitutes an obstacle preventing their extensive use [10,11]. Consequently, it is essential to understand how these materials behave during long-term applications. All the studies performed in this domain have reported that water absorption constitutes an important parameter in the degradation process of polymer compounds applied in marine domains. The gain in water content increases the probability of the material's degradation. The water absorption and longevity of composites based on polyester or epoxy resin for marine applications correlated to executive mechanical modifications have been the subject of various investigations [12,13]. Gautier et al. [14] report that the mechanical degradation of polyester resins is not only the consequence of hydrolytic aging but is principally caused by cracks and blisters. Generally, numerous environmental factors at the origin of the initiation and the development of damage in composite materials are present in real service states. Therefore it seems essential that the composite materials retain their mechanical properties with less degradation in a humid environment or when exposed to water. The fatigue behavior of randomly oriented short fiber mat reinforced laminated composite materials is still less well understood than the behavior of unidirectional composites. Several studies have been devoted to the prediction and characterization of the fatigue behavior of these composite materials in order to develop improved analytical and experimental methods and therefore to establish efficient and reliable models to predict fatigue mechanical behavior during the lifetime with good probability.
Generally, the fatigue of composites materials is a complex phenomenon and the failure mechanisms during the fatigue process are still not completely understood and are at present the subject of numerous investigations.
The damage that it initiates is diffuse and has mechanisms which are numerous or difficult to identify and quantify. The properties of these materials show a progressive loss of resistance and stiffness with a significant increase of their damping. This makes it complex and difficult to model and predict the lifetime. The accumulation of damage resulting from repeated impact loads was studied by Mouritz et al. [15], who report that microscopy revealed the formation of deep craters at the point of application of the load and an increase in size with the number of impacts. Similarly, Wu and Shyu [16] and Found and Howard [17] show the effect of the number of impacts for different loads on the composite surface. Ray et al. [18,19], examining the properties of composite materials in repeated impacts loading using the E–Nf curves (amount of impact energy-impact failure fatigue) report that the strength and the number of impacts are the two main parameters that govern the behavior of these materials in fatigue. Furthermore, the effect of moisture on the properties of glass fiber reinforced composite materials is an important issue, since such environmental factors are generally present in actual service conditions [20].
To investigate the influence of the mechanical properties of glass fiber or kevlar reinforced epoxy matrix laminates on the fatigue and damage behavior, new predictive models have been developed [21]. However they still need to be validated through experimental data.
From a phenomenological perspective, the fatigue behavior of a large variety of sandwich structures and laminated composite materials can be analyzed and evaluated by looking at the global stiffness, residual stresses and other quantifiable mechanical characteristics of damage. These interesting studies have also evaluated the stiffness degradation during the fatigue history as a significant quantitative indicator of the cumulative damage in cyclic loading [22–25]. So the stiffness degradation versus the number of cycles generated during the fatigue loading is generally used as a metric parameter for the level and the quantity of damage in sandwich structures and laminate composite materials in fatigue. Modeling approaches using empirical functions with the identification of interpolation coefficients have been formulated to describe the complete evolution of the loss of stiffness [26]. An analytical predictive model to identify the cyclic fatigue behavior of sandwich panels made from CFRP has been developed and proposed recently [27]. This approach reduces significantly the number of experimental loading levels required for identification and allows an efficient fatigue design model that can predict the fatigue endurance through an alternative formulation of the stiffness degradation. The model can also be used for other loading conditions.
The aim of this experimental work is to investigate the direct effects of the immersion time in a natural seawater environment on the fatigue performance of glass fiber reinforced unsatured polyester resin laminates subjected to cyclic fatigue loading under three-point loading conditions. A series of fatigue test measurements was performed on samples at different values of loading levels rd, defined as the ratio of the minimum fatigue strength (which is equal to zero in this study) to the maximum fatigue strength. This composite laminate produced by a unit of UPS Chlef (Algeria) is used in a wide variety of marine and agriculture applications such as barks, canoes, patrol boats, fishing boats and liquid conducting irrigation pipes in the agricultural domain. The loading level versus the number of cycles generated during the total fatigue history is a metric for the establishment of Wöhler curves. The characterization of the laminates under cyclic loading in fatigue bending is discussed in terms of endurance and fatigue resistance. The rupture of the specimens after fatigue and aging was examined for a better understanding of different phenomena (debonding, delamination and fracture of matrix and fibers) that occur in the material during the fatigue history. Furthermore, the quasi-static behavior of the untreated laminate under three-point bending is also described and analyzed.
2 Experimental protocol
The material used in this study is a composite laminate with four layers of randomly oriented short multidirectional glass fiber reinforced polyester matrix manufactured by the contact molding method. The molded plates are rectangular with dimensions of 600 × 300 mm2 with a mean thickness of 4 ± 0.5 mm and a volume fraction of 30% of glass fibers. Unsaturated polyester resin was employed as the matrix, and corresponding hardener, promoter, accelerator and initiator were used and included in the ingredients.
The manufacturing process is carried out in a plane mold, coated with a stripping agent and that has initially received a surfacing made up of a gel coat. The stratification by contact molding begins when the polymerization of the gel coat is considered to be sufficient. The operation consists in successively depositing glass E fibrous layers impregnated manually with polyester resin until obtaining the desired thickness, which is 4 mm on average. A roller is used to remove air bubbles. To get complete polymerization of the polyester resin, the plates are kept at room temperature of 20–25 °C and an average humidity of 50% in the open air for a few days. These environmental conditions, which are the average temperature and humidity along the coast of the Annaba region (east coast of Algeria) were maintained throughout the treatment.
After the period of resin hardening, the plates are withdrawn from the mold. Then they are cut into specimens using a diamond saw. Samples were divided into four groups corresponding to the different water immersion periods studied. Four time intervals were used, namely 0, 90, 180 and 270 days.
The reinforcement used is a surface mat of E glass of 350 g m−2 grammage with binder powder made up of short shopped fibers of length less than 40 mm and 10 µm diameter bound together by a binder.
It is well known that among the fiber reinforced materials glass fiber reinforced products (GFRP) are the cheapest and consequently have the greatest potential to be cost-effective. Their suitability for the production of complex-shaped components with reduced manufacturing times is widely proved, justifying their use in the reinforcement of products manufactured by UPS Chlef (Algeria) that are the subject of this study.
The principal physical and mechanical properties of the E glass fiber considered are supplied by the manufacturer (Vetrotex, Saint-Gobin, France) and are tensile strength of 2400 MPa, Young's modulus of 74 GPa, ultimate tensile strain of 3.5%, shear modulus of 30 GPa, Poisson's ratio of 0.25, density of 2.6 g m−3, approximately 15 µm diameter and 30 mm average length [28].
The chosen polyester resin has a 45 MPa tensile strength, 1.11 g cm−3 density at ambient temperature and 20 dPa s viscosity [28].
Specimens for the bending strength static tests and for the cyclic fatigue tests were in prismatic form of 80 mm length, 15 mm width and 4 mm thickness according to the EN ISO 14125 standard [29] or ASTM D-790 standard [30] as shown in Figure 1. Side surfaces were rectified and polished using a special grinding machine. The samples were immersed in a large bath containing natural seawater from Annaba beach (east coast of Algeria) and treated separately for 90, 180, and 270 days respectively. Specimens were withdrawn from the water on the designated days, wiped dry to remove the water on the surface and carefully dried with an absorbent paper until a constant weight was reached. The seawater was constantly renewed in order to conserve its biological activity.
The three-point bending static and cyclic tests were carried out using a Zwick/Roell Z 020 universal testing machine with a load cell of 20 KN and control software testXpert II allowing the acquisition and treatment of the data (Fig. 2). The distance between the two pivots was 64 mm and the load was applied at the middle of the sample until failure. Static tests were carried out with a constant cross-head speed of 2 mm min−1. Due to the variability of the mechanical characteristics of the composite materials, 12 samples were tested in the same conditions and the mean value of the data points obtained was taken as the measured result.
The cyclic fatigue tests were carried out under load control. The specimens subjected to cyclic fatigue were loaded and unloaded repeatedly with a sinusoidal waveform signal at different amplitudes correlated to the loading level, defined as a cyclic fatigue ratio rd of the minimum strength value to maximum strength value.
In this study a cyclic repeated solicitation was used corresponding to rd = σmin/σmax = 0 (Fig. 3). The loading frequency f was set to a minimum of 75 cycles min−1 corresponding to f = 1.25 Hz. The choice of the low frequency allows the avoidance of any side effects mainly due to the heating of the material.
The specimens were subjected to various loading levels used at 80%, 70%, 60%, 55%, 45%, 35% and 25% of the value of the static failure strength measured in three-point bending. For each value of rd a minimum of three specimens was tested. The tests were carried out at a room temperature of around 25 °C and an average relative humidity of 60–70%.
 |
Fig. 1 Specimens used in static and cyclic load. |
 |
Fig. 2 Universal testing machine used. |
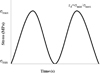 |
Fig. 3 Repeated sinusoidal waveform signal. |
3 Results and discussion
3.1 Weight gain rate
Weight gain is an important and significant parameter that characterizes the performance change of material in the whole degradation process, which includes the physical process and chemical process. The percent weight gain rate µ is calculated by the formula (1):
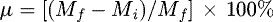 (1)
where Mi is the initial weight and Mf the weight of the specimen at each treated immersion time.
(1)
where Mi is the initial weight and Mf the weight of the specimen at each treated immersion time.
The weight of the samples before and after immersion in natural seawater was examined using an electronic analytical microbalance with a precision of 0.1 mg. It is acceptable to use µ to show some changes in the sample during the degradation process since all the samples used in the weight gain measurement have the same size. Weight gain was measured using all the fatigue samples.
Figure 4 illustrates the percent weight gain rate of the 4-layer laminate composite as a function of seawater soaking time. As seen, the change in the specimen's weight gain is apparent from the start of the seawater saturation and it increases quickly and sharply until 180 days, demonstrating the rapid moisture penetration into the materials. It is believed that a higher void content in the fiber-matrix interface will facilitate the entrance of humidity. After that, it does not change considerably and a weak weight loss of the specimen is observed relatively to the peak value due to extraction of soluble compounds.
It seems that the water uptake in a short period, as employed in this investigation, showed a gradual and monotonic increase of weight with increased immersion time during the six first days, as far as the composite is unsaturated, as illustrated in Figure 4.
One might imagine that at the beginning of the seawater immersion the water molecules would diffuse and penetrate rapidly into the volume of the material to occupy the numerous voids and cracks existing, which constitute ideal spaces to absorb the moisture [31]. This could lead to a large increase of the specimen's weight. It is believed that a higher porosity and void content in the matrix and in the fiber-matrix interface, as shown in the micrography of Figure 5, would facilitate this effect of the entrance of moisture, as has been signaled by Huang [32] in his study of the behavior of glass fiber/unsaturated polyester composites under a seawater environment. The micrography was taken by using a scanning electron microscope.
The samples immersed in seawater for a duration of 180 days show the largest increase of weight gain. It is clear that prolonged water immersion may finally make the sample saturated. It has been established that when the laminate composites have been immersed in water, the capillarity phenomenon will conduct the water molecules to the voids and cracks contained in the material. In this state, the water molecules will be attracted by the hydrophilic groups in the glass fiber and the unsaturated polyester.
By its nature, the water molecule has a strong tendency to form intermolecular hydrogen bonds in a polymeric material including the electronegative atoms (oxygen) as in the case of polyester resin. Its polarity supports the creation of agglomerates, compounds or clusters.
After 180 days of treatment in the seawater environment, hydrophilic groups of the polyester and the glass fiber will have chemical reactions with water molecules and soluble materials may be generated. Local small white spots and white particles oozed from the specimens, emerging principally at the edges and corners of the samples. This might be attributed to the extraction of soluble compounds as reported initially by Davies et al. [33] in their study of the influence of water absorption on the properties of glass/polypropylene composites, and by Fraga et al. [34] on the effect of water absorption on the dynamic mechanical properties of unsaturated polyester and vinyl ester glass fiber composites. This transformation will cause a gradual weight loss of the specimen and eventually the mass of the composite will drop below its original mass at mean term, which explains the reduction of the weight gain rate at 270 days as compared with that recorded at 180 days. This phenomenon has also been observed by Wei et al. [35,36] on glass-epoxy and basalt-epoxy composites immersed in artificial seawater and by Wang et al. [37] in a study of the chemical durability of a basalt-epoxy composite exposed to seawater. Therefore the behavior illustrated in Figure 4 is probably the consequence of these two effects: water absorption and extraction of soluble compounds.
It is worth noticing that, due to the capillary phenomenon, the water molecules present in the laminated composite material studied quickly occupy the compound interface between the glass fiber and the polyester resin. The fiber-matrix interface can undergo a deepening due to attacks and can be degraded by a hydrolysis reaction of the unsaturated groups in the polyester resin.
In addition, various studies have shown that if the hydrant generally increases the mass of the specimen, in other cases it is rather the opposite effect that appears, with a reduction in weight due to the destruction of the resin by a scrubbing phenomenon [2,6,38]. Also, the weight gain measurements in this study are somewhat higher than those obtained on glass fiber reinforced unsaturated polyester laminates treated in artificial seawater [2,31] or on epoxy resins reinforced respectively by basalt fibers and glass fibers treated with a seawater solution for different periods of time [35]. This difference can be explained by the different state of materials due to different manufacturing processes, the nature of the water, and the periods of immersion.
Universal graph processing software was employed to describe the simulated function of the variation of the weight gain rate in the case of this study. Figure 4 presents also the polynomial fit curve for the studied laminates. This polynomial adjustment of 2 degrees is given by the equation: y = −0.0002 x2 + 0.0673 x − 0.095 with a satisfactory coefficient of correlation of 0.987.
 |
Fig. 4 Percent weight gain rate of the 4-layer laminate composite versus seawater soaking time. |
 |
Fig. 5 Presence of numerous voids of various sizes and a higher porosity in the matrix and in the interfaces. |
3.2 Static flexural behavior
Figure 6 shows an example of the evolution of the typical load versus the displacement curve obtained from the three-point bending static tests and recorded on untreated specimens. The behavior is characterized by three distinct regions. In the first one, which is very short, the load increases linearly with the displacement until a specific level of strain is reached translating the elastic behavior of the material. This part is followed by an important nonlinear second phase with a registered staircase behavior which is related to the initiation and the evolution of the progressive damage that occurs in the laminate in the form of micro-cracking and disruption of the matrix; the weakest element of the composite, followed by debonding and fracture of the fiber-matrix interface, chunking, pull-out and fiber breakage and possible delamination. Increasing the load causes the development of micro-cracks and damage. Accumulation and growth of damage leads to the sudden fracture of the specimen. This brutal and total rupture occurs at the maximum load. Finally, a sudden load drop beyond the maximum load announces the unstable ruin of the specimen. It is interesting to note the knee point (joint) at which the two regions of the load-displacement curve have been observed and reported by several authors on SMC and on short fiber reinforced composite materials submitted to flexural or tensile static tests. The appearance of the knee point is generally related to the initiation of the first micro-cracks affecting the matrix.
The average values of the flexure mechanical properties measured in three-point bending and the corresponding standard deviations are:
-
Ultimate flexural strength: σst = 180 ± 25 MPa
-
Young's modulus: E = 5950 ± 869 MPa
These values are in agreement with that habitually reported in technical and scientific open literature and measured on similar composite materials [31].
These measured results always show a scatter in mechanical properties values, which is admitted now as a characteristic parameter of these laminated composites and can also be related to the heterogeneity of the microstructure and to the presence of defects like micro-porosities of different forms and dimensions randomly distributed in the volume, or to weakness of interfaces.
The order of magnitude of these dispersions is acceptable and returns in the usual ranges reported by the technical and scientifical literature for this kind of composite material [39–42]. It is to be announced that the dispersion in the values of the elastic module, which can be attributed to differences in state in the material (rate and orientation of fibers), is less important than that recorded on fracture stresses, which is influenced by the presence of defects, as already mentioned.
 |
Fig. 6 Example of stress-strain curve in three-point bending static test. |
3.3 Wöhler curves
A concern with using glass fiber composites in marine structures is the limited understanding and small database of information on their long-term durability and fatigue resistance in water. Generally, the stiffness degradation is one of the most widely used methods to monitor the fatigue damage propagation on composite materials. In this work, the focus is on the characterization of the laminates under cyclic three-point bending in terms of endurance or fatigue resistance. Therefore, to assume long-term durability, a fundamental understanding is essential in terms of strength resistance and material degradation under repetitive loading.
Wöhler diagrams are represented as plots of the maximum level applied fatigue strength versus the number of cycles Nr at failure for different loading levels in semi-logarithmic scale in Figures 7–10 for all the immersion times in natural seawater. A non-negligible scattering of the fatigue life values is observed. It is widely reported that there is large scatter in results from tests carried out to characterize the fatigue mechanical properties and the fatigue lifetime of composite materials.
Among the factors that most affect the dispersion in the fatigue lifetime results is the level of heterogeneity existing within the glass-polyester laminate samples. The dispersion can also be explained in terms of the previous existence of micro-cracks and micro-voids, porosity, the non-uniform effective volumetric fraction of reinforcement within the specimens, and diverse imperfections due to the manufacturing process.
Figures 7–10 show the results of fatigue tests described according to the linear equation of Wöhler: σfat = A−B · log Nr, where σfat and Nr are the applied maximum fatigue strength and the fracture number of cycles respectively. A and B are material constants linked to the material properties. According to several authors, A represents the static fracture strength of the specimen [43,44]. The term B quantifies the rate of change of the admissible loading by cycle decade.
The criterion adopted in this study is the complete fracture of the specimen. However, it should be noted that after 105 cycles, and for practical reasons in the laboratory, the test is stopped even if the specimen is not broken. We also consider that there is no fracture. The limit of endurance is therefore fixed at 105 cycles. The two coefficient values A and B are identified for each case of immersion in seawater by a straight linear regression performed on the experimental data. Table 1 summarizes the values of the coefficients A and B, the coefficients of correlation of linear regression R, the ratio B/A in absolute value, and therefore the static fracture strength σst of untreated specimens.
As shown in Table 1, the comparison between the values of coefficient A and σst for the untreated case shows a spread of 30% in favor of the coefficient A. This variation, which remains significant, can be explained by the important difference between the speed loading in these two types of solicitation and by the important dispersion of the fatigue test results. In addition, by comparing the slopes of the straight regression lines of the Wöhler curves (coefficient B in Table 1), it appears that they are very close and that the variations which separate them are not significant; the most important is 9%. This report indicates the negative effect of water on the resistance in the long term of glass-polyester composite materials. The increase of immersion time makes it possible for water to diffuse easily and to penetrate into the pores and the microscopic cracks of the matrix. This amplifies and accelerates the deterioration of the material structure and causes deterioration of the fiber-matrix interface, which is degraded in time, affecting gradually the performance of the material by an effect of progressive and diffuse damage.
It is believed that after a longer time in the seawater environment, water molecules will rapidly enter the interface of the composites between the fiber and the resin because of the capillarity [2]. Water can cause swelling and plasticization of the polyester resin and debonding at the glass-polyester matrix interface. During the moisture absorption of the interface, water molecules came into the free space of polymers or macrovoids formed by cavities and cracks, which induced more new cavities and cracks. Thus, debonding which may occur at the fiber-matrix interface [7] gradually damaged it seriously and thus the fibers can no longer be broken simultaneously. This implies that the bonding effect of the matrix on the fibers has been greatly reduced.
On the other hand, the polymer matrix and the fiber-matrix interface can be degraded gradually by a hydrolysis reaction of unsaturated groups within the resin [3–6], resulting in a weaker material with prolonged immersion time. The performance of the material is therefore seriously affected.
The groups of ester of polyester resin undergo hydrolysis reactions in a maritime environment, which support the extraction of the light styrene and glycol molecules of the composite in seawater. In the dissolved state, the NaCl present in the water would break apart into cations and anions. Ions would penetrate along with the water molecules into the composite. This situation causes damage to the matrix, fiber and interface. This leads to deterioration of the material, resulting in a decreased trend of the bending fatigue performance with prolonged immersion time for the same level of loading.
These are the main reasons for the physical damage of the laminates and the progressive deterioration of their fatigue resistance and endurance with prolonged treatment periods in natural seawater.
Therefore, despite the scatter in the fatigue tests, this progressive deterioration of the composite material creates a reduction of lifetime with the increase of seawater immersion time for a considered loading level.
Figure 11, which presents the four Wöhler curves corresponding to the four environments, illustrates this behavior. These curves, which show very close slopes, are thus approximately parallel.
This representation shows clearly that for the same level of loading the lifetime of the composite material decreases with the increase of the immersion time in seawater, indicating that the material has experienced some form of physical damage and irreversible chemical degradation.
The phenomenon of diffusion/infiltration may cause the matrix to swell and break, leading to irreversible degradation that is amplified with time, affecting seriously the lifetime of these materials when submitted to cyclic loading.
It is clear that the diffusion of sodium chloride molecules (chloride ions) around the composite toward the inside of the material is the main form of corrosion damage to the matrix material. The hydrolysis reaction which occurred in the composite, including the hydrolysis of fiber, matrix, and their interface, may break the molecular chain and reduce the curing degree of the cross-linked network, resulting in the changes of material performance. It may be claimed that extraction of the soluble material at the interface may damage the coherence between the matrix and the fiber.
In addition, it seems that the oxide of alkaline metal in glass fiber would reduce its chemical stability. Thus the fiber can more easily react with other ions. This causes the deterioration of the glass fiber, the matrix and the interface, affecting the lifetime of these materials, involving a reduction in the fatigue strength for long-term immersion. All these effects degrade the initial properties of the composite even before even it starts to undergo loading.
The overall behavior and performance of a composite material such as glass/polyester cannot be explained only in terms of specific properties of the components, but the interface/interphase between the fibers and the matrix is of great importance as it has been reported by Kuttner et al. [45] on a recent study on the influence of the polymeric interphase design on the interfacial properties of fiber-reinforced composites. The water penetrates the interface in the composite during aging can modify the interfacial adhesion nature of the system which causes a degradation of the mechanical performance of the glass/polyester composite. After longer time seawater immersion one should notice that moisture damage begins near the surface of the material and spreads inward over time, with cracks tending to grow parallel to the free surface [46].
It thus remains essential to know as a preliminary the kinetics of absorption which govern the kinetics of degradation in these materials to be able to include/understand and envisage their behavior. The presence of water involves reversible and irreversible structural degradations [7,47,48].
The noticed decreasing trend of the fatigue lifetime with increased immersion time can be well illustrated in Figure 12 for different levels of loading.
The seawater causes a negative effect on the fatigue behavior of glass-polyester laminates. Increasing immersion time allows the seawater to diffuse and to penetrate into the structure of the material. This alters the resin and the fiber-matrix interface, reducing the effect of the bonds and progressively affecting the performance of the material by a progressive and diffuse damage which increases with the increase of loading level.
 |
Fig. 7 Wöhler curve in dry environment. |
 |
Fig. 8 Wöhler curve after 90 days of immersion in seawater. |
 |
Fig. 9 Wöhler curve after 180 days of immersion in seawater. |
 |
Fig. 10 Wöhler curve after 270 days of immersion in seawater. |
Values A and B of coefficients of Wöhler curves.
 |
Fig. 11 Idealized Wöhler curves for the 4 environments. |
 |
Fig. 12 Trend of fatigue lifetime versus immersion time for different levels of loading. |
3.4 Causes of the dispersion
The slightly low values of the coefficients of linear correlation for the Wöhler curves indicate that the important dispersion observed over the lifetime is mainly related to the heterogeneous nature of the composites and to the nature of the test specimens, which seldom have comparable characteristics. Indeed, the volume fraction, the length and orientation of the fibers, the density and the defects distribution as well as the physical and mechanical characteristics differ from one test specimen to another and from one region to another of the same specimen. Thus, all the events preceding fracture in fatigue depend on a series of random processes whose conjugation results in an important dispersion in the lifetime results between test specimens subjected to the same loading level and under the same conditions. Thus, it appears clearly that in addition to the natural dispersion of the material, the fatigue behavior has allowed clean dispersion, like a physical fact of the fatigue phenomenon. The state of damage in fatigue is in general characterized by a combination of density and fibers orientation and microscopic cracks which seem to be affected by the loading as well as the states of conditioning of the test specimen. The accumulation and the evolution of this damage in the case of the studied composites is due mainly to matrix micro-cracking mechanisms, interfacial delamination, debonding, pull-out and fracture of fibers, which confer on the composite variable the kinetics of damage conditioned by its microstructure and loading type. Many studies report that the evolution stages of damage in cases of cyclic loading have the same nature as those encountered in static loading, but with different chronology and different amplitude. The deterioration of the composites takes place during the first cycles of fatigue loading, after which the density of damage increases gradually until the final fracture. In addition, total failure no longer seems to be a single concept to be adopted like a qualitative description of fracture criteria. The use of acoustic emission techniques coupled with those of microscopic video monitoring could yield better information about the main mechanisms of damage in fatigue, leading to more descriptive criteria of fracture and a reduction in the dispersion of the results from these materials.
3.5 Normalized Wöhler curves
The normalized Wöhler curves for all the studied environments are illustrated in Figure 13. This form of representation makes it possible to highlight the quantified degradation rate by the slope (B/A) in the absolute value of the Wöhler equation. This rate is constant per decade of cycles for each period of seawater immersion. Its values are also gathered in Table 1 for all the immersion times tested.
This rate of degradation increases with the increase in the immersion time in seawater. Figure 14 illustrates this behavior. This evolution seems to obey a linear law which is given by the equation of the following linear straight regression line: y = ax + b, with an excellent coefficient of correlation equal to 0.99.
This concept of the degradation rate per decade of cycles has been raised and reported by many authors based on randomly oriented short fiber reinforced composite materials. They estimate it in general at 10% [44–50]. However, no explanation has been advanced to characterize this constant value. Roy et al. [51], in fatigue testing a series of laminated composite materials based on mat glass fiber reinforced polyester matrix in joint adhesive bonded composite-composite and composite-steel for marine applications report rates of 13% (0°), 7% (45°), 9% (composite-composite) and 10% (steel-composite). They conclude that given the scatter in properties, the 10% loss per decade from the fiber data will give a reasonable indication of the fatigue effects for these materials. However, Harris [52] has pointed out the unlikelihood of a single mechanistic model being applicable when both matrix and fibers contribute to the damage.
 |
Fig. 13 Standardized Wöhler curves. |
 |
Fig. 14 Variation of degradation rate according to the immersion time in seawater. |
3.6 Other forms of representation
It has been reported in scientific literature that the problem of dispersal of fatigue lifetime results is the consequence of the structural heterogeneity of the defects since the elaboration of material [53]. Since these defects present in the material are difficult to measure, it is advisable to use as a random variable, for a given stress level, the number of cycles to failure to explain the existence of defects by a probabilistic approach. N. Ngarmaïm et al. [54] have formulate a probabilistic model of a new expression of the SN curve in fatigue based on the concept of “weakest link” of Weibull introducing a new parameter Nc, the number characteristic of cycles corresponding to the failure probability equal to 1. His confrontation with the terms of the curve most used SN, particular those Basquin, the Wöhler and the Stromeyer, the fatigue tests and martensite steels P22O 100C6 data provided errors of about 5% maximum for models Basquin,Wöhler and that proposed.
Among the various models of results representation in fatigue tests synthesized in the literature, those whose coefficients are easy to identify starting from the experiment were tested against the Wöhler curve. Thus, in order to give an account of an asymptotic branch for large cycle numbers, Basquin [55] has proposed: σmax = σf (2Nr)α. σmax and Nr respectively represent the maximum stress of the considered cycle and the cycle number at fracture. σf and α. are constants of material and respectively represent the stress coefficient in fatigue and the Basquin exhibitor.
Hwang and Han [56] propose: Nr = [C (1 − r)]1/c where C and c are constants of material and r the stress applied level, equal to σmax/σst.
The layouts of ln (σmax) according to ln (2Nr) for the Basquin equation and log (1−r) according to log (Nr) for that of Hwang and Han are lines whose coefficients make it possible to identify the constants for each equation. These values are gathered in Table 2 with the correlation coefficients R of each line.
Figure 15 shows the layout of these two models together with that of Wöhler's equation around the experimental points in the case of the dry environment.
The statements appear thus. In olygocyclic field fatigue, the experimental points are described better by the Hwang and Han equation. In higher endurance fields of more than 105 cycles, the Basquin equation, which seems to have a curve tending towards an asymptote, allows us to determine an endurance limit. However, given the important dispersion experimental points, it appears that the Wöhler curve has the advantage of simplicity and although it cannot give an account of a horizontal branch, it does give the average part an often good representation. It can be used for comparisons of variation in the layout of the endurance curves corresponding to variations of the materials composition, test frequency, environment, loading amplitude, etc.
Values of Basquin and Hwang & Han coefficients equations.
 |
Fig. 15 Various representations of σmax according to log Nr. |
4 Identification of damage and failure mechanisms
The behavior is elasto-damageable. The damage is diffuse and develops continuously until the final failure. The phenomena which cause this damage are many and complex and remain difficult to identify and to quantify. Nevertheless, those dominating are the cracking of the matrix, the delamination and fracture of the matrix-fiber interface, the debonding of fibers and to a lesser degree, pull-out and fracture of fibers. It was also noticed that the evolution of fatigue damage depends on the loading amplitude. The deterioration of the composites in fatigue takes place as in the static case from the first cycles of loading and increases gradually until the total failure. It is reported that the presence of mat layers in composites used for marine structures leads to the initiation of damage at low strain levels typically around 0, 1% [19]. According to many studies, this state is characterized by three stages of progressive evolution. A first stage corresponds to the initiation of micro-damage resulting in a fast fall in the standardized elasticity modulus. A second stage shows less important kinetics of lasting damage in which the micro-damage gradually develops and there is an increase of density. The last stage is characterized by a sharp decline of the rigidity, which results in the appearance of macroscopic cracks causing the total fracture of material. This complexity of the rupture and damage mechanisms make it complex and difficult both to model the behavior and to forecast the fatigue lifetime [5].
It is clear that a particular structure can thus exhibit one or more of these damage modes, which complicates the prediction of the dominant causes of fractures.
Generally, the fatigue damage state of composite materials is characterized by a combination of the density and orientation of micro-cracks, whose initiation and evolution seem to be affected by the level and the amplitude of loading and the packaging conditions of the test pieces. This damage in the case of the studied laminates is mainly due to the micro-cracking mechanisms of the matrix, matrix interfacial debonding, fracture of fibers, and pull-out. The accumulation and development of these progressive degradation mechanisms provide the material kinetics of damage, which can be conditioned by its microstructure and the type of load, and these can also be identified from the experimental results. According to Benabdi et al. [10], it appears that the stages of evolution of the damage in the case of cyclic loading on composite plate of carbon-epoxy have the same nature as those encountered in static loading. The composites deterioration occurs in the early fatigue loading cycles and increases gradually until the final fracture. It is characterized by three stages of progressive evolution.
5 Conclusion
The investigation on the quasi static and fatigue three-point loading behavior of randomly oriented glass fiber reinforced polyester laminated composite materials immersed in different seawater environments shows the following salient points:
-
The weight gain change of the randomly oriented glass fiber reinforced polyester laminated composite materials after being immersed in a natural seawater environment is a result of the joint action of the absorption of water, which is predominant at the initial stage and is caused by diffusion/infiltration phenomena, and the extraction of soluble compounds, which may play a major role at the later stage and is caused by hydrophilic groups of the polyester and the glass fiber having chemical reactions with water molecules.
-
The mass change of glass-polyester composite after having undergone immersion in seawater is a combination of two effects: the water absorption and the extraction of soluble matter. At the initial stage, the water absorption is prevalent, which generates an increase in the mass, and at the later stage, after a treatment exceeding 6 months in seawater, the extraction of soluble matters plays an important role.
-
The fatigue results present an important dispersion characteristic of these composite materials in cyclic loading. The Wöhler curves modeled by linear straight regression lines give the average part a rather good representation.
-
The damage which is initiated in fatigue for these materials is diffuse and its mechanisms, which are numerous, develop by the debonding mechanism and bridging of cracks, by matrix micro-cracking and fiber fracture, and by fiber-matrix delamination. The complexity of this fracturing and the damage mechanisms make it complex to model this behavior or to forecast the fatigue lifetime with good precision.
-
The glass-polyester composite materials are characterized by a constant degradation rate during their lifetime. This rate seems to increase with the increase of immersion time at a constant speed.
Nomenclature
Mf: weight of the specimen at each treated immersion time, g
Mi: initial weight before immersion in water, g
r: stress applied level in Hwang and Han equation
rd: stress ratio in fatigue test
µ: percent weight gain rate, %
σf: stress coefficient in fatigue
σfat: applied maximum fatigue strength, MPa
σmax: maximum stress in fatigue test, MPa
σmin: minimum stress in fatigue test, MPa
σst: ultimate static flexural strength of untreated specimens, MPa
Acknowledgments
The authors thank the management of the UPS unit Chlef (Algeria) for its assistance with the manufacturing, initial packaging and sending of the laminated plates and Mr Yves Grohens from UFR SSI of ≪Université Bretagne Sud-Lorient (France)≫ for his encouragements and his goodwill to co-operate.
References
- G.Z. Liu, D.H. Li, L.G. Huang, D.X. Zhang, Experiments on corrosion mechanism and performance evolution rule of GFRP in salt steam environment, FRP/CM 1 (2008) 35–40 [Google Scholar]
- G. Huang, S. Hong Xia, Effect of water absorption on the mechanical properties of glass-polyester composites, Mater. Des. 28 (2007) 1647–1650 [CrossRef] [Google Scholar]
- S. Pavlidou, C.D. Papaspyrides, The effect of hygrothermal history on water absorption and interlaminar shear strength of glass-polyester composites with different interfacial strength, Compos. A 34 (2003) 1117–1124 [CrossRef] [Google Scholar]
- K. Takafumi, R.A. Pearson, The moisture effect on the fatigue crack of glass particle and fiber reinforced epoxies with strong and weak bending conditions part 2: a microscopic study on toughening mechanism, Compos. Sci. Technol. 64 (2004) 1991–2007 [CrossRef] [Google Scholar]
- J. Zhang, M. Zhang, Visual experiments for water absorbing process of fibre-reinforced composites, J. Compos. Mater. 38 (2004) 779–790 [CrossRef] [Google Scholar]
- A. Kootsooks, A.P. Mouritz, Seawater durability of glass and carbon polymer composites, Compos. Sci. Technol. 64 (2004) 1503–1511 [CrossRef] [Google Scholar]
- V.A. Alvarez, A. Vazquez, Effect of water absorption on the flexural properties of fully biodegradable composites, J. Compos. Mater. 38 (2004) 1165–1181 [CrossRef] [Google Scholar]
- I. Krystyna, G. Laurent, The effect of water immersion ageing on low-velocity impact behaviour of woven aramid-glass fibre/epoxy composites, Compos. Sci. Technol. 64 (2004) 2271–228 [CrossRef] [Google Scholar]
- E.P. Gellert, D.M. Turley, Seawater immersion ageing of glass-fibre reinforced polymer laminates for marine applications, Composites 30 (1999) 1259–1265 [CrossRef] [Google Scholar]
- Y. Shan, K. Liao, Environmental fatigue of unidirectional glass-carbon fiber reinforced hybrid composite, Compos. B: Eng. 32 (2001) 355–363 [CrossRef] [Google Scholar]
- T.K. Tsotsis, S. Keller, K. Lee, J. Bardisc, J. Bishd, Aging of polymeric composite specimens for 5000 hat elevated pressure and temperature, Compos. Sci. Technol. 61 (2001) 75–86 [CrossRef] [Google Scholar]
- S. Marais, M. Metayer, T.Q. Nguyen, M. Labbe, J.M. Saiter, Diffusion and permeation of water through unsaturated polyester resins − influence of resin curing, Eur. Polymer J. 36 (2000) 453–462 [CrossRef] [Google Scholar]
- L.H. Strait, M.L. Karasek, M.F. Amateau, Effects of seawater immersion on impact resistance of glass fibre reinforced epoxy composites, J. Compos. Mater. 26 (1992) 2118–2133 [CrossRef] [Google Scholar]
- L. Gautier, B. Mortaigne, V. Bellenger, J. Verdu, Osmotic cracking in unsatured polyester matrices under humid environment, J. Appl. Polym. Sci. 79 (2001) 2517–2526 [CrossRef] [Google Scholar]
- A.P. Mouritz, J. Gallagher, A.A. Goodwin, Flexural strength and interlaminar shear strength of stitched GRP laminates following repeated impacts, Compos. Sci. Technol. 57 (1997) 509–522 [CrossRef] [Google Scholar]
- E. Wu, K. Shyu, Response of composite laminates to contact loads and relationship to low-velocity impact, J. Compos. Mater. 27 (1993) 1443–1464 [CrossRef] [Google Scholar]
- M.S. Found, I.C. Howard, Single and multiple impact behavior of a CFRP laminate, Compos. Struct. 32 (1995) 159–163 [CrossRef] [Google Scholar]
- D. Ray, B.K. Sarkar, N.R. Bose, Impact fatigue of glass fibre-vinylester resin composites, Compos. A: Appl. Sci. Manuf. 32 (2001) 871–876 [CrossRef] [Google Scholar]
- D. Ray, B.K. Sarkar, N.R. Bose, Impact fatigue behaviour of vinylester resin matrix composites reinforced with alkali treated jute fibres, Compos. A: Appl. Sci Manuf. 33 (2002) 233–241 [CrossRef] [Google Scholar]
- K. Takafumi K, R.A. Pearson, The moisture effect on the fatigue crack of glass particle and fibre reinforced epoxies with strong and weak bending conditions part 2. A microscopic study on toughening mechanism, Compos. Sci. Technol. 64 (2004) 1991–2007 [CrossRef] [Google Scholar]
- A. El Mahi, A. Bezzazi, Describing the flexural behaviour of cross-ply lamonates under cyclic fatigue, Appl. Compos. Mater. 16 (2009) 33–53 [CrossRef] [Google Scholar]
- K. Kanny, H. Mahfuz, Flexural fatigue characteristics of sandwich structures at different loading frequencies, Compos. Struct. 67 (2005) 403–410 [CrossRef] [Google Scholar]
- G. Belingardi, P. Martella, L. Perom, Fatigue analysis of honeycolb composite sandwich beams, Compos. A: Appl. Sci. Manuf. 38 (2007) 1183–1191 [Google Scholar]
- Y.M. Jen, H.B. Lin, Temperature-dependent monotonic and fatigue bending strengths of adhesively bonded aluminium honeycomb sandwich beams, Mater Design 45 (2013) 393–406 [CrossRef] [Google Scholar]
- M.Z. Hassan, Z.W. Guan, W.J. Cantwell, G.S. Langdin, G.N. Nurick, The influence of core density on the blast resistance of foam-based sandwich structures, Int. J. Impact Eng. 50 (2012) 9–16 [CrossRef] [Google Scholar]
- Y.M. Jen, L.Y. Chang, Effect of thickness of face sheet on the bending fatigue strength of aluminum honeycomb sandwich beams, Eng. Fail. Anal. 30 (2009) 1282–1293 [CrossRef] [Google Scholar]
- W. Boukharouba, A. Bezzazi, F. Scarpa, Identification and prediction of cyclic fatigue behaviour in sandwich panels, Measurement 54 (2014) 161–170 [CrossRef] [Google Scholar]
- G. Mirouzi, B. Redjel, D. Rangeard, B. Kebaili, Influence of E short glass fiber and glass texture reinforcement mode and rate on the mechanical performances of resin concretes, J. Mater. Environ. Sci. 7 (5) (2016) 1759–1772 [Google Scholar]
- P. Krawczak, Essais des plastiques renforcés Techniques de l'Ingénieur, traité plastiques et composites (1997) AM5405 1–26 [Google Scholar]
- ASTM D-790-81, Flexural properties of unreinforced and reinforced plastics and electrical insulation, Annual Book of ASTM Standard (2007) 403–405 [Google Scholar]
- A. Apicella, C. Migliaresi, L. Nicolais, S. Roccotelli, The water aging of unsaturated polyester-based composites: influence of resin chemical structure, Composites 14 (1983) 387–392 [CrossRef] [Google Scholar]
- G. Huang, Behaviors of glass fiber/unsaturated polyester composites under sea water environment, Mater. Des. 30 (2009) 1337–1340 [CrossRef] [Google Scholar]
- P. Davies, F. Pomies, L.A. Carlssion, Influence of water absorption on transverse tensile properties and shear fracture toughness of glass/polypropylene, J. Compos. Mater. (1996) 30 1004–1019 [CrossRef] [Google Scholar]
- A.N. Fraga, V.A. Alvarez, O. De la Osa, A. Vazquez, Relationship between dynamical mechanical properties and water absorption of unsaturated polyester and vinyl ester glass fiber composites, J. Compos. Mater. 37 (2003) 1553–1574 [CrossRef] [Google Scholar]
- B. Wei, H. Cao, S. Song, Degradation of basalt fibre and glass fibre/epoxy resin composites in seawater, Corros. Sci. 53 (2011) 426–431 [CrossRef] [Google Scholar]
- B. Wei, H.L. Cao, S.H. Song, Environmental resistance and mechanical performance of basalt and glass fibers, Mater. Sci. Eng. A 527 (2010) 4708–4715 [Google Scholar]
- M.C. Wang, Z.G. Zhang, Y.B. Li, M. Li, Z.J. Sun, Chemical durability and mechanical properties of alkali-proof basalt fiber and its reinforced epoxy composites, J. Reinf. Plast. Compos. 27 (2008) 393–407 [Google Scholar]
- C. Suri, H. Hamada, K. Koyama, Blister appearance in thermoplastic composites, Adv. Compos. Mater. 10 (2001) 63–75 [CrossRef] [Google Scholar]
- H.N. Dhakal, Z.Y. Zhang, M.O.W. Richardson, Effect of water absorption on the mechanical properties of hemp fibre reinforced unsaturated polyester composites, Compos. Sci. Technol. 67 (2007) 1674–1683 [Google Scholar]
- D.E. Mouzakis, H. Zoga, C. Galiotis, Accelerated environmental ageing study of polyester/glass fiber reinforced composites (GFRPCs), Compos. B 39 (2008) 467–475 [CrossRef] [Google Scholar]
- Y. Menail, A. El Mahi, M. Assarar, B. Redjel, A. Kondratas, The effects of water aging on the mechanical properties of glass-fiber and kevlar-epoxy composite materials, Mechan., Nr2 57 (2009) 8–13 [Google Scholar]
- C. Alves, A.P.S. Dias, A.C. Diogo, P.M.C. Ferrao, S.M. Luz, A.J. Silva, L. Reis, M. Freitas Eco-composite: the effects of the jute fiber treatments on the mechanical and environmental performance of the composite materials, J. Compos. Mater. 45 (5) (2011) 573–589 [CrossRef] [Google Scholar]
- J.F. Mandell, D.D. Huang, F.J. Mc Garry, in: B.A. Sanders (ed.), Short Fiber Reinforced Composite Materials ASTM STP 772 (1982) 3–32 [CrossRef] [Google Scholar]
- B. Redjel, Fatigue damage in short fiber reinforced composite materials, in: S. Degallaix, C. Bathias, R. Fougères (eds.), 8th International conference on fatigue of composites, SF2M, Eighth international spring meeting, Paris, France, 1997, pp. 165–172 [Google Scholar]
- C. Kuttner, A. Hanisch, A. Schmalz, H. Eder, M.H. Schlaad, I. Burgert, A. Fery, Influence of the polymeric interphase design on the interfacial properties of fiber-reinforced composites, Appl. Mater. Interfaces 5 (2013) 2469–2478 [CrossRef] [Google Scholar]
- S. Sanghamitra, C.R. Bankim, Environmental effects on fibre reinforced polymeric composites: evolving reasons and remarks on interfacial strength and stability, Adv. Colloid Interface Sci. 217 (2015) 43–67 [CrossRef] [PubMed] [Google Scholar]
- Y. Menail, A. El Mahi, B. Redjel, M. Assarar, Vieillissement en eau de mer d'un matériau composite Kevlar époxyde, J. Mater. Process. Environ. 2 (2014) 59–66 [Google Scholar]
- Y. Menail, A. El Mahi, M. Assarar, B. Redjel, Acoustic emission monitoring of damage mechanisms an aramid-epoxy composite after tensile fatigue and aging seawater, Mechanics 22 (2016) 14–18 [CrossRef] [Google Scholar]
- J.F. Mandell, F.J. Mc Garry, D.D. Huang, C.G. Li, Some effects of matrix and interface properties on their fatigue of short fiber reinforced thermoplastics, Polymer Compos. 4 (1983) 32–39 [CrossRef] [Google Scholar]
- D. Vigneron, mécanique de renforcement et mécanismes de rupture dans les polyamides renforcés par fibres courtes, Thèse de Doctorat, Université de Technologie de Compiègne (UTC), France, 1983 [Google Scholar]
- A. Roy, J. Royer, P. Davies, Fatigue behavior of marine composites: from specimen to structures, in: S. Degallaix, C. Bathias, R. Fougères (Eds.), 8th international conference on fatigue of composites, SF2M, eighth international spring meeting, Paris, France, 1997, pp. 165–172 [Google Scholar]
- B. Harris, Fatigue behaviour of polymer based composites, in: A.H. Cardan (Ed.), Durability analysis of composite structural systems, Balkema, 1996, pp. [Google Scholar]
- M.G. Dominguez-Almaraz, Prediction of very high cycle fatigue failure for high strength steels based on the inclusion geometrical properties, Mech. Mater. 40 (2008) 636–640 [CrossRef] [Google Scholar]
- N. Ngarmaïm, B. Tikri, B. Bassa, N. Kimtangar, F. Pennec, J.-L. Robert, A new expression of the curve S-N in fatigue based on the concept of the “weakest link” of weibull, Global J. Res. Eng.: Mech. Mech. Eng. 14 (2014) 21–26 [Google Scholar]
- C. Bathias, J.P. Baillon, La fatigue des matériaux et des structures Collection UTC, (Ed.) SA Maloine, Paris, France, 1980 [Google Scholar]
- H. Hwang, K.S. Han, Fatigue of composites-fatigue modulus concept and life prediction, J. Compos. Mater. 20 (1986) 154–165 [CrossRef] [Google Scholar]
Cite this article as: D. Djeghader, B. Redjel, Fatigue resistance of randomly oriented short glass fiber reinforced polyester composite materials immersed in seawater environment, Mechanics & Industry 18, 604 (2017)
All Tables
All Figures
 |
Fig. 1 Specimens used in static and cyclic load. |
| In the text | |
 |
Fig. 2 Universal testing machine used. |
| In the text | |
 |
Fig. 3 Repeated sinusoidal waveform signal. |
| In the text | |
 |
Fig. 4 Percent weight gain rate of the 4-layer laminate composite versus seawater soaking time. |
| In the text | |
 |
Fig. 5 Presence of numerous voids of various sizes and a higher porosity in the matrix and in the interfaces. |
| In the text | |
 |
Fig. 6 Example of stress-strain curve in three-point bending static test. |
| In the text | |
 |
Fig. 7 Wöhler curve in dry environment. |
| In the text | |
 |
Fig. 8 Wöhler curve after 90 days of immersion in seawater. |
| In the text | |
 |
Fig. 9 Wöhler curve after 180 days of immersion in seawater. |
| In the text | |
 |
Fig. 10 Wöhler curve after 270 days of immersion in seawater. |
| In the text | |
 |
Fig. 11 Idealized Wöhler curves for the 4 environments. |
| In the text | |
 |
Fig. 12 Trend of fatigue lifetime versus immersion time for different levels of loading. |
| In the text | |
 |
Fig. 13 Standardized Wöhler curves. |
| In the text | |
 |
Fig. 14 Variation of degradation rate according to the immersion time in seawater. |
| In the text | |
 |
Fig. 15 Various representations of σmax according to log Nr. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


