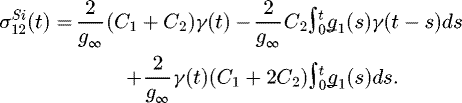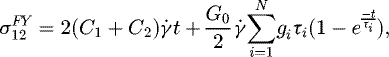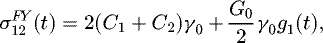| Issue |
Mechanics & Industry
Volume 19, Number 5, 2018
|
|
|---|---|---|
| Article Number | 502 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/meca/2018014 | |
| Published online | 14 December 2018 | |
Regular Article
The capability of three seperable finite-strain viscoelastic models to predict response of a filled rubber material
1
Université de Tunis El Manar, Ecole Nationale d'Ingénieurs de Tunis, Laboratoire de Mécanique Appliquée et Ingénierie LR-11-ES19 (LRMAI), BP 37 Le Belvédère, 1002 Tunis, Tunisie
2
Ecole Centrale de Lyon, Laboratoire de Tribologie et Dynamique des Systèmes (LTDS) CNRS: UMR5513,
36 Avenue Guy de Collongue, 69130 Ecully, France
* e-mail: jridinidhal@gmail.com
Received:
7
July
2016
Accepted:
10
February
2018
Three integral-based finite strain viscoelastic models under the assumption of time-strain separability have been investigated within this work. To this end, experimental investigation has been conducted on a carbon black filled rubber, a mixture of natural rubber and bromobutyl. The monotonic tests were performed to capture the long-term response of the material. Relaxation tests were intented to identify the time-dependent material properties, and completed with a dynamic mechanical analysis. Models under consideration are Christensen, Fosdick and Yu and Simo model implemented in the finite element solver Abaqus. Under the assumption of an homegeneous incompressible material with a Mooney-Rivlin elastic potential, the response of the three models is compared for uniaxial tension and simple shear motions in time and frequency domains with respect to strain-rate, frequency and static predeformation dependencies. The equilibrium and non-equilibrium stress is predicted in a limited range mainly related to the choice and identification of the hyperelastic model. For stress relaxation, the long-term response is asymptotically reached with good accuracy, while the hysteritic response is mainly overestimated for Christensen model, and better approximated for both Fosdick and Yu and Simo models. In the frequency domain, Fosdick and Yu model shows no dependence on the predeformation. Christensen model is likely adapted to unfilled rubbers, and is unable to predict the softening effect due to the static predeformation effect. Simo model shows better prediction capabilities with a minimal set of material parameters.
Key words: Rubber vulcanizate / experimental characterization / finite strain viscoelasticity / time-strain separability / dynamic material properties
© AFM, EDP Sciences 2018
1 Introduction
Rubber compounds are widely used as damping components for their dissipative properties and their ability to undergo severe loading conditions. The load case of large static predeformation superimposed by small amplitude dynamic excitation is commonly used for industrial applications. Since the constitutive behavior of rubber materials is highly non-linear in static and dynamic regimes [1,2], it is of major importance to measure the sensitivity of the dynamic response to the influencing parameters, and be able to predict the impact of those effects on the products.
To model the mechanical behavior of elastomeric materials, many methods based on elasticity [3,4] or viscoelasticity [5–8] have been developed. Two different approaches can be found in literature to model the large strain-rate dependent response of viscoelastic materials [9]. The first approach is founded on an extension of the Boltzmann superposition principle to finite strain [10]. The total stress is the sum of a long-term equilibrium response and a viscoelastic overstress expressed in term of time convolution integrals. The second approach consists on decomposition of deformation gradient into elastic and inelastic parts [11]. The elastic part derives from an hyperelasticity model while the viscoelastic overstressed part is related to the so-called internal strain, determined by an evolution equation [12,13]. To afford theoretical simplicity, the time-strain separability or factorability assumption [14,15], based on experimental observations of stress relaxation, is frequently introduced in the formulation of finite strain viscoelasticity constitutive models.
In this paper, we examine the response of three heriditary integral-based constitutive models for uniaxial tension and simple shear motions in time and frequency domains, under the separability assumption. It is to note that Ciambella et al. [16] have proposed a comparison of some integral-based viscoelastic models in time domain. The present paper is organised as follows. In Section 2 we discuss experimental investigation conducted to identify the material parameters. The sensitivity of the response to strain-rate effect was investigated through monotonic tests. Multistep tests were performed to capture the long-term response of the material. Relaxation tests were intended to identify kernel function modeling the material memory effect. This experimental investigation were completed by a dynamic mechanical analysis, aiming to be compared to models responses with respect to frequency and predeformation dependence effects. Section 3 is dedicated to the finite strain viscoelastic models analysis. We present the the constitutive relations which are included in this study. The considered models are a single integral hereditary model under the incompressibility constraint: Christensen [17], Fosdick and Yu [18] and Simo model [19]. In the same section, the three-dimensional constitutive equations introduced are reduced to a one-dimension stress–strain relations for uniaxial tension and shear loading paths. The response for several loading paths are then determined. In the frequency domain, the complex shear modulus is determined as described in [17] and [20]. Finally, Section 4 reports the obtained comparison results issued from constitutive equations and experimental observations, resuming the predictive capabilities of the considered models.
2 Experimental set-up
2.1 Experimental procedure
The vulcanized rubber material investigated throughout this work is NR/BIIR, a mixture of natural rubber known for being stiff and bromobutyl rubber used for its particular damping capacity.
Taking different loading paths into account, sets of experiments including uniaxial tension and simple shear tests were carried out on an Instron 3345 tensile machine. The tension tests were performed using standardized Haltere type 2 specimens. Shear tests were achieved with the use of quad-shear specimens holders [21]. The monotonic experiments were performed at room temperature under displacement-control, and the engineering strain was calculated assuming an homogeneous deformations on the whole specimen. At least three tests were carried out for each loading path. carried out for each loading path. For the uniaxial tension, the specimens were loaded till 500% of deformation at different strain-rates of 10%/min, 100%/min and 200%/min. Avoiding that the shear occurs on glue, the shear tests were loaded till 100% of deformation at 5%/min, 10%/min and 20%/min. Focusing on the equilibrium stress response, we make use of multistep experiments at different strains with holding periods of 10 min. during which the applied strain was held constant [22].
To identify the time-dependent viscoelastic behavior, stress relaxation experiments were conducted on a Metravib DMA machine of load capacity 50N by mean of the double shear specimens holder. The experimental procedure consists on deforming the specimen at different strains levels, ranging from 10 to 50%, and holding the assembly for four hours. An hysteresis is seen to quickly vanish and the steady relaxation response is measured.
Investigating the dynamic properties of the considered elastomers, the experimental procedure consists on superimposing a simple shear predeformation and a sinusoidal strain after sufficient relaxation time of about 10 mn.
To consider the frequency-dependence of the materials behavior, frequency sweep tests with stepwise changing frequency from 0.1 up to 30 Hz at different predeformation levels from 10 up to 30% to measure the sensitivity of the dynamic response to the service point.
2.2 Experimental results
The available experimental data obtained from quasi-static and dynamic tests were used as database to identify and compare the response of the considered models below. Figure 1 shows the pronounced strain rate dependence on the material: we observed evolution of the engineering stress with increasing strain velocity till a pure elastic response. The technique described in [23] was used to identify the time-independent equilibrium hyperelastic response, graphically shown in Figure 2.
Relaxation tests were intended to determine the relaxation kernel, including large characteristic times. Observations in Figures 3 and 4 confirm the separability assumption: the phenomenological behavior of the considered material is only time dependent none deformation dependent [2,24,25].
These results are completed with the dynamic properties investigation, evaluated in term of storage shear modulus and loss factor. For the investigated frequency range, both shear storage modulus and loss factor exhibit the same frequency-dependent behavior: the material stiffens with increasing frequency, as shows Figures 5 and 6. Since rubber compounds are commonly used at a predeformed configuration, we made interest in the static predeformation effect on dynamic properties. Figures 5 and 6 shows that increasing predeformation leads to a softening of the material. It is to note that the dynamic deformation amplitude was set as maximum dynamic strain is less than 1%, in order to avoid a dynamically softening effect, the so-called Payne-effect [26,27].
 |
Fig. 1 Non-equilibrium stress response at different strain-rates. |
 |
Fig. 2 Time independent equilibrium stress–strain curve. |
 |
Fig. 3 Relaxation spectrum at different deformation levels: quasi-linear shift. |
 |
Fig. 4 Normalized relaxation stress response: deformation independence. |
 |
Fig. 5 Shear storage modulus response vs. frequency at different predeformation levels. |
 |
Fig. 6 Loss factor vs. frequency at different predeformation levels. |
3 Finite strain viscoelastic models analysis
3.1 Models under consideration
The models under consideration are integral-based finite strain viscoelastic models, with the assumption of separability of time and strain effects [28,14]
-
Christensen model (1a) which consists on a viscoelastic generalisation of the kinetic theory of rubber elasticity with specific attention to stress-imposed problems;
-
Fosdick and Yu model (1b), based on the Quasi Linear Viscoelastic model, consists on a simple convolution between the Cauchy stress tensor
 and the relative Green-Saint-Venant deformation gradient E
t
(s);
and the relative Green-Saint-Venant deformation gradient E
t
(s); -
Simo model (1c), proposed in 1987, based on an uncouple volumetric and deviatoric response over any range of deformation, with decomposition of the stress tensor into initial and nonequilibrium parts. We denote that the Simo model is used in finite element software Abaqus [29].
For an homogeneous, isotropic and incompressible material, the originally proposed Christensen and Fosdick and Yu models were introduced with respect to a Neo-Hookean elastic potential. Considering this elastic potential, the hysteris stress part in the Simo model have been found to be strain-history independent. Herein, we make use of a generalisation of Christensen [30] and Fosdick and Yu [16] models.
For an homogeneous, isotropic and incompressible material, the constitutive relations for respectively Christensen, Fosdick & Yu and Simo models are: (1a)
(1a)
where  is the deformation gradient, while x is the position vector in the current configuration of a material particle which was located at position X in the reference configuration. The right and left Cauchy-Green strain tensor are consecutively C = F
T
F and B = FF
T
. The Green-Saint-Venant strain tensor is
is the deformation gradient, while x is the position vector in the current configuration of a material particle which was located at position X in the reference configuration. The right and left Cauchy-Green strain tensor are consecutively C = F
T
F and B = FF
T
. The Green-Saint-Venant strain tensor is  . The compressibility constraint,
. The compressibility constraint,  , is taken into account by adding a pressure field p
I depending on the intial and boundary conditions [4]. g1(t) is the dimensionless relaxation kernel defined as a Prony series and commonly taken as:
, is taken into account by adding a pressure field p
I depending on the intial and boundary conditions [4]. g1(t) is the dimensionless relaxation kernel defined as a Prony series and commonly taken as: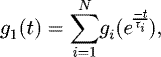 (2)
(2)
where G0 is the instantaneous shear modulus, and
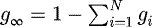 is the dimensionless long term shear modulus.
is the dimensionless long term shear modulus.
The convolution integral-based approach is based on the relative deformation gradient F t (s) = F(s)F −1(t) which is the deformation gradient at the current time s at the current configuration, as described in Figure 7.
For the Simo model, the “Dev” operator is defined as:
For the monotonic tests we have seen a material stiffness increasing for large deformations. Moreover, for the dynamic tests strain levels are of a low value, hence, we consider a Mooney-Rivlin elastic potential: (3)
(3)
where C1 and C2 are the Mooney-Rivlin material parameters.
The first Piola-Kirchoff stress Π, commonly known as nominal stress, will be used for experimental considerations, and is related to the Cauchy stress tensor as: (4)
(4)
 |
Fig. 7 Deformation gradient with respect to configurations. |
3.2 Uniaxial tension
We consider an uniaxial tension test. The transformation has the form: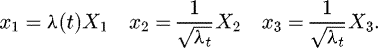 (5)
(5)
The deformation gradient and the right Cauchy-Green strain tensor have components:
For a Mooney-Rivlin elastic potential, the uniaxial tension equations are then: (7a)
(7a)
Since the available experimental data for uniaxial tension are only for monotonic testing, we consider the elongation function as: (8)
(8)
with 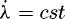 . The integration of those equations have been done using numerical approximation methods [31].
. The integration of those equations have been done using numerical approximation methods [31].
3.3 Simple shear motion
We consider a simple shear motion. The (non-symmetric) deformation gradient has components: (9)
(9)
The right Cauchy-Green strain tensor: (10)
(10)
The left Cauchy-Green strain tensor: (11)
(11)
Introducing equation (5) in equation (1a)–(1c), we obtain following relations: (12a)
(12a)
It is to denote that for the originally proposed Christensen and Fosdick & Yu models, and for a Mooney-Rivlin elastic potential: (13)
(13)
3.3.1 Monotonic shear test
For a monotonic shear relaxation test, we have: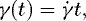 (14)
(14)
with  .
.
Substituting equation (14) in equation (12a)–(12c) we obtain the following governing Cauchy stress equations: (15a)
(15a)
3.3.2 Stress relaxation test
For a stress relaxation test: (16)
(16)
where H(t) is the Heaviside function. Hence, for a shear relaxation test the governing Cauchy stress equations are: (17a)
(17a)
For a very long relaxation time i.e t→ ∞, the equation (17a)–(17c) give the same expression for the shear relaxation: (18)
(18)
3.3.3 Determination of the complex shear modulus
The determination of the complex shear modulus was introduced by Christensen [32] and is a Fourrier transform of the governing equations. The frequency domain viscoelasticity is defined for a kinematically small perturbation about a predeformed state. The procedure consists on a linearised vibration solution associated with a long-term hyperelastic material behavior. This assumes that the linear expression for the shear stress still governs the system.
Therefore, we used the following state of loading: (19)
(19)
with
We assume that |γ
a
| << 1 and that the specimen has been oscillating for a very long time so that a steady-state solution is obtained and the dynamic stress has the form: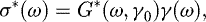 (20a)
(20a)
where G s = ℜ [G * (ω, γ0)] and G l = ℑ [G * (ω, γ0)] are respectively the shear storage and loss modulus expressed in term of the Fourrier transform of the time-dependent shear relaxation modulus.
Taking into account only first order terms of γ(ω), calculations leads to respectively Christensen (21a), Fosdick and Yu (21b) and Simo (21c):
 (21c)
(21c)
 is the dynamic stress component that should be additioned to the equilibrium static stress
is the dynamic stress component that should be additioned to the equilibrium static stress  component to obtain the total stress quantity.
component to obtain the total stress quantity.
The determinated complex shear modulus for the considered models is then: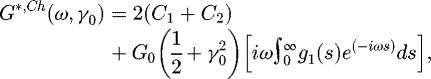 (22a)
(22a)
4 Results and discussion
The applied procedure to identify material’s parameters in an integral-based constitutive viscoelastic relationship relies on a stress decomoposition into a long-term response and an instantaneous part intended to deal with strain-rate dependence. In the present work, identification has been conducted with the “Evaluate” module of the finite element solver Abaqus 6.14 [29] and we wont report identification results. It is to underline that for the monotonic tests, at high strain values, a third order Ogden model [4] presents more accurate results for the pure hyperelastic response. To compare moderate strains, a simple Mooney-Rivlin leads to sufficient results (Tab. 1).
On the comparison results, we firstly present results for the monotonic tension response, as shows Figure 8. The three models presents the capability to take into account a strain rate effect, with higher stain rates leading to a higher stress at same deformation level. Nevertheless, for the considered strain rates, the Christensen model is not able to predict the experimental data for strains exceeding 50%. It is seen to excessively overestimate the stress. Fosdick and Yu model presents an instability at very low strains. This phenomena can be explained by the work of Kwon [15] on stability of seperable integral based viscoelastic models. The Simo model is also seen not able to fit experimental data for strains exceeding 50%. These observations are mainly related to the choice of the hyperelastic potential.
Secondly, we present results for the monotonic shear response, as shows Figure 9.
For both presented strain rates 5% min and 20% min, the experimental data are well approximated only for low strain levels, not to exceed 40% of deformation. The Christensen model quickly predict a material stiffening, which experimentally is not seen until 300% of deformation. Fosdick and Yu and Simo models slightly overestimates the experimental data till 40% of deformation. Over this limit, the error is seen to be of a large value.
Results for the shear relaxation test are graphically shown in Figure 10. Herein, it have been predicted that the stress response approximates asymptotically an equilibrium stress part, valued σ Equilibrium, at low deformation level while at higher level of 30%, this equilibrium stress is over estimated. The major difference of the three models is seen for the hysteritic part. Compared to the experimental data, Christensen model is seen to overestimate the stress for low times, and approximates the equilibrium stress for larger times. This observation is clearly revealed for the curve at 10% of deformation. Fosdick & Yu and Simo models are seen to slightly underestimate the experimental data, for low and high strains. At the beginning of relaxation, it is observed that the Simo model approximates better the experimental data (Tab. 2).
The comparison of the resulting complex shear modulus is evaluated in term of shear storage modulus and loss factor for all the models under consideration.
We firstly report on the results concerning the shear storage modulus, which are shown in Figures 11 and 12. Elastomers show a frequency dependent dynamic behavior. Increasing frequency leads to increasing the shear storage modulus in our frequency range. All investigated models exhibit this dependence. At 10% of predeformation, both Christensen and Fosdick and Yu models estimate the experimental data with good accuracy, while Simo model overestimates this modulus.
Considering the predeformation effect, experimental observations show that increasing static predeformation decreases the shear modulus, as shows Figure 5. Comparing the different models response, Christensen model shows an increase for the evaluated property with increased predeformation from 10 to 30% of deformations. Fosdick and Yu does not take into account this effect and exhibit the same response for both predeformed state while Simo model shows the most accurate shear dependency response with a considerable improvement for higher frequencies of 30 Hz.
Results concerning the loss factor are graphically shown in Figures 13 and 14. The frequency dependence of the three compared models is pronounced. Focusing on the predeformation effect, we can observe that Fosdick & Yu model still does not take this dependence into account. The estimated loss factor is of same value at 10 and 30% of static deformation. The Christensen and Simo models are seen to predict the loss factor with a good accuracy.
Monotonic tests relative errors.
 |
Fig. 8 Uniaxial tension monotonic response: comparison of the three models. |
 |
Fig. 9 Simple Shear monotonic response: comparison of the three models. |
 |
Fig. 10 Shear relaxation response, same response for infinite times. |
Relaxation test prediction relative errors.
 |
Fig. 11 Shear Storage Modulus response at 10% of predeformation: Experimental and models response. |
 |
Fig. 12 Shear Storage Modulus response at 30% of predeformation: Experimental and models response. |
 |
Fig. 13 Loss factor at 10% of predeformation: experimental and models response. |
 |
Fig. 14 Loss factor at 30% of predeformation: experimental and models response. |
5 Conclusion
In the present work, some experimental results on a filled rubber material have been presented. Three classical integral-based finite strain viscoelastic model, under the separability assumption, have been investigated, with more interest to a simple shear motion. The presented results allow us to draw the following conclusions concerning their prediction capabilities for the effective experimental observations:
-
•
the three models can predict the strain-rate dependence for the monotonic tests. Nevertheless, a good material's parameters identification is required to accurately reproduce the experimental data. The choice of the Hyperelastic potential and his stability limit is determinant on the predicted data;
-
•
for the shear relaxation process, we have observed a separability effect on experimental data. The predicted relaxation curves would reproduce the equilibrium stress with a good accuracy, although the hysteritic stress is not well approximated by the Christensen model. It have been found that the Simo model is the well adapted for this load path;
-
•
concerning the complex shear modulus;
-
–
All the models were able to predict that the material stifffens with increasing frequency. This observation is explicitly described by the strain-rate dependence in the time domain. The observed error of response level is mainly related to the predeformation effect;
-
–
The Christensen model has revealed to be unable to describe the softening due to the static predeformation. Such behavior is observed for some unfilled rubber materials. Thus, this model is better adapted for unfilled rubbers, none for filled ones;
-
–
Fosdick & Yu model, based on the QLV model introduced firstly to describe soft biological tissues, takes into account the frequency dependence and none the predeformation dependence of the material behavior;
-
–
Simo model shows a significant better estimate of the evaluated dynamic properties. It have shown the better predicting capability. This model offers too the facility to be implemented in finite element codes.
-
–
Finally, the considered models are based on the assumption of separability of strain and time effects, with a minimal set of identified material’s parameters. Although the Simo model considers uncoupled deviatoric and volumetric stress components, it shows good prediction capability for the dynamic properties of filled rubber materials.
Acknowledgment
This work contains partial results from the ENIT/ECL/Airbus Defence & Space Project that is financially supported by Airbus Defence and Space. We thank very sincerely all the partners associated for the realization of this work: Bernard Troclet and Stephane Muller.
References
- L.R.G. Treloar, The physics of rubber elasticity, Oxford University Press, 1975 [Google Scholar]
- W.N. Findley, F.A. Davis, Creep and relaxation of nonlinear viscoelastic materials, Courier Corporation, 2013 [Google Scholar]
- A.G. James, A. Green, G.M. Simpson, Strain energy functions of rubber. I. Characterization of gum vulcanizates, J. Appl. Polym. Sci. 19 (1975) 2033–2058 [Google Scholar]
- R.W. Ogden, Non-linear elastic deformations, Courier Corporation, 1997 [Google Scholar]
- F.J. Lockett, Creep and stress-relaxation experiments for non-linear materials, Int. J. Eng. Sci. 3 (1965) 59–75 [Google Scholar]
- R.A. Schapery, A theory of non-linear thermoviscoelasticity based on irreversible thermodynamics, in: 5th Nat. Cong. Appl. Mech., ASME, New York, 1966, pp. 511–530 [Google Scholar]
- K.C. Valanis, Unified theory of thermomechanical behavior of viscoelastic materials, in Procceding of Symposium Mechanical behavior of materials under dynamic loads, Springer, Texas, 1968, pp. 343–364 [CrossRef] [Google Scholar]
- R.M. Christensen, L. Freund, Theory of viscoelasticity, J. Appl. Mech. 38 (1971) 720 [Google Scholar]
- A. Amin, A. Lion, S. Sekita, Y. Okui, Nonlinear dependence of viscosity in modeling the rate-dependent response of natural and high damping rubbers in compression and shear: Experimental identification and numerical verification, Int. J. Plast. 22 (2006) 1610–1657 [CrossRef] [Google Scholar]
- B.D. Coleman, W. Noll, Foundations of linear viscoelasticity, Rev. Mod. Phys. 33 (1961) 239 [Google Scholar]
- M. Green, A. Tobolsky, A new approach to the theory of relaxing polymeric media, J. Chem. Phys. 14 (1946) 80–92 [Google Scholar]
- F. Sidoroff, Variables internes en viscoélasticité i. variables internes scalaires et tensorielles, J. Méc. 14 (1975) 545–566 [Google Scholar]
- F. Sidoroff, Variables internes en viscoélasticité, 2. milieux avec configuration intermédiaire, J. Méc. 14 (1975) 571–595 [Google Scholar]
- J. Sullivan, K. Mazich, Nonseparable behavior in rubber viscoelasticity, Rubber Chem. Technol. 62 (1989) 68– 81 [CrossRef] [Google Scholar]
- Y. Kwon, K.S. Cho, Time-strain nonseparability in viscoelastic constitutive equations, J. Rheol. (1978-present) 45 (2001) 1441–1452 [CrossRef] [Google Scholar]
- J. Ciambella, A. Paolone, S. Vidoli, A comparison of nonlinear integral-based viscoelastic models through compression tests on filled rubber, Mech. Mater. 42 (2010) 932–944 [Google Scholar]
- R.M. Christensen, A nonlinear theory of viscoelasticity for application to elastomers, J. Appl. Mech. 47 (1980) 762– 768 [Google Scholar]
- R. Fosdick, J.-H. Yu, Thermodynamics, stability and non-linear oscillations of viscoelastic solids II. History type solids, Int. J. Non-linear Mech. 33 (1998) 165–188 [CrossRef] [Google Scholar]
- J.C. Simo, On a fully three-dimensional finite-strain viscoelastic damage model: formulation and computational aspects, Comput. Methods Appl. Mech. Eng. 60 (1987) 153–173 [Google Scholar]
- H. Bechir, A. Kaci, Comparaison du module complexe d'Young résultant de deux différents modèles visco-hyper-élastiques, Rhéologie 6 (2004) 25–30 [Google Scholar]
- D.J. Charlton, J. Yang, K.K. Teh, A review of methods to characterize rubber elastic behavior for use in finite element analysis, Rubber Chem. Technol. 67 (1994) 481–503 [CrossRef] [Google Scholar]
- A. Lion, C. Kardelky, The Payne effect in finite viscoelasticity: constitutive modelling based on fractional derivatives and intrinsic time scales, Int. J. Plast. 20 (2004) pp. 1313–134. [CrossRef] [Google Scholar]
- D. Wollscheid, A. Lion, Predeformation-and frequency-dependent material behaviour of filler-reinforced rubber: Experiments, constitutive modelling and parameter identification, Int. J. Solids Struct. 50 (2013) 1217–1225 [Google Scholar]
- N.W. Tschoegl, The phenomenological theory of linear viscoelastic behavior: an introduction, Springer Science and Business Media, 2012 [Google Scholar]
- J.L. Sullivan, Viscoelastic properties of a gum vulcanizate at large static deformations, J. Appl. Polymer Sci. 28 (1983) 1993–2003 [CrossRef] [Google Scholar]
- A.R. Payne, R.E. Whittaker, Dynamic properties of materials, Rheologica Acta 9 (1970) 97–102 [Google Scholar]
- M. Rendek, A. Lion, Amplitude dependence of filler-reinforced rubber: Experiments, constitutive modelling and FEM Implementation, Int. J. Solids Struct. 47 (2010) 2918–2936 [Google Scholar]
- R. Bloch, W. Chang, N. Tschoegl, Strain independent nonlinearity in peroxide-cured styrene-butadiene rubber, J. Rheol. (1978-present) 22 (1978) 33–51 [CrossRef] [Google Scholar]
- Abaqus Theory Manual, version 6.14, section 4.8.2 [Google Scholar]
- E. Yang, Phenomenological Constitutive Models for Dielectric Elastomer Membranes for Artificial Muscle Applications, Thesis, 2006 [Google Scholar]
- J. C. Simo, T. J. Hughes, Computational inelasticity, Vol. 7. Springer Science and Business Media, 2006 [Google Scholar]
- R. Christensen, Theory of viscoelasticity: an introduction, Academic Press, NewYork, 1971 [Google Scholar]
Cite this article as: N. Jridi, M. Arfaoui, A. Hamdi, M. Salvia, O. Bareille, M. Ichchou, J. Ben Abdallaha, The capability of three seperable finite-strain viscoelastic models to predict response of a filled rubber material, Mechanics & Industry 19, 502 (2018)
All Tables
All Figures
 |
Fig. 1 Non-equilibrium stress response at different strain-rates. |
| In the text | |
 |
Fig. 2 Time independent equilibrium stress–strain curve. |
| In the text | |
 |
Fig. 3 Relaxation spectrum at different deformation levels: quasi-linear shift. |
| In the text | |
 |
Fig. 4 Normalized relaxation stress response: deformation independence. |
| In the text | |
 |
Fig. 5 Shear storage modulus response vs. frequency at different predeformation levels. |
| In the text | |
 |
Fig. 6 Loss factor vs. frequency at different predeformation levels. |
| In the text | |
 |
Fig. 7 Deformation gradient with respect to configurations. |
| In the text | |
 |
Fig. 8 Uniaxial tension monotonic response: comparison of the three models. |
| In the text | |
 |
Fig. 9 Simple Shear monotonic response: comparison of the three models. |
| In the text | |
 |
Fig. 10 Shear relaxation response, same response for infinite times. |
| In the text | |
 |
Fig. 11 Shear Storage Modulus response at 10% of predeformation: Experimental and models response. |
| In the text | |
 |
Fig. 12 Shear Storage Modulus response at 30% of predeformation: Experimental and models response. |
| In the text | |
 |
Fig. 13 Loss factor at 10% of predeformation: experimental and models response. |
| In the text | |
 |
Fig. 14 Loss factor at 30% of predeformation: experimental and models response. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.