| Issue |
Mechanics & Industry
Volume 21, Number 3, 2020
|
|
|---|---|---|
| Article Number | 306 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.1051/meca/2020014 | |
| Published online | 03 April 2020 | |
Regular Article
SOFC modelling considering radiation heat transfer
1
Laboratory of Thermal Processes, Research and Technology Center of Energy, Borj-Cedria, BP95 Hammam-Lif 2050, Tunisia
2
Physics Department, Faculty of Science, King Khalid University, PO Box 9004, Abha 61413, Saudi Arabia
* e-mail: alimi_wael@yahoo.com
Received:
29
October
2019
Accepted:
9
February
2020
In this study, the influence of radiation heat transfer within a planar SOFC is investigated. The numerical model is made by performing two-dimension mathematical model describing mass, momentum and heat transport phenomena coupled with electrochemical reactions. The finite volume method is used to solve the governing equations. Compared with literature results, the simulations show that radiation reduces temperature gradients and has a significant effect on enhancing heat transfer within the SOFC and counter balancing thermal dissipation induced by activation, concentration and ohmic polarisations. Thus, it must be included for an accurate model.
Key words: Planar SOFC / overpotential / radiation / finite volume method
© AFM, EDP Sciences 2020
1 Introduction
Nowadays Solid Oxide Fuel Cells (SOFC) are the subject of growing interest because of their higher actual and potential performances in terms of heat and electric power. In fact, the hot temperatures of rejected gas, about 800 °C allow an interesting valorization by adding a cogeneration combined cycle to the SOFC unit. The SOFC has an electric efficiency around 50% and when coupled to a gas turbine with an alternator, the efficiency can reach 70% with input pressurized gas. It is also possible to use the exhausted gas calories in order to cogenerate steam and electricity so the global efficiency in terms of heat and electricity can be superior to 80%. The high operating temperature range from 800 °C to approximately 1000 °C permitting an internal reforming of the fuel (for example methane) under the action of the water steam inside the SOFC. The efficiency of this operation is much higher than in case of external reforming for a Proton Exchange Membrane Fuel Cell (PEMFC). Actually, there are two main technologies for SOFC, tubular and planar geometries. The manufacturer Westinghouse develops the first one, which is in form of tubes pilled together. The ionic current (O2 –) passes from inside the tube where the air flows to outside where fuel, Hydrogen or methane is circulating. The planar technology, developed by manufacturer such as Siemens and Sulzer, is relatively recent. It is composed of sandwich of ceramic layers (anode, electrolyte and cathode) with interconnector separating fuel and oxidant and offers better performance compared to tubular technology. A Nickel/Zirconia (Ni-YSZ) anode, doped Lanthanum Strontium Ferrite (LSF) or doped Lanthanum Strontium Manganite (LSM) cathode, and Yttria Stabilized Zirconia (YSZ) electrolyte compose a typical planar SOFC. The performance of SOFC depends on heat, mass and charge transport occurring simultaneously inside it and on electrochemical and fluids processes, which affect strongly its efficiency and power. These phenomena need to be explored and clarified by means of experiments or physical and mathematical modelling. Heat transfer occurs in form of conduction in solid parts, convection in flow channels and porous electrodes and radiation in both solid and porous media. Since SOFC operates at high temperature, the radiation heat cannot be neglected and needs to be investigated when modelling thermal process. Many studies took in consideration radiation transfer in their models. They are varied from extremely simplified to comprehensive and complex numerical calculations solved often with commercial CFD and the results are sometimes confusing or conflicting, due to the lack in experimental data for radiative proprieties of electrodes and electrolyte. Hartvigsen et al. [1] are the first researcher who included radiation term to their model and conclude that it has a significant influence on the results. Murthy et al. [2] used Schuster–Schwarzschild method to model radiation transfer in electrolyte, considered as an optically thin body and they used Rosseland diffusion approximation for electrodes considered as an optically thick body to prove the importance of radiation heat transfer. The mathematical model of Damn et al. [3,4] showed that radiation can be excluded in the electrodes but not in electrolyte, and they found that its overall impact on temperature field in SOFC is relatively small. Daun et al. [5] compared results obtained by pure conduction model and combined conduction-radiation calculation and concluded that the difference between them is relatively small.
Several SOFC modelling studies appeared last years, trying to investigate radiation heat effect such as the works of Grzegorz Brus et al. [6], Kee et al. [7], Bao et al. [8], Imen Majeri et al. [9], García-Camprubí et al. [10] and Ferrero et al. [11]. However, all the existing models considered only ohmic heat by joule effect, neglecting radiation heat in the energy equation and didn't take into account other possible heat sources caused by concentration and activation overpotentials and chemical reaction such as the work of Ismet Tikiz et al. [12] and van Biert et al. [13]. However, this is not a reasonable simplification due to the complex properties of the SOFC materials.
The aim of the present study is to investigate the radiation heat influence in a typical planar SOFC by including all possible heat sources that occur inside it. This is done by developing a comprehensive numerical model in the different layers with various geometries in order to validate these assumptions often simplifying computational task.
2 Modeling approach
The studied physical model is shown in Figure 1, it is a planar SOC fed with Hydrogen as a fuel and Oxygen as oxidant. The electrochemical equations at the anode, cathode and the overall equation are respectively: (1)
(1)
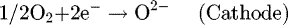 (2)
(2)
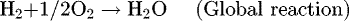 (3)
(3)
 |
Fig. 1 Schematic representation of the studied SOFC. |
2.1 Governing equations
Heat, mass and charge transfer as well as electrochemical reactions occur simultaneously within the SOFC and are strongly coupled. Thus, these phenomena affect the global performance of the cell and needed to be investigated. The next sections are dealing with their mathematical modeling.
2.1.1 Mass conservation
The species balance equation is: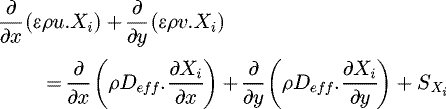 (4)
(4)
Xi
is the species mass fraction (i = O2, H2, H2O), ϵ is the porosity, D
eff is the effective diffusion coefficient in porous electrodes defined by 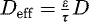 , ρ is the mass density and (u,v) are velocity components. The source term SXi
is related to the electrochemical reactions taking place in the electrolyte/electrode interface and it is written as follows:
, ρ is the mass density and (u,v) are velocity components. The source term SXi
is related to the electrochemical reactions taking place in the electrolyte/electrode interface and it is written as follows: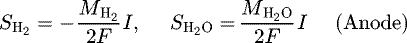 (5)
(5)
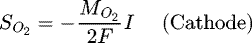 (6)with I is the current density.
(6)with I is the current density.
2.1.2 Momentum conservation
The gas flow throughout the porous electrodes is described by the Darcy's law: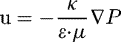 (7)
(7)
P is the pressure, κ is the permeability and μ is the viscosity. This equation is coupled with the continuity equation: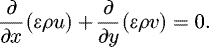 (8)
(8)
2.1.3 Energy conservation
The energy balance law can be written as follows: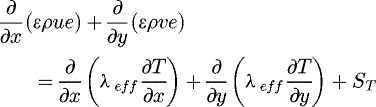 (9)
e is the gas internal energy, λeff
is the effective conductivity determined by: λ
eff
= ϵλ
g
+ (1 − ϵ)λ
s
, T is the temperature and ST
is the heat source. ST
is the sum of all generated/dissipated heat:
(9)
e is the gas internal energy, λeff
is the effective conductivity determined by: λ
eff
= ϵλ
g
+ (1 − ϵ)λ
s
, T is the temperature and ST
is the heat source. ST
is the sum of all generated/dissipated heat: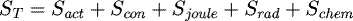 (10)
(10)
−S
joule
is the Joule effect heat due to electronic resistance in the electrodes and ionic resistance in the solid electrolyte and it is calculated as follows: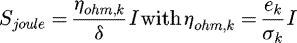 (11)
(11)
ηohm
presents the Ohmic polarisation or overpotential, ek
is the thickness and σk
is the electrical conductivity given by Yixiang et al [14]: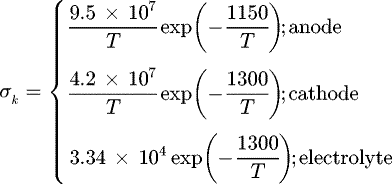 (12)
δ presents the thickness of the region where heat is dissipated.
(12)
δ presents the thickness of the region where heat is dissipated.
– S
act
is the heat due to activation overpotential in the electrodes calculated by: (13)
ηact,k
is the activation overpotential and i0,k
is the exchange current density defined by:
(13)
ηact,k
is the activation overpotential and i0,k
is the exchange current density defined by: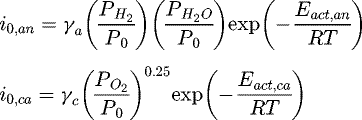 (14)
γk
is a factor depending on the reaction, Eact
is the activation energy, F stands for the Faraday number, P
0 is the gas pressure at the electrode/electrolyte interface and R is the perfect gas constant.
(14)
γk
is a factor depending on the reaction, Eact
is the activation energy, F stands for the Faraday number, P
0 is the gas pressure at the electrode/electrolyte interface and R is the perfect gas constant.
– Scon is the heat due to the concentration overpotentials in the electrodes expressed by: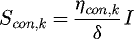 (15)with [16]:
(15)with [16]: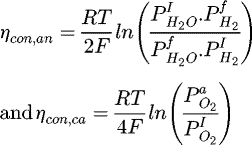 (16)presenting the concentration overpotentials in the cathode or anode assuming that the electrochemical reactions occur only at the electrode/electrolyte interface. PI
is the gas partial pressure at the electrode/electrolyte interface, calculated for each species as follows:
(16)presenting the concentration overpotentials in the cathode or anode assuming that the electrochemical reactions occur only at the electrode/electrolyte interface. PI
is the gas partial pressure at the electrode/electrolyte interface, calculated for each species as follows: (17)– S
chem
is the heat generated by the chemical reaction at the interface of anode/electrolyte; and can be expressed in term of enthalpy [17]:
(17)– S
chem
is the heat generated by the chemical reaction at the interface of anode/electrolyte; and can be expressed in term of enthalpy [17]: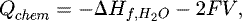 (18)
(18)
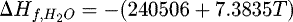 (19)is the enthalpy formation of water and:
(19)is the enthalpy formation of water and: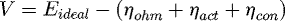 (20)being the cell tension. Eideal
is the ideal potential calculated by:
(20)being the cell tension. Eideal
is the ideal potential calculated by: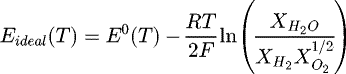 (21)and
(21)and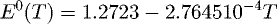 (22)
(22)
Therefore the expression of the chemical heat source is: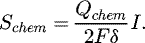 (23)
(23)
The electrodes are supposed as an optically Thick body (τ
L=βL
>>1. The radiative heat flux is estimated through Rosseland approximation: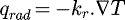 (24)where kr
is the radiative conductivity defined as [3–5]:
(24)where kr
is the radiative conductivity defined as [3–5]: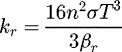 (25)
βr
refers to the Rosseland-mean extinction coefficient, σ is the Stefan-Boltzmann constant, and n is the refractive index. The electrolyte is supposed gray non-scattering medium and optically thin (τ
L=βL
≪ 1). Thus we can use the two–flux model proposed by Schuster–Schwarzschild to evaluate the radiative heat as [3–5]:
(25)
βr
refers to the Rosseland-mean extinction coefficient, σ is the Stefan-Boltzmann constant, and n is the refractive index. The electrolyte is supposed gray non-scattering medium and optically thin (τ
L=βL
≪ 1). Thus we can use the two–flux model proposed by Schuster–Schwarzschild to evaluate the radiative heat as [3–5]: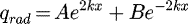 (26)
A, B are given by:
(26)
A, B are given by: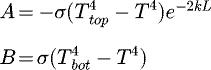 (27)
Ttop
and Tbot
are the two temperatures of the two isothermal sides of the medium separated by a distance L. The radiative source is obtained from the radiative heat flux by:
(27)
Ttop
and Tbot
are the two temperatures of the two isothermal sides of the medium separated by a distance L. The radiative source is obtained from the radiative heat flux by: (28)
(28)
2.2 Model implementation
The considered governing equations are solved numerically by using the finite volume method, which consists of dividing the computational domain as shown in Figure 2, into a number of control volumes, each one surrounding a grid point and then integrating the differential equations over each control volume in order to obtain the discretised equations. The numerical code is written in a self-programming FORTRAN language. The numerical resolution is carried out with a SOFC properties and operating conditions summarized in Table 1.
The numerical simulations are validated with experimental results of Zhao et al. [18] and the current–voltage curve was generated by the model for different values of operating temperatures (temperatures at channels flow entries) as shown in Figure 3. The simulated results have similar shape compared to the experimental data and become mush closer at higher temperatures. At higher currents, the concentration overpotentials become important and produce a voltage drop in the cell which results to the tailing effect observed in the curve at temperature 1073 K.
 |
Fig. 2 Computation domain and boundaries conditions. |
 |
Fig. 3 Comparison between simulated and experimental cell voltages. |
3 Results and discussion
3.1 SOFC performances
The cell voltage and power density versus current density simulated by the model for the input parameters are presented in Figure 4. The curves are plotted for various operating temperatures (at flow channels entries): 1000 K, 1100 K, 1200 K, and 1300 K and for three types of geometry of a planar SOFC namely: anode supported, electrolyte supported and cathode supported cell. The corresponding dimensions are set in Table 2.
At temperature 1000 K, the electrolyte supported SOFC shows the worst performance in terms of cell voltage and power density because of the high ohmic polarisation. However as the temperature increases, the power density in the cathode supported SOFC decreases until becoming small in comparison to the power density in the electrolyte supported geometry at temperature 1200 K (0.45 W/cm2 to 0.49 W/cm2). This is can be explained by the fact of growth of its cathodic concentration polarisation precisely which depends essentially on the oxygen diffusion process that becomes slower, due firstly to the used thick cathode and secondly to the poor effective oxygen gas diffusion coefficient which diminishes with increasing current density.
It should be noted that the cell voltage in case of cathode supported drop to zero when the current density reach approximately 0.5 A/cm2 for all the range of temperatures. At this point, the cell attain its limits, but the values of cell voltage remain higher than in case of electrolyte supported, 0.95V for first case to 0.9 V for last one at 1300°K. The anode supported SOFC shows the best performance among the two other geometries. Its maximum power density increases from 0.32 W/cm2 at 1000 K to 1.22 W/cm2 at 1300 K with a current density equal to 0.7 A/cm2 and 1.5 A/cm2 respectively. The cell voltage exhibits a tail effect as the temperature increases due to the important concentration polarization which plays a crucial role at higher current densities.
According to Figure 5 (case of anode supported SOFC) for a temperature of 1000 K, the cell voltage decreases from its Nernst Potential value to 0.035 V which corresponds to a current density equal to 1.3 A/cm2. The power density increases to reach a pick value equal to 0.324 W/cm2 when the current density is equal to 0.65 A/cm2 and the cell voltage is equal to 0.5V. In this condition, the major tension loss is due to both ohmic and activation polarisations, after that the former overpotential became the main loss and the power density decreases to 0.05W/cm2 corresponding to 1.3A/cm2 as current density and 0.1V as cell voltage. The concentration polarization remains small and then plays a minor role.
 |
Fig. 4 Comparison of performance among anode, electrolyte and cathode supported SOFC. (a) T = 1000 K, (b) 1100 K, (c) 1200 K and (d) 1300 K. |
Dimension of the planar cell.
 |
Fig. 5 Cell voltage, polarisation and power density versus current density at 1000 K for anode supported SOFC. |
3.2 Radiation effect on SOFC
In this section, the numerical results of two geometric configurations, anode supported (AS) and electrolyte supported (ES) are presented since they are the most developed and used in the industry because of their better electric performances. First, the operating temperature influence is examined for two cases: heat source with and without radiation and then the current density influence is also investigated in order to have a better idea on the effect of radiation heat.
3.2.1 Operating temperature influence on SOFC
3.2.1.1 SOFC-AS
The temperature field through the SOFC is shown in Figure 6 for various operating temperatures ranging from 1000 K to 1300 K with and without radiation heat. The shape of temperature distribution is the same for all cases. In fact, there is an increase of temperature in the entire cell and hot temperatures are located in the electrolyte and near the interconnectors, due to the important heat dissipation by joule effect in the electrolyte and chemical reaction heat at the interface anode/electrolyte and especially the high heat resistance of the interconnector which constitutes a barrier to heat transfer and resulting in the accumulation of heat in these regions. As the operating temperature is increased, the difference between maximum and minimum temperature ΔT decreases from 8.307 at 1000 K to 2.396 at 1300 K without radiation, and from 8.077 at 1000 K to 2.260 at 1300 K with radiation term, as illustrated in Table 3. This is because at higher temperatures the heat transfer by conduction becomes important and tends to make temperature field homogeneous in the entire SOFC. In addition, the radiation decreases the rise of temperature in the SOFC by enhancing heat transfer within it especially at intermediate temperatures and ceases to have an effect at higher temperatures as traduced by the difference ΔTmax = ΔTwithout radiation − ΔTwith radiation.
 |
Fig. 6 SOFC-AS temperature field. |
Temperature effect.
3.2.1.2 SOFC-ES
In case of supported electrolyte, the same observations seen in the previous case remained valid as shown in Figure 7. Except that the difference in temperature between maximum and minimum ΔT are much greater than in case of anode supported SOFC due to the higher ohmic overpotential in the thick electrolyte, from 10.920 at 1100 K to 3.677 at 1300 K, without radiation and from 10.523 at 1100 K to 3.468 at 1300 K with radiation.
High temperatures are located near the interconnectors and the maximum is in the electrolyte zone. As the temperature increases, the electrical conductivity is improved resulting in weak ohmic overpotential and then the heat is mainly transported by conduction. The radiation also enhances the heat diffusion, decreases temperature in the cell, and becomes negligible while temperature increases as illustrated by ΔT max in Table 3.
 |
Fig. 7 SOFC-ES temperature field. |
3.2.2 Current density influence on SOFC
3.2.2.1 SOFC-AS
With increasing current densities, the temperature inside the cell increased since the different overpotentials and its relative heats depends on current density as shown in Figure. 8. For temperature equal to 1000 K, the difference ΔT without radiation rises from 2.539 at I = 0.4 A/cm2 to 16.831 at I = 1.2 A/cm2 and by varying the operating temperature to 1200 K and 1300 K, it decreases each time by half as the electrical conductivity increases (Tab. 4).
When adding the radiation, the same thing is observed. By varying the current density, ΔT with radiation increases from 2.470 at I = 0.4 A/cm2 to 16.354 at I = 1.2 A/cm2 at temperature 1000 K. For relatively high temperature equal to 1300 K the rise of temperature is decreased as the radiation improves the heat diffusion and then its effect is minimized. In Table 4, ΔT max traduces the difference between the two cases, with and without radiation.
 |
Fig. 8 Temperature field for anode supported SOFC under current density effect. |
Current effect on anode supported SOFC.
3.2.2.2 SOFC-ES
In the case of electrolyte supported, the temperature fields at I = 0.4 A/cm2 and I = 1.2 A/cm2 at 1300 K are illustrated in Figure 9, and the same phenomenon are observed. However, the temperature rise within the SOFC is much greater than in case of anode supported geometry due to the joule heat losses in the thick electrolyte. Also the radiation affect globally the temperature distribution by decreasing the maximum temperature when current density is increased and become relatively negligible when operating at higher temperatures, as indicated by the differences ΔT without radiation, ΔT with radiation and ΔT max in Table 5.
 |
Fig. 9 Temperature field for electrolyte supported SOFC under current density effect. |
Current effect on electrolyte supported SOFC.
4 Species distributions in the SOFC
Figure 10 shows the different species mass distribution in the fuel cell, Hydrogen, water steam and Oxygen for anode-supported configuration. The results are carried out at operating temperature value of 1300 K and current density I equal to 1.5 A/cm2. For the reactive H2 and O2, their mass fraction decrease in the direction of interface with the electrolyte where the reactions take place and maximal fractions are located near the channel flow interface. However, for water produced in gaseous phase in the interface anode/electrolyte, important fractions reach the interface and accumulated at the interconnectors where high values are reached.
 |
Fig. 10 Species mass fraction distribution; for an average current density I = 1.5A/cm2 and operating temperature T=1300 K. |
5 Conclusion
The results obtained by the present numerical modelling lead to interesting conclusions. First, anode and electrolyte supported SOFCs show the best electric performances in terms of current and power densities especially at higher operating temperatures. Activation and ohmic polarisation are the main dominant voltage losses in the cell when the current increases and therefore it is reflected in power density and corresponding heat sources. Radiation plays a significant role on SOFC temperature distribution especially in electrolyte semi-transparent media which allows heat transfer by radiation within it. In the contrary, electrodes supposed as an optically thick media have a minor effect. In fact, radiation improves the thermal diffusion inside the cell and counterbalance heat dissipation by ohmic and activation polarisations as well as reaction heat and the result is a decrease in temperatures especially in electrolyte. As the operating temperature increases, the effect of radiation becomes weak is and tend to homogenise the temperatures field. At higher current densities, the radiation influence becomes more significant within the cell, which allows concluding that when modelling thermal transport and heat management of SOFC, the radiation contribution should be taken into account especially when the cell operates at high current and intermediate temperature.
Nomenclature
Cp : Specific heat at constant pressure [J kg−1 K−1]
Di : Molecular diffusivity [m2 s−1]
Deff : Average effective diffusivity [m2 s−1]
E0 : Open-circuit voltage at standard pressure [V]
ek : Thickness of each layer [μm]
F : Faradays constant [96,485 A s mol−1]
k : Absorption coefficient [m−1]
ΔH : Enthalpy change of reaction, [J mol−1]
i0 : Exchange current density [A m−2]
n : Refractive index of the medium
qrad : Radiative heat flux [W m−2]
R : Gas constant [8.3145 J mol−1 K−1]
Greek symbols
βr : Extinction coefficient [m−1]
δ : Layer thickness, where heat is produced [μm]
λ : Thermal conductivity [W m−1K−1]
γ: Pre exponential factor of the exchange current density, [A m−2]
σ : Ion/electron conductivity [Ω−1 m−1]
τL : Total optical length of a medium
Abbreviations, subscripts and superscripts
act : Activation (polarization)
con : Concentration (polarization)
I : Interface electrode/electrolyte
k : Anode cathode or electrolyte
References
- J. Hartvigsen, S. Elangovan, A. Khandkar, Modeling, design, and performance of solid oxide fuel cells, Proc. Sci. Technol. Zirconia 682–693 (1993) [Google Scholar]
- S. Murthy, A.G. Fedorov, Radiation Heat Transfer Analysis of the Monolith-Type Solid Oxide Fuel Cell, J. Power Sources 124, 453–458 (2003) [Google Scholar]
- D.L. Damm, A.G. Fedorov, Spectral radiative heat transfer analysis of the planar SOFC, J. Fuel Cell Sci. Technol, 2, 258–262 (2005) [Google Scholar]
- D.L. Damm, A.G. Fedorov, Radiation heat transfer in SOFC materials and components, J. Power Sources 143, 158–165 (2005) [Google Scholar]
- K.J. Daun, S.B. Beale, F. Liu, Radiation heat transfer in planar SOFC electrolytes, J. Power Sources 157, 302–310 (2006) [Google Scholar]
- B. Grzegorz, J.S. Szmyd. Numerical modelling of radiative heat transfer in an internal indirect reforming-type SOFC, J. Power Sources 181, 8–16 (2008) [Google Scholar]
- R.J. Kee, B.L. Kee, J.L. Martin, Radiative and convective heat transport within tubular solid-oxide fuel-cell stacks, J. Power Sources 195, 6688–6698 (2010) [Google Scholar]
- C. Bao, N. Cai, E. Croiset, An analytical model of view factors for radiation heat transfer in planar and tubular solid oxide fuel cells, J. Power Sources 196, 3223–3232 (2011) [Google Scholar]
- I. Mejri, A. Mahmoudi, M.A. Abbassi, A. Omri, Radiation Heat Transfer Effect in Solid Oxide Fuel Cell: Application of the Lattice Boltzmann Method, International Journal of Mathematical, Computational, Physical, Electrical Comp. Eng. 8 (2014) [Google Scholar]
- M. Garcia-Camprubi, H. Jasak, N. Fueyo, “CFD analysis of cooling effects in H2-fed solid oxide fuel cells” J. Power Sources 196, 7290–7301 (2011) [Google Scholar]
- D. Ferrero, A. Lanzini, M. Santarelli, Solid Oxide Fuel Cells Modeling, Advances in medium and high temperature solid oxid fuel cell technology, CISM Int. Centre Mech. Sci. 574, 291–342 (2017) [CrossRef] [Google Scholar]
- I. Tikiz, Huseyin Pehlivan, CFD modelling and experimental validation of cell performance in a 3-D planar SOFC, Int. J. Hydrogen 44, 15441–15455 (2019) [CrossRef] [Google Scholar]
- L. van Biert, M. Godjevaca, K. Visser, P.V. Aravind, Dynamic modelling of a direct internal reforming solid oxide fuel cell stackbased on single cell experiments, Appl. Energy 250, 976–990 (2019) [Google Scholar]
- S. Yixiang, C. Ningsheng, L. Chen, Numerical modelling of an anode-supported SOFC button cell considering anodic surface diffusion, J Power Sources 164, 639–48 (2007) [Google Scholar]
- M. Ni, M.K.H. Leung, D.Y.C. Leung, Parametric study of solid oxide fuel cell performance, Energy Convers. Manag. 48, 1525–1535 (2007) [Google Scholar]
- P. Aguiara, C.S. Adjiman, N.P. Brandon, Anode-supported intermediate temperature direct internal reforming solid oxide fuel cell. I: model-based steady-state performance, J. Power Sources 138, 120–136 (2004) [Google Scholar]
- M. Chnani, Modelisation Macroscopique de piles PEFC et SOFC pour l'étude de leur couplage, Thèse de doctorat. Institut FEMTO-ST- Département ENISYS UMR CNRS 6174–UFC – ENSMM – UTBM. (2008) [Google Scholar]
- F. Zhao, A.V. Virkar, Dependence of polarization in anode-supported solid oxide fuel cells on various cell parameters, J. Power Sources 141, 79–95 (2005) [Google Scholar]
- CFD Fluent 6.2.16 [Google Scholar]
Cite this article as: W. Alimi, R. Chouikh, A.A. Guizani, SOFC modelling considering radiation heat transfer, Mechanics & Industry 21, 306 (2020)
All Tables
All Figures
 |
Fig. 1 Schematic representation of the studied SOFC. |
| In the text | |
 |
Fig. 2 Computation domain and boundaries conditions. |
| In the text | |
 |
Fig. 3 Comparison between simulated and experimental cell voltages. |
| In the text | |
 |
Fig. 4 Comparison of performance among anode, electrolyte and cathode supported SOFC. (a) T = 1000 K, (b) 1100 K, (c) 1200 K and (d) 1300 K. |
| In the text | |
 |
Fig. 5 Cell voltage, polarisation and power density versus current density at 1000 K for anode supported SOFC. |
| In the text | |
 |
Fig. 6 SOFC-AS temperature field. |
| In the text | |
 |
Fig. 7 SOFC-ES temperature field. |
| In the text | |
 |
Fig. 8 Temperature field for anode supported SOFC under current density effect. |
| In the text | |
 |
Fig. 9 Temperature field for electrolyte supported SOFC under current density effect. |
| In the text | |
 |
Fig. 10 Species mass fraction distribution; for an average current density I = 1.5A/cm2 and operating temperature T=1300 K. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


