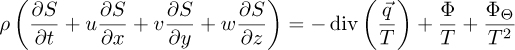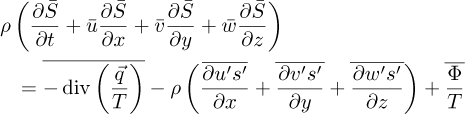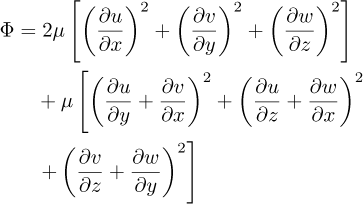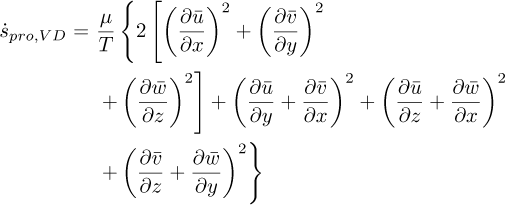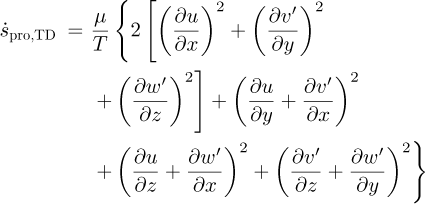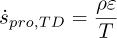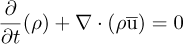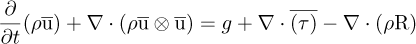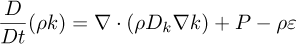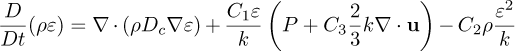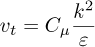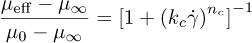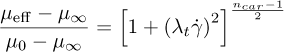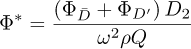| Issue |
Mechanics & Industry
Volume 25, 2024
High fidelity models for control and optimization
|
|
|---|---|---|
| Article Number | 13 | |
| Number of page(s) | 15 | |
| DOI | https://doi.org/10.1051/meca/2024009 | |
| Published online | 18 April 2024 | |
Regular Article
Energy loss analysis of volute centrifugal pump handling non-Newtonian emulsions through entropy production theory
1
LIFSE, Arts et Métiers Institute of Technology, CNAM, HESAM University,
F-75013
Paris,
France
2
LEMI, FT, University of M’hamed Bougara,
Avenue de L’indépendance,
Boumerdes
35000,
Algeria
3
Department of Energy and Automation, Universidad Metropolitana, UNIMET,
Venezuela
* e-mail: lila.achour@ensam.eu
Received:
3
February
2023
Accepted:
4
April
2024
Flow losses in centrifugal pumps handling non-Newtonian fluids are of great importance for design optimization, performance prediction, and energy savings. Traditional methods are very limited in determining energy losses due to the complex rheological behavior of such fluids. This study aims to investigate the hydraulic losses and performance degradation mechanism of centrifugal volute pumps handling non-Newtonian emulsions using the entropy production method, focusing on the influence of emulsion type on the loss mechanism. The influence of pump size on fluid’s non-Newtonian behavior and energy loss in a centrifugal pump is also investigated by comparing the entropy distribution in two geometrically similar pumps operating with different emulsions exhibiting shear-thinning behavior. The flow field and entropy production are predicted by computational fluid dynamics (CFD) based on the Reynolds-averaged Navier-Stokes (RANS) equations coupled with the k-epsilon turbulence model. The latter is used to acquire the dissipative entropic components of the flow. The results showed that for a non-Newtonian fluid, energy loss occurs primarily in the impeller, regardless of pump size and flow rate. In addition, the shear-thinning behavior of concentrated emulsions significantly affects hydraulic losses, especially in small-size pumps. Most importantly, small-size pumps generate relatively the highest entropy loss over the entire flow range and the entropy loss increases with the lower limit of the non-Newtonian plateau. This approach showed that the predominance of losses in centrifugal volute pumps operating with non-Newtonian fluids depends on the pump size. Thus, indicating that the hydrodynamic characteristics of two geometrically similar pumps do not scale when the liquid has non-Newtonian rheology.
Key words: Entropy production / emulsions / non-Newtonian / CFD / hydraulic losses / pump size
© L. Achour et al., Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
The two-phase liquid-liquid flows are present in almost all engineering and industrial processes. An instance of this type of flow is the liquid-liquid mixture of water and viscous oil commonly experienced in the petroleum industry. An important characteristic of these mixtures is their non-Newtonian rheology, particularly a shear-thinning behavior [1,2] an apparent viscosity that is typically above the viscosity of the separated liquids [3–5]. Therefore, their presence may be detrimental to some industrial equipment. The last case involves centrifugal pumps, a type of fluid-handling machinery that is extensively utilized in industry and is specifically designed to pump water or low-viscosity fluids. The rheological behavior of these mixtures causes complications in the operation of the centrifugal pumps. Thus, their behavior is affected by the rheological properties of the mixture, which has proven to be a decisive factor in their performance [6–8]. Given the enormous influence of non-Newtonian rheology on pump performance, the research of centrifugal pumps handling non-Newtonian oil-water dispersions has gained importance in recent years. For instance, numerous studies have shown that the head and flow rate of centrifugal pumps are reduced when handling an oil-in-water emulsion [6], and this reduction depends on the rheology of the mixture, which varies with the microstructure of the emulsion [4,9,10], chemistry of the coexisting phases and its stability [11–13]. Besides, the forces acting on the liquid-liquid dispersions define the rheological behavior of these mixtures. A quantitative relationship between shear stress and effective viscosity is frequently observed in centrifugal pumps owing to the fluid's non-Newtonian behavior [14]. In Valdes’ experiment with an electrical submersible pump (ESP) handling oil-in-water mixtures [15] with various concentrations, the authors observed non-Newtonian properties with a narrower effective viscosity range for the water-in-oil (W/O) emulsion and a pronounced shear thinning behavior for the oil-in-water (O/W) emulsion. Accordingly, a non-Newtonian behavior is commonly observed in the flow of emulsions, wherein the most cases, a high shear rate resulting from the pump impeller rotation lowers the fluid viscosity. The investigations on internal flow analysis of centrifugal pumps and their performances in the presence of non-Newtonian fluids have shown that non-Newtonian fluids with high apparent viscosity cause significant performance degradation, especially at high flow rates. In contrast, fluids with low apparent viscosity behave like water [16]. In addition, non-Newtonian rheological behavior can be beneficial for centrifugal pump operation under certain operating conditions [17]. As noticed in [18], the non-Newtonian behavior, particularly the shear thinning characteristic increases the pump's head while decreasing the braking power required and allows for a wider operating range without affecting pump efficiency at higher flow rates.
When selecting centrifugal pumps for use with non-conventional fluids, the estimation of the characteristic curve is essential for pump selection since the characteristic curve of these pumps under non-Newtonian fluid flow is unknown. Thorough investigations have been conducted on the influence of viscosity on pump performance by developing several theoretical and semi-empirical correlations [19–24]. These studies provide models that depend on pump geometry and fluid viscosity to calculate the associated theoretical head degradation, but these correlations find their limits when the fluid is non-Newtonian. Nevertheless, few cases have attempted to propose correlations for estimating the non-Newtonian rheology of liquid-liquid mixtures in centrifugal pumps based on experimental data. These correlations were then coupled with a one-dimensional model to predict the performance of the ESP [25], or a mechanistic model based on the different losses, namely frictional, impact, and recircula-tion losses for the prediction of pump performance [26,27]. However, the empirical aspect of the rheological model raises questions regarding the universal validity of such a combination for inferring the pump performance when handling emulsions. Moreover, the manufacturing history of pumps handling non-Newtonian fluids can also be difficult because the characteristics of the fluid can change abruptly in a short time [24] and these different physical processes can become limiting at different pump scales. For centrifugal pumps carrying non-Newtonian fluids, the influence of pump size on the complex rheological behavior of the pumped fluid is not mentioned, nor is the underlying cause and hydraulic loss mechanism caused by non-Newtonian rheology clearly illustrated. Thus, the lack of knowledge about the effect of pump size on non-Newtonian fluid behavior makes scaling up a centrifugal pump directly from the laboratory to the industrial scale an open issue. This hinders the selection of centrifugal pumps for application to non-Newtonian fluids. Therefore, research is needed to investigate the energy loss induced by the flow of non-Newtonian fluids in a centrifugal pump. The energy performance of hydraulic machines can be quickly evaluated using the energy loss by entrop generation approach. Recently, this method is increasingly adopted in the evaluation of energy losses in turboma-chinery, especially due to advances in theoretical and computer developments and the evolution of technology [28].
Many researchers have used the entropy production theory to investigate the effects of some parameters like impeller tip clearance [29–31], clocking position [32,33], impeller trimming [34], and blade thickness [35,36] on the internal flow field and the hydraulic losses of pumps. Also, for identifying the process mechanism of hydraulic losses and the fluid flow state in the different components of specific types of hydraulic machinery, including centrifugal pumps [37–40], mixed and axial flow pumps [29], and hydro-turbine [41–45]. Most of these studies were collected in the review article [28], where the authors emphasized the importance of entropy production theory in the study of the internal flow mechanism of turboma-chinery, the evaluation of their hydraulic performance and the optimization of pump design.
The main contribution of this study is to establish a relationship between the non-Newtonian rheological behavior of emulsions and the energy loss in a volute centrifugal pump using the entropy production method. Furthermore, to study the influence of pump size on the non-Newtonian behavior and entropy production by comparing the energy performance of two geometrically similar pumps handling non-Newtonian emulsions. The emulsions were modeled in this study as a single-phase fluid exhibiting shear thinning behavior. This assumption implies that the fluids are homogeneous and that the specific interactions related to the two-phase nature are neglected. The CFD models were validated against experimental data for water, considering steady and unsteady approaches. The results obtained in this work showed that the non-Newtonian behavior of the fluid, specifically its pseudo-plasticity, has a significant impact on the entropy generation in a volute centrifugal pump. Besides, the entropy generated for both pumps over the entire flow range is much higher relatively to the pump volume in the small-size pump and depends on the lower bound of the non-Newtonian viscosity.
2 Entropy production theory
Entropy production refers to thermodynamic irreversibil-ity and energy loss in a system. In centrifugal pumps, the impeller's kinetic energy is transformed into pressure energy, resulting in an irreversible energy loss and an increase in entropy due to the viscosity of the working fluid, the turbulent flow regime and the high Reynolds stress. According to the second law of thermodynamics, flow losses are energy losses that can be identified by determining the entropy production which is a relevant variable to measure these hydraulic losses. Especially since the working fluid has a complex rheological behavior and other methods (analytical methods) of quantifying losses have proven to be limited [14,26,27]. This method is therefore used to explain the mechanism of the different energy losses in two similar pumps handling non-Newtonian fluids. The specific entropy S, a state variable, for an incompressible single-phase flow is given by equation (1) [28].
The negative term 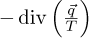 is the reversible heat transfer.
is the reversible heat transfer. 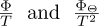 represent the entropy production caused by dissipation and heat transfer respectively.
represent the entropy production caused by dissipation and heat transfer respectively.
According to the time-averaged Reynolds process, the specific entropy in turbulent flow is separated into the time-averaged component S and the fluctuating parts’. The entropy transport equation wihin the pump is then provided by equation (2) since the flow is assumed to be isothermal without heat transfer.
The viscous dissipation function for the incompressible flow is defined in equation (3) [46].
From the time-averaged Reynolds process, the specific entropy production for the main flow (Eq. (4)) is divided into time-averaged part ṡpro,VD, which is caused by viscous dissipation, and fluctuating terms ṡpro,TD which are caused by turbulence. The entropy production rate by viscous dissipation given by equation (5) is directly calculated from CFD. While the entropy production caused by turbulence given by equation (6) cannot be determined directly from the CFD since the RANS model does not calculate fluctuating velocities. This quantity is however directly related to the chosen turbulence model and is determined using equation (7) [47], where ε stands for the turbulent dissipation rate.
In addition to the previously mentioned entropy generation, there is also entropy generation at the walls. This is because rotating fluid machines’ blade surfaces have high velocity and pressure gradients, which cause a strong wall effect in the flow field and nontrivial irreversible flow losses [28]. The following expression is used to compute the entropy produced at the walls of the grid's initial layer.
where v is the fluid velocity at the first grid close to the wall and τ represents the wall’s shear stress. In the end, the total entropy production (TEP) is the product of the surface integral of the entropy production at the walls (Eq. (9)) and the volume integral of the local entropy production rate due to viscous and turbulent dissipation.
3 Numerical modelling
The numerical simulations are carried out on two geometrically similar centrifugal pumps handling non-Newtonian emulsions. A similarity ratio of 1/5 is chosen to reach a laboratory scale dimension while maintaining the same flow regime (similar Reynolds range and close specific speeds). Both pumps operated with highly turbulent flows as shown by the Reynolds number computed for water in Table 1. These pumps consist of a semi-open impeller with five backward curved blades and a volute. The main geometric and operating characteristics of these pumps are summarized in Table 1. Three-dimensional turbulent flow modeling using a RANS approach is performed on the impeller-volute assembly as well as the suction and discharge pipes. The emulsions were assumed to be single-phase with non-Newtonian behavior and the flow is incompressible, turbulent, and viscous. The fluid equations were discretized using the finite volume method (FVM) in CFD simulations using the open-source package OpenFOAM v1906. The following sections provide a summary of the numerical methods.
Pump specifications and Reynolds number ranges: large-scale pump (pump A) and scaled-down model (pump B)
3.1 Pumps geometry and grid
The flow domain of the two scale pumps was modeled in four parts. Taking the example of the large-scale pump (pump A), as shown in Figure 1a, it is mainly divided into impeller, volute, suction, and discharge pipes. The inlet and outlet parts have been extended to avoid any back-flow phenomenon at the inlet and outlet of the pump. The three-dimensional volumetric fluid is meshed with a polyhedral grid in the impeller and volute due to the complex geometry of these parts. A hexahedral structured grid is adopted for the inlet and outlet pipes. The impeller wall is given a boundary layer mesh, which results in an average y+ < 5 and a direct resolution of the inner region’s viscous sublayer. To guarantee the grid independence of the findings, a mesh sensitivity analysis was carried out. Readers are invited to refer to [48] for more details.
 |
Fig. 1 Calculation domains and grid. |
3.2 Governing equation and turbulence model
The mass and momentum equations, expressed by equations (10) and (11), are solved simultaneously with the SIMPLE algorithm since the pumped fluid is incompressible and the flow is in a steady state.
where  is the averaged stress tensor and R is the Reynolds stress tensor. This simulation is modeled through the multi-reference frame (MRF) technique which allows to drastically reduce computational time. The MRF approach is used for modeling relative motion between the pump stationary part (volute, inlet pipe, and outlet pipe) and the rotating impeller. This approach considers the rotation of the impeller without moving the mesh. It divides the computational domain into a part simulated in a rotating reference frame, for which the equations are solved with the Coriolis term added to the momentum equation while the other part is simulated in a fixed reference frame. To solve the Reynolds averaged governing equations, the k – epsilon model was chosen. The simulation was conducted using both k – epsilon and k – ω models, and no differences were observed in the results. However, the k – epsilon model exhibited better stability and convergence, leading to its selection. This model is composed of the dissipation rate equation ε and the turbulent kinetic energy k given by the following equations:
is the averaged stress tensor and R is the Reynolds stress tensor. This simulation is modeled through the multi-reference frame (MRF) technique which allows to drastically reduce computational time. The MRF approach is used for modeling relative motion between the pump stationary part (volute, inlet pipe, and outlet pipe) and the rotating impeller. This approach considers the rotation of the impeller without moving the mesh. It divides the computational domain into a part simulated in a rotating reference frame, for which the equations are solved with the Coriolis term added to the momentum equation while the other part is simulated in a fixed reference frame. To solve the Reynolds averaged governing equations, the k – epsilon model was chosen. The simulation was conducted using both k – epsilon and k – ω models, and no differences were observed in the results. However, the k – epsilon model exhibited better stability and convergence, leading to its selection. This model is composed of the dissipation rate equation ε and the turbulent kinetic energy k given by the following equations:
where Dk, P, Dε, Cµ, νt, and C1, C2 are the effective diffusivity for k, turbulent kinetic energy production rate, effective diffusivity for ε, the model coefficient for the turbulent viscosity, turbulent viscosity and model coefficient, respectively.
At the intake of the upstream pipe, a velocity inlet following the volumetric flow rate in use and a turbulence intensity of 5% was imposed. Static pressure was considered at the outlet of the downstream pipe. The pump’s whole interior was configured with no-slip velocity conditions. By contrasting the simulation results with the water experiment data, the numerical model was proven to be accurate. For complete details on numerical model validation and grid sensitivity, the reader is referred to our previous paper [48].
3.3 Emulsions rheology modeling
The experimental findings of Valdes et al. [15] on two-phase mixtures of sunflower oil and water served as the foundation for the emulsions examined in the current numerical investigation. Their investigation covers a wide range of oil concentrations, from 90%–10% O/W to 10%–90% O/W with 10% increments. Following the analysis of the oil-water mixtures, three-phase morphologies were identified: a pseudo-stable water-oil emulsion (WC < 20%), a pseudo-stable concentrated water-oil emulsion (20% < WC < 40%), and a multi-regime emulsion (WC > 40%). The mixtures properties were investigated at shear rates ranging from 1 s−1 to 3000 s−1 and were then fitted to the traditional effective viscosity models of Cross and Carreau, given by equations (15) and (16), respectively.
λt and ncar are the relaxation time and the power index, respectively. While kc and nc are the Cross time and Cross rate constant. µ0 and µ∞ correspond to the viscosity for zero and very high shear rate. Three emulsions were considered in the present study, having the following oil concentrations: 40%, 70% and 80% by volume, each corresponding to a different morphology as shown in Table 2. Given the relatively small difference between emulsion densities, we assume that it has a negligible impact on the entropy produced in the pump.
4 Results and discussion
In this section, the CFD results of the two pumps handling different types of emulsion under different flow conditions are presented and compared. First, the effect of the non-Newtonian behavior on the overall performance of the pumps is analyzed. Then, a comparative analysis of entropy generation in the centrifugal pump when handling shear-thinning non-Newtonian fluids is reported, focusing on the effect of pump size.
4.1 Hydrodynamic characterization
The performance curves of the two pumps when operating with non-Newtonian emulsions are shown in Figure 2. The head, expressed as a non-dimensional coefficient 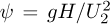 , and efficiency of each pump were calculated under different operating conditions, ranging from 0.2 Qbep to 1.4 Qbep and water values are included for comparison.
, and efficiency of each pump were calculated under different operating conditions, ranging from 0.2 Qbep to 1.4 Qbep and water values are included for comparison.
The analysis can be divided into two parts, the first part concerns the effect of non-Newtonian behavior on the pump performance. The second part concerns the effect of pump size on the hydrodynamic behavior when the fluid is non-Newtonian. As the flow rate increases from 0.2 Qbep to 1.4 Qbep, the head, and efficiency of both pumps decrease with increasing oil volume fraction. This can be attributed to the increase in hydraulic losses, which are driven by the increase in fluid viscosity and flow rate, as reported in previous studies [21,49]. This is expected since the viscosity of the emulsion increases with the oil concentration, leading to an increase in friction losses, which are governed by the fluid's viscosity. On the other hand, all the studied emulsions show a non-Newtonian behavior delimited by the upper and lower Newtonian plateaus, and the 70%O-30%W emulsion which is a concentrated pseudo-stable W/O emulsion corresponds to the phase inversion where the viscosity reaches the maximum [15]. However, it was noticed that the pump head obtained when handling the 70%O–30%W emulsion was higher than those observed for the 80%O–20%W emulsion under all operating conditions. This trend is observed in both pumps and is due to the strong shear thinning character of this mixture, where this feature improves pump performance compared to the performance developed for the 80%O– 20%W emulsion. As a function of the applied shear rate, the viscosity of these emulsions decreases according to the shear thinning behavior to approach the infinite viscosity delimiting the rheological model. The same remarks were noted in the experimental study of Valdes and all [15] with an ESP when handling these emulsions, where they highlighted that the non-Newtonian character can be beneficial for the performance of a multistage pump. The results presented above highlight the effect of non-Newtonian rheology on the performance characteristics of centrifugal pumps.
Regarding the influence of pump size on hydrodynamic behavior, it is clear that the hydrodynamic characteristics do not scale when the fluid is non-Newtonian between the two pumps even if the similarity condition is respected. The performance degradation of the smaller pump is slightly higher than that of the larger pump, especially under overload conditions. The effect of pump size on the head and efficiency curves depends on the shear thinning behavior of emulsions and mainly on the lower Newtonian plateau delimiting its viscosity. As this limit increases, the degradation of the small-size pump becomes more significant. On average, the most oil-concentrated emulsion 80%O–20%W) which is the most viscous obtained a 22% head degradation in the large-size pump versus 32% in the small-size one at overload conditions (1.2 Qbep). On the other hand, the 40%O–80%W that has the lowest viscosity range obtained a 7% head degradation in the large pump versus 13% in the scaled-down model. This can be attributed to the different energy losses occurring inside the pump, depending on the fluid's rheological behavior and the pump size. These results will be quantified in the next section by analyzing the entropy generated in both pumps operating with the different non-Newtonian mixtures, and giving a qualitative analysis of the flow fields inside the two pumps.
Comparing the performance obtained for water and emulsions from Figure 3, it is evident that the torque required for water is greater than that needed for emulsions. The torque is represented by the non-dimensional torque coefficient CT = (T/ρN2 D5) where T is the torque in (N m).
In terms of energy consumption, the shear-thinning behavior of emulsions favors their operation, resulting in viscosity drops near the shaft. Despite emulsions having higher viscosity compared to water, their shear-thinning behavior allows for easy guidance inside the impeller and the pump. This leads to lower torque and, consequently, lower energy consumption. These results emphasize that shear-thinning rheology of the fluid results in a decrease in outlet tangential velocity, which increases with increasing emulsion viscosity. This difference in tangential velocity can be attributed to minimal flow slip at the impeller outlet, indicating that shear-thinning rheology effectively minimizes slip in centrifugal pumps. Notably, the impact of fluid rheology and flow rate is more pronounced in small pumps, since the decrease in torque required to pump emulsions versus water is more pronounced for the small-size pump (Fig. 3, right).
 |
Fig. 2 CFD head of the large-size pump (a) and scaled-down pump (b), efficiency of the large-size pump (c) and scaled-down pump (d). |
 |
Fig. 3 Pump torque calculated from CFD for the large-size pump (left) and scaled-down model (right) handling different emulsions versus flow rate. |
4.2 Energy loss analysis by local entropy production
Figure 4 compares the TEP per volume of the two centrifugal pumps handling different non-Newtonian emulsions versus flow rate.
It can be observed that the TEP per volume in both pumps increases with the volume fraction of the oil phase, which is consistent with the increase in fluid viscosity.
It can be observed that the TEP per volume in both pumps increases with the volume fraction of the oil phase, which is consistent with the increase in fluid viscosity. When operating with water, the trend of the entropy production versus flow rate is the same in both pumps regardless of their size, but the amplitude is almost three times higher in the small-size pump. As expected, the TEP of the centrifugal pumps increases as the flow rate deviates from the design point. It increases slightly under overload conditions and increases more importantly as the flow rate decreases. This indicates that the hydraulic losses caused by the secondary vortex structure and recirculation zones increase, as shown in Section 4.4. Similar observations were reported in previous studies [46].
However, for non-Newtonian mixtures, the influence of the pump size on the energy loss is more prominent. With the emulsion's concentration changing, the entropy production in the large-size pump when operating with non-Newtonian fluid varies in a similar trend to that of water, except for the 80%O–20%W emulsion for witch the TEP decreases at overload conditions. This can be explained by the viscous forces that overcome the convec-tive forces due to the higher viscosity of this emulsion, so the flow becomes less turbulent in all parts of the pump. The entropy caused by turbulence, which is predominant here decreases significantly, resulting in a decrease in total entropy. However, for the small size pump, the evolution of hydraulic losses for different emulsions seems to show an opposite trend. Namely, the increase in the oil concentration i.e., the increase in fluid's viscosity, results in a slight increase in entropy generation at partial operating conditions and a significant increase as the flow rate increases. This implies firstly that the hydraulic losses caused by turbulence and vortex structure when operating with non-Newtonian fluid are more significant in the large-size pump under partial operating conditions, relatively to the total losses. Secondly, in the small-size pump, as the flow rate increases, the hydraulic losses become more significant as the viscosity of the emulsions increases, and can probably be attributed to incidence and shock losses. These types of losses are indeed the most dominant at high flow rates. Moreover, the difference between the entropy generated for water and the different emulsions is larger in the reduced model. This explains the more pronounced performance degradation in the small-size pump observed previously when the fluid is non-Newtonian. Hereof, it can be concluded that the losses will be different in two geometrically similar pumps depending on the non-Newtonian behavior of the mixture. To further investigate this point, a detailed analysis of the different losses in the two pumps is given in the next section.
 |
Fig. 4 Total entropy production of the large size pump (left) and scaled-down model (right) handling different emulsions versus flow rate. |
4.3 Effect of pump size and non-Newtonian rheology on entropy distribution
To clarify the mechanism of energy loss in two geometrically similar pumps handling non-Newtonian fluids, the TEP distribution in both domains, including impeller and volute as a function flow rate is presented in Figure 5 for each fluid.
The predominance of losses within parts of a centrifugal volute pump depends on the fluid viscosity and pump size as observed in the figure. Before the design flow rate, the TEP in the impeller is higher than the one in the volute for both pumps when handling water, but it becomes larger in the volute at overload conditions. As for emulsions, it is more dominant in the impeller than in the volute over the whole flow range and for both pumps. This difference in entropy generation in different parts of the pumps can be explained by the high rotational speed of the impeller, which generates more kinetic energy. As expected, the energy loss occurs mainly in the rotor region of centrifugal pumps. Both parts of the large-size pump (PA) are weekly affected by the variation of the non-Newtonian rhe-ology, where a similar level of entropy production in the impeller as well as in the volute is observed for all emulsions. On the other hand, the influence of emulsion type on entropy production is well observed in the different parts of the small-size pump. The TEP in the impeller shows a sharp increase with the flow rate as the oil volume fraction increases in the emulsion. At the same time, the increasing rate of TEP in the volute exhibit a lower slope as the flow rate increases, in comparison to the impeller. As shown above, pump size significantly affects the non-Newtonian behavior of emulsions and the associated losses.
Figures 6 and 7 show the fraction of each type of entropy produced in the pump domains relative to the total entropy at different operating condition i.e. 0.5 Qbep and Qbep. Water and concentrated emulsion 80%O–20%W have been chosen as reference fluids for the presentation of these results.
Using the same method for loss estimation, the study of Lai et al [50] on a volute centrifugal pump with a specific speed of 1579, a TEP in the main flow of 75W is obtained at 0.5 Qbep, which gradually decreases with increasing flow rate to reach its minimum value of 50W at the design point. The TEP then gradually increases with the increase in flow rate to 60W. Comparing these results with the small-size pump considered in this study that has approximately the same specific speed (1605), a TEP of 115W is obtained at 0.5 Qbep, which decreases to 80W at the design point, and increases slightly at higher flow rates.
At partial operating conditions, the rate of energy loss caused by turbulence decreases in the impeller as the oil volume fraction increases in the emulsion. On the other hand, in the volute, the rate of energy loss caused by turbulence increases as the oil volume fraction in the emulsion increases.
In addition, this type of entropy production is relatively more important in the impeller of the small-size pump than in the large-size pump when operating when water, and is smaller when operating with emulsions. This can be explained by the vortex zones that can be very large in the impeller of centrifugal pumps under partial operating conditions, generating a higher energy loss than in the volute. Moreover, the size of the vortex area depends on the pump size and is inversely proportional to the viscosity of the emulsions as mentioned in the previous study. Where the study showed larger recirculation zones in the inter-blade space of the small-size pump when handling water at low flow rates, compared to the large pump. On the other hand, when handling emulsions, smaller recircu-lation zones appear in the inter-blade space compared to the large-size pump. In both pumps, the percentage rate of energy loss caused by turbulence increases in the volute and decreases in the impeller as the flow rate increases for all fluids.
At the best efficiency point, the distribution of the different losses in the volute and the impeller is almost similar in both pumps when the fluid is non-Newtonian. However, when the fluid is water, the energy loss in the large-size pump occurs mainly in the volute, while in the small-size pump, the energy loss occurs mainly in the impeller. The entropy generation becomes increasingly important in the volute as the flow rate increases regardless of pump size but has a high fraction in the large-size pump as illustrated in Figure 8, which shows the fraction of each entropy production in the two domains of the two pumps when operating with water under three different operating conditions.
The results show that the amount of entropy created by direct dissipation is significantly less than that produced by turbulent dissipation in both pumps, especially when water is the working fluid. This result is consistent with earlier research [28,51] in which the authors concluded that the majority of the total entropy produced by the pump is due to turbulent dissipation entropy. For emulsions, the rate of energy loss by direct dissipation increased in the impeller and volute of both pumps with increasing oil concentration in the emulsion for all operating points. This is because when oil content rises, the emulsions' viscosity increases, promoting a rise in fric-tional losses while lowering secondary and recirculation losses. It should be noted that the method of calculating entropy production based on the CFD results depends on the turbulence model and the mesh resolution. A turbulence model is used to drive the numerical simulation to assess the impact of turbulence fluctuation on the mean fluid flow. A finer mesh would increase the entropy production by viscous dissipation, which is directly computed, and correspondingly decrease the entropy production by turbulence, which is modeled.
 |
Fig. 5 Influence of the emulsion type on the entropy production in the different parts of the large-size pump (PA) and the scaled model (PB). |
 |
Fig. 6 Fraction of each entropy production in the two domains of the two pumps versus the handled fluid in partial operation condition 0.5 Qbep. |
 |
Fig. 7 Fraction of each entropy production in the two domains of the two pumps versus the handled fluid at design condition Qbep . |
 |
Fig. 8 Fraction of each entropy production in the two domains of the two pumps when operating with water under three different operating conditions. |
4.4 Analysis of local entropy loss distribution
To comprehensively understand the effect of non-Newtonian behavior on the energy loss mechanism in two similar pumps, the distribution of normalized entropy production coefficient (EPC) calculated using equation (17) [32] is used to compare the locations of high dissipation values within the two pumps. Figures 9, 11 and 12 show the entropy distribution for all studied fluids under 0.5 Qbep, Qbep, and 1.2 Qbep operating points at the midspan plane.
As analyzed previously, the hydraulic losses in centrifugal pumps operating with non-Newtonian fluids depend on the pump size. In average, the small-size pump generates higher entropy loss compared to the large-size one, relatively to the pump volume.
Figure 9 shows the entropy distribution for all studied fluids under partial conditions at the midspan plane. The losses are concentrated at the impeller inlet, spiral volute part particularly in contact with impeller outlet, impeller inter-blade passage, and volute nozzle regions of both pumps at underload conditions.
Contrary to the impeller passage, the losses in the volute increased with increasing emulsion viscosity. In both pumps, the energy loss occurring at the impeller inlet increases with the concentration of oil in the emulsion. In addition, this energy loss is higher in the small-size pump, mainly when operating with high viscous emulsions. This entropy production at the impeller inlet probably results from the difference between the fluid inlet angle and the blade inlet angle, generating impact losses. Thus, shock losses increase as the viscosity of the fluid increases and the pump size is reduced. The losses occurring at the inter-blade space of the impeller decrease with oil concentration, and this decrease is more pronounced in the small-size pump. These areas of high entropy losses correspond to recirculation losses observed in the velocity field and streamlines within impeller inter-blade space, as shown in Figure 10.
The figure shows the velocity field and streamlines for two handled fluids at underload conditions, where a vortex area near the pressure side of the impeller blades is in contact with the volute tongue in both pumps. This vortex decreases as the volume fraction of the oil phase of the emulsions increases. In addition, this vortex is larger in the small-size pump than in the large-size one when handling water and is smaller when handling emulsions. These areas of recirculation and change of fluid direction cause the fluid to lose kinetic energy, which is the source of hydraulic losses, leading to an increased entropy generation. Regarding the losses at the spiral volute part, this last one is more significant in the reduced model and increases with increasing emulsions viscosity. These flow losses correspond to the flow entering the volute with a velocity angle that can deviate from that of the volute on which is superimposed a tangential velocity vortex opposite to the movement of the impeller [52]. This change in flow direction inevitably involves hydraulic losses. This suggests that the energy loss generated by recirculation zones will be smaller in a small-size pump than in a large-size pump when handling non-Newtonian fluid, and inversely for the volute diffusion losses. This results highlight that the volute diffusion losses are the predominant losses in both pumps.
At the design point, the entropy produced decreases as expected in the whole pump, and high-loss regions are mainly located in the impeller inlet, in the wake of the trailing edges, the volute's tongue, and the divergent as shown in Figure 11. Compared to underload conditions, the entropy generated at the impeller inlet decreases in the large-size pump for all fluids, however, in the small-size pump, this entropy decreases for water and less viscous emulsion. Moreover, the energy dissipation of the emulsion is more pronounced in the small pump as shown in the figure. After the nominal flow rate, the entropy generated in the inter-blade space decreases, and the entropy generated in the wake of the trailing edges are constantly high, especially for the small-size pump. Moreover, Figure 12 shows significant entropy generation regions at the tip and divergent of the volute.
By analyzing the flow field and velocity streamlines within these regions (Fig. 13b), we recognize a vortex zone near the volute tongue of the large-size pump that develops and moves toward the volute divergent as the fluid viscosity increases. For the scaled-down model, a small vortex zone appears in the volute divergent for 70%O-30%W emulsion. At overload conditions, a large recirculation zone appears in the divergent part of the volute and decreases as the oil volume fraction increases. This undesirable flow pattern produces the relatively high entropy loss observed previously. Regarding the entropy produced at the impeller inlet, we observe that it increased at overload conditions and with emulsion concentration. These results are consistent with the impact loss model, where previous studies [27,49] have shown that the impact loss decreases with increasing flow rates to reach its minimum at nominal flow rates, and increases as the flow rate increases above this point.
As shear-thinning emulsions pass through the impeller and pump components, their viscosity decreases in regions of high shear stress. This shear-thinning behavior, consistently observed in all the emulsions studied, is explained in Figure 14, which shows the distribution of the effective viscosity of a typical emulsion with an oil volume fraction of 80% versus flow rate. The figure illustrates a reduction in effective viscosity with increasing operating flow rates, consistent with the expected shear-thinning behavior of emulsions. In particular, the regions of high energy dissipation previously identified (impeller inlet and outlet, volute neck, blade surfaces and impeller-volute contact interface) correspond to the region of low viscosity in Figure 14.
The viscosity of the emulsion reaches its minimum at the pump walls (decreasing from 7.59 10−5 m2/s to 2.4 10−5 m2/s), which is caused by the high shear stress and generating friction losses. In addition, fluid viscosity decreases at the impeller inlet, probably due to the disparity between the fluid inlet angle and the blade inlet angle, which induces impact losses. Finally, we observe variations in emulsion viscosity at the inlet of the volute, which are more pronounced in the small-size pump, correspond to the fact that the flow enters the volute at a velocity angle that can deviate from that of the volute, with a superimposed tangential velocity vortex opposing the impeller motion. This change in flow direction generates a region of high shear stress, resulting in hydraulic losses. On the other hand, the smaller pump induces higher shear rates than the larger pump, resulting in lower viscosities for the emulsions in the reduced model, consistent with their shear-thinning behavior. This observation is illustrated in Figure 14, where the distribution of effective emulsion viscosity is significantly lower in the smaller pump. The results consistently show lower viscosities for all the emulsions studied in the reduced model due to the increased shear rate generated by the pump.
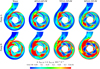 |
Fig. 9 Entropy production distribution at underflow condition 0.5 Qbep. |
 |
Fig. 10 Velocity distribution and streamlines on the impeller at 0.5 Qbep. |
 |
Fig. 11 Entropy production distribution at design condition Qbep. |
 |
Fig. 12 Entropy production distribution at overload condition1.2 Qbep. |
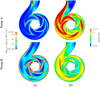 |
Fig. 13 Entropy production distribution (a) and the velocity streamlines (b) at overload condition 1.2 Qbep. |
 |
Fig. 14 Effective viscosity profiles for 80%O–20%W emulsion versus flow rate. |
5 Conclusion
Based on the entropy generation method, the influence of non-Newtonian fluid rheology on the internal flow fields of a volute centrifugal pump is numerically investigated. A dependency between the non-Newtonian rheological behavior and the energy loss mechanism in a volute centrifugal pump has been highlighted. Furthermore, the influence of the pump size on the non-Newtonian behavior and entropy production is investigated by comparing the energy performance of two geometrically similar pumps handling non-Newtonian fluids. The analysis is performed both quantitatively and qualitatively, and supported by general integrated quantities and observation of local flow features. Based on the analysis of the results, the following findings and conclusions are drawn:
The internal flow field of the centrifugal volute pump is affected by non-Newtonian rheology, which also contributes significantly to hydraulic losses and entropy generation in pumps. The entropy generation increases significantly as the lower limit of non-Newtonian viscosity increases and energy loss occurs primarily in the impeller, regardless of pump size and flow rate.
The pump size influences the non-Newtonian behavior of the fluid, and thus the flow structure and magnitude of losses. The smaller the pump size, the greater the entropy generation relative to the volume.
The predominance of losses in centrifugal volute pumps operating with non-Newtonian fluids depends on the size of the pump. More entropy production is generated at the leading and trailing edges of the smaller pump's impeller than the larger pump. Concluding that shock and change of direction losses will be more significant in a small-size pump, and the recirculation losses less prominent compared to a large-size pump when the fluid is non-Newtonian.
The energy loss increases with the concentration of oil in the emulsion and is predominantly experienced at the impeller input of the small-size pump as the flow rate rises. In contrast, in the large pump, the energy loss at the impeller inlet is generally small compared to that of the small pump, especially when comparing emulsions with high concentrations, but the difference remains insignificant for water and emulsions with low oil concentrations. In conclusion, pump size affects shock losses for highly viscous emulsions, but insignificantly for water and low viscosity emulsions.
Funding
The Article Processing Charges for this article are taken in charge by the French Association of Mechanics (AFM).
Conflicts of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Data availability statement
Data available in a publicly accessible repository that does not issue DOIs. This data can be found here: [https://www.dropbox.com/sh/ mdk6zn2ly77v0jt/AAB3NyGtoCBbE08v19aZP0jTa?dl=0]
Author contribution statement
All authors were involved in the design of the model and discussion of the results. Conceptualization L.A., M.S. and A.M.; writing original draft preparation L.A.; validation, review M.S., A.M, B.I and S.K.; supervision S.K. and I.B. All authors have read and agreed to the published version of the manuscript.
References
- H.P. Rønningsen, Rheology of petroleum fluids, Annual transactions of the Nordic rheology society 20, 11–18 (2012) [Google Scholar]
- J.P. Valdes, M. Asuaje, N. Ratkovich, Study of an ESP’s performance handling liquid—liquid flow and unstable O—W emulsions. Part II. Coupled CFD-PBM modelling, J. Petrol. Sci. Eng. 198, 108227 (2021) [CrossRef] [Google Scholar]
- S. Guet, O.M.H. Rodriguez, R.V.A. Oliemans, N. Brauner, An inverse dispersed multiphase flow model for liquid production rate determination. Int. J. Multiphase Flow 32, 553–567 (2006) [CrossRef] [Google Scholar]
- J. Plasencia, B. Pettersen and O. Jørgen, Pipe flow of water-in-crude oil emulsions: effective viscosity, inversion point and droplet size distribution, J. Petrol. Sci. Eng. 101, 35–43 (2013) [CrossRef] [Google Scholar]
- R.M. Perissinotto, W. Monte Verde, C.E. Perles, J.L. Biazussi, M.S. de Castro, A.C. Bannwart, Experimental analysis on the behavior of water drops dispersed in oil within a centrifugal pump impeller, Exp. Thermal Fluid Sci. 112, 109969 (2020) [CrossRef] [Google Scholar]
- M.F. Khalil, S.Z. Kassab, A.S. Ismail, I.S. Elazab, Centrifugal pump performance under stable and unstable oil-water emulsions flow, Twelfth International Water Technology Conference, January 2008, pp. 687–702 [Google Scholar]
- D. Croce, E. Pereyra, Study of oil/water flow and emulsion formation in electrical submersible pumps, SPE Prod. Oper. 35 (2019) 26–36 [Google Scholar]
- H. Banjar, H.Q. Zhang, Experiments and emulsion rheology modeling in an electric submersible pump, International Petroleum Technology Conference 2019 (IPTC 2019), 2019 [Google Scholar]
- N.A.V. Bulgarelli, J.L. Biazussi, W. Monte Verde, C.E. Perles, M.S. de Castro, A.C. Bannwart, A novel criterion based on slip ratio to assess the flow behavior of W/O emulsions within centrifugal pumps, Chem. Eng. Sci. 247, 117050 (2022) [CrossRef] [Google Scholar]
- J.C. Vielma, Rheological behavior of oil-water dispersion flow in horizontal pipes, PhD thesis, Citeseer, 2006 [Google Scholar]
- M.F. Ali, M.H. Alqam, Role of asphaltenes, resins and other solids in the stabilization of water in oil emulsions and its effects on oil production in Saudi oil fields, Fuel 79, 1309–1316 (2000) [CrossRef] [Google Scholar]
- S. Kokal, Crude-oil emulsions: a state-of-the-art review, SPE Prod. Facil. 20, 5–13, (2005) [CrossRef] [Google Scholar]
- N. Aske, H. Kallevik, J. Sjöblom, Water-in-crude oil emulsion stability studied by critical electric field measurements. Correlation to physico-chemical parameters and near-infrared spectroscopy, J. Petrol. Sci. Eng. 36, 1–17 (2002) [CrossRef] [Google Scholar]
- N.A.V. Bulgarelli, J.L. Biazussi, W. Monte Verde, C.E. Perles, M.S. de Castro, A.C. Bannwart, Experimental investigation on the performance of Electrical Submersible Pump (ESP) operating with unstable water/oil emulsions, J. Petrol. Sci. Eng. 197, 107900 (2021) [CrossRef] [Google Scholar]
- J.P. Valdes, M. Asuaje, N. Ratkovich, Study of an ESP's performance handling liquid-liquid flow and unstable O–W emulsions. Part I. Experimental, Chem. Eng. Sci. 223 (2020) [Google Scholar]
- N. Aldi, C. Buratto, M. Pinelli, P.R. Spina, A. Suman, N. Casari, CFD analysis of a non-Newtonian fluids processing pump, Energy Procedia 101, 742–749 (2016). [CrossRef] [Google Scholar]
- M. Donmez, O. Yemenici, A numerical study on centrifugal pump performance with the influence of non-Newtonian fluids, Int. J. Sci. 8, 39–45 (2019) [Google Scholar]
- J.P. Valdes, D. Becerra, D. Rozo, A. Cediel, F. Torres, M. Asuaje, N. Ratkovich, Comparative analysis of an electrical submersible pump's performance handling viscous Newtonian and non-Newtonian fluids through experimental and CFD approaches, J. Petrol. Sci. Eng. 187 (2020) [Google Scholar]
- A.T. Ippen, The influence of viscosity on centrifugal performance, Trans ASME 68, 1–18 (1946). [Google Scholar]
- J.F. Guölich, Pumping highly viscous fluids with centrifugal pumps – Part 1, World Pumps 1999, 30–34 (1999). [CrossRef] [Google Scholar]
- W.G. Li, Effects of viscosity of fluids on centrifugal pump performance and flow pattern in the impeller, Int. J. Heat Fluid Flow 21 , 207–212 (2000) [CrossRef] [MathSciNet] [Google Scholar]
- Hydraulic Institute, Effects of Liquid Viscosity on Rotodynamic (Centrifugal and Vertical) Pump Performance, 2004. [Google Scholar]
- W.G. Li, A method for analyzing the performance of centrifugal oil pumps, J. Fluids Eng. Trans. ASME 126, 482–485 (2004) [CrossRef] [MathSciNet] [Google Scholar]
- G. Amaral, V. Estevam, F.A. Franca, On the influence of viscosity on ESP performance, SPE Prod. Oper. 24, 303–310 (2009). [Google Scholar]
- N.A.V. Bulgarelli, J.L. Biazussi, W. Monte Verde, C.E. Perles, M.S. de Castro, A.C. Bannwart, Relative viscosity model for oil/water stable emulsion flow within electrical submersible pumps, Chem. Eng. Sci. 245, 116827 (2021) [CrossRef] [Google Scholar]
- J. Zhu, H. Zhu, G. Cao, H. Banjar, J. Peng, Q. Zhao, H.Q. Zhang, A new mechanistic model for oil-water emulsion rheology and boosting pressure prediction in electrical submersible pumps ESP, Proceedings – SPE Annual Technical Conference and Exhibition, January 2019, 2019 [Google Scholar]
- J. Zhu, H. Zhu, G. Cao, J. Zhang, J. Peng, H. Banjar, H.Q. Zhang, A new mechanistic model to predict boosting pressure of electrical submersible pumps under high-viscosity fluid flow with validations by experimental data, SPE J. 25, 744–758 (2020) [CrossRef] [Google Scholar]
- L. Zhou, J. Hang, L. Bai, Z. Krzemianowski, M.A. El-emam, E. Yasser, R. Agarwal, Application of entropy production theory for energy losses and other investigation in pumps and turbines: a review APEN-D-21-11938, Appl. Energy 318, 119211 (2022) [CrossRef] [Google Scholar]
- L. Ji, W. Li, W. Shi, H. Chang, Z. Yang, Energy characteristics of mixed-flow pump under different tip clearances based on entropy production analysis, Energy 199, 117447 (2020) [CrossRef] [Google Scholar]
- J. Cao, J. Pei, Y. Gu, W. Wang, S. Yuan, Flow losses analysis in a mixed flow pump with annular volute by entropy production evaluation, IOP Conf. Ser.: Earth Environ. Sci. 240 (2019) [Google Scholar]
- S. Shen, Z. Qian, B. Ji, Numerical analysis of mechanical energy dissipation for an axial-flow pump based on entropy generation theory, Energies 12 (2019) [Google Scholar]
- Y. Gu, J. Pei, S. Yuan, W. Wang, F. Zhang, P. Wang, D. Appiah, Y. Liu, Clocking effect of vaned diffuser on hydraulic performance of high-power pump by using the numerical flow loss visualization method, Energy 170, 986–997 (2019) [CrossRef] [Google Scholar]
- B. Yang, B. Li, H. Chen, Z. Liu, Entropy production analysis for the clocking effect between inducer and impeller in a high-speed centrifugal pump, Proc. Inst. Mech. Eng. C 233, 5302–5315 (2019) [Google Scholar]
- Q. Deng, J. Pei, W. Wang, B. Lin, C. Zhang, J. Zhao, Energy loss and radial force variation caused by impeller trimming in a double-suction centrifugal pump, Entropy 23 (2021) [Google Scholar]
- H. Chang, W. Shi, W. Li, J. Liu, Energy loss analysis of novel self-priming pump based on the entropy production theory, J. Thermal Sci. 28, 306-318 (2018) [Google Scholar]
- L. Ji, W. Li, W. Shi, F. Tian, R. Agarwal, Effect of blade thickness on rotating stall of mixed-flow pump using entropy generation analysis, Energy 236, 121381 (2021) [CrossRef] [Google Scholar]
- B. Qian, J.P. Chen, P. Wu, D.Z. Wu, P. Yan, S.Y. Li, Investigation on inner flow quality assessment of centrifugal pump based on Euler head and entropy production analysis, IOP Conf. Ser.: Earth Environ. Sci. 240 (2019) [Google Scholar]
- H. Hou, Y. Zhang, Z. Li, A numerical research on energy loss evaluation in a centrifugal pump system based on local entropy production method, Thermal Sci. 21, 1287–1299 (2017) [CrossRef] [Google Scholar]
- X. Zhao, Z. Wang, Y. Xiao, Y. Luo, Thermodynamic analysis of energy dissipation and unsteady flow characteristic in a centrifugal dredge pump under over-load conditions, Proc. Inst. Mech. Eng. C 233, 4742–4753 (2019) [Google Scholar]
- Y. Zhang, H. Hou, C. Xu, W. He, Z. Li, Application of entropy production method to centrifugal pump energy loss evaluation, Paiguan Jixie Gongcheng Xuebao 35 (2017) [Google Scholar]
- R. Gong, H. Wang, L. Chen, D. Li, H. Zhang, X. Wei, Application of entropy production theory to hydro-turbine hydraulic analysis, Sci. China Technol. Sci. 56, 1636–1643 (2013) [CrossRef] [Google Scholar]
- D. Li, Y. Qin, Z. Zuo, H. Wang, S. Liu, X. Wei, Numerical simulation on pump transient characteristic in a model pump turbine, J. Fluids Eng. Trans. ASME 141 (2019) [Google Scholar]
- D. Li, R. Gong, H. Wang, G. Xiang, X. Wei, D. Qin, Entropy production analysis for hump characteristics of a pump turbine model, Chinese J. Mech. Eng. (Engl. Ed.) 29, 803–812 (2016) [CrossRef] [Google Scholar]
- M.M. Ghorani, M.H. Sotoude Haghighi, A. Maleki, A. Riasi, A numerical study on mechanisms of energy dissipation in a pump as turbine (PAT) using entropy generation theory, Renewable Energy 162, 1036–1053 (2020) [CrossRef] [Google Scholar]
- A. Yu, Q. Tang, H. Chen, D. Zhou, Investigations of the thermo-dynamic entropy evaluation in a hydraulic turbine under various operating conditions, Renewable Energy 180, 1026–1043 (2021) [CrossRef] [Google Scholar]
- L. Ji, W. Li, W. Shi, F. Tian, R. Agarwal, Diagnosis of internal energy characteristics of mixed-flow pump within stall region based on entropy production analysis model, Int. Commun. Heat Mass Transfer 117, 104784 (2020) [CrossRef] [Google Scholar]
- A. Mwesigye, T. Bello-Ochende, J.P. Meyer, Numerical investigation of entropy generation in a parabolic trough receiver at different concentration ratios, Energy 53, 114–127 (2013) [CrossRef] [Google Scholar]
- L. Achour, M. Specklin, I. Belaidi, S. Kouidri, Numerical assessment of the hydrodynamic behavior of a volute centrifugal pump handling emulsion, Entropy 24 (2022) [Google Scholar]
- T.S. Vieira, J.R. Siqueira, A.D. Bueno, R.E.M. Morales, V. Estevam, Analytical study of pressure losses and fluid viscosity effects on pump performance during monophase flow inside an ESP stage, J. Petrol. Sci. Eng. 127, 245–258 (2015) [CrossRef] [Google Scholar]
- F. Lai, X. Zhu, G. Li, Numerical investigation of energy loss in a centrifugal pump through kinetic energy dissipation theory, Proc. Inst. Mech. Eng. C 234, 3745-3761 (2020) [Google Scholar]
- F. Zhang, D. Appiah, F. Hong, J. Zhang, S. Yuan, K.A. Adu-Poku, X. Wei, Energy loss evaluation in a side channel pump under different wrapping angles using entropy production method, Int. Commun. Heat Mass Transfer 113, 104526 (2020) [CrossRef] [Google Scholar]
- M.A. El-Naggar, A one-dimensional flow analysis for the prediction of centrifugal pump performance characteristics, Int. J. Rotating Mach. 2013 (2013). [Google Scholar]
Cite this article as: L. Achour, M. Specklin, M. Asuaje, S. Kouidri, I. Belaidi, Energy loss analysis of volute centrifugal pump handling non-Newtonian emulsions through entropy production theory, Mechanics & Industry 25, 13 (2024)
All Tables
Pump specifications and Reynolds number ranges: large-scale pump (pump A) and scaled-down model (pump B)
All Figures
 |
Fig. 1 Calculation domains and grid. |
| In the text | |
 |
Fig. 2 CFD head of the large-size pump (a) and scaled-down pump (b), efficiency of the large-size pump (c) and scaled-down pump (d). |
| In the text | |
 |
Fig. 3 Pump torque calculated from CFD for the large-size pump (left) and scaled-down model (right) handling different emulsions versus flow rate. |
| In the text | |
 |
Fig. 4 Total entropy production of the large size pump (left) and scaled-down model (right) handling different emulsions versus flow rate. |
| In the text | |
 |
Fig. 5 Influence of the emulsion type on the entropy production in the different parts of the large-size pump (PA) and the scaled model (PB). |
| In the text | |
 |
Fig. 6 Fraction of each entropy production in the two domains of the two pumps versus the handled fluid in partial operation condition 0.5 Qbep. |
| In the text | |
 |
Fig. 7 Fraction of each entropy production in the two domains of the two pumps versus the handled fluid at design condition Qbep . |
| In the text | |
 |
Fig. 8 Fraction of each entropy production in the two domains of the two pumps when operating with water under three different operating conditions. |
| In the text | |
 |
Fig. 9 Entropy production distribution at underflow condition 0.5 Qbep. |
| In the text | |
 |
Fig. 10 Velocity distribution and streamlines on the impeller at 0.5 Qbep. |
| In the text | |
 |
Fig. 11 Entropy production distribution at design condition Qbep. |
| In the text | |
 |
Fig. 12 Entropy production distribution at overload condition1.2 Qbep. |
| In the text | |
 |
Fig. 13 Entropy production distribution (a) and the velocity streamlines (b) at overload condition 1.2 Qbep. |
| In the text | |
 |
Fig. 14 Effective viscosity profiles for 80%O–20%W emulsion versus flow rate. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.