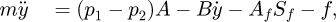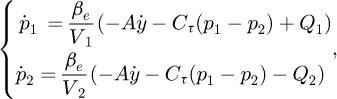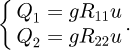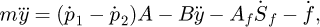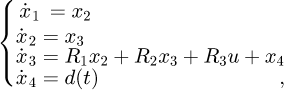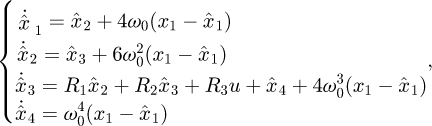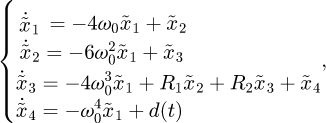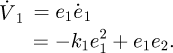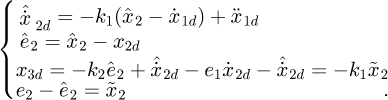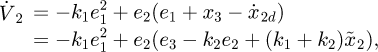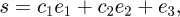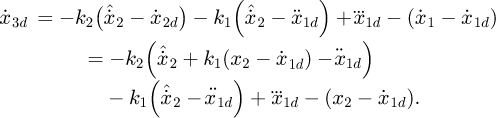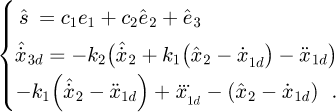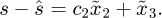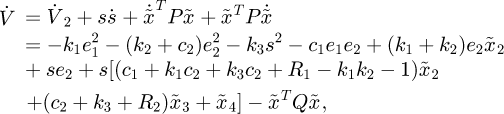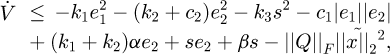| Issue |
Mechanics & Industry
Volume 25, 2024
|
|
|---|---|---|
| Article Number | 6 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/meca/2024002 | |
| Published online | 01 March 2024 | |
Regular Article
A backstepping sliding mode control algorithm of electro-hydraulic position servo system of valve-controlled symmetric cylinder based on extended state observer
Department of Electromechanical and Automobile, Chizhou Vocational and Technical College, Chizhou, 247100 China
* e-mail: 1017045679@qq.com
Received:
29
March
2023
Accepted:
12
January
2024
Electro-hydraulic position servo system of valve-controlled symmetrical cylinder (EPSSVCS) is a very important and widely used electro-hydraulic servo system, the performance of which is often affected by friction nonlinearity and external random disturbances together with unmodeled dynamic factors such as parameter uncertainty in practical work. To improve the tracking performance of the system, a backstepping sliding mode control algorithm (BSMC) based on an extended state observer was presented in this paper. Firstly, a nonlinear mathematical model of the EPSSVCS was established which takes into account the composite disturbance induced by the systematic friction nonlinearity, external disturbances and unmodeled dynamic factors. Then, an extended state observer (ESO) was designed which can effectively estimate the velocity, acceleration, and composite disturbance of the valve-controlled cylinder online. Furthermore, a kind of BSMC was presented based on the online ESO estimates and the displacement feedback signals. The control law was given and the system stability was proved. The analysis results showed that the output signal of the system can effectively track the input signal under the influence of typical external disturbances and unmodeled dynamic factors, which illustrated the effectiveness of the established nonlinear mathematical model and the stability of the designed control system. Moreover, by taking the parameters of the electro-hydraulic servo system of a certain type of CNC machine tool as a real example, the proposed algorithm (BSMC) was compared with the conventional PID control algorithm, the backstepping sliding mode control algorithm (BSC), and the adaptive robust control algorithm (ARC), and the results verified the superiority of the BSMC. This work may provide a useful reference for the research in the field of related control systems.
Key words: Electro-hydraulic position servo system / valve-controlled symmetrical cylinder / extended state observer (ESO) / backstepping sliding mode control algorithm (BSMC) / composite disturbance
© H. Chen, Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Electro-hydraulic servo system has the characteristics of strong bearing capacity, fast response speed and high control accuracy [1,2], which are widely used in various fields such as numerical control systems [3,4], vehicle hydraulic turbines [5], robots [6–8] and automobile suspensions [9]. EPSSVCS is an important type of electro-hydraulic servo system. Designing a high-quality controller is crucial, as it directly determines the rapidity and accuracy of the output signal when tracking the expected signal and hence determining the actual performance of the control system.
In recent years, many scholars have conducted a series of research on this issue by means of linear or nonlinear modeling. In the study of linear modeling, people generally viewed the system friction as purely viscous friction, ignoring the friction nonlinearity and the external random disturbances together with unmodeled dynamic factors such as parameter uncertainty. For example, Kunshan et al. [10] designed a backstepping controller based on the construction of an online linearization model in which the uncertain factors that exist in real system were not considered. To improve the tracking performance of the valve-controlled symmetrical cylinder electro-hydraulic position servo system, it is necessary to establish a nonlinear mathematical model of the electro-hydraulic servo system, laying the foundation for the design of high-performance controllers for the system. Huang et al. [11], Liu et al. [12] and Wen et al. [13] all studied a fuzzy control algorithm by constructing fuzzy disturbance observer, optimizing parameters of the system, using fuzzy disturbance observer to estimate the value of the system and designed a controller combined with a backstepping sliding mode control algorithm. Yang et al. [14] established a mathematical model of nonlinear system, optimizing the data collected of the system by using a backstepping control algorithm (BSC), however, it was more idealistic about the form of system data collection and ignored the unmodeled dynamic characteristics. Yao et al. [15] proposed a wavelet neural network system to track the output signal of valve-controlled cylinder, but the neural network system model constructed was relatively complex and had a slow convergence rate. Wang et al. [16] adopted an adaptive fuzzy PID control algorithm to control the output signal of the valve control cylinder, and the adaptive fuzzy PID controller could dynamically adjust parameters in a timely manner, although the uncertainties of the system were considered, accurate control of the system required a large amount of data and experience, otherwise the control accuracy would be affected. Yue et al. [17] and Hu et al. [18] both proposed an adaptive robust sliding mode control algorithm which combined adaptive robust control with a friction model, reduced the impact of external disturbances and system friction, improved the control accuracy and dynamic tracking performance of the electro-hydraulic position servo system, although these algorithms could suppress model parameter uncertainties and external disturbances, robust controllers had a high order. Sun et al. [19], Jing et al. [20] and Luo et al. [21] all studied an extended state adaptive observer, considered the influence of nonlinear friction factors on the dynamic and static performance of the system, reduced the error of tracking the desired signal by the output signal of the valve- controlled cylinder. Zhang et al. [22] and Du et al. [23] both proposed an adaptive sliding mode control algorithm which shortened the time to reach the sliding mode surface and reduced the chattering problem of sliding mode variable structure, by introducing exponential reaching law and power reaching law, however, it was not sensitive to the disturbance of the system and parameter changes, and needed the upper bound of the system uncertainty factors, otherwise, the system was prone to buffeting. Overall, the existing research on nonlinear models is still being deepened in order to continuously improve the control performance of electro-hydraulic servo systems.
In this paper, a new control algorithm is proposed. Firstly, a nonlinear mathematical model of the EPSSVCS is established in which the composite disturbance produced by the friction nonlinearity and external random disturbances together with unmodeled dynamic factors are embodied. Then, an ESO is designed to effectively estimate the velocity, acceleration, and the composite disturbance of the valve-controlled cylinder online. Furthermore, a kind of BSMC is presented based on the online ESO estimates and the displacement feedback signals and the control law is given. The stability proof is also provided for the control system. To verify the rationality of the nonlinear model and the algorithm, the influences of several typical external disturbances and unmodeled dynamic factors are investigated and the signal tracking ability of the system is illustrated. Moreover, the proposed algorithm (BSMC) is further compared with three kinds of existing algorithms, namely, the conventional PID control algorithm, the backstepping sliding mode control algorithm (BSC), and the adaptive robust control algorithm (ARC). The comparative results can verify the superiority of the BSMC, hence providing a beneficial reference for related researches of control systems.
The paper is organized as follows. The nonlinear mathematical model of the system is given in Section 2. The ESO and BSMC are presented in Sections 3.1 and 3.2 respectively. Section 4 gives the proof of the system stability. Section 5 conducts the analysis of several examples and Section 6 concludes the work.
2 Nonlinear mathematical model of the system
The structural diagram of the considered EPSSVCS is shown in Figure 1.
The expected signal is input to the controller, which acts on the electro-hydraulic servo valve through the servo amplifier. The hydraulic cylinder generates output signal of position under the action of electro-hydraulic servo valve and this signal is fed back to the controller by using the position sensor.
According to Newton's second law, the dynamic equation of the inertial load can be obtained as
where m and y are the load mass and displacement respectively, p1 and p2 represent the working pressure of the left and right cavities respectively, A is the effective area of the two cavities, B is the viscous friction coefficient, Af represents the Coulomb friction amplitude, Sf is the shape function of the Coulomb friction, f represents the external disturbance and unmodeled dynamics of the system.
The dynamic equation for the pressure of the two chambers of the valve controlled symmetrical cylinder is:
where βe is the oil bulk modulus, V1 = V01 + Ay and V2 = V02 − Ay represent the effective volumes of the two cavities respectively, V01 and V02 denote the initial volumes of the two cavities respectively, and Cτ represents the internal leakage coefficient, Q1 and Q2 represent the inlet and return oil flow rates of the hydraulic cylinder, respectively.
Assuming that the frequency bandwidth of the electro-hydraulic position servo system is much smaller than that of the electro-hydraulic servo valve, and the electro-hydraulic servo valve is a proportional control link, the flow equation of the electro-hydraulic servo valve can be given as
where ρ is the hydraulic oil density, Cd is the discharge coefficient for the orifice of servo valve, ki is the current gain of the servo valve spool, ω is the orifice area gradient, u is the control output, ps is the pressure source of the system and pr represents the return oil pressure.
Defining function s(u)as:
and setting  then equation (3) can be simplified as
then equation (3) can be simplified as
To facilitate the analysis of the tracking accuracy of the output signal, the dynamic equation of the inertial load, the pressure dynamic equation of the valve-controlled cylinder and the flow equation of the electro-hydraulic servo valve is combined to establish a third order differential equation that can describe the system in the following form
or
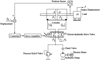 |
Fig. 1 The structural diagram of the considered EPSSVCS. |
3 Controller design
The block diagram of the proposed BSMC based on ESO is shown in Figure 2. The controller design includes two parts: (1) Building an ESO and (2) Designing a BSMC based on the ESO.
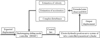 |
Fig. 2 Block diagram of the BSMC based on ESO. |
3.1 ESO design
Setting the state variable as 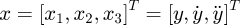 , where
, where  represent the load displacement, speed and acceleration, respectively, the state space equation of the system can be written as follows according to equation (7):
represent the load displacement, speed and acceleration, respectively, the state space equation of the system can be written as follows according to equation (7):
where the term 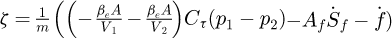 represents the composite disturbance brought by the friction nonlinearity, external disturbances and unmodeled dynamic factors, and
represents the composite disturbance brought by the friction nonlinearity, external disturbances and unmodeled dynamic factors, and 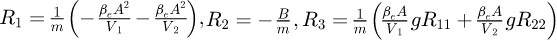
Introducing another state variable x4 as the extended state of ζ, then the state variable 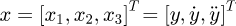 can be extended as
can be extended as  and equation (8) can be expanded as
and equation (8) can be expanded as
where d(t) represents a bounded uncertain function.
Assuming that 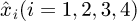 is the estimated value of the ESO for state xi, the online estimated value can be obtained as:
is the estimated value of the ESO for state xi, the online estimated value can be obtained as:
where ω0 is the bandwidth of ESO [24].
Therefore, the online estimation error 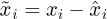 of the ESO can be expressed as
of the ESO can be expressed as
which can also be described in matrix form, i.e., 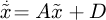 , and
, and 
The constructed ESO (Eq. (11)) can then be used to perform online observation and estimation of load speed, acceleration and composite disturbance.
3.2 BSMC based on ESO
Based on the ESO described above, a BSMC can be further designed by using the Lyapunov function and the control law can be obtained. The detailed derivation process is as follows where 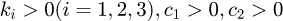 are controller parameters.
are controller parameters.
Step 1: Setting x1d as the displacement tracking value of x1, the displacement tracking error is 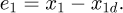 We introduce the Lyapunov function of the primary system as
We introduce the Lyapunov function of the primary system as 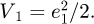 Obviously, the system is stable only when
Obviously, the system is stable only when 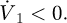 If setting
If setting 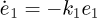 , then
, then 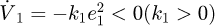 , meaning that the system is stable. We have the relation of
, meaning that the system is stable. We have the relation of  since
since 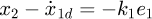 , hence the value of x2 is
, hence the value of x2 is  Furtherly, setting x2d as the displacement tracking value of x2, the displacement tracking error is
Furtherly, setting x2d as the displacement tracking value of x2, the displacement tracking error is 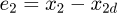 from which it can be found that:
from which it can be found that:
Step 2: To ensure that e1 and e2 in equation (12) tend to 0, a Lyapunov function of the secondary system is introduced which should include e1 and e2. The Lyapunov function is set as
From equations (12) and (13), it can be obtained that
If this secondary system is to be stable, then 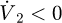 should be satisfied. Since the primary system is already stable, it is only necessary to ensure
should be satisfied. Since the primary system is already stable, it is only necessary to ensure 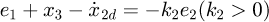 to keep the system stable. It can be seen that the tracking value of
to keep the system stable. It can be seen that the tracking value of 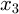 is
is  Further, by setting
Further, by setting 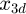 as the displacement tracking value of
as the displacement tracking value of 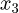 , the displacement tracking error is
, the displacement tracking error is 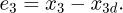 Since
Since 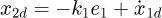 , we have
, we have 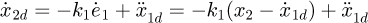 in equation (14).
in equation (14).
In the design of ESO, the variables 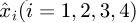 have been defined as the estimated values of state
have been defined as the estimated values of state 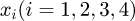 , then
, then 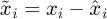 represents the error online estimated by the ESO. Hence, the following relationship can be obtained:
represents the error online estimated by the ESO. Hence, the following relationship can be obtained:
From equation (15), it can be acquired that:
and the following relation can be obtained according to equations (14)–(16):
Step 3: Defining a sliding mode function and deriving the control law of the BSMC based on ESO.
Let the sliding mode function be:
From equations (9) and (18), it is not difficult to found that:
From the first and second steps, it can be seen that
Setting 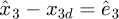 , equations (18) and (20) can be transformed as:
, equations (18) and (20) can be transformed as:
According to equations (19)–(21), the control law u of the BSMC based on ESO is acquired as following where  is used:
is used:
4 Stability proof of the system
Defining  , following equation can be obtained according to equations (18)–(21):
, following equation can be obtained according to equations (18)–(21):
According to equations (17), (22) and (23), it can be found that:
Setting the Lyapunov function as
and taking the derivative of V, and then substituting equations (17), (18) and (24) into equation (25), we have
where 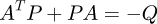 and P is a real symmetric positive definite matrix.
and P is a real symmetric positive definite matrix.
By setting 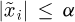 , we have
, we have
where 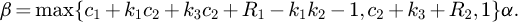
According to the Young's inequality  , it is easy to found that
, it is easy to found that
where 
If the selected control parameters satisfy  , then all signals of the valve controlled symmetrical cylinder electro-hydraulic position servo system are consistent and ultimately bounded, and the tracking error of the system can be arbitrarily small by adjusting the parameters
, then all signals of the valve controlled symmetrical cylinder electro-hydraulic position servo system are consistent and ultimately bounded, and the tracking error of the system can be arbitrarily small by adjusting the parameters 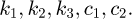
5 Example analysis and performance comparison
To investigate the effectiveness of the constructed nonlinear model and control algorithm, the signal tracking performances of the system under five typical external disturbances and unmodeled dynamic factors are first analyzed where the input signal is set as  , and f is taken as sine function, unit step function, unit ramp function, unit pulse function and unit parabolic function, respectively. The analysis results are shown in Figure 3.
, and f is taken as sine function, unit step function, unit ramp function, unit pulse function and unit parabolic function, respectively. The analysis results are shown in Figure 3.
Figure 3a corresponds to the case of 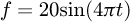 , and it can be seen that the signal tracking performance is the best. The maximum displacement of the output signal is 1.993e-01m and the relative error of the output signal to the input signal is 0.05% only. Figures 3b and 3d present the cases of unit step signal and unit pulse signal, respectively. The maximum displacement of the output signal is 2.004e-01m and 1.999e-01m respectively from which the relative errors are obtained as both 0.35%. Figure 3c is for the case of unit slope signal and the maximum displacement is found to be 2.033e-01m with an error of 1.8% relative to the input signal. The case of unit parabolic signal is shown in Figure 3e with a maximum displacement of 2.044e-01m and relative error of 2.6%. These analysis results show that under the influences of typical external disturbances and unmodeled dynamic factors, the output signal of the system can still effectively track the input signal with small errors which verifies the rationality of the nonlinear model and the control system.
, and it can be seen that the signal tracking performance is the best. The maximum displacement of the output signal is 1.993e-01m and the relative error of the output signal to the input signal is 0.05% only. Figures 3b and 3d present the cases of unit step signal and unit pulse signal, respectively. The maximum displacement of the output signal is 2.004e-01m and 1.999e-01m respectively from which the relative errors are obtained as both 0.35%. Figure 3c is for the case of unit slope signal and the maximum displacement is found to be 2.033e-01m with an error of 1.8% relative to the input signal. The case of unit parabolic signal is shown in Figure 3e with a maximum displacement of 2.044e-01m and relative error of 2.6%. These analysis results show that under the influences of typical external disturbances and unmodeled dynamic factors, the output signal of the system can still effectively track the input signal with small errors which verifies the rationality of the nonlinear model and the control system.
To further illustrate the effectiveness of the proposed algorithm, the electro-hydraulic servo system of a certain type of CNC machine tool is considered here as an example and the related parameters are shown in Table 1. The proposed algorithm (BSMC) is analyzed and calculated, and compared with existing three algorithms, namely, conventional PID control algorithm, backstepping control algorithm (BSC), and adaptive robust control algorithm (ARC). In the example analysis, the coulomb friction shape function  and coulomb friction amplitude Af = 10 are adopted, and the external disturbance of the system and unmodeled dynamics are set as an equivalent composite disturbance
and coulomb friction amplitude Af = 10 are adopted, and the external disturbance of the system and unmodeled dynamics are set as an equivalent composite disturbance  for illustration. Furthermore, the expected displacement signal is set as
for illustration. Furthermore, the expected displacement signal is set as 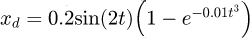 and the simulation step size is taken as 0.0002s.
and the simulation step size is taken as 0.0002s.
The tuning process and results of relevant parameters of the controller are as follows:
For the proposed control algorithm (BSMC): ESO Bandwidth is set as ω0 = 100 [24] and the selection of the controller parameters can refer to Section 4, which means that
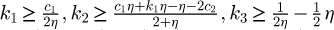 should be satisfied and the system tracking error is tuned to be rather small by adjusting
should be satisfied and the system tracking error is tuned to be rather small by adjusting  Accordingly, the controller parameters are finally set as
Accordingly, the controller parameters are finally set as 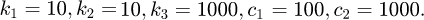
For the conventional PID control algorithm [1]: The parameter selection of PID control algorithm is based on the trial debugging of the output displacement signal. The trial debugging is conducted from a smaller value. kp is adjusted firstly to reduce the error to appropriate value and ki is tuned further to eliminate the error, and kd is adjusted finally to reduce the overshoot and oscillation, hence enhancing the stability and the dynamic performance of the system. By comprehensively balancing the transient response and steady-state performance of the system, the controller parameters are finally determined through debugging as
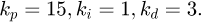
For the Backstepping Sliding Mode Control Algorithm (BSC) [25]: According to equation (7), it is set that
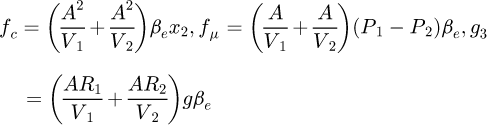
 The control law of BSC is
The control law of BSC is  The parameters (k1,k2 and (k3) should be selected to meet the system stability requirements. By consideration of the transient and steady-state performance of the system, the control parameters are finally set as
The parameters (k1,k2 and (k3) should be selected to meet the system stability requirements. By consideration of the transient and steady-state performance of the system, the control parameters are finally set as 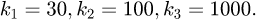
For the Adaptive Robust Control Algorithm (ARC) [17]: According to equation (7), it is set that
 ,
, 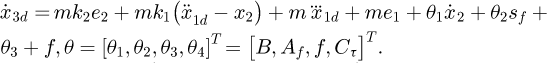 The control law of ARC is
The control law of ARC is 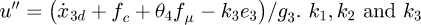 k1,k2 and k3 should be also selected to meet the stability requirements. Similarly, they are finally set as
k1,k2 and k3 should be also selected to meet the stability requirements. Similarly, they are finally set as 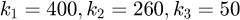 by tuning the system responses.
by tuning the system responses.
The displacement errors of four algorithms are calculated and the results are depicted in Figure 4. It can be clearly seen that BSMC and ARC have smaller displacement errors which are -1.027e-04 and -2.261e-04 respectively, compared with BSC(-3.266e-04) and conventional PID control algorithm (-6.050e-02).
The displacement tracking performance of the four algorithms are compared as shown in Figure 5.
The results show that all of the four algorithms have good tracking effect within the period of t < 5s. However, when t > 5s, the conventional PID control algorithm exhibits the worst tracking effect with slow time response and low accuracy in tracking displacement while BSMC and ARC possess much better tracking performance. Moreover, the tracking displacement curve of BSMC coincides with the expected displacement curve with higher accuracy, compared with ARC and BSC which are slightly overshoot.
The control law u response curves of four algorithms are shown in Figure 6 from which it is observed that BSMC can still ensure stable output with fast time response under composite disturbance. Figures 7–9 show the velocity, acceleration and composite disturbance estimations of valve-controlled cylinder by using the designed ESO. It can be seen that the overall estimation effect is rather good and the estimated values are bounded.
To evaluate the effectiveness of BSMC more clearly, three performance indexes are selected here for comparison, namely the maximum tracking displacement error (Max), the average tracking displacement error (Mean) and the standard deviation of tracking displacement error (Rms), as listed in Table 2.
It is found from Table 2 that the maximum tracking error of BSMC is the smallest one (1.030e-04) and the accuracy enhancements relative to ARC and BSC achieve 54.75% and 68.28% respectively. Due to the disability to compensate for composite disturbance in the forward feedback channel, the PID control algorithm has the largest tracking displacement error compared to others.
The average value of tracking displacement error reflects the average level of control error. The results show that the average level of BSMC is also the best one followed by ARC and the PID control is the worst one. The standard deviation of tracking displacement error reflects the degree of dispersion of control error. Similarly, it can be found that the degree of dispersion of BSMC is the smallest one followed by ARC, and the PID control is the largest one.
 |
Fig. 3 Tracking performance of system signals under five typical external disturbances and unmodeled dynamic factors: (a)∼(e) corresponds to the case of sine function, unit step function, unit ramp function, unit pulse function and unit parabolic function, respectively. |
 |
Fig. 3 (Continued). |
 |
Fig. 3 (Continued). |
Relevant parameters of electrohydraulic servo system of a certain type of CNC machine tool.
 |
Fig. 4 Displacement error of four control algorithms. |
 |
Fig. 5 Displacement tracking performance comparison of the four algorithms. |
 |
Fig. 6 The control law u response curves of four control algorithms. |
 |
Fig. 7 Velocity and the estimation of velocity. |
 |
Fig. 8 Acceleration and the estimation of acceleration. |
 |
Fig. 9 Estimation of the composite disturbance |
Performance indexes of four algorithms.
6 Conclusions
In this paper, a backstepping sliding mode control algorithm (BSMC) based on ESO is proposed for the EPSSVCS with composite disturbance induced by friction nonlinearity and external disturbances together with unmodeled dynamic factors. An ESO is designed to effectively estimate the velocity, acceleration and the composite disturbance of the valve-controlled cylinder online. A kind of BSMC is presented based on the online ESO estimates and the displacement feedback signals, the control law is given and the system stability is proved. Through case studies, the proposed nonlinear model and algorithm are found to be effective and the advantage of BSMC is also shown by comparison with other algorithms. The main results are as follows:
Under the influence of typical external disturbances and unmodeled dynamic factors, the output signal of the system can still effectively track the input signal, and the error of the output signal relative to the input signal remains small, which shows the effectiveness of the established nonlinear model and the correctness of the designed control system.
The designed ESO shows good tracking performance and can effectively estimate the values of velocity, acceleration and composite disturbances online, which not only illustrates the stability of the system and may also provide certain reference for the measurements of velocity, acceleration and composite disturbances that are difficult to measure in practical engineering fields.
The presented algorithm has smaller tracking displacement error, higher control accuracy and smaller dispersion compared to PID algorithm, BSC and ARC. The control accuracy of BSMC has been improved by 54.75% and 68.28% respectively by comparison with ARC and BSC, hence providing a feasible way for the design of EPSSVCS and related control systems.
Funding
This work was supported by Support Project for Outstanding Young Talents in Colleges and Universities in Anhui Province (Project No. gxyq2021273) and Key Project for Natural Science Research colleges and universities in Anhui Province (Project No. 2023AH053227, Project No. 2022AH052868).
Conflict of interest
The author declared no potential conflicts of interest with respect to the research, authorship, and/or publication of this article.
Author contribution statement
This article is a sole author, and the entire content is written by the author personally.
References
- T. Samakwong et al., PID controller design for electro-hydraulic servo valve system with genetic algorithm[J], Procedia Comput. Sci. 86, 91–94 (2016) [CrossRef] [Google Scholar]
- Y. Ma et al., Research on control strategy of asymmetric electro-hydraulic servo system based on improved PSO algorithm[J], Adv. Mech. Eng. 14, 1–14 (2022) [Google Scholar]
- R.S. Kumar et al., Adaptive control systems in CNC machining processes-A review[J], Adv. Nat. Appl. Sci. 10, 120–129 (2016) [Google Scholar]
- J. Guo et al., Research on CNC machining technology of the upper shell of electro-hydraulic servo valve[J], J. Phys.: .: Conf.Ser. 1635, 012016 (2020) [CrossRef] [Google Scholar]
- B. Gao et al., Research on position/velocity synergistic control of electro hydraulic servo system[J], Recent Pat. Mech. Eng. 13, 366–377 (2020) [CrossRef] [Google Scholar]
- Yuan et al., Application of multi-objective controller to optimal tuning of PID gains for a hydraulic turbine regulating system using adaptive grid particle swam optimization[J], ISA Trans. 56, 173–187 (2015) [CrossRef] [Google Scholar]
- Z. Dan et al., A review on model reference adaptive control of robotic manipulators[J], Annu. Rev. Control 43, 188–198 (2017) [CrossRef] [Google Scholar]
- Shao et al., Recent advances on gait control strategies for hydraulic quadruped robot[J], Recent Pat. Mech. Eng. 1, 15–23 (2018) [CrossRef] [Google Scholar]
- Yingbo et al., Approximation-free control for vehicle active suspensions with hydraulic actuator[J], IEEE Trans. Ind. Electron. 65, 7258–7267 (2018) [CrossRef] [Google Scholar]
- K. Jin et al., Linear active disturbance rejection control for the electro-hydraulic position servo system[J], Sci. Prog. 104, 1–30 (2021) [Google Scholar]
- X. Huang et al., Indirect adaptive fuzzy sliding-mode control for hydraulic manipulators[J], Adv. Mech. Des. 77, 229–242 (2020) [Google Scholar]
- B.Q. Liu et al., Modeling and robust adaptive fuzzy control for servo layer control of a motor/gear subsystem[C], Proc. IEEE Int. Symp. Ind. Electron. 82, 1835–1840 (2019) [Google Scholar]
- Y. Wen et al., Research on fuzzy symmetrical control of valve controlled asymmetric hydraulic cylinder system[J], J. Intell. Fuzzy Syst. 41, 4451–4460 (2021) [CrossRef] [Google Scholar]
- A. Gy et al., Nonlinear adaptive output feedback robust control of hydraulic actuators with largely unknown modeling uncertainties[J], Appl. Math. Modell. 79, 824–842 (2020) [CrossRef] [Google Scholar]
- Zhikai et al., Model reference adaptive tracking control for hydraulic servo systems with nonlinear neural-networks[J], ISA Trans. 100, 396–404 (2019) [Google Scholar]
- Y. Wang et al., Adaptive fuzzy PID control of hydraulic servo control system for large axial flow compressor[J], IOP Conf. Ser.: Mater. Sci. Eng. 231, 012086 (5pp) (2017) [CrossRef] [Google Scholar]
- F. Yue, et al., Robust adaptive integral backstepping control for opto-electronic tracking system based on modified Lu Gre friction model[J], ISA Trans. 80, 312–321 2018 [CrossRef] [Google Scholar]
- J. Hu et al., High-accuracy robust adaptive motion control of a torque-controlled motor servo system with friction compensation based on neural network[C], Proc. Inst. Mech. Eng., Part C: J. Mech. Eng. Sci. 233, 2318–2328 (2019) [CrossRef] [Google Scholar]
- C. Sun et al., Sliding mode control of electro-hydraulic position servo system based on adaptive reaching, Appl. Sci. 12, 6897 (2022) [CrossRef] [Google Scholar]
- Jing et al., Adaptive extended state observer-based flatness nonlinear output control for torque tracking of electrohydraulic loading system[J], Trans. Inst. Meas. Control 40, 2999–3009 (2018) [CrossRef] [Google Scholar]
- C. Luo et al., Extended-state-observer-based output feedback adaptive control of hydraulic system with continuous friction compensation[J], J. Franklin Inst. 356, 8414–8437 (2019) [CrossRef] [MathSciNet] [Google Scholar]
- Xiaofei et al., An adaptive sliding mode controller with the exponential and power reaching law for discrete systems[C], Proceedings of 2018 37th Chinese Control Conference (CCC), Piscataway: IEEE 114, 2711–2716 (2018) [Google Scholar]
- Y. Du et al., Frequency-domain system identification of an unmanned helicopter based on an adaptive genetic algorithm[J], IEEE Trans. Ind. Electron. 61, 870–881 (2014) [CrossRef] [Google Scholar]
- Z. Gao, Scaling and bandwidth-parameterization based controller tuning[J], Proc. Am. Control Conf. 6, 4989–4996 (2003) [Google Scholar]
- S. Zhang, T. Chen, Adaptive backstepping sliding mode control for direct driven hydraulics[J], MDPI 64, 1 (2020) [Google Scholar]
Cite this article as: H. Chen, A backstepping sliding mode control algorithm of electro-hydraulic position servo system of valve-controlled symmetric cylinder based on extended state observer, Mechanics & Industry 25, 6 (2024)
All Tables
Relevant parameters of electrohydraulic servo system of a certain type of CNC machine tool.
All Figures
 |
Fig. 1 The structural diagram of the considered EPSSVCS. |
| In the text | |
 |
Fig. 2 Block diagram of the BSMC based on ESO. |
| In the text | |
 |
Fig. 3 Tracking performance of system signals under five typical external disturbances and unmodeled dynamic factors: (a)∼(e) corresponds to the case of sine function, unit step function, unit ramp function, unit pulse function and unit parabolic function, respectively. |
| In the text | |
 |
Fig. 3 (Continued). |
| In the text | |
 |
Fig. 3 (Continued). |
| In the text | |
 |
Fig. 4 Displacement error of four control algorithms. |
| In the text | |
 |
Fig. 5 Displacement tracking performance comparison of the four algorithms. |
| In the text | |
 |
Fig. 6 The control law u response curves of four control algorithms. |
| In the text | |
 |
Fig. 7 Velocity and the estimation of velocity. |
| In the text | |
 |
Fig. 8 Acceleration and the estimation of acceleration. |
| In the text | |
 |
Fig. 9 Estimation of the composite disturbance |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.