| Issue |
Mechanics & Industry
Volume 21, Number 1, 2020
|
|
|---|---|---|
| Article Number | 104 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/meca/2019072 | |
| Published online | 07 January 2020 | |
Regular Article
Friction and wear analysis of the external return spherical bearing pair of axial piston pump/motor
1
School of Mechanical Engineering, Anhui University of Science and Technology, Huainan, Anhui 232001, PR China
2
Anhui Key Laboratory of Mine Intelligent Equipment and Technology, Anhui University of Science and Technology, Huainan 232001, PR China
3
State Key Laboratory Mining Response and Disaster Prevention and Control in Deep Coal Mines, Anhui University of Science and Technology, Huainan 232001, PR China
* e-mail: dhs1998@163.com
Received:
8
May
2019
Accepted:
26
September
2019
By discretizing the contact area between the external retainer plate and the external spherical hinge, a mathematical model for the force relation of an arbitrary contact point in the external return spherical bearing pair was established and a mathematical expression for the friction power of the external return spherical bearing pair was deduced. The influences of the slant inclination of the external swash plate, pump shaft rotating speed, eccentricity, spring force and number of discrete contact points on the friction power were also analysed. The results show that the power fluctuation amplitude of the discrete contact point in the external return spherical bearing pair increases with increasing slant inclination of the external swash plate, pump shaft rotating speed and spring force; the total friction power was found to increase linearly. However, the power fluctuation amplitude of the discrete contact point in the external return spherical bearing pair was found to decrease with increasing eccentricity, with the total friction power decreasing nonlinearly until reaching a certain value. The distribution shape of the friction power of the discrete contact point is only affected by eccentricity. If the eccentricity is large, the friction power of the discrete point presents a double-peak distribution, whereas if it is small, a multiple-peak distribution is observed.
Key words: Axial piston pump/motor / external return mechanism / friction power / normal force / spherical bearing pair
© AFM, EDP Sciences 2019
1 Introduction
Axial piston pump/motor are important components that are widely used for industrial applications in the hydraulic field. Such components have several advantages including small volume, high efficiency and smooth operation [1–4]. Three key friction pairs consisting of the plunger–cylinder block, the slipper–swash plate and the cylinder block–port plate have a great influence on the service life and performance of pump/motor. Researchers worldwide have dedicated great attention to this, achieving fruitful results [5–7]. Rokala et al. investigated the influence of the slant inclination of the external swash plate on the water-film thickness of the slipper pair of the hydraulic axial piston pump [8]. Zhang et al. investigated the influence of slipper rotation on the dynamic and lubrication characteristics of the slipper of the axial piston pump and built a test bench to verify the correctness of the theory [9]. Li et al. textured the port pair by photolithography and electrolysis and studied the friction and wear performance of the port pair on a testing machine [10]. Jeong et al. and Vatheuer et al. analysed the kinematic relation of the plunger in the plunger holes and established a mathematical model for the instantaneous friction force of the plunger pair and the average torque loss [11,12]. Lin et al. established a dynamic friction model for the slipper pair and analysed the effects of pump shaft rotating speed, load force and oil viscidity on the performance of the slipper [13].
However, only little research has been performed on the friction pair of the retainer plate-spherical hinge. The friction loss of the return mechanism determines the stability of oil absorption of the plunger pump/motor. So, it is necessary to perform a thorough research on the friction pair of the retainer plate-spherical hinge. Manring et al. established a mathematical model for the relative motion of the retainer plate and the spherical hinge and analysed the relationship between slant inclination of the swash plate and relative motion velocity [14]. Sun et al. studied the force relation between the retainer plate and the spherical hinge, and calculated the friction-power consumption between them. Then, they built a test bench for the friction-power consumption of the retainer plate and the spherical hinge and verified the correctness of the theoretical analysis [15,16]. Xu et al. established a mathematical model for the relative motion relation between the retainer plate and the spherical hinge, and built a virtual prototype model of the solid–liquid coupling of the plunger pump to simulate their relative motion. Virtual prototype models can consider the interactions between the components and calculate the influence of the dynamic performance of each component on reaching the target in real time [17,18]. Wang et al. established an analytical method for determining the oil-film-lubrication value of the return spherical bearing pair by extending the classical Jakobsson–Floberg–Olsson (JFO) cavitation algorithm and considering the influence factor of the shear velocity on a complex surface [19].
The external return mechanism is an indispensable key component of the balanced double-row axial piston pump and dual-drive axial piston motor [20,21]. The working principle of the external return mechanism is similar to the common return mechanism. It has several advantages including a large pressing force and a compact structure. Thus, it can also be used for normal axial piston pump/motor. The external return mechanism is an important intermediate structure of the balanced double-row axial piston pump and dual-drive axial piston motor [22]. Its kinematic and friction-lubricating characteristics have a great influence on the working performance of the slipper pair, plunger pair and port pair of the pump/motor—and they are also a key factor affecting technical indicators such as service life, working performance and vibration noise of the pump/motor component. Deng et al. carried out a deep analysis of the kinetic characteristics of the external return mechanism [23]. This paper will further analyse the force laws and wear characteristics of the external return mechanism and provide a basis for a dynamic-pressure lubrication-characteristics analysis.
2 Working principle of the external return spherical bearing pair
The main structure of the balanced double-row axial piston pump is shown in Figure 1. As an indispensable key component of the balanced double-row axial piston pump, the external return mechanism mainly includes an external spherical hinge, an external retainer plate, a juncture, compression springs and spring seats. In addition, it's working principle is similar to the common return mechanism. The common axial piston pump forms the spherical bearing pair by matching the inner contour surface (cone surface) of the retainer plate and the outer contour surface (spherical surface) of the spherical hinge. On the other hand, the external return mechanism forms the spherical bearing pair by matching the outer contour surface (arc surface) of the retainer plate and the inner contour surface (spherical surface) of the external spherical hinge. Through the spring that is evenly distributed around the outer surface of the cylinder block provides compression force for the external spherical hinge, the external slipper is pressed against the surface of the external retainer plate. Since the compression spring is always in a state of compression and has no reciprocating motion, the fatigue loss of the spring will be lower and the working life can be prolonged. This further increases the reliability of the axial piston pump.
 |
Fig. 1 Structure of the balanced double-row axial piston pump. 1. Slipper; 2. Internal swash plate; 3. Internal spherical hinge; 4. Pump shaft; 5. Front end cover; 6. External swash plate; 7. External spherical hinge; 8. Shell; 9. External retainer plate; 10. Juncture. 11. Spring seat; 12. Compression spring; 13. Plunger; 14. Valve plate; 15. Rear end cover. |
3 Force analysis of the external return spherical bearing pair
The force between the external retainer plate and the external spherical hinge is shown in Figure 2a. Due to the relative motion between the external retainer plate and the external spherical hinge, at the contact point, the external spherical hinge is acted upon not only by the normal force N of the external retainer plate but also by its sliding friction force Ff. The external retainer plate and the external spherical hinge show a complicated relation of space motion. To study the wear characteristics of the external return spherical bearing pair, the contact area between the external retainer plate and the external spherical hinge is discretized, and the effects of parameters such as slant inclination of the external swash plate, pump shaft rotating speed, eccentricity and spring force on the friction power of every contact point are analysed.
For the convenience of analysis, we discretize the contact area between the external retainer plate and the external spherical hinge into m contact points that are uniformly distributed. A certain contact point m1 is chosen to force analysis, as shown in Figure 2b. The contact point m1 is acted upon by the normal force N1 of the external retainer plate and by its sliding friction force Ff1. By decomposing the normal force N1 and sliding friction force Ff1 along the x and y axes respectively, the component forces (N1 x, N1 y, Ff1 x and Ff1 y) of the normal force N1 and the sliding friction force Ff1 along the x and y axes can be obtained. The direction of the normal force N1 points to the sphere centre of the external spherical hinge, which is the same direction as that of the radius vector of the contact point m1. The sliding friction force Ff1 acts in the direction opposite to the instantaneous motion at that contact point. Since the relative motion relation in the external return spherical bearing pair is expressed in a vector equation, the force relation of an arbitrary contact point in the external return spherical bearing pair can be obtained.
At an arbitrary contact point of the external return spherical bearing pair, the normal force N1 and the sliding friction force Ff1 that acts upon the external spherical hinge can be decomposed along the i, j and k directions (i, j and k are the unit vectors of the x, y, and z axes, respectively), that is, component forces of an arbitrary contact point in these three directions are obtained. In the x direction, the external spherical hinge is only acted upon by the spring force Fsz. So, adding the component forces of these contact points along the x axis gives the balanced equation: (1)
(1)
Since the unit vector nt has the same direction as the radius vector ρ5t of the contact point mt, and the unit vector ut has a direction opposite to the relative motion velocity ΔVt of the contact point mt [23], the unit vector nt and ut can be expressed as (2)
(2)
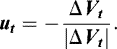 (3)
(3)
So Nt
nt represents the normal force of an arbitrary contact point mt in the external return spherical bearing pair; (Nt
nt)i represents the x component of the normal force at the contact point mt; Fft
ut represents the sliding friction force of the contact point mt; (Fft
ut)i represents the x component of the sliding friction force at the contact point mt. Thus, equation (1) can be rewritten as: (4)
(4)
If the coefficient of the sliding friction between the external retainer plate and the external spherical hinge is given by fs, equation (4) can be expressed as: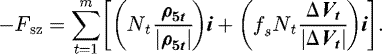 (5)
(5)
The contact point m1 at α = 0° is chosen as the reference point. Then, the components of the normal force and the sliding friction force along the x axis can be written as: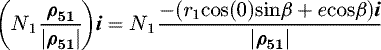 (6)
(6)
 (7)
(7)
The contact area between the external retainer plate and the external spherical hinge is discretized into m contact points that are uniformly distributed. Each contact point is related to angle α, which corresponds to the relative motion trajectories of the external return spherical bearing pair. The contact point m1 at α = 0° is chosen as the reference contact point. Then, the values of angle α corresponding to the contact points adjacent to contact point m1 are 2π/m, 4π/m, 6π/m,…, (m–1)2π/m. The normal force of each contact point is proportional to the component of the radius vector at that point along the x axis. So the normal force N2 of the second contact point m2 adjacent to the reference contact point, can be expressed as: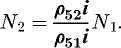 (8)
(8)
The component of the normal force N2 along the x axis can be written as: (9)
(9)
Similarly, at the contact point m2 adjacent to the reference contact point, the component of the normal force N2 and the sliding friction force Ff2 along the x axis can be written as: (10)
(10)
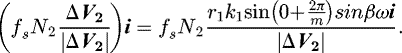 (11)
(11)
Substituting equation (8) into equation (11), we obtain equation (12), as follows: (12)
(12)
Similarly, the normal force N3 of the third contact point can be expressed as: (13)
(13)
By analogy, the component of the normal force Nm of the contact point mm along the x axis can be written as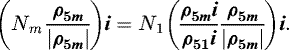 (14)
(14)
The component of the sliding friction force Ffm of the contact point mm along the x axis can be expressed as: (15)
(15)
By substituting equations (6)–(15) into equation (5), the force balance equation of the external retainer plate and the external spherical hinge in the x axis can be obtained: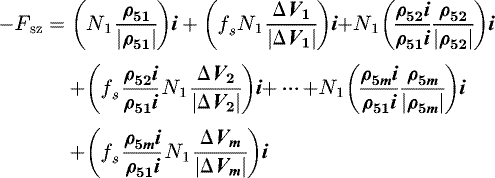 (16)
(16)
The vector equation ρ5 and the relative motion velocity vector equation ΔV of the contact point in the external return spherical bearing pair are given in reference [21]. Thus, we obtain equation (17):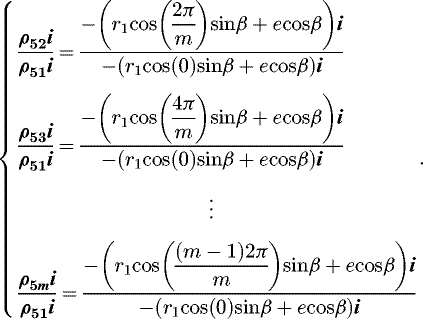 (17)
(17)
The normal force N1 on the external spherical hinge can be obtained by substituting equation (17) into equation (16). On the basis of the relation 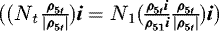 between the normal force of the adjacent contact point and N1, the normal force of all the contact points in the external return spherical bearing pair can be obtained. Based on the deduced formulas, we come to the following conclusions:
between the normal force of the adjacent contact point and N1, the normal force of all the contact points in the external return spherical bearing pair can be obtained. Based on the deduced formulas, we come to the following conclusions:
The amount of normal force Nt depends not only on the spring force Fsz and the coefficient of sliding friction fs, but also on the ratio  between the radius vector along the x axis of each discrete point and that of the reference point. But the size of the radius vector ρ5t at the discrete contact point mt is related to the slant inclination of the external swash plate β, the eccentricity e and the radius of external retainer plate r1. So, the spring force, slant inclination of the external swash plate, eccentricity and coefficient of sliding friction between the external retainer plate and the external spherical hinge are the main parameters that influence the amount of the force acting on the discrete contact point in the external return spherical bearing pair.
between the radius vector along the x axis of each discrete point and that of the reference point. But the size of the radius vector ρ5t at the discrete contact point mt is related to the slant inclination of the external swash plate β, the eccentricity e and the radius of external retainer plate r1. So, the spring force, slant inclination of the external swash plate, eccentricity and coefficient of sliding friction between the external retainer plate and the external spherical hinge are the main parameters that influence the amount of the force acting on the discrete contact point in the external return spherical bearing pair.
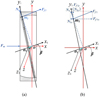 |
Fig. 2 External spherical hinge force analysis. |
4 Friction power between external retainer plate and external spherical hinge
By combining the known normal force Nt at each contact point mt between the external retainer plate and the external spherical hinge and the vector equation ΔV of relative motion velocity between the external retainer plate and the external spherical hinge, the total friction power of the contact trajectories between the external retainer plate and the external spherical hinge can be expressed as: (18)
(18)
In equation (18), the value of |ΔVt| depends on the values of parameters such as the slant inclination of the external swash plate β, pump shaft rotating speed ω and eccentricity e. The above formulas show that the magnitude of the force acting on the discrete contact point mt depends on the spring force, slant inclination of the external swash plate, coefficient of sliding friction in the external return spherical bearing pair and number of discrete contact points. So, the main parameters of influencing friction power consumption of the contact point in the external return spherical bearing pair are spring force, slant inclination of the external swash plate, pump shaft rotating speed, eccentricity, coefficient of sliding friction in the external return spherical bearing pair and number of discrete contact points. Based on the above analysis, a power simulation and analysis of the discrete contact point with different parameters is established, as shown in Table 1.
Parameters of the numerical simulation.
5 Results and analysis
5.1 Influence of the slant inclination of the external swash plate on the friction power
Figure 3 describes the influence of the external swash plate inclination on the friction power of the discrete contact point in the external return spherical bearing pair. Tables 2 and 3 describe the friction power peak-to-valley value of the discrete contact point under different external swash plate inclinations. Figure 3 and Tables 2 and 3 show that upon increasing the external swash plate inclination, the power fluctuation amplitude and the total friction power of the discrete contact point in the external return spherical bearing pair increase too. The discrete contact point of maximum power is located at different pump shaft rotation angle positions. The friction power of the discrete contact point presents phenomenon of double-peak-value in the same cycle, and the fluctuation curve is symmetrical at 180°. At pump shaft rotation angles of 0° and 180° (top and bottom dead centre positions of the external pump piston), the relative motion velocity is 0 and the friction power is 0.
 |
Fig. 3 Influence of external swash plate inclinations on the friction power of the contact point. |
Friction power peak-to-valley value of a contact point under different external swash plate inclinations (m = 721).
Friction power peak-to-valley value of a contact point under different external swash plate inclinations (m = 72 001).
5.2 Influence of the pump shaft rotating speed on the friction power
Figure 4 describes the influence of the pump shaft rotating speeds on the friction power of the discrete contact point in the external return spherical bearing pair. Tables 4 and 5 show the friction-power peak-to-valley values for the discrete contact point under different pump shaft rotating speeds. Figure 4 and Tables 4 and 5 show that upon increasing the pump shaft rotating speeds, the power fluctuation amplitude and the total friction power of the discrete contact point in the external return spherical bearing pair increase accordingly. The maximum power of the discrete contact point is located at the same pump shaft rotation angle position under different pump shaft rotating speeds. The friction power of the discrete contact point presents phenomenon of double-peak-value in the same cycle, and the fluctuation curve is symmetrical at 180°. At pump shaft rotation angles of 0° and 180°, the friction power is 0.
 |
Fig. 4 Influence of the pump shaft rotating speeds on the friction power of the contact point. |
Contact point friction power peak-to-valley value at different pump shaft rotating speeds (m = 721).
Contact point friction power peak-to-valley value at different pump shaft rotating speeds (m = 72 001).
5.3 Influence of eccentricity on the friction power
Figure 5 describes the influence of eccentricity on the friction power of the discrete contact point in the external return spherical bearing pair. Tables 6 and 7 show the friction power peak-to-valley values of the discrete contact point at different eccentricities. Figure 5 and Tables 6 and 7 show that upon increasing the eccentricity, the power fluctuation amplitude and the total friction power of the discrete contact point in the external return spherical bearing pair decrease accordingly. If the eccentricity is 15–20 mm, the power fluctuation amplitudes of the discrete contact point in the external return spherical bearing pair are similar, and no obvious changes in total friction are observed. Under different eccentricities, the maximum power of the discrete contact point is located at the different pump shaft rotation angle positions. The friction power of the discrete contact point presents phenomenon of multiple-peak-value in the same cycle, and the fluctuation curve is symmetrical at 180°. At pump shaft rotation angles of 0° and 180°, the friction power is 0.
 |
Fig. 5 Influence of eccentricity on the friction power of the contact point. |
Contact point frictional power peak-to-valley value at different eccentricities (m = 721).
Contact point frictional power peak-to-valley value at different eccentricities (m = 72 001).
5.4 Influence of the spring force on the friction power
Figure 6 describes the influence of the spring force on the friction power of the discrete contact point in the external return spherical bearing pair. Tables 8 and 9 show friction-power peak-to-valley values of the discrete contact point under different spring forces. Figure 6 and Tables 8 and 9 show that upon increasing the spring force, the power fluctuation amplitude and the total friction power of the discrete contact point in the external return spherical bearing pair increase accordingly. The maximum power of the discrete contact point is located at the same pump shaft rotation angle position under different spring forces. Friction power of the discrete contact point presents phenomenon of double-peak-value in the same cycle, and the fluctuation curve is symmetrical at 180°. At pump shaft rotation angles of 0° and 180°, the friction power is 0.
 |
Fig. 6 Influence of the spring forces on the friction power of the contact point. |
Contact point friction power peak-to-valley value under different spring force (m = 721).
Contact point friction power peak-to-valley value under different spring force (m = 72 001).
5.5 Overall influence of the structural parameters on the friction power
Figure 7 shows a comparison of the amplitude changes of the friction power that occur at discrete contact point under different parameters of the external return mechanism, such as slant inclination of the external swash plate, pump shaft rotating speed, eccentricity and spring force. As shown in Figure 7, the parameter with the greatest influence on the fluctuation rule of the discrete contact point is the eccentricity, whereas variations in the other three parameters have little influence. And under the structure parameters of the numerical simulation, the maximum total friction power of the contact area between the external retainer plate and the external spherical hinge is 131 W. Changing the slant inclination of the external swash plate, the pump shaft rotating speed, or the spring force has little influence on the fluctuation rule of the friction power of the discrete contact point, whereas changes in the eccentricity values can mostly affect the fluctuation rule of the friction power of the discrete contact point.
Figure 8 describes the influence of the slant inclinations of the external swash plate, pump shaft rotating speeds, eccentricities and spring forces on the total friction power of the contact area between the external retainer plate and the external spherical hinge. As shown in Figure 8, the total friction power of the contact area varies linearly with the slant inclination of the external swash plate, pump shaft rotating speed and spring force (increasing when these parameters are increased). The total friction power of the contact area has a non-linear relationship with the eccentricity; it decreases when the eccentricity is increased and finally tends to a certain value.
Figure 9 shows the influence of the spring force on the total friction power under different structural parameters. As shown in Figure 9, the total friction power of the contact area between the external retainer plate and the external spherical hinge varies linearly with the spring force, increasing when this parameter is increased. Changes in the different structural parameters do not affect the linear relationship between the spring force and the total friction power of the contact area.
 |
Fig. 7 Comparison of the amplitude changes of the friction power for various parameters. |
 |
Fig. 8 Influence of the structural parameters on the total friction power of the contact point. |
 |
Fig. 9 Influence of the spring force on the total friction power for different structural parameters. |
6 Discussion
To ensure the reliability of the calculation, different amounts of discrete contact points were chosen to calculate the total friction power, and then, the influence of the amount of the discrete contact point on the total friction power was analysed. Figures 3a, 4a, 5a and 6a show that during one cycle (external retainer plate rotating for one circle), a discrete contact point is taken every 0.5 degrees. Figures 3b, 4b, 5b and 6b show that during one cycle (external retainer plate rotating for one circle), a discrete contact point is taken every 0.005 degrees. By comparing Figures 3a and 3b, 4a and 4b, 5a and 5b, and 6a and 6b, we can see that the amount of the discrete contact point has increased 100 times, the influences of the slant inclination of the external swash plate, pump shaft rotating speed, eccentricity and spring force on the friction-power fluctuation of the discrete contact point between the external retainer plate and the external spherical hinge remain almost unchanged, and the size of the friction power of the discrete contact point is almost 1/100 of the original. By comparing Tables 2–9, we find that the amount of discrete contact points has increased 100 times, the position of the pump shaft rotation angle corresponding to the amplitude of discrete contact points is almost invariable, and the total friction power of the discrete contact point between the external retainer plate and the external spherical hinge stays almost the same. So, if the amount of discrete contact points reaches a certain value, there is no effect on the result. The reliability of calculating the total friction power between ball hinge pairs by discretization method is also verified by experiments in reference [16].
The above analysis suggests that the friction power at each contact point and total friction power increase linearly with the slant inclination of the external swash plate, pump shaft rotating speed and spring force, and presents phenomenon of double-peak-value. There is a high friction power at pump shaft rotation angles of 90° and 270° (corresponding to the position of the centre of port plate waist groove). Due to the contact form of external return spherical bearing pair is line contact. The contact stress is large, so it is hard to form a lubricating oil film. While running at high speed, it is easy to produce friction heat and damage the surface of the friction pair.
The influence of eccentricity on the friction power of the contact point is complex. At small eccentricity values (about 5 mm) a multiple-peak value appears in the same cycle, that is, a situation of multi-point supporting occurs. However, at pump shaft rotation angles close to 90° and 270° (corresponding to the position of the centre of port plate waist groove), the maximum peak value is obviously the largest, which makes it is easy to damage the surface of the friction pair, and there exist bigger total friction power. At larger eccentricity values (about 15 mm) a double-peak value phenomenon appears, but the variation range of maximum peak value of friction power at contact point decrease obviously, and the total friction power finally tends to a certain value.
7 Conclusions
Herein, we analysed the force conditions of the external return spherical bearing pair of balanced double-row axial piston pumps and dual-drive axial piston motors, deduced the formulas of friction power of the discrete contact point and the total friction power in the external return spherical bearing pair, and discussed the influence of different structural parameters on the friction power of external retainer mechanism. The following conclusions were drawn:
The friction power of the contact area in the external return spherical bearing pair is affected by structural parameters such as slant inclination of the external swash plate, pump shaft rotating speed, eccentricity and spring force. The power fluctuation amplitude and the total friction power of the discrete contact point in the external return spherical bearing pair increase with the slant inclination of the external swash plate, pump shaft rotating speed and spring force but decrease with increasing eccentricity.
For different slant inclinations of the external swash plate and eccentricities, the power peak of a discrete contact point is located at different pump shaft rotation angle positions. At different pump shaft rotating speeds and spring forces, the power peak of a discrete contact point is located at the same pump shaft rotation angle positions. The distribution shape of the friction power of the discrete contact point was only affected by the eccentricity. At large eccentricity values, the friction power of the discrete point presents a double-peak distribution, whereas at small eccentricity values, it shows a multiple-peak distribution.
For different slant inclinations of the external swash plate, pump shaft rotating speeds, eccentricities and spring forces, the fluctuation curve of friction power of the discrete contact point in the external return spherical bearing pair is symmetrical at 180°, in the same cycle. At pump shaft rotation angles of 0° and 180°, the friction power is 0. That is an intrinsic property of the external return mechanism.
With increasing number of discrete contact points in the contact area of the external return spherical bearing pair, different structural parameters have little influence on the friction-power fluctuations at the discrete contact point; the area of friction wear and the laws of the friction-power fluctuation curve of the discrete contact point do not changed. The friction power of a single discrete contact point decreases, but the total friction power remains almost unchanged.
The total friction power of the contact area varies linearly with the slant inclination of the external swash plate, pump shaft rotating speed and spring force, increasing when these parameters increase. The total friction power of the contact area has a non-linear relation with the eccentricity, decreasing when this parameter increases until it reaches a certain value. Changes in the different structural parameters do not affect the linear relationship between the spring force and the total friction power of the contact area.
Nomenclature
fs : Coefficient of sliding friction between the external retainer plate and the external spherical hinge
Fft : Sliding friction force of an arbitrary contact point mt [N]
Nt : Normal force of an arbitrary contact point mt in the external return spherical bearing pair [N]
nt : Unit vector of the normal force at arbitrary contact point mt [N]
r : Radius of external spherical hinge [mm]
r1 : Radius of external retainer plate [mm]
ut : Unit vector of the sliding friction force at arbitrary contact point mt [N]
|ΔVt|: Magnitude of the relative motion velocity vector at arbitrary contact point mt [m/s]
α : Principal axis rotation angle [°]
β : External swash plate inclination [°]
ρ5t : Radius vector at arbitrary contact point mt [mm]
Acknowledgements
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: This paper was supported by the National Natural Science Foundation of China (Grant No. 51575002), the Top-notch Talent Program of University (Profession) in Anhui Province (gxbjZD11) and the Open Foundation of the State Key Laboratory of Fluid Power and Mechatronic Systems (GZKF-201715).
References
- H.Y. Yang, B. Zhang, B. Xu, Development of axial piston pump/motor technology, J. Mech. Eng. 44, 1–8 (2008) [Google Scholar]
- Z.Y. Quan, L. Quan, J.M. Zhang, Review of energy efficient direct pump controlled cylinder electro-hydraulic technology, Renew. Sust. Energy Rev. 35, 336–346 (2014) [CrossRef] [Google Scholar]
- V.H. Vu, B. Bechir, T. Marc, J. Pierre, Operational modal analysis on a pump operating at varying speeds an industrial history case, Mech. Ind. 17, 1–10 (2016) [Google Scholar]
- J. Mele, A. Guzzomi, J. Pan, Correlation of centrifugal pump vibration to unsteady flow under variable motor speed, Mech. Ind. 15, 525–534 (2014) [CrossRef] [Google Scholar]
- Y. Zhao, J.J. Zhou, C.B. Jing, C. Wei, Effect of grooved face on the dynamic pressure support characteristics of cylinder/valve plate pair in the axial piston pump, J. Harbin Inst. Technol. 50, 169–174 (2018) [Google Scholar]
- J.H. Zhang, Q. Chao, B. Xu, Analysis of the cylinder block tilting inertia moment and its effect on the performance of high-speed electro-hydrostatic actuator pumps of aircraft, Chin. J. Aeronaut. 31, 169–177 (2018) [CrossRef] [Google Scholar]
- H.S. Tang, Y. Ren, J.W. Xiang, A novel model for predicting thermoelastohydrodynamic lubrication characteristics of slipper pair in axial piston pump, Int. J. Mech. Sci. 124, 109–121 (2017) [CrossRef] [Google Scholar]
- M. Rokala, O. Calonius, K.T. Koskinen, M. Pietola, Study of lubrication conditions in slipper-swashplate contact in water hydraulic axial piston pump test rig, in Proceedings of the JFPS International Symposium on Fluid Power. Toyama, 2008, pp. 91–94 [CrossRef] [Google Scholar]
- J.H. Zhang, Q. Chao, Q.N. Wang, B. Xu, Y. Chen, Y. Li, Experimental investigations of the slipper spin in an axial piston pump, Measurement 102, 112–120 (2017) [CrossRef] [Google Scholar]
- Y. Li, H.S. Deng, X.L. Wang, Experiment on friction and wear performance of textured port plate pair, J. Aerospace Power 29, 1591–1597 (2014) [Google Scholar]
- H.-S. Jeong, H.-E. Kim, On the instantaneous and average piston friction of swash plate type hydraulic axial piston machines, KSME Int. J. 18, 1700–1711 (2004) [CrossRef] [Google Scholar]
- N. Vatheuer, H. Murrenhoff, U. Bräckelmann, D. Breuer, Mechanical losses in the piston-bushing contact of axial piston units, JFPS Int. J. Fluid Power Syst. 8, 24–29 (2014) [CrossRef] [Google Scholar]
- S. Lin, J.B. Hu, Tribo-dynamic model of slipper bearings, Appl. Math. Model. 39, 548–558 (2015) [Google Scholar]
- N.D. Manring, The relative motion between the ball guide and slipper retainer within an axial-piston swash-plate type hydrostatic pump, J. Dyn. Syst. Measur. Control. 121, 518–523 (1999) [CrossRef] [Google Scholar]
- Y. Sun, J.H. Jiang, J.L. Liu, Relative position and friction power loss between slipper retainer and ball guide in axial piston pump, J. South China Univ. Technol. 39, 82–87 (2011) [Google Scholar]
- Y. Sun, Y. Li, J.H. Jiang, Stress analysis and experiments for slipper retainer and ball guide in axial piston pump, J. Xi'an Jiaotong Univ. 47, 103–108 (2013) [Google Scholar]
- B. Xu, C.G. Li, S.S. Xu, Research on the relative motion between the ball guider and retainer within axial piston pump based on virtual prototype, Mach. Tool Hydraulics 38, 18–21 (2010) [Google Scholar]
- B. Zhang, B. Xu, C.L. Xia, H.Y. Yang, Modeling and simulation on axial piston pump based on virtual prototype technology, J. Mech. Eng. 22, 84–90 (2009) [Google Scholar]
- T. Wang, M. Mao, S.S. Tang, J.T. Gai, H. Ji, Research on lubrication mechanism of retaining spherical pair of variable displacement axial piston pump, Acta Armamentarii 38, 424–432 (2017) [Google Scholar]
- H.S. Deng, C.L. Wang, L.X. Zhang, Study on flow ripple of balanced two-ring axial piston pump, Trans. Chin. Soc. Agric. Mach. 45, 305–309 (2014) [Google Scholar]
- H.S. Deng, K. Huang, C.L. Wang, Y.M. Li, Overturning moment of cylinder of balanced two-ring axial piston pump, J. Jilin Univ. (Eng. Technol. Ed.) 45, 1468–1473 (2015) [Google Scholar]
- H.S. Deng, R. Huang, C.L. Wang, K. Huang, T. He, L. Zheng, A swash-plate axial piston pump/motor compacting device. Patent No.CN104863812A, China, 26 Aug 2015 [Google Scholar]
- H.S. Deng, Q.C. Wang, H.F. Wang, C.L. Wang, Relative motion relation in the external return spherical bearing pair of a balanced double-row axial piston pump, Proc. Inst. Mech. Eng. C 233, 3858–3872 (2019) [CrossRef] [Google Scholar]
Cite this article as: H. Deng, C. Hu, Q. Wang, L. Wang, C. Wang, Friction and wear analysis of the external return spherical bearing pair of axial piston pump/motor, Mechanics & Industry 21, 104 (2020)
All Tables
Friction power peak-to-valley value of a contact point under different external swash plate inclinations (m = 721).
Friction power peak-to-valley value of a contact point under different external swash plate inclinations (m = 72 001).
Contact point friction power peak-to-valley value at different pump shaft rotating speeds (m = 721).
Contact point friction power peak-to-valley value at different pump shaft rotating speeds (m = 72 001).
Contact point frictional power peak-to-valley value at different eccentricities (m = 721).
Contact point frictional power peak-to-valley value at different eccentricities (m = 72 001).
Contact point friction power peak-to-valley value under different spring force (m = 721).
Contact point friction power peak-to-valley value under different spring force (m = 72 001).
All Figures
 |
Fig. 1 Structure of the balanced double-row axial piston pump. 1. Slipper; 2. Internal swash plate; 3. Internal spherical hinge; 4. Pump shaft; 5. Front end cover; 6. External swash plate; 7. External spherical hinge; 8. Shell; 9. External retainer plate; 10. Juncture. 11. Spring seat; 12. Compression spring; 13. Plunger; 14. Valve plate; 15. Rear end cover. |
| In the text | |
 |
Fig. 2 External spherical hinge force analysis. |
| In the text | |
 |
Fig. 3 Influence of external swash plate inclinations on the friction power of the contact point. |
| In the text | |
 |
Fig. 4 Influence of the pump shaft rotating speeds on the friction power of the contact point. |
| In the text | |
 |
Fig. 5 Influence of eccentricity on the friction power of the contact point. |
| In the text | |
 |
Fig. 6 Influence of the spring forces on the friction power of the contact point. |
| In the text | |
 |
Fig. 7 Comparison of the amplitude changes of the friction power for various parameters. |
| In the text | |
 |
Fig. 8 Influence of the structural parameters on the total friction power of the contact point. |
| In the text | |
 |
Fig. 9 Influence of the spring force on the total friction power for different structural parameters. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


