| Issue |
Mechanics & Industry
Volume 22, 2021
|
|
|---|---|---|
| Article Number | 18 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.1051/meca/2021015 | |
| Published online | 17 March 2021 | |
Regular Article
Investigation of process parameters and plate local thickening on residual stresses in hot stamping process
1
School of Mechanical and Electrical Engineering, Xinyu University, Xinyu 338004, PR China
2
State Key Laboratory of Materials Processing and Die & Mould Technology, Huazhong University of Science and Technology, 1037 Luoyu Road, Wuhan 430074, PR China
3
Xinyu Engineering Technology Research Center of 3D printing manufacturing and Application, Xinyu 338004, PR China
4
School of Materials Science and Engineering, Hubei University of Automotive Technology, Shiyan 442002, PR China
* e-mail: lijinboxyxy@126.com
Received:
6
January
2021
Accepted:
12
February
2020
In this paper, local-thickened plates are adopted for aluminum alloy square cups stamping with relatively low values of residual stresses and small radius at the bottom corner. By utilizing numerical and experimental methods, the effects of process parameters and plate local thickening on the residual stress distribution of hot stamped aluminum alloy square cups are studied. Furthermore, the influence of plate local thickening on the radius of bottom corner of square cups is also investigated. The results showed that with an increase in the forming temperature, blank holder force and die corner radius, residual stresses in hot stamped square cups can be reduced. The same effect can be achieved by decreasing the die entrance radius. As opposed to the flat plates, using local-thickened plates can not only reduce the residual stresses values in hot stamped square cups, but also decrease the radius at the bottom corner of square cups. When the optimized thickening scheme of plate is used, the smaller radius at the bottom corner, the lower residual stresses in the square cups are obtained.
Key words: Residual stress / hot stamping / process parameters / plate local thickening
© J. Li et al., Published by EDP Sciences 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Owing to their beneficial properties associated with relatively low density and high specific strength, the utilization of aluminum alloy sheets for stamping manufacturing has shown an increased in recent years [1,2]. Since formability of aluminum alloy sheets is not high enough to accurately stamp parts with complex geometries at room temperature, aluminum alloy sheets stamping is conducted under increased temperatures [3,4], which is commonly known as hot stamping. However, the hot stamping of aluminum alloy sheets often results in high residual stresses in the hot stamped components according to the literature [5].
The residual stresses can significantly influence mechanical properties and dimensional stability of aluminum alloy sheet components. When these components are used in aerospace engineering, residual stresses have shown to reduce the fatigue strength. This effect, coupled with the increase risk of ionic oxygen-induced corrosion cracking, may result in early fatigue failure and consequently reduced service life of the components. Moreover, residual stress is prone to slack and redistribution due to the variable temperature of both high and low temperature in cosmic space, which can negatively impact the dimensional stability of the components. In addition, the release of residual stresses in machining process can cause a larger distortion of components and cause subsequent assembly difficulties [6,7]. Therefore, there is an urgent need to decrease residual stresses values in hot stamped aluminum alloy components.
Danckert [8] have investigated the effect of die profile on the residual stresses in a deep drawn cup. The author found that a large reduction of tangential residual stresses values in the deep drawn cup can be achieved by using a tractrix shaped die profile. Ragab and Orban [9] showed that ironing occur simultaneously with deep drawing can reduce residual stresses values in deep drawn cups at least 80%. Greze et al. [10] studied the influence of temperature on residual stresses during the deep drawing of 5754 aluminum alloys. The authors varied the forming temperature values from standard room temperature of 20–200 °C. Their results showed that it is possible to decrease residual stresses with an increase in the forming temperature. Masoud et al. [11] investigated the influence of initial blank thickness, punch radius and friction coefficients et al. on residual stresses in deep drawn cups with finite element (FE) and experimental investigations. The authors found that the minimum residual stress value in the cup wall, specifically equaling to 26 MPa, can be obtained when theses process parameters were optimized. Kleiner et al. [12,13] studied the effect of fluid pressure on residual stresses during high-pressure sheet metal forming. The authors found that the residual stresses values in sheet metal components can be reduced by increasing the fluid pressure. Wang et al. [14] studied the effect of forming temperature and relative bending radii on the residual stresses of stamping-forged V-shaped parts. Their results showed that an increase in the forming temperature and relative bending radius led to lower residual stress values. Xia et al. [15] studied the residual stresses in non-isothermal dies bending process of 2024 aluminum alloys. The results indicate that the residual stress values of blanks with room temperature can be comparable to those of the high temperature isothermal bending by proper temperature control of the punch and the die. Li et al. [5] demonstrated that by using local-thickened plates, a significant reduction of residual stress values in hot stamped square cups can be achieved.
Square cups are commonly used as support structural components in aerospace satellites, which are often designed with small radius at the bottom corner. In order to ensure the reliability of the square cups for aerospace application, low values of residual stresses are required. The material flow during the process of square cups stamping is quite inhomogeneous, making it easy to induce residual stresses. Moreover, due to technological limitations of stamping forming processes, it is also difficult to meet the requirements of low radius values at the bottom corner of square cups. Hence, a large amount of subsequent milling of the square cups is required. According to Li et al. [16], milling tends to often result in larger component deformations due to the release and redistribution of the induced residual stresses.
In order to reduce the required milling amount, local-thickened plates are adopted in this study for stamping of the aluminum alloy square cups, which have small radius at the bottom corner and consequently low values of residual stresses. FE analysis is performed to investigate the effect of forming temperature, blank holder force, die entrance radius, die corner radius and plate local thickening on the residual stress values and their distribution in square cups induced during hot stamping. Furthermore, the effect of plate local thickening on the radius of bottom corner of square cups is discussed. In order to validate the numerical results, experimental investigations of hot stamping processes are carried out whilst measuring values and observing distributions of the residual stresses. Lastly, optimized process parameters and plate thickening schemes are obtained, which could be utilized for production of the square cups with low values of residual stresses and small radius at the bottom corner.
2 Finite element simulation
Numerical analysis is conducted to investigate the effects of process parameters and plate local thickening on the residual stress values of hot stamped square cups. Four local-thickened plates and a single flat plate used for square cup hot stamping in this study are presented in Figure 1 [5]. The shape and the size of the local-thickened plates as well as the flat plate are shown in Figure 1.
Owing to double-symmetric boundary conditions, only a quarter of the three-dimensional FE model of hot stamping of square cups can be modelled. The model is developed via ABAQUS/Explicit computer software as elastic-plastic, coupled with thermo-mechanical 2024 aluminum alloy local-thickened plates, as shown in Figure 2 [5]. The tools are considered as ideally rigid but non-isothermal.
For 2024 aluminum alloy, the Poisson's ratio is taken as 0.31, Young modulus is in the range of 72–40 GPa. Furthermore, the specific heat, thermal expansion coefficient and thermal conductivity is set as 924 J/(kg·K), 6.6e-5/K, and 190 W/(m·K) respectively. In addition, heat transfer coefficient between plate and tools as well as that between plate and the environment is 2000 W/(m2·K) and 40 W/(m2·K), respectively. The plate is defined as elastic-plastic body. The interior of plate is considered as homogeneous and isotropic. In addition, the material of plate follows the von Mises yield criterion. The stress versus strain relations of 2024 aluminum alloy at various temperatures are presented in Figure 3 [5].
Friction and contact heat boundary conditions are modelled at the interfaces between the tools and the plate. During the numerical analysis, the coulomb friction model is employed. At the same time, the friction coefficients are assumed to be constant for the duration of the analysis. The hot stamping parameters of square cup are listed in Table 1 [5]. The non-isothermal calculations of hot stamping are carried out via explicitly coupled temperature-displacement formulation. Following the removal of the tools and the cooling process of the hot stamped square cup to room temperature (taken as 25 °C), the residual stresses values in square cup are extracted.
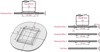 |
Fig. 1 Shape and size of the local-thickened plates and flat plate used in square cup hot stamping. |
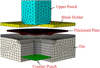 |
Fig. 2 The three-dimensional FE model of hot stamping of square cups. |
 |
Fig. 3 Stress versus strain relations of 2024 aluminum alloy (strain rate is 0.1/s). |
3 Experimental setup
3.1 Hot stamping of square cups
Figure 4 shows the schematic representation of square cup hot stamping [5]. For hot stamping process of square cups with local-thickened plates, upper punch radius, blank holder force and forming temperature are 10 mm, 32 kN and 400 °C respectively. Die entrance radius as well as die corner radius is 15 mm. For experimental investigations with the flat plates, the upper punch radius, die entrance radius as well as die corner radius are keep consistent with that used in the local-thickened plates. The forming temperatures are 300 and 450 °C, and the blank holder forces are 24 and 40 kN respectively.
Commercially acquired 2024 aluminum alloy plate is used as the raw materials in this study. The plate is machined to local-thickened plates and flat plates according to the schemes in Figure 1. Hot stamping experiments are carried out on a deep drawing hydraulic press. The maximum tonnage of the hydraulic press is 500 tons. Prior to the hot stamping experiments, the counter punch, die as well as blank holder are heated to 150 °C, while the upper punch is not heated. At the start of the experiment, water-based graphite is sprayed on the surfaces of upper punch, blank holder, die, and counter punch for lubrication. The plate is heated in a box-resistor-stove. The plate is quickly placed on the pre-heated die and immediately stamped after it reaches the predetermined forming temperature. The speed of upper punch is 10 mm/s and the drawing height of square cup is 60 mm. When using the Thickened plate 2, the manufactured hot stamped square cup is shown in Figure 5.
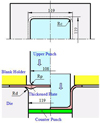 |
Fig. 4 Schematic representation of hot stamping of square cup with local-thickened plate. |
 |
Fig. 5 A manufactured hot stamped square cup by employing the Thickened plate 2. |
3.2 Residual stress measurement
Before analyzing the simulation results of residual stresses, three characteristic points are selected at the bottom, the wall and the die entrance radius of the square cup along the symmetrical curve AD. These three points are designed as points A, B, and C respectively. This is presented in Figure 6. Distribution of the tangential residual stress along the plate thickness direction at points A, B, and C is analyzed in detail. As shown in Figure 6, the direction indicated by the arrow defined as the tangential direction. For the numerical simulations, after the hot stamping process is completed, the tools are first removed, and then the hot stamped square cup is cooled to room temperature (taken as 25 °C). Then, the tangential stress values at nodes along the thickness direction of the cup at points A, B, and C are extracted.
In order to validate the numerical simulations, tangential residual stress along the thickness direction of cup at points B is actually measured. Electro-polishing is applied to remove the thin layers of the material with great precision. The adhesive tape is utilized for square cup protection to ensure that only the area designed for polishing is in contact with the electrolyte. The electro-polishing is carried out using saturated ammonium chloride solution and the optimum voltage, with current parameters set at 20 V and 1 A. Thickness of the removed layer in each increment of electro-polishing is 0.2 mm. Following the layer removal, the X-ray diffraction method is applied to determine the residual stress magnitudes at points of interest. All the measurements are concluded with an X-350A X-ray residual stress measuring instrument. The parameters of residual stress measurement are consistent with that set in the literature [5].
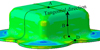 |
Fig. 6 Locations of the points A, B and C and arrow direction. |
4 Results and discussion
4.1 Influence of forming temperature on residual stresses
Investigations on the influence of forming temperature on the residual stress values and distribution in hot stamped square cups are carried out by employing the forming temperature of 300, 350, 400 and 450 °C. Meanwhile, the die entrance radius and die corner radius are both equal to 15 mm, while the blank holder force is kept at 32 kN. The tangential residual stress distribution in the cup bottom, cup wall and die entrance radius of square cups at various forming temperatures are shown in Figure 7. Difference between the residual stress distributions can be observed. The tangential residual stresses along the thickness direction of the cup bottom are tensile in the external layer, while compressive in the internal layer (Fig. 7a). The tangential residual stress along the thickness direction of the cup wall varies as compressive-tensile-compressive from the external surface to the internal surface (Fig. 7b). The tangential residual stress along the thickness direction of the die entrance radius presents a tensile-compressive-tensile variation from the external surface to the internal surface (Fig. 7c).
With an increase in the forming temperatures, lower residual stresses in the hot stamped square cups can be observed. As shown in Figure 7a, tangential residual stresses in the cup bottom can be reduced from +92 to −136 MPa to +58 to −70 MPa, when increasing the forming temperature from 300 to 450 °C. For tangential residual stresses in the cup wall, residual stress values can be reduced from +170 to −208 MPa to +120 to −133 MPa (Fig. 7b). Lastly, tangential residual stresses in the die entrance radius of square cups can be reduced from +92 to −117 MPa to +21 to −76 MPa (Fig. 7c). It is a well-known fact that as the forming temperature increases, the yield stress values of metal materials gradually decreases. Moreover, the value of yield stress of metal materials during forming is the limiting value of residual stresses. Hence, it can be concluded that the residual stresses can be effectively reduced by increasing the forming temperatures [5]. In Figure 7d, comparison of the tangential residual stresses in the cup wall obtained from both numerical simulations and experimental measurements carried out at 300 and 450 °C is presented. It can be observed that numerical simulation results show good agreements with the experimental measurement data.
 |
Fig. 7 Tangential residual stress distribution in the (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups at various forming temperatures, and (d) comparison of the residual stresses in the cup wall obtained from numerical simulations and experimental measurements. |
4.2 Influence of blank holder force on residual stresses
The influence of blank holder force on the residual stress values and distribution in hot stamped square cups are investigated by employing the blank holder force of 24, 28, 32, 36 and 40 kN. Meanwhile, forming temperature, die corner radius and die entrance radius are kept constant at 400 °C, 15 and 15 mm respectively. The tangential residual stress distribution in the cup bottom, cup wall and die entrance radius of square cups under various blank holder forces are shown in Figure 8.
From Figure 8, it can be observed that a larger blank holder force reduce the values of residual stresses in the cup bottom as well as die entrance radius of square cup. Nevertheless, the residual stresses in the cup wall are increasing slowly with an increase in the blank holder force. This indicates that the residual stresses in the cup wall are mostly unaffected by blank holder forces. As shown in Figure 8a, tangential residual stresses in the cup bottom can be reduced from +87 to −101 MPa to +63 to −78 MPa, when increasing the blank holder force from 24 to 40 kN. For tangential residual stresses in the cup wall, residual stresses values can be reduced from +172 to −196 MPa to +152MPa to −182 MPa (Fig. 8b). Lastly, tangential residual stresses in the die entrance radius of square cups can be reduced from +80 to −103 MPa to +55MPa to −73 MPa (Fig. 8c). Fig. 8d displays the comparison of the tangential residual stresses in the cup wall between the values obtained from numerical simulations and experimental measurements, with the blank holder force is 24 and 40 kN respectively. Numerical simulation results have shown good correlation with the experimental data. The residual stresses are induced as a result of inhomogeneous localized plastic deformations during the process of hot stamping. With an increase in strain inhomogeneous degree, induced residual stresses are also enlarged. Figure 9 shows the simulation results of true strain gradients between the external and the internal surface at the cup wall under various blank holder forces. It can be observed that a larger blank holder forces reduce the true strain gradients between the external and the internal surfaces of the cup wall. This indicates that by increasing the blank holder force, strain inhomogeneous degree along the thickness of the cup wall is lowered, which in turn results in a decrease of residual stresses. In a similar manner, by comparing the true strain gradients between the external and the internal surface at the bottom and die entrance radius of square cups, it can be noticed that with an increase of the blank holder forces values, a decrease in true strain gradients at the bottom and the die entrance radius is observed, which results in lower residual stresses.
 |
Fig. 8 Tangential residual stress distribution in the (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups under various blank holder forces, and (d) comparison of the residual stresses in the cup wall obtained from numerical simulations and experimental measurements. |
 |
Fig. 9 True strain gradients between the external and the internal surface at the cup wall of square cups under various blank holder forces. |
4.3 Influence of die entrance radius on residual stresses
Investigations on the influence of die entrance radius on the residual stress values and distribution are carried out, where values of 13, 15, 17 and 20 mm are chosen for die entrance radii. Meanwhile, forming temperature, blank holder force and die corner radius are kept constant at 400 °C, 32 kN and 15 mm respectively. The tangential residual stress distributions in the cup bottom, cup wall and die entrance radius of the square cups under various die entrance radii are shown in Figure 10.
From Figure 10, it can be observed that a smaller die entrance radius reduces the residual stresses in the cup bottom, the cup wall and the die entrance radius of hot stamped square cups. As shown in Figure 10a, tangential residual stresses in the cup bottom can be reduced from +95 MPa to −110 MPa to +55 to −60 MPa, when decreasing the die entrance radius from 20 to 13 mm. For tangential residual stresses in the cup wall, residual stresses values can be reduced from +170 to −212 MPa to +148 ∼ −190 MPa (Fig. 10b). Lastly, tangential residual stresses in the die entrance radius of square cups can be reduced from +74 to −110 MPa to +57 to −80 MPa (Fig. 10c). Figure 11 shows the true strain gradients between the external and the internal surface at the cup wall under various die entrance radii. It can be observed that a smaller die entrance radius reduce the true strain gradients. This indicates that by decreasing the die entrance radius, strain inhomogeneous degree along the thickness of the cup wall is lowered, which in turn results in a decrease of residual stresses. Similarly, by comparing the true strain gradients between the external and the internal surface at the bottom and die entrance radius of square cups respectively under various die entrance radii, it can be noticed that with an decrease of the die entrance radius values, a decrease in true strain gradients at the bottom and the die entrance radius is observed, which results in lower residual stresses.
 |
Fig. 10 Tangential residual stress distribution in the (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups under various die entrance radii. |
 |
Fig. 11 True strain gradients between the external and the internal surface at the cup wall of square cups under various die entrance radii. |
4.4 Influence of die corner radius on residual stresses
The influence of die corner radius on the residual stress values and distribution are carried out, where values of 10, 13, 15, 17 and 20 mm are chosen for dies corner radii. Meanwhile, forming temperature, blank holder force and die entrance radius are kept constant at 400 °C, 32 kN and 15 mm respectively. The tangential residual stress distribution in the cup bottom, cup wall and die entrance radius of square cups at various die corner radii are presented in Figure 12.
From the obtained simulation results, it can be observed that a larger die corner radius reduces residual stresses in the cup bottom. However, the residual stresses in the cup wall and die entrance radius of the square cups are found to decrease relatively slowly with an increase in the die corner radius. Hence, it can be concluded that the residual stresses in the cup wall, as well as die corner radius of the square cups, are not sensitive to die corner radius. As shown in Figure 12a, tangential residual stresses in the cup bottom can be reduced from +86 MPa to −125 to +52 MPa to −63 MPa, when increasing the die corner radius from 10 to 20 mm. For tangential residual stresses in the cup wall, residual stresses values can be reduced from +158 to −194 MPa to +141 to −180 MPa (Fig. 12b). Lastly, tangential residual stresses in the die entrance radius of square cups can be reduced from +80 to −96 MPa to +62 to −81 MPa (Fig. 12c). Figure 13 shows the true strain gradients between the external and the internal surface at the cup wall under various die corner radii. It can be observed that a larger die corner radius reduce the true strain gradients. This indicates that by increasing the die corner radius, strain inhomogeneous degree along the thickness of the cup wall is lowered, which in turn results in a decrease of residual stresses. Similarly, by comparing the true strain gradients between the external and the internal surface at the bottom and die entrance radius of square cups, it can be noticed that with an increase of the die corner radius values, a decrease in true strain gradients at the bottom and the die entrance radius is observed, which results in lower residual stresses.
 |
Fig. 12 Tangential residual stress distribution in the (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups under various die corner radii. |
 |
Fig. 13 True strain gradients between the external and the internal surface at the cup wall of square cups under various die corner radii. |
4.5 Influence of plate local thickening on residual stresses
The distributions of tangential residual stress in the cup bottom, cup wall and die entrance radius of square cups, which are obtained from local-thickened plates, are compared with those obtained from flat plates, as shown in Figure 14. It can be seen that the residual stress values in square cups are reduced significantly when using local-thickened plates instead of flat plates. To further investigate the effect of plate local thickening, the residual stresses in square cups, which were obtained from the Thickened plate 2, are compared with those obtained from flat plates at 400 °C. As shown in Figure 14a, tangential residual stress in the cup bottom can be reduced from +69 to −90 MPa to +30 to −32.5 MPa, when using the Thickened plate 2 instead of the flat plat. For tangential residual stresses in the cup wall, residual stress values can be reduced from +158 to −190 MPa to +125 to −32 MPa (Fig. 14b). Lastly, tangential residual stresses in the die entrance radius of square cups can be reduced from +69 to −96 MPa to +43 to −9 MPa (Fig. 14c). Especially in the external layer of the die entrance radius, the tangential stress values can be reduced to approximately zero when Thickened plate 2 is utilized. Figure 14d displays the comparison of the tangential residual stresses in the cup wall of Thickened plate 2, which are obtained from numerical simulations and experimental measurement. It is demonstrated that the finite element simulation results show good agreements with the experimental results.
As displayed in Figure 14, the residual stress distributions in the hot stamped square cups made from Thickened plate 1, 2, 3 and 4 are very similar. But by carefully comparing these residual stress values, it can be realized that ranges of the tangential residual stresses in all three characteristic locations are smallest when using Thickened plate 2. For example, when Thickened plate 1, 3 and 4 are employed, the ranges of tangential residual stress values in the cup wall are +194 to −82 MPa, +137 to −64 MPa and +178 to −50 MPa. This range can be reduced to +125 to −32 MPa when Thickened plate 2 is used. As presented in Figure 15, when using Thickened plate 2, true strain gradient between the external and the internal surface of the cup wall is smallest. This indicates that by employing Thickened plate 2, smaller strain inhomogeneous degree along the thickness of the cup wall is observed, which results in lower residual stress values. In a similar manner, a comparison can be made between the true strain gradients between the external surface and the internal surface at the cup bottom as well as the die entrance radius of square cup. The results indicate that when utilizing Thickened plate 2, lower true strain gradients are present, which consequently causes lower residual stresses.
 |
Fig. 14 The comparisons of residual stresses of thickened plates and flat plates of (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups, and (d) comparison of the residual stresses in the cup wall obtained from numerical simulations and experimental measurements. |
 |
Fig. 15 True strain gradients between the external and the internal surface at the cup wall of square cups with various thickened plates. |
4.6 Shapes of bottom corners with various thickened plates
The longitudinal section profiles of the bottom corners and thickness distributions along the symmetrical curve AD of hot stamped square cups which are obtained from various thickened plates are shown in Figures 16 and 17 respectively. It is revealed in Figure 16 that the FE simulation results show good agreements with the experimental results. Although these four kinds of local-thickened plates all achieve the small radius feature with different degrees at the bottom corner of square cups when compared with flat plates, the thickening effects of these four local-thickened plates are significantly different. Especially for the Thickened plate 1, when the convex rib faces upward, the radius of the bottom corner is significantly larger than that when the convex rib faces downward. According to the thickness distributions of square cups as shown in Figure 17, the thickness at bottom corner is the largest when using the Thickened plate 2. It is indicated that the Thickened plate 2 can compensate the bottom corner of square cups with more material and is more conducive to obtaining small radius feature at the bottom corner. In order to accurately compare the obtained small radius effects of the bottom corner of various thickened plates, we define the bottom corner height as b, width as h and area S = b × h/2 in this study. The values of b, h and S of square cups according experimental results are shown in Figures 18 and 19. It is shown in Figure 18 that the values of h and b can be significantly reduced from nearly 18 mm of flat plates to less than 10 mm when local-thickened plates are used. Compared among the values of h and b of these four thickened plates, the Thickened plate 2 obtains the minimum h of 4.4 mm and the Thickened plate 1 obtains the maximum h of 8.5 mm. The maximum b of 9.98 mm is obtained when the Thickened plate 4 is used. However, the Thickened plate 3 obtains the minimum b of 5.2 mm. It is shown in Figure 19 that the values of S can be significantly reduced when the Thickened plate 2 is used. Thus it is demonstrated that the Thickened plate 2 can obtain the best thickening effect at the bottom corner. According to above analyses, when the Thickened plate 2 is used, the smaller radius at the bottom corner of square cups can be obtained. Mori et al. [17] and Wang et al. [18] upset the cup wall after stamping to reduce the bottom corner radius of parts. However, both die structures and forming processes are more complicated in those two studies, in comparison with adopting local-thickened plates in this study.
As shown in Figure 1, when the Thickened plate 1 used for square cup hot stamping, the thickened convex rib faces upward. During the hot stamping, the convex rib facing upward can make the thickened metal material severely deformed, which causes a greater volume of thickened metal material flowing to the bottom and the cup wall of the square cup. As displayed in Figure 1, when the Thickened plate 4 used for square cup hot stamping, the side length of thickened convex rib is 114 mm. During the hot stamping, a large volume of the thickened metal material is extruded to the cup wall, leading to the thickened metal material cannot be accumulated at the bottom corner. When the Thickened plate 3 is used, the side length of the thickened convex rib is 102 mm, as shown in Figure 1. During the hot stamping, a large volume of the thickened metal material is retained at the cup bottom at the beginning. In the further hot stamping, only a small volume of thickened metal material at the bottom flows to the bottom corner, leading to the thickened metal material unaccumulated at the bottom corner. As displayed in Figure 1, when the Thickened plate 2 is used, the side length of the thickened convex rib equal to the upper punch width 108 mm. At the beginning stage of hot stamping, the thickened metal material is accurately supplemented at the bottom corner. In the further hot stamping, the thickened metal material is slightly extruded, and a smaller volume of thickened metal material flows to the bottom and the cup wall. Therefore, a smaller radius at the bottom corner of square cup can be obtained by using the Thickened plate 2.
In conclusion, when the Thickened plate 2 is used (i.e. the optimized thickening scheme of plate is used), the smaller radius at the bottom corner, the lower residual stresses in the square cups can be obtained.
 |
Fig. 16 The longitudinal section profiles of the bottom corners along the curve AD of hot stamped square cups with various thickened plates. |
 |
Fig. 17 Thickness distributions of hot stamped square cups with various thickened plates. |
 |
Fig. 18 The values of h and b with various thickened plates. |
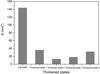 |
Fig. 19 The values of S with various thickened plates. |
5 Conclusions
In this study, local-thickened plates were adopted to stamp 2024 aluminum alloy square cups with low values of residual stresses and small radius at the bottom corner. The following conclusions are made:
-
The residual stress distributions in the cup bottom, cup wall and die entrance radius of hot stamped square cups are different when compared to each other. The tangential residual stress in the cup bottom is tensile in the external layer, while remaining compressive in the internal layer. The tangential residual stress in the cup wall varies as compressive-tensile-compressive from the external surface to the internal surface. Lastly, the tangential residual stress in the die entrance radius of square cup presents a tensile-compressive-tensile variation from the external surface to the internal surface.
-
According to the presented results, residual stresses in hot stamped square cups can be decreased in one of two ways: by either increasing the forming temperature, blank holder force and die corner radius, or by decreasing the die entrance radius.
-
In the cup wall, the tangential residual stress exhibits a little change with an increase in blank holder forces and die corner radii. In the die entrance radius of square cup, the tangential residual stress exhibits a little change with an increase in die corner radii.
-
As opposed to flat plates, using local-thickened plates can not only reduce the residual stresses values in hot stamped square cups, but also decrease the radius at the bottom corner of square cups. When the optimized thickening scheme of plate is used, the square cup with smaller radius at the bottom corner and lower residual stresses can be obtained.
Conflicts of Interest
The authors declare no conflict of interest.
Acknowledgments
The Project was Supported by State Key Laboratory of Materials Processing and Die & Mould Technology, Huazhong University of Science and Technology (No.: P2020-022), Science and Technology Research Project of Jiangxi Provincial Department of Education (No.: GJJ181034) and the Key Laboratory of Automotive Power Train and Electronic in Hubei University of Automotive Technology (ZDK1202005).
References
- A. Heinz, A. Haszler, C. Keidel, S. Moldenhauer, R. Benedictus, W.S. Miller, Recent development in aluminium alloys for aerospace applications, Mater. Sci. Eng. A 280, 102–107 (2000) [Google Scholar]
- J.A. Ferreira, P. Sun, J.J. Gracio, Close loop control of a hydraulic press for springback analysis, J. Mater. Process. Technol. 177, 377–381 (2006) [Google Scholar]
- P.F. Bariani, S. Bruschi, A. Ghiotti, F. Michieletto, Hot stamping of AA5083 aluminum alloy sheets, CIRP Ann-Manuf. Techn. 62, 251–254 (2013) [Google Scholar]
- G.L. Chen, M.H. Chen, N. Wang, J.W. Sun, Hot forming process with synchronous cooling for AA2024 aluminum alloy and its application, Int. J. Adv. Manuf. Technol. 86, 133–139 (2016) [Google Scholar]
- J.B. Li, L. Deng, X.Y. Wang, J.S. Jin, Research on residual stresses during hot stamping with flat and local-thickened plates, Int. J. Adv. Manuf. Technol. 92, 2987–2999 (2017) [Google Scholar]
- Z.J. Wang, W.Y. Chen, Y.D. Zhang, Z.T. Chen, Q. Liu, Study on the machining distortion of thin walled part caused by redistribution of residual stress, Chin. J. Aeronautics 18, 175–179 (2005) [Google Scholar]
- X.M. Huang, J. Sun, J.F. Li, Finite element simulation and experimental investigation on the residual stress-related monolithic component deformation, Int. J. Adv. Manuf. Technol. 77, 1035–1041 (2015) [Google Scholar]
- J. Danckert, Reduction of the residual stresses in a deep drawn cup by modifying the draw die profile, CIRP Ann. Manuf. Technol. 44, 259–262 (1995) [Google Scholar]
- M.S. Ragab, H.Z. Orban, Effect of ironing on the residual stresses in deep drawn cups, J. Mater. Process. Technol. 99, 54–61 (2000) [Google Scholar]
- R. Greze, P.Y. Manach, H. Laurent, S. Thuillier, L.F. Menezes, Influence of the temperature on residual stresses and springback effect in an aluminium alloy, Int. J. Mech. Sci. 52, 1094–1100 (2010) [Google Scholar]
- K. Masoud, P. Ali, A. Ali, Influence of process parameters on residual stresses in deep-drawing process with FEM and experimental evaluations, J. Braz. Soc. Mech. Sci. 40, 157 (2018) [Google Scholar]
- M. Kleiner, R. Krux, W. Homberg, Analysis of residual stresses in high-pressure sheet metal forming, CIRP Ann. Manuf. Technol. 53, 211–214 (2004) [Google Scholar]
- C. Bruni, M. Celeghini, M. Geiger, F. Gabrielli, A study of techniques in the evaluation of springback and residual stress in hydroforming, Int. J. Adv. Manuf. Technol. 33, 929–939 (2007) [Google Scholar]
- X.Y. Wang, L. Deng, J.B. Li, Encyclopedia of aluminum and its alloys, 1st edn., Taylor & Francis Group, Abingdon, UK, 2018 [Google Scholar]
- L.J. Xia, L. Deng, J.S. Jin, X.Y. Wang, Influence of non-isothermal dies on bending springback and residual stress for aluminum alloy 2024, Forging Stamp. Technol. 41, 92–95 (2016) [Google Scholar]
- B.Z. Li, X.H. Jiang, J.G. Yang, S.Y. Liang, Effect of depth of cut on the redistribution of residual stress and distortion during the milling of thin-walled part, J. Mater. Process. Technol. 216, 223–233 (2015) [Google Scholar]
- K. Mori, S. Nishijima, C.J. Tan, Two-stage cold stamping of magnesium alloy cups having small corner radius, Int. J. Mach. Tools Manuf. 49, 767–772 (2009) [Google Scholar]
- X.Y. Wang, W.T. Luo, J.C. Xia, G.A. Hu, Investigation of warm stamping forging process for car flywheel panel, Forging Stamp. Technol. 34, 33–36 (2009) [Google Scholar]
Cite this article as: J. Li, X. Chen, X. Liu, Investigation of process parameters and plate local thickening on residual stresses in hot stamping process, Mechanics & Industry 22, 18 (2021)
All Tables
All Figures
 |
Fig. 1 Shape and size of the local-thickened plates and flat plate used in square cup hot stamping. |
| In the text | |
 |
Fig. 2 The three-dimensional FE model of hot stamping of square cups. |
| In the text | |
 |
Fig. 3 Stress versus strain relations of 2024 aluminum alloy (strain rate is 0.1/s). |
| In the text | |
 |
Fig. 4 Schematic representation of hot stamping of square cup with local-thickened plate. |
| In the text | |
 |
Fig. 5 A manufactured hot stamped square cup by employing the Thickened plate 2. |
| In the text | |
 |
Fig. 6 Locations of the points A, B and C and arrow direction. |
| In the text | |
 |
Fig. 7 Tangential residual stress distribution in the (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups at various forming temperatures, and (d) comparison of the residual stresses in the cup wall obtained from numerical simulations and experimental measurements. |
| In the text | |
 |
Fig. 8 Tangential residual stress distribution in the (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups under various blank holder forces, and (d) comparison of the residual stresses in the cup wall obtained from numerical simulations and experimental measurements. |
| In the text | |
 |
Fig. 9 True strain gradients between the external and the internal surface at the cup wall of square cups under various blank holder forces. |
| In the text | |
 |
Fig. 10 Tangential residual stress distribution in the (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups under various die entrance radii. |
| In the text | |
 |
Fig. 11 True strain gradients between the external and the internal surface at the cup wall of square cups under various die entrance radii. |
| In the text | |
 |
Fig. 12 Tangential residual stress distribution in the (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups under various die corner radii. |
| In the text | |
 |
Fig. 13 True strain gradients between the external and the internal surface at the cup wall of square cups under various die corner radii. |
| In the text | |
 |
Fig. 14 The comparisons of residual stresses of thickened plates and flat plates of (a) cup bottom, (b) cup wall and (c) die entrance radius of square cups, and (d) comparison of the residual stresses in the cup wall obtained from numerical simulations and experimental measurements. |
| In the text | |
 |
Fig. 15 True strain gradients between the external and the internal surface at the cup wall of square cups with various thickened plates. |
| In the text | |
 |
Fig. 16 The longitudinal section profiles of the bottom corners along the curve AD of hot stamped square cups with various thickened plates. |
| In the text | |
 |
Fig. 17 Thickness distributions of hot stamped square cups with various thickened plates. |
| In the text | |
 |
Fig. 18 The values of h and b with various thickened plates. |
| In the text | |
 |
Fig. 19 The values of S with various thickened plates. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


