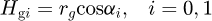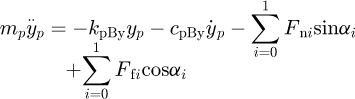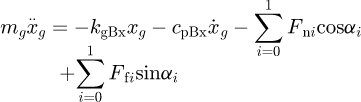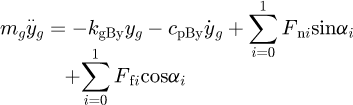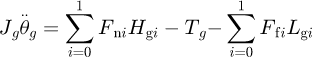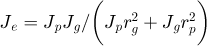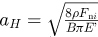| Issue |
Mechanics & Industry
Volume 23, 2022
|
|
|---|---|---|
| Article Number | 10 | |
| Number of page(s) | 12 | |
| DOI | https://doi.org/10.1051/meca/2022009 | |
| Published online | 14 June 2022 | |
Regular Article
An efficient dynamics model of spur gear drive with curved path of contact in mixed elastohydrodynamic lubrication
1
College of Mechanical and Electrical Engineering, Nanjing University of Aeronautics and Astronautics, Yudao street 29#, 210016
Nanjing, China
2
National Key Laboratory of Science and Technology on Helicopter Transmission, Nanjing University of Aeronautics and Astronautics, Yudao street 29#, 210016
Nanjing, China
* e-mail: liulei6278@nuaa.edu.cn
Received:
28
September
2021
Accepted:
23
March
2022
Design of new tooth shapes have been the focus of gear researchers aimed at overcoming the defects of involute gears. For the spur gear drive with curved path of contact, normal contact loads between engaged teeth vary in direction and magnitude, which makes it difficult to build the dynamics model of the gear drive. The current models treat the curved path of contact as an equivalent straight line without considering directional variation of normal tooth loads. This paper presents an efficient tribo-dynamics integrated model for this type of gear drive including effects of alternate meshing of single-double tooth pairs. Directional variation of normal tooth loads is considered by invoking geometric parameters of meshing points instantly. And the transient lubrication properties in mixed elastohydrodynamic lubrication are also taken into account without extensive numerical simulations. The dynamics model of a gear drive with constant relative curvature (CRC gear drive) is given as an example. The model is verified with the results of the finite element model. The results indicate that the CRC gear drive has advantages over the involute gear drive in terms of lubrication performance and mechanical efficiency. The proposed model can be used to analyze dynamics features of gear drives with curved path of contact comprehensively.
Key words: Curved path of contact / normal tooth load / dynamics model / lubrication properties
© L. Liu and J. Ni, Published by EDP Sciences 2022
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Gears are the basic components in accurate power and rotation transmission from a motor to a work machine. As far as gear drives with parallel axes are concerned, involute gear flank geometries are still the most commonly used in general applications. However, the involute gear has some defects. For example, there exists large sliding friction between tooth surfaces, inducing wear and heat easily, which affects the transmission stability, efficiency and service life. Moreover, the relative radius of curvature is small due to the convex-convex fit, which limits the contact bearing capacity. Therefore, numerous researchers and gear developers have focused on the design of non-involute gears. A variety of tooth forms have been invented and applied in different fields such as Wildhaber-Novikov gears [1], stepped triple circular-arc gears [2], logix gears [3], convoloid gearing [4], cosine gears [5], circular-arc curvilinear tooth gears [6], point-line meshing gears [7] and S-gears [8]. Besides, Wang [9] designed a new gear utilizing a parabolic curve as the line of action. Liu [10] presented a design method of tooth profiles based on control of the relative curvature at contact points. Most of above gears are spur gears like [3,5,8,9,10]. Unlike involute spur gears, paths of contact of the aforementioned non-involute gear drives are curved, which makes it difficult to establish their dynamics models. Specifically, normal loads between engaged teeth vary with contact points both in direction and magnitude. Consequently, the normal loads on simultaneous meshing tooth pairs act in different directions, and dynamic behavior of tooth pairs are also different. The classical torsional vibration model used for involute gear drives can no longer handle this issue. By far there is few literatures on dynamics model of spur gear drives with curved path of contact. Huang [11] analyzed dynamic features of the logix gear drive by use of the equivalent straight path of contact. The dynamics model neglected directional variation of normal tooth loads, unable to provide transient friction forces and normal contact forces on simultaneous meshing tooth pairs.
Moreover, more advanced models for gear dynamics have been put forward, including the effects of tooth friction in recent years. Vaishya [12] proposed a rigorous analytical treatment explicitly including the periodic nature of friction in conjunction with the time-varying mesh properties. They also provided alternative strategies for incorporating friction in the dynamic analysis of a gear drive. Song [13] developed a new method of incorporating the sliding friction and realistic time-varying stiffness into an analytical (multi-degree-of-freedom) spur gear model. And Benedict and Kelly’s friction model was used to calculate the coefficient of friction. Liu [14] studied the impacts of friction on parametric instabilities and dynamic response of a single-mesh gear drive. The friction bending effect on dynamic response was validated by finite element results. Li [15] built a non-linear time-varying dynamics model of a spur gear drive to estimate the instantaneous tooth contact force. The tooth force was fed into the elastohydrodynamic lubrication (EHL) model to simulate the transient lubrication behavior from the start of active profile to the tooth tip. Fietkau [16] developed a new efficient method of transient elastohydrodynamic gear contact simulation which incorporated oil films and elastic deformations directly into the multi-body model. In above studies except [16], oil films and tooth deformations were neglected or just implemented indirectly, i.e., the normal tooth load was given as a priori. Actually, it is a tough job to integrate the EHL equations directly with gear dynamics models. But it is feasible and effective to couple an appropriate friction model including transient lubrication properties with the accurate gear dynamics model. And such a treatment is of acceptable accuracy from an engineering point of view.
In view of tooth shape’s specialty, an efficient and accurate dynamics model for the gear drive with curved path of contact is in great request. Therefore, the main objective of this paper is to set up a vigorous multi-degree-of-freedom analytical model for a spur gear drive with curved path of contact to comprehend its dynamic characteristics. The model can account for the effects of directional variation of normal tooth loads, continuous alternate engagement and the transient lubrication properties in mixed EHL conditions.
2 Mathematical model
The number of tooth pairs meshing at the same time varies periodically in running of a gear drive. Accordingly, the mesh stiffness makes a cyclic change, and the status of tooth pairs varies with contact points. For a gear drive with curved path of contact, the normal loads of simultaneous meshing tooth pairs are different in direction and magnitude. The traditional torsional vibration models cannot take into account forces on each tooth pair separately. As described in reference [13], it is necessary to consider dynamics behavior of each meshing tooth pair in dynamics models.
Supposing the contact ratio ε∈(1,2), the contact pattern for a spur gear drive can be described in Figure 1. Point Bg is the start point of a mesh cycle, which is the intersection of tip circle of the gear and path of contact. Point Bp, the intersection of tip circle of the pinion and path of contact, represents the end point of meshing. When tooth pair #1 just comes into mesh at point Bg, the preceding tooth pair, pair #0, is contacting at point Cg, i.e. the highest point of single tooth contact (HPSTC). As the gears roll, when pair #1 engages at the lowest point of single tooth contact (LPSTC), point Cp, pair #0 leaves the mesh region just at Bp. Then pair #1 passes through the pitch point P, and the change in direction of relative sliding velocity of teeth leads to a reversal of the friction force, which brings about an impulse excitation to the system. Finally, pair #1 separates at point Cg, and one mesh cycle ends. From point Bg to Cg, the angular displacement of the pinion is φc = 2π/Zp. Accordingly, the duration for one mesh cycle is as follows
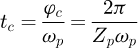 (1)
(1)
When two tooth pairs are in mesh simultaneously, the difference of angular displacement between two contact points is always equal to φc. In particular, involute gears not only satisfy this condition, but also the distance between two contact points along the path of contact is constant.
 |
Fig. 1 Contact pattern in spur gear drive with curved path of contact. |
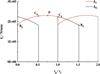 |
Fig. 2 Mesh stiffness of tooth pairs. |
2.1 Time-varying mesh stiffness
The mesh stiffness of a single tooth pair can be expressed as follows 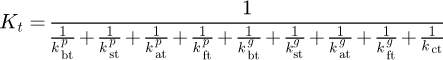 (2)
(2)
Based on theory of mechanics of materials, bending stiffness 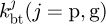 , shear stiffness
, shear stiffness 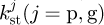 , axial compressive stiffness
, axial compressive stiffness 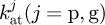 , fillet foundation stiffness
, fillet foundation stiffness 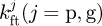 and contact stiffness [17]. kct can be calculated respectively. From the above stiffness, the mesh stiffness of an engaged tooth pair is then obtained over a mesh cycle. Considering the periodicity of the system, the mesh stiffness function of the ith tooth pair is expressed as
and contact stiffness [17]. kct can be calculated respectively. From the above stiffness, the mesh stiffness of an engaged tooth pair is then obtained over a mesh cycle. Considering the periodicity of the system, the mesh stiffness function of the ith tooth pair is expressed as 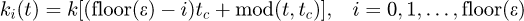 (3)
(3)
Where, the ‘‘floor’’ function rounds the value of contact ratio down to the nearest integer.
If ε∈(1,2), then k0 and k1 can be calculated respectively. Figure 2 displays the mesh stiffness of tooth pairs for a gear drive with constant relative curvature. (Design parameters are in Tab. 1).
Design parameters for CRC gear drive.
2.2 Time-varying normal tooth loads
The path of contact, which passes through the pitch point, is defined as the set of the instant contact points of mating tooth profiles in the fixed coordinate system. As shown in Figure 3, Ʃc is the path of contact for engaged tooth profiles, Ʃp and Ʃg, which belong to the pinion and the gear, respectively. Op and Og are the centers of two gears, respectively. The point of P is the pitch point. rp and rg represent the radii of pitch circles, respectively. Suppose Ʃp and Ʃg engage at the point of C at some instant. Since P is the instantaneous center of velocity for the pinion and the gear, line PC must be the common normal of Ʃp and Ʃg, which represents the direction of normal load on tooth pair. Consequently, the curved path of contact causes the variation of the normal tooth load in direction. This effect can be counted in by introducing the geometric parameter αi, obtained from geometry analysis of tooth profiles. The magnitude of the normal load for the ith tooth pair can be expressed as
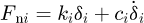 (4)
(4)
where ki is the time-varying mesh stiffness; ci is the damping coefficient for mesh; δi is the relative displacement in the direction of common normal of engaged tooth profiles, which is as follows 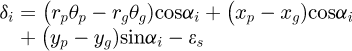 (5)
(5)
The dynamic transmission error (DTE) is defined as follows 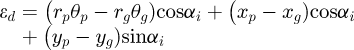 (6)
(6)
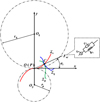 |
Fig. 3 Effect of curved path of contact on direction of normal tooth load. |
2.3 Six-degree-of-freedom model
A six-degree-of-freedom (6-DOF) dynamics model of the gear drive with curved path of contact is set up as displayed in Figure 4. Translation and rotation of engaged gears are considered, characterized by a generalized array ψ = (xp, yp, xg, yg, θp, θg)T. As shown in Figure 4, the driving torque Tp and resisting torque Tg are respectively applied to the pinion and gear, and ωp and ωg are their nominal angular velocity. Pair 0 and pair #1 are the meshing tooth pairs at some instant.
According to the Coulomb friction law, the magnitude of sliding friction force is proportional to the normal tooth load as follows 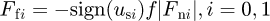 (7)
(7)
The sliding friction force is in the opposite direction of relative sliding velocity for engaged teeth. The moment arms for sliding friction forces of pinion and gear are respectively given by 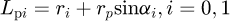 (8)
(8)
The moment arms for normal tooth loads of pinion and gear are respectively expressed as 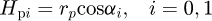 (10)
(10)
In equations (8) and (9), ri is the displacement from the pitch point to meshing point on the ith tooth pair. The sign of ri is defined as follows: for mesh points in quadrant III, ri < 0; for mesh points in quadrant I, ri > 0. Essentially, αi and ri are the geometric parameters that determine the position of the meshing point.
The governing equations for the translational degree of freedoms (DOFs) in x and y direction are respectively 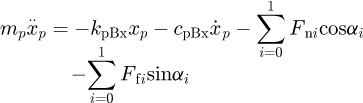 (12)
(12)
The governing equations for the rotational DOFs are 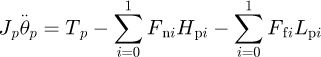 (16)
(16)
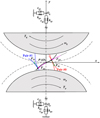 |
Fig. 4 6-DOF dynamics model of gear drive with curved path of contact. |
2.4 Friction coefficient in mixed EHL
Normally, gear drives run under the condition of mixed EHL. The friction coefficient of tooth surfaces varies as the teeth mesh, owing to continually changing lubrication conditions between contacting tooth surfaces. An engineering approach [18] is employed for computing the friction coefficient in mixed EHL line contact without need of performing extensive numerical simulations. The friction coefficient formula is as follows  (18)
(18)
In equation (18), the asperity load ratio La can be estimated as follows [19] 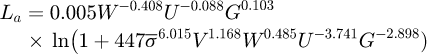 (19)
(19)
The limiting shear stress τlim is directly related to the lubricant's pressure [20], which is as follows 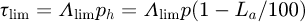 (20)
(20)
In the absence of lubricant specific properties, the Roelands formula [21] is often utilized to predict the average lubricant viscosity with reasonable accuracy. That is 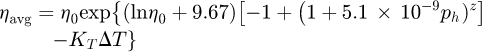 (21)
(21)
Where ΔT, the rise in temperature induced by the sliding in the mixed EHL regime, is estimated with the theory proposed by Tian and Kennedy [22]. Specifically, the flash temperature rise in the contact area of a moving square-shape heat source against a semi-infinite body is expressed as 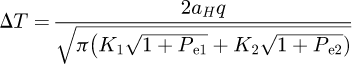 (22)
(22)
Here, total heat flux q in the contact area is related to average contact pressure, the asperity load ratio, limiting shear stress coefficient and relative sliding speed of engaged teeth, which is as follows 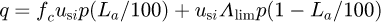 (23)
(23)
The expression of the central film thickness hc is provided by Masjedi and Khonsari [19] as follows 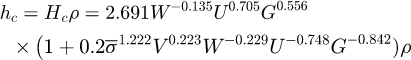 (24)
(24)
To sum up, the calculation procedure of friction coefficient in mixed EHL for engaged teeth is displayed as follows.
As can be seen from Figure 5, for calculation of friction coefficient, the relative curvature radius (ρ), relative sliding speed (usi) and normal contact load (Fni) need to be determined at mesh points. These results come from geometry analysis of tooth profiles and dynamics model. Finally, a tribo-dynamics integrated model is established for a spur gear drive with curved path of contact, which is displayed as Figure 6. Essentially, this treatment is a vigorous dynamics model of gear drive coupled with the friction coefficient model in mixed EHL. In fact, it also applies to involute gear drives, and the only difference is that the angle αi of involute gears is constant.
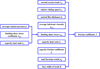 |
Fig. 5 Calculation procedure of friction coefficient. |
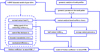 |
Fig. 6 Schematic of tribo-dynamics integrated model. |
3 Example
In this section an example is provided to illustrate the application of the above approach. The gear drive with constant relative curvature (CRC gear drive) [10] has some advantages over the involute spur gear drive, whose path of contact is a curve. The design parameters for the CRC gear drive are shown in Table 1. Material and lubricant parameters are shown in Table 2.
Material and lubricant parameters for CRC gear drive.
3.1 Model validation
To validate this model, a finite element model (FEM) and a multi-body dynamics model (MBDM) are built with commercial codes ABAQUS and ADAMS, respectively.
3.1.1 FEM
In view of the extensive computation time of dynamic FEM, a quasi-static FEM is constructed as illustrated in Figure 7. In this FEM, either of the engaged gears can only rotate about its own axis; Teeth are connected to the central reference points to maintain the kinematic coupling; Contact pairs are defined between engaged tooth surfaces. The main interaction properties are set as follows: Tangential behavior is frictionless; Normal behavior is “hard” contact; Elastic slip is “finite slip”. The simulation analysis consists of four analysis steps. First of all, the gear is completely fixed, and the pinion rolls by a tiny angle, which facilitates the convergence of the simulation. The second step is to apply the torque Tg (500 N·m) to the gear, and maintain the same boundary condition as step 1. The third step is to release the rotational degree of freedom for the gear. The last step is to add the constraint of angular displacement (1.2 rad) to the pinion. For the previous three steps, the analysis time duration and incremental step size are default values. For the last step, the analysis time duration is set to 1.2s, and the initial and maximum incremental step size are both 0.01s. C3D8R-type hexahedral elements are used for meshing, and the number of elements is 51264 totally.
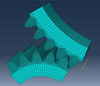 |
Fig. 7 Quasi-static FEM of CRC gear drive (mesh). |
3.1.2 MBDM
As displayed in Figure 8, the MBDM is built based on the three-dimension model of CRC gears. Either of the gear solids consists of the teeth and boss. The solid to solid contact pairs are defined for engaged teeth. The impact model is adopted to compute the normal contact loads of engaged teeth. The friction forces are not taken into consideration. There are two rigid bodies in the MBDM, which can only rotate about their respective axis. The input angular velocity of pinion is 10 rad/s, and the resisting torque on the gear is 500 Nm.
 |
Fig. 8 MBDM of CRC gear drive. |
3.1.3 Comparison of three models
The dominant advantage of the FEM is that the tooth deformation is counted in, but the accurate results depend on dense and refined meshes, which tend to consume a long computation time. Although solving the MBDM costs shorter time, it is troublesome to establish the model, especially to create contact pairs for potential engaged teeth. In addition, it is hard to introduce the friction coefficient model under mixed EHL into the FEM or MBDM due to difficulty in extracting the position information of contact points instantly. However, the 6-DOF model (6-DOFM) can be easily coupled with the friction coefficient model under mixed EHL.
For the 6-DOFM, the constant angular velocity of pinion is 10 rad/s, and the same resisting torque is applied to the gear. The governing equations are numerically solved through an algorithm for stiff problems (MATLAB ode15s). The results of normal tooth loads are compared with those of the FEM and MBDM. Also, the DTE is compared with that of MBDM. It's pointed out that the friction forces are not considered in this case.
As shown in Figure 9, three models provide the results of 2 consecutive tooth pairs. For the 6-DOFM, there are fluctuations round the key points of engagement such as Bg, Cp, Cg and Bp, while fluctuations of MBDM appear in double-tooth-contact period (DTCP). The overall trends of the two models are similar, and Fn in single-tooth-contact period (STCP) agrees well with each other. The average values of Fn in STCP are 7687N and 7690N, respectively. The results of 6-DOFM and MBDM are both larger than that of the FEM (7443N), because the FEM does not consider the impact in meshing in/out of teeth. It's worth noting that the contact ratio of the 6-DOFM is slightly lower than that of the other models. The reason is that geometric features-based contact model is used to simulate engagement of teeth in FEM and MBDM, and elastic deformation or penetration depth of contacting surfaces is allowed.
Figures 10a and 10b is the DTE of two models in time domain and frequency domain, respectively. Analysis in time domain indicates that the general tendencies of two plots are almost similar, though fluctuations appear in different positions and degrees. Additionally, either the maximum or the minimum is close to each other. As can be seen from Figure 10b, the mesh harmonics are both found at 36.63 Hz, 73.25 Hz, 109.87 Hz, and so on, nearly equal to gear mesh frequency (i ω, i=1,2,3,...). Besides, there are differences in the amplitudes for frequency orders to varying degrees. In essence, discrepancy in modeling method brings about differences in results.
 |
Fig. 9 Normal tooth loads of three models. |
 |
Fig. 10 Dynamic transmission error (MBDM, 6-DOFM). |
3.2 Results and discussion
In this section, the results of DTE, sliding friction forces, central film thickness and mechanical efficiency are analyzed in comparison with the involute gear drive. Both gear drives are featured with same module and tooth numbers, but the contact ratio of the involute gear drive is a little higher (εi = 1.66).
3.2.1 DTE
The DTE is the important index used to characterize transmission accuracy of a gear drive, which depends on the mesh stiffness and bearing stiffness. Figure 11 shows the results of DTE of two types of gear drives. It is apparent from the figure that the trends of DTE have a great deal in common. Especially, there is a sudden jump at the pitch point because the direction of friction force reverses. This phenomenon was also described in reference [13]. In terms of magnitude, the DTE of CRC gear drive is a little larger than that of the involute gear drive due to the lower mesh stiffness. In addition, once sliding friction forces are considered, the maximum and minimum of DTE tend to increase.
 |
Fig. 11 Dynamic transmission error. |
3.2.2 Sliding friction forces
Figure 12 illustrates the sliding friction forces of tooth pair #0 and tooth pair #1. According to Figure 12, sliding friction forces of two types of gear drives nearly have the same trends. For pair#1, the sliding friction force rises as the meshing point approaches the pitch point P. The HPSTC, Cp is an inflection point where the sliding friction force increases sharply. When the pair passes through the pitch point, the sign of sliding friction force changes in that the direction of relative sliding velocity reverses. From Cp to P or from P to Cg, the sliding friction force varies more slowly than in DTCP because of slow change of the normal tooth load. For pair#0, the sliding friction force decreases as the meshing point approaches Bp, the end point of meshing. In general, the trends of sliding friction force s are strongly dependent on those of normal tooth loads, though the frictional coefficients carry weight. Moreover, the average values of Ff0 and Ff1 are as follows: for CRC gear drive, Ff0c = 206N, Ff1c = 576N; for involute gear drive, Ff0i = 264N, Ff1i = 562N. On the whole, the sliding friction force of the involute gear drive is larger than that of the CRC gear drive.
Figure 13 demonstrates the sliding friction coefficients of tooth pair #0 and tooth pair #1. It can be observed from the figure that the CRC gear drive has a lower sliding friction coefficient. The reason is that the CRC gear drive is featured with the smaller relative curvature, lower relative sliding speed and higher entrainment speed[10]. Furthermore, no matter tooth pair #0 or tooth pair #1, the trend of sliding friction coefficient differs from each other. It is mainly because the relative curvature of the involute gear drive decreases as the contact point traverses, while that of the CRC gear drive is constant.
 |
Fig. 12 Sliding friction forces. |
 |
Fig. 13 Sliding friction coefficient. |
3.2.3 Central film thickness and entrainment speed
Figure 14 demonstrates the central film thickness of tooth pair #0 and tooth pair #1. The central film thickness hinges mainly on the normal tooth load, entrainment speed and relative curvature radius at the mesh point. For the CRC gear drive, the relative curvature radius at any mesh point is constant. Therefore, the central film thickness in DTCP is larger than that in STCP due to the smaller tooth normal load. From Cg to Bp, it rises with the decreasing of normal load and increasing of entrainment speed. Significantly, after the tooth pair passes through the pitch point, there is a rising tendency in the central film thickness, mainly due to decrease of the normal load (see Fig. 9). However, the relative curvature radius of the involute gear drive is always rising in entire engagement. For this reason, it presents a trend different from that of the CRC gear drive. In addition, whether pair #0 or pair#1, the central film thickness is significantly smaller than that of the CRC gear drive. Figure 15 displays the entrainment speed of pair #0 and pair #1. As can be seen from the figure, the entrainment speed of CRC gear drive is considerably higher than that of the involute gear drive because of the special tooth shape. The above analysis shows that the CRC gear drive has better lubrication performance than the involute gear drive, which undoubtedly improves the durability and efficiency of the gear drive.
 |
Fig. 14 Central film thickness. |
 |
Fig. 15 Entrainment speed. |
3.2.4 Mechanical efficiency of gear drives
On the condition that only frictional losses of gear drives are counted in, the instantaneous output power can be expressed as the difference between the input power and the frictional power losses. According to the approach by Xu [23], the mechanical efficiency (ME) of two types of gear drives is predicted as depicted in Figure 16.
The ME is influenced by relative sliding speed, friction forces and entrainment speed between engaged teeth. It can be seen from Figure 16 that the ME of two gear drives decreases firstly then increases, and it peaks at the pitch point because of the lowest relative sliding speed. But from P to Cg, the ME goes down. On the whole, the ME in STCP is higher than that in DTCP owing to fewer frictional power losses. The ME of the CRC gear drive is slightly higher than that of the involute gear drive during a meshing cycle, and the average efficiency are respectively 0.989 and 0.983.
 |
Fig. 16 Mechanical efficiency. |
4 Conclusions
A tribo-dynamics model of the gear drive with curved path of contact is proposed in this paper, including effects of directional variation of normal tooth loads, sliding friction and alternate meshing of single-double tooth pairs. The CRC gear drive is given as an example. The DTE, sliding friction forces, central film thickness and ME are analyzed. It can be concluded from above analysis as follows:
Directional variation of normal tooth loads can be taken into consideration by incorporating results from geometry analysis of tooth profiles into the dynamics model.
The transient lubrication properties in mixed EHL can be considered by calculating the transient friction coefficient regarding film thickness and asperity loads.
Compared to the involute gear drive, the CRC gear drive has the smaller sliding friction force, larger central film thickness, higher entrainment speed and higher mechanical efficiency.
The efficient tribo-dynamics integrated model is suitable to analyze dynamics characteristics of gear drives with curved path of contact comprehensively.
Nomenclature
φc: Angular displacement of pinion in one mesh cycle
tc: Duration of one mesh cycle
Zp, Zg: Tooth numbers of pinion and gear
rp, rg: Radii of pitch circles for pinion and gear
ωp: Nominal angular speed of pinion
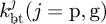 : Bending stiffness of tooth for pinion or gear
: Bending stiffness of tooth for pinion or gear
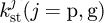 : Shear stiffness of tooth for pinion or gear
: Shear stiffness of tooth for pinion or gear
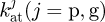 : Axial compressive stiffness of tooth for pinion or gear
: Axial compressive stiffness of tooth for pinion or gear
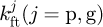 : Fillet foundation stiffness of tooth for pinion or gear
: Fillet foundation stiffness of tooth for pinion or gear
kct: Contact stiffness of single tooth pair
kt: Mesh stiffness of single tooth pair
ki: Mesh stiffness of ith tooth pair
Fni: Normal contact force of ith tooth pair
Jp, Jg: Inertia moments of pinion and gear
ξmi: Time-invariant mesh damping ratio
ci: Mesh damping of ith tooth pair, 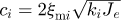
mp, mg: Mass of pinion and gear
θp, θg: Angular displacements of pinion and gear
αi: Included angle between common normal and x-axis of system oxy, 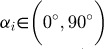
εs: Static transmission error, 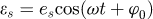
εd: Dynamic transmission error (DTE)
φ0: Initial phase of static transmission error
ω: Mesh frequency of gear drive, 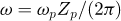
es: Amplitude of static transmission error
δi: Relative displacement along common normal of engaged tooth profiles
ε: Contact ratio of gear drive
ψ: Generalized array in 6-DOF dynamics model of gear drive
usi: Relative sliding speed of ith tooth pair
Ffi: Friction force of ith tooth pair
f: Friction coefficient of ith tooth pair
xp: Translational displacement of pinion in x-direction
xg: Translational displacement of gear in x-direction
yp: Translational displacement of pinion in y-direction
yg: Translational displacement of gear in y-direction
kpBx: Shaft-bearing stiffness of pinion in x-direction
kgBx: Shaft-bearing stiffness of gear in x-direction
kpBy: Shaft-bearing stiffness of pinion in y-direction
kgBy: Shaft-bearing stiffness of gear in y-direction
ξpBx: Shaft-bearing damping ratio of pinion in x-direction
ξgBx: Shaft-bearing damping ratio of gear in x-direction
ξpBy: Shaft-bearing damping ratio of pinion in y-direction
ξgBy: Shaft-bearing damping ratio of gear in y-direction
cpBx: Shaft-bearing damping of pinion in x-direction, 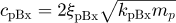
cpBy: Shaft-bearing damping of pinion in y-direction, 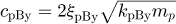
cgBx: Shaft-bearing damping of gear in x-direction, 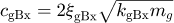
cgBy: Shaft-bearing damping of gear in y-direction, 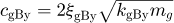
Lpi: Moment arm of friction force for ith tooth pair of pinion
Lgi: Moment arm of friction force for ith tooth pair of gear
ri: Displacement from pitch point to meshing point on ith tooth pair
Hpi: Moment arms for normal load for ith tooth pair of pinion
Hgi: Moment arms for normal load for ith tooth pair of gear
fc: Asperity friction coefficient
u1,2: Sliding speed of two contacting surfaces
w: Normal load per contact length, 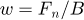
κ: Pressure–viscosity coefficient
U: Dimensionless speed number, 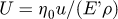
G: Dimensionless material number, 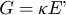
 : Dimensionless surface roughness number,
: Dimensionless surface roughness number, 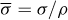
V: Dimensionless hardness number, 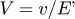
ρ: Relative curvature radius at mesh point
E1,2: Young's modulus of material
μ1,2: Poisson's ratio of material
E': Effective Young's modulus, 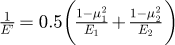
B: Effective face width of gear drive
Λlim: Limiting shear stress coefficient
p: Average contact pressure, p = Fn/(2aHB)
ph: Average hydrodynamic pressure
ηavg: Average lubricant viscosity
KT: Temperature-viscosity coefficient
q: Total heat flux in contact area
Pe1,e2: Peclet numbers for two contacting surfaces, 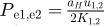
K1,2: Thermal conductivity of two contacting surfaces
Hc: Dimensionless central film thickness
Acknowledgments
This work is supported by the National Natural Science Foundation of China (Grant No. 52075238). It is also supported by National Key Laboratory of Science and Technology on Helicopter Transmission (Grant No. HTL-A-21G04).
References
- A. Dyson, H.P. Evans, R.W. Snidle, Wildhaber-Novikov circular arc gears: some properties of relevance to their design, Proc. Roy. Soc. London A 425, 341–363 (1989) [CrossRef] [Google Scholar]
- S.C. Yang, Mathematical model of a stepped triple circular-arc gear, Mech. Mach. Theory 44, 1019–1031 (2009) [CrossRef] [Google Scholar]
- T. Komori, Y. Ariga, S. Nagata, New gears profile having zero relative curvature at many contact points (logix tooth profile), J. Mech. Trans. Autom. Des. 112, 430–436 (1990) [CrossRef] [Google Scholar]
- B.E. Berlinger, J.R. Coulbourne, Gear form constructions[P], US Pat. 6101892 (2000) [Google Scholar]
- S.M. Luo, Y. Wu, J. Wang, The generation principle and mathematical models of a novel cosine gear drive, Mech. Mach. Theory 43, 1543–1556 (2008) [CrossRef] [Google Scholar]
- Y.C. Wu, K.Y. Chen, C.B. Tsay, Y. Ariga, Contact characteristics of circular-arc curvilinear tooth gear drives, J. Mech. Des. 131, 81003–81010 (2009) [CrossRef] [Google Scholar]
- H.L. Qi, H.X. Li, J.R. Wang, Y.C. Zhang, H. Huang, Transmission of point-line meshing gear, Int. J. Adv. Manufactur. Technol. 33, 845–855 (2007) [CrossRef] [Google Scholar]
- G. Hlebanja, S-gears for wind power turbine operating conditions, Mach. Des. 4, 123–130 (2012) [Google Scholar]
- J. Wang, L. Hou, S.M. Luo, R.Y. Wu., Active design of tooth profiles using parabolic curve as the line of action, Mech. Mach. Theory 67, 47–63 (2013) [CrossRef] [Google Scholar]
- L. Liu, F. Meng, J.L. Ni, A novel non-involute gear designed based on control of relative curvature, Mech. Mach. Theory 140, 144–158 (2019) [CrossRef] [Google Scholar]
- K. Huang, T. Wang, Dynamic features of a micro segment gear system, Chin. J. Vib. Shock 37, 248–253 (2018) [Google Scholar]
- M. Vaishya, R. Singh, Strategies for modeling friction in gear dynamics, J. Mech. Des. 125, 383–393 (2003) [CrossRef] [Google Scholar]
- H. Song, R. Gunda, R. Singh, Effect of sliding friction on the dynamics of spur gear drive with realistic time-varying stiffness, J. Sound Vibr. 301, 927–949 (2007) [CrossRef] [Google Scholar]
- G. Liu, R.G. Parker, Impact of tooth friction and its bending effect on gear dynamics, J. Sound Vibr. 320, 1039–1063 (2009) [CrossRef] [Google Scholar]
- S. Li, A. Kahraman, Influence of dynamic behaviour on elastohydrodynamic lubrication of spur gears, Proc. Inst. Mech. Eng. J 225, 740–753 (2011) [CrossRef] [Google Scholar]
- P. Fietkau, B. Bertsche, Efficient simulation of gear contacts including transient elastohydrodynamic effects, Trans. ASME 135, 031502-1-9 (2013) [Google Scholar]
- K.L. Johnson, Contact Mechanics [M]. Cambridge University Press, Cambridge, MA (1985) [Google Scholar]
- M. Masjedi, M.M. Khonsari, An engineering approach for rapid evaluation of traction coefficient and wear in mixed E.H.L., Tribol. Int. 92, 184–190 (2015) [CrossRef] [Google Scholar]
- M. Masjedi, M.M. Khonsari, Film thickness and asperity load formulas for line-contact elastohydrodynamic lubrication with provision for surface roughness, J. Tribol. 134, 11503–11512 (2012) [CrossRef] [Google Scholar]
- S.S. Bair, C. McCabe, High-pressure rheology for quantitative elastohydrodynamics[M], 1st edn., Elsevier, Amsterdam, Boston, 2007 [Google Scholar]
- C.J.A. Roelands, Correctional aspects of the viscosity-temperature-pressure relationship of lubricating oils[M], Druk, V.R.B., Groningen, Netherlands (1966) [Google Scholar]
- X.F. Tian, F.E. Kennedy, Maximum and average flash temperatures in sliding contacts, Trans. ASME 116, 167–174 (1994) [CrossRef] [Google Scholar]
- H. Xu, A. Kahraman, N.E. Anderson, D.G. Maddock, Prediction of mechanical efficiency of parallel-axis gear drives, Trans. ASME 129, 58–68 (2007) [CrossRef] [Google Scholar]
Cite this article as: Lei Liu, Jiale Ni, An efficient dynamics model of spur gear drive with curved path of contact in mixed elastohydrodynamic lubrication, Mechanics & Industry 23, 10 (2022)
All Tables
All Figures
 |
Fig. 1 Contact pattern in spur gear drive with curved path of contact. |
| In the text | |
 |
Fig. 2 Mesh stiffness of tooth pairs. |
| In the text | |
 |
Fig. 3 Effect of curved path of contact on direction of normal tooth load. |
| In the text | |
 |
Fig. 4 6-DOF dynamics model of gear drive with curved path of contact. |
| In the text | |
 |
Fig. 5 Calculation procedure of friction coefficient. |
| In the text | |
 |
Fig. 6 Schematic of tribo-dynamics integrated model. |
| In the text | |
 |
Fig. 7 Quasi-static FEM of CRC gear drive (mesh). |
| In the text | |
 |
Fig. 8 MBDM of CRC gear drive. |
| In the text | |
 |
Fig. 9 Normal tooth loads of three models. |
| In the text | |
 |
Fig. 10 Dynamic transmission error (MBDM, 6-DOFM). |
| In the text | |
 |
Fig. 11 Dynamic transmission error. |
| In the text | |
 |
Fig. 12 Sliding friction forces. |
| In the text | |
 |
Fig. 13 Sliding friction coefficient. |
| In the text | |
 |
Fig. 14 Central film thickness. |
| In the text | |
 |
Fig. 15 Entrainment speed. |
| In the text | |
 |
Fig. 16 Mechanical efficiency. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.