| Issue |
Mechanics & Industry
Volume 22, 2021
|
|
|---|---|---|
| Article Number | 47 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/meca/2021044 | |
| Published online | 17 November 2021 | |
Regular Article
High load capacity spur gears with conchoidal path of contact
1
E.O. Paton Electric Welding Institute of the National Academy of Sciences of Ukraine, 11 K. Malevycha st., Kyiv 03150, Ukraine
2
National Aviation University, Department of Engineering Science, 1 L. Huzara ave., Kyiv 03058, Ukraine
3
Bialystok University of Technology, Faculty of Mechanical Engineering, 45C Wiejska st., Bialystok 15351, Poland
* e-mail: y.tsybrii@pb.edu.pl
Received:
22
September
2020
Accepted:
13
October
2021
The present study is devoted to investigation of spur gears with a conchoidal path of contact and a convex-convex contact between teeth. The load capacity and energy efficiency were evaluated using both theoretical and experimental approaches. The theoretical analysis showed that the conchoidal gear pairs are 5–21% stronger in terms of contact stress and have similar energy efficiency as compared to the involute gear pairs of the same configuration. Experiments were conducted on a gear test rig. Its energy efficiency was determined by measuring the active power of the motor driving the pinion shaft and controlling the torque at the gear shaft. The load capacity of the tested gear pair was estimated by analysing changes in the energy efficiency. It was found that the conchoidal gear pair has more than 20% higher load capacity and slightly higher energy efficiency, which agrees well with the mentioned theoretical results. Thereby, the study concludes a substantially higher load capacity of the conchoidal gears compared to the traditional involute ones.
Key words: Spur gears / involute gears / conchoidal path of contact / load capacity / contact strength / energy efficiency
© P. Tkach et al., Published by EDP Sciences 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Gears are widely used to transmit motion and energy in mechanical systems. It is difficult to imagine a modern transport machine that does not include gear trains. The most commonly used gears have teeth with an involute active profile generated by straight lines. The set of instantaneous contact points between such teeth forms a straight path of contact. The advantages of involute gears include high manufacturability, relatively small sensitivity to centre distance errors and simplicity of the reference profile. However, relatively large curvatures of the mating teeth result in large contact stresses, which strongly limits the load capacity of involute gears. Therefore, development of non-involute gear drives has a significant scientific and practical interest.
Helical gears with a circular-arc tooth profile were proposed by Wildhaber [1] and Novikov [2], subsequently called ‘Wildhaber-Novikov gears’. Novikov's idea is that the contact between gears should take place at a point moving along a tooth. The active profile of one tooth is generated by a convex arc, while that of the mating tooth is generated by a concave arc of a slightly larger radius. Accordingly, the convex-concave contact between teeth is characterised by a reduced curvature, which leads to smaller contact stresses. But a serious disadvantage of Wildhaber-Novikov gears can be found in increased bending stresses in teeth due to the point contact. A comprehensive analysis of this type of gears was performed in the studies [3,4].
Wildhaber-Novikov concept of gearing served as the basis for the development of various circular-arc tooth profiles. One of the successful technical solutions is the application of double circular-arc tooth profile helical gears [5] (p. 158). The reference profile for generating teeth active profiles is composed of two conjugated circular arcs: convex addendum arc and concave dedendum arc. Accordingly, the convex addendums interact with the concave dedendums of the respective pinion and gear teeth. The parameters of two circular arcs are sought to minimise both contact stresses and bending stresses in teeth [6]. The other known technical solutions include (but are not limited to) gears with basic rack of combined circular and involute profile [7], circular-arc tooth pinion on involute tooth gear [8], point-line meshing gears [9], circular-arc curvilinear tooth gears [10], stepped triple circular-arc tooth gears [11], double circular-arc tooth gears modified by tooth end relief with helix [12], double circular-arc tooth gears optimised for harmonic drives [13].
As concerns spur gears, various alternative tooth shapes were proposed to improve the load capacity of gear drives. It is important to name, for instance, gears with zero relative curvature at many contact points [14], gears with linear profile modification [15], gears with quadratic parametric tooth profile [16], tooth profile relief design gears [17], asymmetric tooth gears [18], gears designed by usage of NURB deviation function technique [19], gears designed by B-spline curve fitting and sweep surface modelling [20], gears with multi-segment path of contact [21], cosine tooth gears [22], s-gears designed for wind power turbine operating conditions [23], gears with parabolic path of contact [24], gears with a constant relative curvature [25], gears with a circular arc contact path [26]. Although the mentioned technical solutions were shown to be effective for particular applications and operating conditions, their widespread implementation is limited by the difficulties related to manufacturing complex-shaped teeth.
A relatively simple double circular-arc reference profile for spur gears was proposed in the study [27]. The path of contact of these gears represents a conchoid of Nicomedes. Therefore, they are sometimes referred to as ‘conchoidal path-of-contact gears’ or ‘conchoidal gears’. The study [28] investigated the conchoidal gears with convex-concave contact between teeth and concluded their better meshing and performance characteristics compared to the involute gears. Their disadvantage, however, is an increased sensitivity to manufacturing and mounting errors [29] (p. 33). The study [30] showed that the tooth profiles of the conchoidal gears can be designed to allow a convex-convex contact, which can potentially eliminate the mentioned above disadvantage. To the best authors' knowledge, this potentially promising type of conchoidal gears has not been investigated in terms of load capacity and energy efficiency yet. With this in mind, the purpose of the present study was to theoretically and experimentally investigate the load capacity of the conchoidal path-of-contact spur gears with convex-convex contact between teeth as compared to the traditional involute gears.
2 Theory
2.1 Geometry of the conchoidal gears
Figure 1 presents a geometric description of the conchoidal gears under consideration. Figure 1a shows the generating surface defined in a coordinate system xgOgyg. Figure 1b introduces the pitch circles of the pinion 1 and gear 2 and the path of contact. Note that the coordinate systems x1O1y1 and x2O2y2 are aligned with the respective pinion 1 and gear 2, whereas XOY is the fixed coordinate system with centre O at the pitch point.
The generating surface is based on the reference profile shown in Figure 1c. The curves OgA and OgB form the active profile of a tooth, while 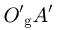 and
and  form the active profile of the adjacent tooth. The curve AA′ is responsible for generation of the tooth root fillet.
form the active profile of the adjacent tooth. The curve AA′ is responsible for generation of the tooth root fillet.
The coordinates of the tooth active profile are expressed separately for the curve OgA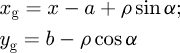 (1)curve OgB
(1)curve OgB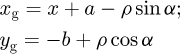 (2)curve
(2)curve 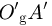
 (3)and curve
(3)and curve 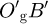
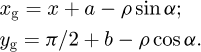 (4)
(4)
Here α is the reference profile angle varying from αw to αmax; αw is the reference profile angle at the pitch line (point Og); αmax is the maximum reference profile angle (points A and B); ρ is the profile circle radius; x is the reference profile shift coefficient; parameters a and b are given by
It is important to note that equations (1)–(4) and the following equations incorporating geometric parameters are normalised for the module m equal to 1 mm.
Assume that the reference profile is symmetrical. Then it is sufficient to consider the active profile formed only by the curves OgA and OgB. The coordinates of the active profile, given by equations (1) and (2), are represented in a concise form: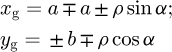 (5)where the upper and lower signs stand for the curves OgA and OgB, respectively.
(5)where the upper and lower signs stand for the curves OgA and OgB, respectively.
In the meshing of the generating surface and a tooth being generated, the vector of the relative velocity must be perpendicular to the line normal to the generating surface at the contact point [6]. As applied to the conchoidal gears, this condition allows writing the equation of meshing as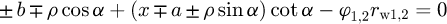 (6)which represents the relationship between α and the angle ϕ1,2 of rotation of the pinion/gear. Here rw1,2 is the pitch circle radius of the pinion/gear. As the pitch circles mesh without sliding, it is true that ϕ1rw1 = ϕ2rw2.
(6)which represents the relationship between α and the angle ϕ1,2 of rotation of the pinion/gear. Here rw1,2 is the pitch circle radius of the pinion/gear. As the pitch circles mesh without sliding, it is true that ϕ1rw1 = ϕ2rw2.
The equation of the path of contact can be formulated in the coordinate system XOY based on equations (5) and (6) in the form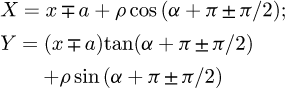 which coincides with the expression for the conchoid of Nicomedes with angle (α + π ± π/2) and parameters (x ∓ a) and ρ.
which coincides with the expression for the conchoid of Nicomedes with angle (α + π ± π/2) and parameters (x ∓ a) and ρ.
From equation (6) one can also derive the equations for the pinion active profiles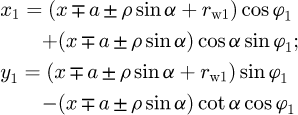 (7)
(7)
and gear active profiles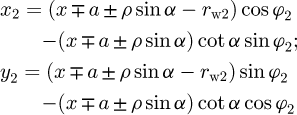 (8)in the respective coordinate systems x1O1y1 and x2O2y2.
(8)in the respective coordinate systems x1O1y1 and x2O2y2.
Equations (6)–(8) allow thus finding the coordinates of the contact point and the points of the active profiles for specified values of ϕ1 and ϕ2.
Depending on the geometric parameters, the contact between teeth in a conchoidal gear pair can be of convex-concave or convex-convex type. The present study focusses on investigation of the convex-convex contact which takes place under the condition [30] that
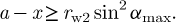
The following analysis requires specification of the parameters of the simulated reference profiles and gear pairs. The angle αw of 20° is the most common, while it can be 25° or even 28° in special gear transmissions [31] (p. 75, 143). Table 1 describes three reference profiles, code-named as ‘α20’, ‘α25’ and ‘α28’, with αw close to the mentioned values.
Figure 2 shows the teeth profiles of the pinion 1 and gear 2 generated by the reference profiles of Table 1. The profiles of the pinion 1 are determined due to equation (7) in the coordinate system x1O1y1 (solid lines), while the profiles of the gear 2 are determined due to equation (8) in the coordinate system x2O2y2 (dashed lines). In both cases, the values of ϕ1,2 are calculated by equation (6). For the sake of clarity, the profiles of the gear 2 are shown not in its own coordinate system but are meshed with the respective profiles of the pinion at ϕ1 = 0. The geometry of the teeth corresponds to u = z2/z1 = 72/18 and is normalised for m = 1 mm.
The shift of the reference profile has a significant influence on the performance of the gear pair. Table 2 presents three simulated cases: zero shift (‘x0’), 0.3 shift (‘x0.3’) and 0.5 shift (‘x0.5’).
Finally, Table 3 presents the parameters of the simulated gear pairs and operating conditions. Two gear pairs, code-named as ‘u2.4’ and ‘u4’, have the same parameters except for the number z1 of the pinion teeth and, accordingly, gear ratio u = z2/z1.
 |
Fig. 1 Geometry of conchoidal gears: (a) generating surface; (b) pinion 1 and gear 2; (c) reference profile. |
Parameters of the simulated reference profiles normalised for m = 1 mm.
 |
Fig. 2 Geometry of the teeth active profiles of the pinion 1 and gear 2. |
Shift coefficient x of the simulated reference profile normalised for m = 1 mm.
Parameters of the simulated gear pairs and operating conditions.
2.2 Contact strength
The instantaneous mechanical contact of two gear teeth is often treated as the contact between two cylinders with parallel axes. The relationship between the stress σH and normal force Fn in the contact zone is then defined by the Hertz equation. If the pinion and gear are made of the same steel with elastic modulus E, this equation takes the form [5]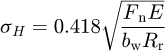 (9)where Rr is the reduced curvature radius of the active profiles of the mating teeth at the contact point; bw is the effective face width.
(9)where Rr is the reduced curvature radius of the active profiles of the mating teeth at the contact point; bw is the effective face width.
For the conchoidal gear pair, it yields from equations (5)–(8) that
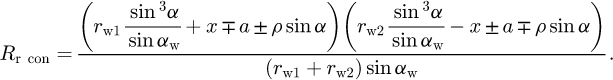
On the other hand, following the study [28], one can derive a similar expression for the involute gear pair: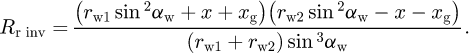
The normal force Fn in the contact zone is expressed via the pinion torque T1 as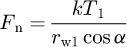 (10)where k = 1 for one-pair contact and k = 0.5 for double-tooth contact.
(10)where k = 1 for one-pair contact and k = 0.5 for double-tooth contact.
Substitution of equation (10) into equation (9) leads to the equation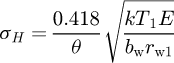 (11)
(11)
where the coefficient θ given by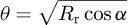 depends solely on the geometry of the active profiles. According to equation (11), θ is inverse proportional to σH and, thereby, can serve as the measure of contact strength.
depends solely on the geometry of the active profiles. According to equation (11), θ is inverse proportional to σH and, thereby, can serve as the measure of contact strength.
Based on the expressions of Rr con and Rr inv above, one easily finds θ for the conchoidal gear pair:
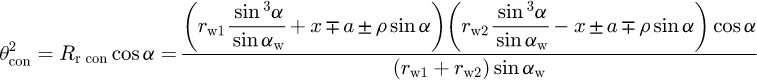 (12) and for the involute gear pair:
(12) and for the involute gear pair:
 (13)
(13)
Note that θcon of equation (12) is a function of α, while θinv of equation (13) is a function of xg.
Figure 3 illustrates the variation ranges of the ratio θcon/θinv calculated by equations (12) and (13) for the reference profiles and gear pairs specified in Tables 1–3. The limit values of each variation range correspond to the limit points of the path of contact. It is seen that for all combinations under consideration, θcon/θinv is noticeably larger than 100%. The lower limit of θcon/θinv varies between 105% and 121%, implying that the conchoidal gear pairs have 5–21% higher contact strength compared to the involute gear pairs of the same configuration. An exceptional case is ‘α20 u4 x0’, implying αw = 20°, u = 4 and x = 0, at which the upper limit of θcon/θinv is about 200%. This case is characterised by a close to zero curvature radius at the tooth dedendum of the pinion and, therefore, is eliminated from consideration. It is notable that θcon/θinv decreases substantially as αw increases.
 |
Fig. 3 Ratio between contact strength coefficients θcon and θinv. |
2.3 Energy efficiency
The active profiles of the mating teeth slide relative each other at the contact point with velocity υg. This is inevitably accompanied by the friction process which is characterised by friction coefficient μ. Introduce the energy efficiency of a gear pair as follows: (14)where ω1 is the angular velocity of the pinion; ϕ11 and ϕ12 are the angles of the pinion rotation which correspond to the start and end of the meshing phase. The start contact point and end contact point in the meshing of the pinion and gear are defined in the generating process by the points of the reference profile with angle αmax1 at ϕ1 = ϕ11 and angle αmax2 at ϕ1 = ϕ12, respectively. The values of αmax1 and αmax2 are found by the equations below:
(14)where ω1 is the angular velocity of the pinion; ϕ11 and ϕ12 are the angles of the pinion rotation which correspond to the start and end of the meshing phase. The start contact point and end contact point in the meshing of the pinion and gear are defined in the generating process by the points of the reference profile with angle αmax1 at ϕ1 = ϕ11 and angle αmax2 at ϕ1 = ϕ12, respectively. The values of αmax1 and αmax2 are found by the equations below:
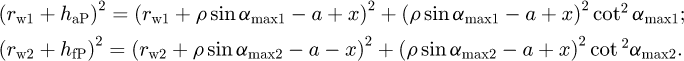
The integral term in equation (14) indicates the fraction of the input power that transforms into friction heat over one meshing phase from ϕ11 to ϕ12.
For the conchoidal gear pair, the sliding velocity is derived from equations (5) and (6) as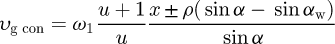 while for the involute gear pair, it can be expressed in our notation as
while for the involute gear pair, it can be expressed in our notation as
For steel-on-steel gear teeth contacts, the friction coefficient μ is well approximated by the empirical function [32,33] (15)where BHN is the Brinell hardness number; Ra is the roughness parameter; ν is the oil kinematic viscosity; υΣ is the sum of the velocity components of the active profiles at the contact point perpendicular to the line of contact [31] (p. 182). The quantities in equation (15) should be specified in the following units of measurements: BHN and E in the same units; Fn in N; bw in mm; Rr and Ra in cm; ν in mm2/s; υg and υΣ in cm/s.
(15)where BHN is the Brinell hardness number; Ra is the roughness parameter; ν is the oil kinematic viscosity; υΣ is the sum of the velocity components of the active profiles at the contact point perpendicular to the line of contact [31] (p. 182). The quantities in equation (15) should be specified in the following units of measurements: BHN and E in the same units; Fn in N; bw in mm; Rr and Ra in cm; ν in mm2/s; υg and υΣ in cm/s.
The formula to calculate υΣ for the conchoidal gear pair is obtained from equations (5) and (6) in the form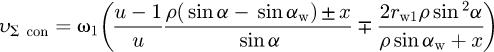 while for the involute gear pair, it reads
while for the involute gear pair, it reads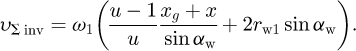
Figure 4 shows the values of the ratio between the energy efficiencies ηcon and ηinv calculated by equation (14) for the respective conchoidal and involute gear pairs. It is seen that ηcon is up to 0.1% larger than ηinv for all considered combinations, suggesting that the conchoidal gear pairs have similar energy efficiency as the involute gear pairs of the same configuration. This result is explained by the fact that μ of equation (15) takes a smaller value in the case of conchoidal gear pair, which is due to the inequalities υΣ con > υΣ inv and Rr con > Rr inv.
 |
Fig. 4 Ratio between energy efficiencies ηcon and ηinv. |
3 Experimental study
The foregoing theoretical analysis showed that the conchoidal gear pairs have a substantially higher contact strength and similar energy efficiency if compared to the involute gear pairs with the same parameters. These findings should undergo experimental validation to be accepted. This section describes an experimental study of the conchoidal and involute gear pairs in terms of the mentioned characteristics.
3.1 Tooth-cutting tool
A hob cutter was designed and manufactured for cutting conchoidal gear pairs. It was made of P18 steel due to GOST 19265-73 (EN X75WCrV18-4-1) and heat treated to Rockwell hardness HRC 65. The parameters of the hob cutter are presented in Table 4, while its tooth profile is schematically shown in Figure 5. The parameters of the reference profile were calculated using the formulae given in Table 5.
Hob cutter parameters.
 |
Fig. 5 Hob cutter tooth profile. |
Reference profile parameters.
3.2 Tested gear pairs
Using the hob cutter, 3 conchoidal gear pairs were manufactured. Further 3 involute gear pairs were manufactured using a standard hob cutter of the same module. All gears were cut out of 40X steel (EN 41Cr4) due to GOST 4543-71 364. Table 6 presents its mechanical properties. The conchoidal and involute gear pairs had the same configuration presented in Table 7. Note that they were manufactured with the reference profile shift corresponding to ‘x0.5’ (see Tab. 2).
The pinion and gear of the tested gear pair (conchoidal or involute) were installed on the shafts supported by bearings inside a gear box. An oil bath lubrication method with natural convection was used. The gears were lubricated by an AK15 motor oil. The level of oil in the gear box was regularly monitored.
Gear steel mechanical properties.
Gear pair parameters.
3.3 Gear test rig
The tests were carried out using a gear test rig shown in Figure 6. The principal units of the test rig were an electric motor, the gear box with the tested gear pair inside and an electromagnetic powder brake. The motor of rated power 15 kW applied torque T1 to the pinion shaft and drove it with angular velocity ω1 of 153.9 rad/s. The brake allowed controlling the torque T2 at the gear shaft by measuring displacements of an elastic element. The motor, gear box and brake were dead mounted to a massive basement with bolts. The shafts of the mentioned units were connected by flexible couplings. An accurate alignment of the shafts was provided. The measurement system of the test rig allowed measuring the active power P = T1ω1 of the motor, the gear torque T2 and the temperature ϑ of the oil in the gear box.
 |
Fig. 6 Gear test rig. |
3.4 Research methodology
Each gear pair was tested according to a multi-step procedure developed in the Central Scientific Research Institute of Machine Building and Metalworking (former Soviet Union) intended for conventional gear transmissions, as described in Table 8.
Zero step was a 2-hour running-in of the gear pair with the brake off (idle mode). At each next loading step, the gear torque T2 was increased so that the corresponding pinion torque T1 increased by 0.2[T1], where [T1] is the allowable pinion torque. The value of [T1] was determined based on equation (9) with account of different factors: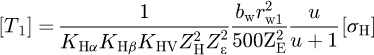 where [σH] is the allowable contact stress (see Tab. 6); KHα is the factor of non-uniform load distribution between the teeth; KHβ is the factor of non-uniform load distribution along the contact lines; KHV is the factor of the internal dynamic load in the meshing; ZE is the factor in view of the mechanical properties of the gears,
where [σH] is the allowable contact stress (see Tab. 6); KHα is the factor of non-uniform load distribution between the teeth; KHβ is the factor of non-uniform load distribution along the contact lines; KHV is the factor of the internal dynamic load in the meshing; ZE is the factor in view of the mechanical properties of the gears, 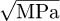 ; ZH is the factor in view of the shape of the mating teeth surfaces at the pitch point; Zϵ is the factor in view of the total length of the contact lines. In the equation above, [T1] is in Nm, [σH] is in MPa, bw and rw1 are in mm.
; ZH is the factor in view of the shape of the mating teeth surfaces at the pitch point; Zϵ is the factor in view of the total length of the contact lines. In the equation above, [T1] is in Nm, [σH] is in MPa, bw and rw1 are in mm.
At the loading steps 1 to 4, the gear pair was tested for 8 hours per day, with total duration of 24 hours. Accordingly, the state of the active surfaces of the gears was examined after each 8 test hours. After the loading step 4, the used oil was drained from the gear box, the gear box and the components inside it were cleaned, and fresh oil was added. At the loading steps 5 and 6 with respective loads [T1] and 1.2 [T1], the gear pair was tested for 8 hours per day, with total number of pinion cycles of NH lim and 1.5NH lim, respectively. Here NH lim is the base number of cycles (see Tab. 6).
The energy efficiency ηe of the test rig was determined from the known values of the motor active power P, pinion angular velocity ω1 and gear torque T2 as follows:
It is noteworthy that ηe represents the product of the energy efficiencies of all units of the test rig, including the gear box. Since the test rig operated under the same kinematic and loading conditions regardless of gear pair type, one can compare the energy efficiencies of the conchoidal and involute gear pairs based on the ratio between the values of ηe con and ηe inv obtained by testing the respective conchoidal and involute gear pairs.
Experimental multi-step procedure.
4 Results and discussion
The experimental data are shown in Figures 7 and 8. Each point indicates the average stationary value obtained from testing 3 gear pairs at a specific loading step.
Figure 7 shows the dependence of the energy efficiencies ηe con and ηe inv on the pinion torque T1. It is seen that ηe con is systematically 0.1–0.2% larger than ηe inv, implying that the conchoidal gear pair is slightly more energy efficient than the involute one. The value of ηe inv at T1 =37.2 Nm, however, is not in line with the general trend. An after-test visual examination showed that the active surfaces of the involute gears were subjected to severe pitting, whereas the conchoidal gears were damaged insignificantly. This allows to explain the unexpected decrease in ηe inv at T1 = 37.2 Nm.
The data presented in Figure 7 suggest that T1 of about 31 Nm corresponds to the load capacity of the involute gear pair. On the other hand, the stable growth of ηe con allows stating that the load capacity of the conchoidal gear pair is as minimum as 37.2 Nm, which is 20% larger. This correlates well with the theoretical finding that the conchoidal gear pairs have 5–21% higher contact strength compared to the involute gear pairs of the same configuration.
Figure 8 shows the influences of T1 on the gear box oil temperatures ϑcon and ϑinv measured for the respective conchoidal and involute gear pairs. According to the presented values, ϑinv is substantially larger than ϑcon, i.e., the involute gear pair generates more friction heat than the conchoidal one. This confirms qualitatively the results of Figure 7. It is also seen that the increase in ϑinv is large at T1 = 37.2 Nm, which is in agreement with the behaviour of ηe inv.
For the nominal mode of T1 = 31 Nm, ϑcon is 17% smaller than ϑinv (see Fig. 8). For the sake of comparison, flash temperatures arising in the contact points of the tested gear pairs operating in the nominal mode were simulated based on Blok's formula [5]. The simulations show that as compared to the involute gear pair, the flash temperature in the conchoidal gear pair is 27% lower for the pinion tooth addendum on gear tooth dedendum contact, 56% lower for the pinion tooth dedendum on gear tooth addendum contact, and on average 20% higher for the teeth contact in the vicinity of the pitch point which is about 0.4m in height.
 |
Fig. 7 Gear test rig energy efficiency ηe vs pinion torque T1. |
 |
Fig. 8 Gear box oil temperature ϑ vs pinion torque T1. |
5 Conclusion
The conchoidal path-of-contact spur gears of convex-convex contact type were systematically investigated regarding their load capacity and energy efficiency. The theoretical analysis conducted for different values of the reference profile parameters and gear ratio showed that the conchoidal gear pairs are 5–21% stronger in terms of contact stress and have similar energy efficiency if compared to the traditional involute gear pairs of the same configuration. These findings were experimentally validated using a gear test rig in which the energy efficiency was determined by measuring the active power of the motor driving the pinion shaft for a controlled value of the torque at the gear shaft. The load capacity of the tested gear pair was estimated by analysing the behaviour of the energy efficiency under intensifying loading conditions. It was found that the load capacity of the conchoidal gear pair is higher by more than 20%, while its energy efficiency is slightly higher. A good agreement between the obtained theoretical and experimental results confirms a substantially higher load capacity of the conchoidal gears.
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Notation
x: Reference profile shift coefficient
xgOgyg: Coordinate system aligned with reference profile
αw: Reference profile angle at pitch line
αmax: Maximum reference profile angle
η: Simulated energy efficiency of gear pair
ηe: Measured energy efficiency of gear test rig
θ: Contact strength coefficient
[σH]: Allowable contact stress
p: Related to reference profile
0: Related to tooth-cutting tool
1,2: Related to pinion and gear
con: Related to conchoidal gear pair
inv: Related to involute gear pair
References
- E. Wildhaber, Helical gearing, patent US 1601750, 1926 [Google Scholar]
- M.L. Novikov, Gear transmissions and cam mechanisms with a point meshing system, patent SU109113, 1956 (in Russian) [Google Scholar]
- F.L. Litvin, C.B. Tsay, Helical gears with circular arc teeth: simulation of conditions of meshing and bearing contact, J. Mech. Trans. Autom. 107, 556–564 (1985) [CrossRef] [Google Scholar]
- A. Dyson, H.P. Evans, R.W. Snidle, Wildhaber-Novikov circular arc gears: geometry and kinematics, Proc. R. Soc. A 403, 313–340 (1986) [Google Scholar]
- V.N. Kudrjavcev, J.A. Derzhavec, E.G. Gluharev, Design and calculation of reduction gears, Mashinostroenie, Leningrad, 1971 (in Russian) [Google Scholar]
- F.L. Litvin, J. Lu, Computerized simulation of generation, meshing and contact of double circular-arc helical gears, Math. Comput. Model. 18, 31–47 (1993) [CrossRef] [Google Scholar]
- Y. Ariga, S. Nagata, Load capacity of a new W-N gear with basic rack of combined circular and involute profile, J. Mech. Trans. Autom. 107, 565–572 (1985) [CrossRef] [Google Scholar]
- C.B. Tsay, Z.H. Fong, Computer simulation and stress analysis of helical gears with pinion circular arc teeth and gear involute teeth, Mech. Mach. Theory 26, 145–154 (1991) [CrossRef] [Google Scholar]
- Q. Luo, H. Li, J. Wang, Y. Zhang, H. Huang, Transmission of point-line meshing gear, The Int. J. Adv. Manufactur. Technol. 33, 845–855 (2007) [CrossRef] [Google Scholar]
- Y.C. Wu, K.Y. Chen, C.B. Tsay, Y. Ariga, Contact characteristics of circular-arc curvilinear tooth gear drives, J. Mech. Des. 131, 181003 (2009) [Google Scholar]
- S.C. Yang, Mathematical model of a stepped triple circular-arc gear, Mech. Mach. Theory 44, 1019–1031 (2009) [CrossRef] [Google Scholar]
- H. Zhang, L. Hua, X. Han, Computerized design and simulation of meshing of modified double circular-arc helical gears by tooth end relief with helix, Mech. Mach. Theory 45, 46–64 (2010) [CrossRef] [Google Scholar]
- X. Chen, Y. Liu, J. Xing, S. Lin, W. Xu, The parametric design of double-circular-arc tooth profile and its influence on the functional backlash of harmonic drive, Mech. Mach. Theory 73, 1–24 (2014) [CrossRef] [Google Scholar]
- T. Komori, Y. Ariga, S. Nagata, A new gears profile having zero relative curvature at many contact points (logiX tooth profile), J. Mech. Des. 112, 430–436 (1990) [CrossRef] [Google Scholar]
- C. Lee, H.H. Lin, F.B. Oswald, D.P. Townsend, Influence of linear profile modification and loading conditions on the dynamic tooth load and stress of high-contact-ratio spur gears, J. Mech. Des. 113, 473–480 (1991) [CrossRef] [Google Scholar]
- M.H. Tsai, Y.C. Tsai, Design of high-contact-ratio spur gears using quadratic parametric tooth profiles, Mech. Mach. Theory 33, 551–564 (1998) [CrossRef] [Google Scholar]
- N. Yildirim, R.G. Munro, A systematic approach to profile relief design of low and high contact ratio spur gears, Proc. Inst. Mech. Eng. C 213, 551–562 (1999) [CrossRef] [Google Scholar]
- A. Kapelevich, Geometry and design of involute spur gears with asymmetric teeth, Mech. Mach. Theory 35, 117–130 (2000) [CrossRef] [Google Scholar]
- T. Yeh, D.C.H. Yang, S.H. Tong, Design of new tooth profiles for high-load capacity gears, Mech. Mach. Theory 36, 1105–1120 (2001) [CrossRef] [Google Scholar]
- S. Barone, Gear geometric design by B-spline curve fitting and sweep surface modelling, Eng. Comput. 17, 66–74 (2001) [CrossRef] [Google Scholar]
- Z.H. Fong, T.W. Chiang, C.W. Tsay, Mathematical model for parametric tooth profile of spur gear using line of action, Math. Comput. Model. 36, 603–614 (2002) [CrossRef] [Google Scholar]
- S. Luo, Y. Wu, J. Wang, The generation principle and mathematical models of a novel cosine gear drive, Mech. Mach. Theory 43, 1543–1556 (2008) [CrossRef] [Google Scholar]
- G. Hlebanja, S-gears for wind power turbine operation conditions, Mach. Des. 4, 123–130 (2012) [Google Scholar]
- J. Wang, L. Hou, S. Luo, R.Y. Wu, Active design of tooth profiles using parabolic curve as the line of action, Mech. Mach. Theory 67, 47–63 (2013) [CrossRef] [Google Scholar]
- L. Liu, F. Meng, J. Ni, A novel non-involute gear designed based on control of relative curvature, Mech. Mach. Theory 140, 144–158 (2019) [CrossRef] [Google Scholar]
- Y. Wang, S. Ren, Y. Li, Design and manufacturing of a novel high contact ratio internal gear with a circular arc contact path, Int. J. Mech. Sci. 153–154, 143–153 (2019) [Google Scholar]
- I.R. Shabanov, On the gear transmission with a conchoidal path of contact, Nadyozhnost i Kachestvo Zubchatych Peredach 18-67-106, 1–8 (1967) (in Russian) [Google Scholar]
- V.P. Shishov, P.L. Nosko, O.A. Revyakina, Cylindrical transmissions with arch teeth, Publishing House of Volodymyr Dahl East Ukrainian National University, Lugansk, 2004 (in Russian) [Google Scholar]
- H.J. Watson, Modern Gear Production, Pergamon Press, Oxford (1970) [Google Scholar]
- V.P. Shishov, O.A. Revyakina, P.N. Tkach, On the character of teeth contact in cylindrical transmissions, Bull. Natl. Tech. Univ. 21, 110–119 (2007) (in Russian) [Google Scholar]
- H. Linke, J. Börner, R. Heß, Cylindrical Gears: Calculation, Materials, Manufacturing, Carl Hanser Verlag, Munich (2016) [CrossRef] [Google Scholar]
- Y.N. Drozdov, V.I. Smirnov, Study of the coefficient of sliding friction for high contact parameters, Vestnik Mashinostroeniya 6, 19–23 (1977) (in Russian) [Google Scholar]
- V. Onishchenko, Tooth wear modeling and prognostication parameters of engagement of spur gear power transmissions, Mech. Mach. Theory 43, 1639–1664 (2008) [CrossRef] [Google Scholar]
Cite this article as: P. Tkach, P. Nosko, O. Bashta, Y. Tsybrii, O. Nosko, High load capacity spur gears with conchoidal path of contact, Mechanics & Industry 22, 47 (2021)
All Tables
All Figures
 |
Fig. 1 Geometry of conchoidal gears: (a) generating surface; (b) pinion 1 and gear 2; (c) reference profile. |
| In the text | |
 |
Fig. 2 Geometry of the teeth active profiles of the pinion 1 and gear 2. |
| In the text | |
 |
Fig. 3 Ratio between contact strength coefficients θcon and θinv. |
| In the text | |
 |
Fig. 4 Ratio between energy efficiencies ηcon and ηinv. |
| In the text | |
 |
Fig. 5 Hob cutter tooth profile. |
| In the text | |
 |
Fig. 6 Gear test rig. |
| In the text | |
 |
Fig. 7 Gear test rig energy efficiency ηe vs pinion torque T1. |
| In the text | |
 |
Fig. 8 Gear box oil temperature ϑ vs pinion torque T1. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


