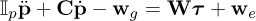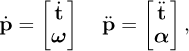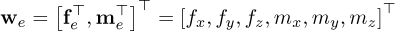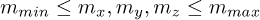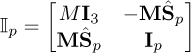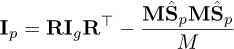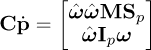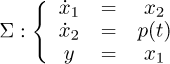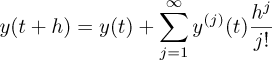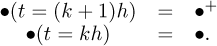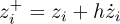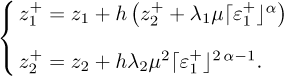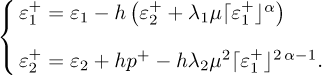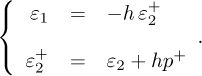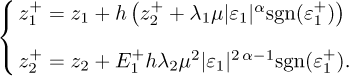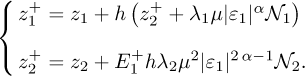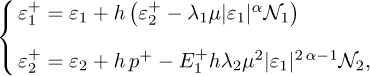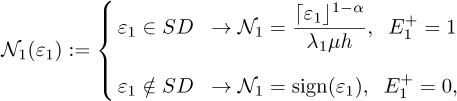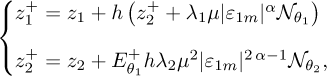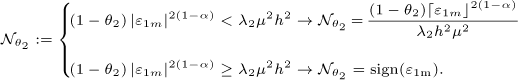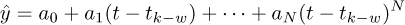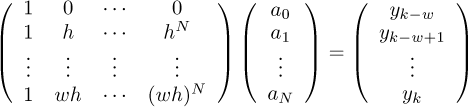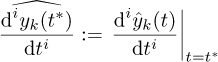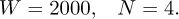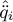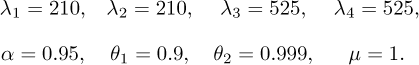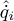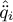| Issue |
Mechanics & Industry
Volume 25, 2024
High fidelity models for control and optimization
|
|
|---|---|---|
| Article Number | 11 | |
| Number of page(s) | 10 | |
| DOI | https://doi.org/10.1051/meca/2024005 | |
| Published online | 09 April 2024 | |
A semi-implicit homogeneous discretized differentiator based on two projectors: experimental validation on a cable-driven parallel robot
1
Nantes Université, École Centrale de Nantes, CNRS, LS2N,
UMR 6004,
F-44000
Nantes,
France
2
QUARTZ EA 7393, ENSEA,
Cergy-Pontoise,
France, France
* e-mail: yannick.aoustin@univ-nantes.fr
Received:
22
February
2023
Accepted:
24
January
2024
This work is dedicated to the application of a semi-implicit homogeneous differentiator to estimate the angular velocity and the angular acceleration of each of the eight electric motors of the CRAFT cable-driven parallel robot from the recording of the angular position of their respective output shaft. These motors drive the winding or unwinding of eight cables to move the robot moving-platform. The results show that this differentiator, whose the definition is respectively based on two projectors, is an extremely efficient tool for estimating the angular velocities and accelerations of the eight motors. These estimated velocities and accelerations are much less noisy than their reference signals obtained by backward difference. Moreover, the estimated quantities obtained with this differentiator are successfully compared to those obtained by a non-linear observer based on the interpolation and numerical difference of the measured position variable. Those promising results will definitely contribute to a better control of the CRAFT robot.
Key words: Cable-driven parallel robot / velocity estimation / acceleration estimation / homogeneous differentiators / homogeneous discretized differentiators / semi-implicit Euler discretization / projectors
© L. Michel et al., Published by EDP Sciences, 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
A cable-driven parallel robot (CDPR) consists of a moving-platform that is connected to a rigid frame by means of cables and actuators, the latter being generally mounted on the ground. Most of the existing robots are powered by electric motors. These robots are very attractive for handling tasks [1–3] because of their low inertia, a higher payload to weight ratio and a large workspace compared to conventional manipulator robots with articulated rigid limbs. A CDPR, named CRAFT and located at LS2N, Centrale Nantes campus, is equipped with eight actuators and a moving-platform. Each motor has an encoder sensor measuring the angular velocity of its output shaft allowing to evaluate the performances of the differentiation solutions. The moving-platform has six degrees of freedom. This moving platform is thus over-actuated [4].
The possible application fields of a CDPR can be industrial, or dedicated to search-and-rescue operations. However, for tasks such as motion planning realized with CDPRs, haptic control is still improvable. To deal with various restrictions on cable tensions, cable elasticity, collisions and obstacle avoidance, over-actuation of the moving platform is actually a challenging scientific problem [5], [6].
As a consequence the control of CDPRs is challenging. One key point for their control design is the access, for each electric motor shaft, to the angular variable and its time derivatives. These data are useful to design the robot control in tracking position or in haptic control [7]. Usually, the measurement of the angular variable of the output shaft of each actuator is made thanks to an encoder sensor or a resolver-to-digital converter. However, the measurement of the angular velocity of the output shaft is not usual. Due to weight restrictions, reliability, and financial cost, a tachymeter is not usually available.
A solution to get the value (or the estimation) of the angular velocity can be based on numerical differentiators, which are currently the focus of very active research. For CRAFT in order to estimate the angular velocity and angular acceleration from the measured output motor shaft angles the design of continuous time differentiators can be a good solution [8], [9]. However to be closer to physical systems, discretization differentiation is more convenient. The problem of digital differentiation is not new and several methods exist. Diop et al. [10] investigate interpolation and numerical differentiation for constructing an approach to the design of nonlinear observers. The measured signal is sampled at discrete instants and interpolated by a polynomial for a window data. This elegant method is unfortunately not applicable in real time without introducing delays depending on the computation windows. Realtime discrete signal differentiation has been investigated with sliding-modes techniques. Carjaval-Rubio et al. [11] derived two discretization algorithms for the homogeneous high-order sliding mode. The main problem to design digital differentiation is how to reject as much as possible the noise effects. Acary & Brogliato [12] introduced an implicit discretization technique, which overcomes some limitations such as the chattering of the classical sliding-mode. They replace the sign function by an implicit projector. Mojallizadeh et al. [13] develop the implicit discretization scheme for the arbitrary-order super-twisting differentiator. This very effective method has, however, a weakness in some areas, which will be explained in this paper. Semi-implicit discretization is an alternative method that overcomes the implementation difficulties of implicit discretization of homogeneous differentiators. The semi-implicit discretization of various differentiators has been studied and tested. The algorithms for realizing causal systems are provided and semi-implicit schemes are presented to make the implementation straightforward. On the other hand, for control purpose, Yang et al. [14] proposed a semi-implicit Euler algorithm for the multivariable super twisting algorithm (STA) in order to attenuate the numerical chattering and preserve its robustness during digital implementations. They analyzed the stability of the semi-implicit Euler implementation algorithm theoretically. Xiong et al. [15] developed a semi-implicit implementation scheme for the STA with a high control accuracy that is insensitive to the gain overestimation of the STA. A semi-implicit discretization differentiator with one projector was studied in [16] and applied for a nonlinear and non-stationary pneumatic setup [17]. In [18] Yang et al. presents a digital implementation scheme for the conditioned STA based on a semi-implicit Euler discretization method. Readers can refer to [19] to obtain a good survey with details and a state-of-the-art of differentiation solutions.
Among the numerous algorithms in the framework of the discrete homogeneous differentiation, the proposed differentiator SIHD-2, which combines explicit terms with implicit one including two projectors in order to reduce the effects of chattering as well as noise and disturbances, is efficient [20]. This method was chosen to estimate the velocity of the CRAFT actuators.
The contribution of this paper is to adapt this algorithm with its parameter in order to estimate both the angular velocity and angular acceleration of each motor shaft of CRAFT. Furthermore, the performance of the new numerical differentiation scheme is compared experimentally to the performance of the algorithm proposed by Diop et al. [10]. This comparison shows that the results of the differentiator are coherent with those of this algorithm for both angular velocity and angular acceleration.
The remaining of the paper is organized as follows. Section 2 is devoted to the presentation of CRAFT namely, its geometric, kinematic, and dynamic models. The problem is stated in Section 3 in order to present the homogeneous continuous-time differentiator. The semi-implicit Euler discretization is determined in Section 4. The experimental results are presented in Section 5. Conclusions and future work are drawn in Section 6.
 |
Fig. 1 CRAFT’s prototype located at LS2N, Nantes, France. |
2 The cable-driven parallel robot CRAFT
This section is dedicated to the description of CRAFT and its dynamic model.
2.1 CRAFT prototype located at LS2N, Nantes, France
The cable-driven parallel robot prototype, named CRAFT is located at LS2N, France. The base frame of CRAFT is 4 m long, 3.5 m wide, and 2.7 m high, see Figure 1. The three-DoF translational motions and the three-DoF rotational motions of its suspended moving-platform (MP) are controlled with eight cables being respectively wound around eight actuated reels fixed to the ground. The MP is 0.28 m long, 0.28 m wide, and 0.2 m high, its overall mass being equal to 5 kg.
Figure 2 shows the main hardware of the prototype, which consists of a PC (equipped with © MATLAB and © ControlDesk software), eight © PARKER SME60 motors and TPD–M drivers, a © dSPACE DS1007-based real-time controller and eight custom made winches. Each cable can exert a tension up to 150 N to the MP. The maximum velocity of each cable is equal to 5.9 m/s. The cable tensions are measured using eight FUTEK FSH04097 sensors, one for each cable, attached to cable float points. Their signal is amplified using eight FSH03863 voltage amplifiers and sent to the robot controller by a coaxial cable. Their measurement frequency is 1 kHz.
 |
Fig. 2 The hardware of the prototype CRAFT. |
2.2 Dynamic Model
The dynamic model of CRAFT used in this paper only considers the mass and inertia of the MP, the latter being pulled by the cables. Indeed, assuming that the diameters of the cables and the pulleys are small, the dynamic effects of the pulleys and the cables are neglected. A more general dynamic model taking into account also the dynamics of the motors, gearboxes, winches could be considered, but would not provide fundamentally different information on the movement of the platform.
As described in [2] the dynamic equilibrium equation of the moving platform is expressed as:
where W is the wrench matrix that maps the cable tension vector τ into the wrench exerted by the cables onto the MP, and
where  and
and  are the vectors of the moving platform linear velocity and acceleration, respectively, while ω =[ωx, ωy, ωz]⊤ and α = [αx, αy, αz]⊤ are the vectors of the moving platform angular velocity and acceleration, respectively.
are the vectors of the moving platform linear velocity and acceleration, respectively, while ω =[ωx, ωy, ωz]⊤ and α = [αx, αy, αz]⊤ are the vectors of the moving platform angular velocity and acceleration, respectively.
The external wrench we is a 6-dimensional vector expressed in the fixed reference frame 𝓕b and takes the form
ƒx, ƒy, and ƒz are the x, y, and z components of the external force vector fe. mx, my, and mz are the x, y, and z components of the external moment vector me, respectively. The components of the external wrench we are assumed to be bounded as follows
According to (4) and (5), the set [we]r, called the Required External Wrench Set (REWS), that the cables have to balance is a hyper-rectangle.
The Center of Mass (CoM) of the moving platform, G, may not coincide with the origin of the frame 𝓕p attached to the platform. The mass of the platform being denoted by M, the wrench w𝒢 due to the gravity acceleration vector g is defined as follows
where I3 is the 3 × 3 identity matrix, MSp = R [Mxp, Myp, Mzp]⊤ is the first momentum of the moving platform defined with respect to frame 𝓕b. The vector Sp = [xp, yp, zp]⊤ defines the position of G in frame 𝓕p. 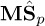 is the skew-symmetric matrix associated with MSp.
is the skew-symmetric matrix associated with MSp.
The matrix 𝕀p represents the spatial inertia of the platform
where Ip is the inertia tensor matrix of the moving-platform, which can be computed by the Huygens-Steiner theorem from the moving platform inertia tensor, I𝒢, defined with respect to the platform CoM
R is the rotation matrix defining the moving-platform orientation and C is the matrix of the centrifugal and Coriolis wrenches, defined as
where  is the skew-symmetric matrix associated to ω.
is the skew-symmetric matrix associated to ω.
The 3D dynamic model of CRAFT is non-linear. In order to perform the most successful positioning or co-manipulation task, the knowledge of the robot state is necessary. CRAFT is not equipped with a sensor to measure the velocity of the output motor shaft angles. A numerical derivative of output motor shaft angles is thus required. In the following, a strategy is presented in order to obtain the numerical derivation of the output motor shaft angles.
3 Statement of the problem
The purpose is to estimate the velocity of the angular variable exclusively from the measured position of the output shaft for each of the eight motors. The continuoustime and the Euler implicit state models of the considered system are presented. Then the homogeneous continuoustime differentiator is introduced and its semi-implicit discretization is finally justified.
3.1 Continuous-time state model systems
The continuous model under consideration is the following one:
where x1 and x2 are respectively the angular variable and its velocity; y is the measure signal of 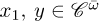 , i.e., y is assumed to be as an analytic signal:
, i.e., y is assumed to be as an analytic signal:
where y(j) denotes the jth time derivative of y and h is the sampling time.
Let p(t) be a bounded perturbation, which is unknown such that there exists:
Let the following notation be used for the discretized variable:
The perturbation p(t) is assumed to be a constant parameter or a slow variable. This implies that for a sufficient small sampling-time h > 0, p ≡ p+. As a consequence an implicit Euler discretization of the continuous-time model can be written with (13) as follows:
3.2 Homogeneous continuous-time differentiator
Homogeneity approach is very interesting because if for example a local stability is obtained due to the dilatation, this framework allows extending this local property to global settings, [21]. The option of a continuous-time homogeneous differentiator is therefore chosen under the assumption (12) [22], [23]. This differentiator can be written as,
where α ∊ [0.5 , 1[ has to be fixed [24], ɛ1 = y − z1, and the notation[•]α = |•|α sgn(•) is adopted along the paper. If α = 0.5 the algorithm (15) becomes the super-twisting differentiator [8] that has a very good accuracy with respect to perturbation, but it is more sensitive to noise. If α = 1 the algorithm (15) becomes a linear differentiator that has good properties with respect to noise but its accuracy is degraded under perturbation [23]. The degree of homogeneity of the differentiator (15) d is equal to α — 1 with respect to dilatation Λr with r = (r1 = 1, r2 = 1) [22]. Moreover, λi > 0, i = 1, 2 are the linear part gains, which are considered and allow to have the eigenvalues of the differentiation error ɛ1 in the left part of the complex plane, i.e., the eigenvalues have a negative real part, while the coefficient µ is chosen sufficiently large to cancel the effect of the unknown perturbation p(t).
In order to be closer to the cable-driven parallel robot CRAFT and deal with real signal differentiation application, differentiators based on an Euler discretization approach will be designed in the next section.
3.3 Existing Euler discretization of the homogeneous continuous-time differentiator (15)
To design the Euler discretization of the continuous-time homogeneous differentiator (15), several feasible solutions are obtained using explicit, implicit or semi-implicit methods. The semi-implicit method is chosen in this paper for the following reasons.
Among the different Euler discretization methods two can be considered as follows:
• The usual explicit method: zi and 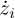 for i = 1, 2 are known at tk = kh and
for i = 1, 2 are known at tk = kh and 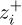 is calculated such as.
is calculated such as.
With (16) the explicit Euler discretization of the continuous-time differentiator (15) is deduced as follows,
This algorithm (17) unfortunately leads to a chattering effect and therefore the numerical solution is not attractive.
• Implicit method: zi is known,  is chosen such that
is chosen such that 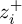 is equal to.
is equal to.
With (18) the implicit Euler discretization [12] of the continuous-time differentiator (14) is deduced as follows,
Subtracting the two equations of (19) from the first two equations of (14) gives:
with ɛi = xi − zi (i = 1, 2). As it is usually assumed with the implicit Euler method [25], an analyze of the dynamics on the sliding surface  leads to the following estimation error model:
leads to the following estimation error model:
The scalar equations of (21) are similar and the feedback correction terms as function of λi (i = 1, 2) are removed. There is no possible correction term to reject the influence of the perturbation term p+ in this error model (21). If the perturbation term p+ is zero in the second scalar equation of (21), the variable ɛ2 is steady stable and equals to a constant. However, the second scalar equation of (21) could have an unstable dynamics when the perturbation term p+ is non-zero.
A third approach, the semi-implicit homogeneous Euler discretization allows to overcome the drawbacks of these two previous numerical schemes, [16]. The implicit discretization is kept only in the signum multi valued function 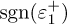 while all other terms are explicitly discretized as follows.
while all other terms are explicitly discretized as follows.
That is why this approach is chosen to discretize the continuous-time model (15). This is presented in the next section to design a variant of the semi-implicit homogeneous Euler differentiator, where  is computed to cancel the influence of the past in
is computed to cancel the influence of the past in 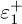 dynamic
dynamic 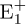 is the convergence flag of
is the convergence flag of 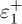 .
.
4 Semi-implicit Homogeneous Euler differentiator based on two projectors (SIHD-2)
The considered semi-implicit Euler discretization differentiator is defined with the acronym SIHD-2 because two rojectors 𝒩1 and 𝒩2 are used to design its correction terms [20]. The strategy aims to “generalize” the multi valued sign function sgn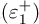 in sliding-based differentiator in order to reduce the chattering and preserve stability properties for high time steps. The two different projectors, 𝒩1 and 𝒩2 are respectively dedicated to the estimation of z1 and z2. From the experimental setup CRAFT it has been highlighted that the SIHD-2 algorithm offers better performances than with only one projector. As a result, the semi-implicit homogeneous Euler discretization based on two projectors (SIHD-2) reads as:
in sliding-based differentiator in order to reduce the chattering and preserve stability properties for high time steps. The two different projectors, 𝒩1 and 𝒩2 are respectively dedicated to the estimation of z1 and z2. From the experimental setup CRAFT it has been highlighted that the SIHD-2 algorithm offers better performances than with only one projector. As a result, the semi-implicit homogeneous Euler discretization based on two projectors (SIHD-2) reads as:
Subtracting the two equations of (23) from the first two of (14) leads to the following estimation error model:
Here the definition of the projector 𝒩1 and the tuning of the flag 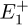 are such as:
are such as:
with the domain of attraction 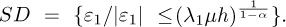 .
.
When ɛ1 ∊ SD the equality ɛ1 = h ɛ2 (remark that this equality is different from the one of (21)) holds, 𝒩2 reads as:
where 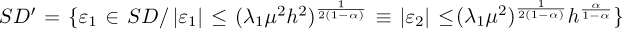 . The terms |e1|α and |e1|2α−1 are the explicit parts while the projectors (the terms 𝒩1 and 𝒩2) refer to the implicit part.
. The terms |e1|α and |e1|2α−1 are the explicit parts while the projectors (the terms 𝒩1 and 𝒩2) refer to the implicit part.
5 Experimental validation
5.1 Condition of data capture
For each of the eight electrical motors an encoder sensor measures the angular variable qi, (i = 1, ⋯, 8) of its shaft. The eight motors are equipped with a gearbox reducer of ratio n = 8. The measured value is divided by n in order to obtain the angular position of the output shaft of the gearbox reducer. The robot CRAFT has no tachometer. As a result, there is no reference measurement of angular velocity and hence angular acceleration for each of the eight motors. The reference signals of the rotation velocity and the rotation acceleration are obtained thanks to the algorithm proposed by Diop et al. [10] and recalled in this section. As this algorithm cannot be used in real time, the comparison with the differentiator SIHD-2 algorithm is made offline. This choice was made because it is well-known robust with respect to measurement noise, which is not the case with conventional methods such as numerical differentiation (see Fig. 6). The sampling period of the acquisition data from the experimental setup is equal to h = 1 ms. Of course, it’s possible to apply the estimator algorithm proposed by Diop et al. in real time, i.e., online by its definition on a moving segmentation window. However, applying this estimator algorithm in real time will cause the estimated angular velocity and acceleration to lag behind the actual angular velocity and acceleration.
5.2 Attenuation noise projectors
The measured angular positions are noisy such as y becomes ym = x1 + η where η is a measurement noise. The output corrective term ɛ1 becomes ɛ1m = ym − z1. As a consequence, a modified projector including a new parameter θ is introduced in order to mitigate the influence of noise. The semi-implicit Euler homogeneous differentiator SIHD 2 becomes:
SIHD-2
with
and
5.3 Principle of the observer strategy proposed by Diop et al. [10]
For a window of the recorded data  an interpolating polynomial function of order N is denoted by
an interpolating polynomial function of order N is denoted by
where tk = kh and w is such that wh defines the length in time of the moving window used for data interpolation and w + 1 in the number of data points in the window.
The coefficients {a0, a1, ⋯, aN} are determined from the squares solution of the following over-determined system:
with respect to the Euclidean norm. The estimates of the ith time derivatives of y at time t* are determined by
For the experimental tests of this current study the parameters of this numerical differentiation are:
 |
Fig. 3 Estimation variables |
5.4 Determination of the semi-implicit Homogeneous Euler differentiator parameters
The estimation of the angular velocity 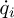 and the angular acceleration
and the angular acceleration 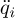 with the SIHD-2 algorithm is carried out by connecting in cascade two SIHD-2 differentiators, which are similar to (27), see Figure 3. Eight parameters are defined for the SIHD-2 algorithm in : λ1 , λ2, θ1 for the differentiator 1, λ3, λ4, and θ2 for the differentiator 2, α, and µ for both. The λi, i = 1, 4 parameters are chosen such that the linear part is stable. The value of homogeneous exponent α is chosen between the coefficient of Levant’s differentiator (α* = 0. 5) and the linear solution of the dis-cretized differentiator SIHD-2 (α* = 1). The parameters θj, j = 1, 2 is chosen by numerical trial an error allowing a good filtering of the noise, i.e., 0.5 < θj < 1. The µ parameter is also chosen by numerical test trial and error to determine the best possible action of the projectors 𝒩θ1
with the SIHD-2 algorithm is carried out by connecting in cascade two SIHD-2 differentiators, which are similar to (27), see Figure 3. Eight parameters are defined for the SIHD-2 algorithm in : λ1 , λ2, θ1 for the differentiator 1, λ3, λ4, and θ2 for the differentiator 2, α, and µ for both. The λi, i = 1, 4 parameters are chosen such that the linear part is stable. The value of homogeneous exponent α is chosen between the coefficient of Levant’s differentiator (α* = 0. 5) and the linear solution of the dis-cretized differentiator SIHD-2 (α* = 1). The parameters θj, j = 1, 2 is chosen by numerical trial an error allowing a good filtering of the noise, i.e., 0.5 < θj < 1. The µ parameter is also chosen by numerical test trial and error to determine the best possible action of the projectors 𝒩θ1
and  . The numerical values of these eight parameters are tuned as follows:
. The numerical values of these eight parameters are tuned as follows:
 |
Fig. 4 Experimental data for the first four motors: Recording angular positions qi (radian), estimated angular velocities |
5.5 Discussion about the experimental results
Figures 4 and 5, present for the eight motors the recorded angular positions of the output shaft, which supports the winch, after the gearbox, and the associate velocities and associate accelerations calculated with the SIHD-2 algorithm. The behavior of the differentiator is quasi uniform whatever the motors. When the platform stops no significant delay can be identified with the velocity and acceleration signals. As there is no tachymeter sensor on the motor shaft, it is difficult to present the backward difference as the one that gives the reference angular velocity and acceleration. Nevertheless, we can evaluate each of the angular velocity signal in terms of their sensitivity to noise. In a common time window, which is equal to 29s-31s and represented by a black dashed line in Figure 6 the standard deviation is determined for the angular velocity  and the angular acceleration
and the angular acceleration 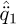 respectively estimated with the SIHD-2 method. Remark that the velocity discontinuity at 60 s induces an overshoot with the algorithm, which is proposed by Diop et. al. It is due to the fact that the polynomial function before 60 s is different from the one after, a constant. With respect to the same phenomenon, SIHD-2 is destabilized at 60 s and converges after a couple of seconds. Table 1 gathers the results for the fourth motor, which represents quite well the general behavior of the eight motors. The sensitivity to noise is much lower for the angular velocity and acceleration signals with the SIHD-2 method than with the backward difference. Figure 6 proves that the results obtained with the differentiator are consistent with those obtained by interpolating the measured positions and the numerical differences of the designed polynomial functions. Although the angular position graph may give the impression of a continuous signal, it is nonetheless a measured signal sampled at the 10 ms period. When digitally derived with the Backward difference method, i.e., the simplest Euler differentiation (function of Matlab diff®), we can observe noise, see Figure 7.
respectively estimated with the SIHD-2 method. Remark that the velocity discontinuity at 60 s induces an overshoot with the algorithm, which is proposed by Diop et. al. It is due to the fact that the polynomial function before 60 s is different from the one after, a constant. With respect to the same phenomenon, SIHD-2 is destabilized at 60 s and converges after a couple of seconds. Table 1 gathers the results for the fourth motor, which represents quite well the general behavior of the eight motors. The sensitivity to noise is much lower for the angular velocity and acceleration signals with the SIHD-2 method than with the backward difference. Figure 6 proves that the results obtained with the differentiator are consistent with those obtained by interpolating the measured positions and the numerical differences of the designed polynomial functions. Although the angular position graph may give the impression of a continuous signal, it is nonetheless a measured signal sampled at the 10 ms period. When digitally derived with the Backward difference method, i.e., the simplest Euler differentiation (function of Matlab diff®), we can observe noise, see Figure 7.
 |
Fig. 5 Experimental data for the last four motors: Recording angular positions qi (radian), estimated angular velocities |
 |
Fig. 6 Experimental data for the fourth motor: (top) Recording angular positions defined by (q1); estimated angular position defined by |
 |
Fig. 7 Recording angular positions q1 (radian), estimated angular velocities |
Standard deviation to evaluate the noise for the angular velocity and the angular acceleration of the fourth motor (BD means Backward difference method).
6 Conclusion
The cable-driven parallel robot CRAFT is a complex mechanical system for which the control is difficult due to its over-actuated nature and cable tension constraints. However, its future is promising for applications such as handling, rescue or personal assistance. Two new semi-implicit homogeneous differentiators are applied with success to estimate the angular velocity of the output shaft of the eight motors of the robot CRAFT. The obtained velocities are less noisy than those calculated with backward difference.
The results open a great perspective window for this family of robots. First the application of semi-implicit homogeneous differentiators for identification tasks of model parameters such as Coulomb or kinematic frictions, inertia moments, masses could be very efficient. Secondly one important task of a cable-driven parallel robot is the co-manipulation between its effector and human thanks a force sensor. From the measure of a force sensor, a mass parameter allows to deduce an acceleration vector. After a double integration of this acceleration vector a Cartesian trajectory is deduced. Finally, a reference trajectory for each motor can be deduced thanks an inverse geometric model and an inverse kinematic model [7]. The tracking of these reference trajectories has to be perfect with high gain values, from which denoising signals are requested, to obtain an efficient co-manipulation. As a consequence the semi-implicit homogeneous differentiator SIHD-2 will be very useful for the cable-driven parallel robot CRAFT.
Funding
This work was supported by the ANR project DigitSlid ANR-18-CE40-0008-01 (https://anr.fr/Project-ANR-18-CE40-0008) and the ANR CRAFT project, grant ANR-18-CE10-0004 (https://anr.fr/Project-ANR-18-CE10-0004). This work has been partially supported by ROBOTEX 2.0 (Grants ROBOTEX ANR-10-EQPX-44-01 and TIRREX ANR-21-ESRE-0015).
Conflicts of Interest
The authors have nothing to disclose.
Data Availability Statement
This article has no associated data generated and/or analyzed.
Author Contribution Statement
Conceptualization: Yannick Aoustin, Loic Michel and Jean-Pierre Bar-bot; Methodology, Conceptualization: Yannick Aoustin, Loic Michel, Malek Ghanes, Franck Plestan and Jean-Pierre Barbot; Software: Loic Michel; Validation: Loic Michel, Stéphane Caro and Marceau Metillon; Formal Analysis: Yannick Aoustin, Loic Michel, Jean-Pierre Barbot, Malek Ghanes, Franck Plestan; Investigation: Yannick Aoustin, Loic Michel, Jean-Pierre Barbot; Resources: Loic Michel, Stéphane Caro and Marceau Metillon; Data Curation: Loic Michel, Stéphane Caro and Marceau Metillon; Writing – Original Draft Preparation: Yannick Aoustin, Loic Michel, Jean-Pierre Barbot; Writing – Review & Editing: Yannick Aoustin, Loic Michel, Jean-Pierre Barbot; Visualization: Yannick Aoustin, Loic Michel, Malek Ghanes, Franck Plestan, Marceau Metillon, Stéphane Caro and Jean-Pierre Barbot; Project Administration: Franck Plestan; Funding Acquisition: Franck Plestan.
References
- E. Picard, S. Caro, F. Plestan, F. Claveau, Control solution for a cable-driven parallel robot with highly variable payload, Vol. 5B: 42nd Mechanisms and Robotics Conference of International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, 2018, p. V05BT07A013 [Google Scholar]
- L. Gagliardini, M. Gouttefarde, S. Caro, Determination of a dynamic feasible workspace for cable-driven parallel robots, Proceedings in Advanced Robotics, Springer, 2016, pp. 361–370 [Google Scholar]
- H. Tan, L. Nurahmi, B. Pramujati, S. Caro, On the reconfiguration of cable-driven parallel robots with multiple mobile cranes, in: 2020 5th International Conference on Robotics and Automation Engineering (ICRAE), 2020, pp. 126–130 [CrossRef] [Google Scholar]
- U.A. Mishra, M. Metillon, S. Caro, Kinematic stability based afg-rrt path planning for cable-driven parallel robots, in: 2021 IEEE International Conference on Robotics and Automation (ICRA), 2021, pp. 6963–6969 [CrossRef] [Google Scholar]
- M. Gouttefarde, J.-F. Collard, N. Riehl, C. Baradat, Geometry selection of a redundantly actuated cable-suspended parallel robot, IEEE Trans. Robotics 31, 501–510 (2015) [CrossRef] [Google Scholar]
- H. Hussein, J.C. Santos, J.-B. Izard, M. Gouttefarde, Smallest maximum cable tension determination for cable-driven parallel robots, IEEE Trans. Robotics 37, 1186–1205 (2021) [CrossRef] [Google Scholar]
- P. Lemoine, P.P. Robet, M. Gautier, C. Damien, Y. Aoustin, Haptic control of the parallel robot orthoglide, in: 2019 in Proceedings of the 24nd Congrès Français de Mécanique, CFM, Brest, France, 26–30 August, 2019 [Google Scholar]
- A. Levant, Robust exact differentiation via sliding mode technique, Automatica 34, 379–384 (1998) [CrossRef] [MathSciNet] [Google Scholar]
- A. Levant, Sliding order and sliding accuracy in sliding mode control, Int. J. Control 58, 1247–1263 (1993) [CrossRef] [Google Scholar]
- S. Diop, J. Grizzle, P. Moraal, A. Stefanopoulou, Interpolation and numerical differentiation for observer design, in: Proceedings of 1994 American Control Conference – ACC ’94, Vol. 2, 1994, pp. 1329–1333 [Google Scholar]
- J.E. Carvajal-Rubio, A.G. Loukianov, J.D. Sanchez-Torres, M. Defoort, On the discretization of a class of homogeneous differentiators, in: 2019 16th International Conference on Electrical Engineering, Computing Science and Automatic Control (CCE), 2019, pp. 1–6 [Google Scholar]
- V. Acary, B. Brogliato, Y.V. Orlov, Chattering-free digital sliding-mode control with state observer and disturbance rejection, IEEE Trans. Automatic Control 57, 1087–1101 (2012) [CrossRef] [MathSciNet] [Google Scholar]
- M.M. Rasool, B. Brogliato, V. Acary, Time-discretizations ofdiffer-entiators: design of implicit algorithms and comparative analysis, Int. J. Robust Nonlinear Control 31 (2021) [MathSciNet] [Google Scholar]
- X. Yang, X. Xiong, Z. Zou, Y. Lou, S. Kamal, J. Li, Discrete-time multivariable super-twisting algorithm with semi-implicit Euler method, IEEE Trans. Circuits Syst. II: Express Briefs 69, 4443–4447 (2022) [Google Scholar]
- X. Xiong, G. Chen, Y. Lou, R. Huang, S. Kamal, Discrete-time implementation of super-twisting control with semi-implicit Euler method, IEEE Trans. Circuits Syst. II: Express Briefs 69, 99–103 (2022) [Google Scholar]
- L. Michel, M. Ghanes, F. Plestan, Y. Aoustin, J.-P. Barbot, Semi-implicit Euler discretization for homogeneous observer-based control: one dimensional case, IFAC-PapersOnLine 53, 5135–5140 (2020) [CrossRef] [Google Scholar]
- L. Michel, S. Selvarajan, M. Ghanes, F. Plestan, Y. Aoustin, J.P. Barbot, An experimental investigation of discretized homogeneous differentiators: pneumatic actuator case, IEEE J. Emerg. Selected Top. Ind. Electron. 2, 227–236 (2021) [CrossRef] [Google Scholar]
- X. Yang, X. Xiong, Z. Zou, Y. Lou, Semi-implicit Euler digital implementation of conditioned super-twisting algorithm with actuation saturation, IEEE Trans. Ind. Electron. 70, 8388–8397 (2023) [CrossRef] [Google Scholar]
- M.R. Mojallizadeh, B. Brogliato, A. Polyakov, S. Selvarajan, L. Michel, F. Plestan, M. Ghanes, J.-P. Barbot, Y. Aoustin, A survey on the discrete-time differentiators in closed-loop control systems: experiments on an electro-pneumatic system, Control Eng. Pract. 136, 105546 (2023) [CrossRef] [Google Scholar]
- L. Michel, M. Ghanes, F. Plestan, Y. Aoustin, J.-P. Barbot, Semi-implicit homogeneous Euler differentiator for a second-order system: validation on real data, in: 2021 60th IEEE Conference on Decision and Control (CDC), 2021, pp. 5911–5917 [CrossRef] [Google Scholar]
- L. Rosier, Homogeneous Lyapunov function for homogeneous continuous vector field, Syst. Control Lett. 19, 467–473 (1992) [CrossRef] [Google Scholar]
- W. Perruquetti, T. Floquet, E. Moulay, Finite-time observers: application to secure communication, IEEE Trans. Automatic Control 53, 356–360 (2008) [CrossRef] [MathSciNet] [Google Scholar]
- M. Ghanes, J.-P. Barbot, L. Fridman, A. Levant, R. Boisliveau, A new varying-gain-exponent-based differentiator/observer: an efficient balance between linear and sliding-mode algorithms, IEEE Trans. Automatic Control 65, 5407–5414 (2020) [CrossRef] [MathSciNet] [Google Scholar]
- Y. Hong, J. Huang, Y. Xu, On an output feedback finite-time stabilization problem, IEEE Trans. Automatic Control 46, 305–309 (2001) [CrossRef] [MathSciNet] [Google Scholar]
- V. Acary, B. Brogliato, Implicit Euler numerical scheme and chattering-free implementation of sliding mode systems, Syst. Control Lett. 59, 284–293 (2010) [CrossRef] [Google Scholar]
Cite this article as: L. Michel, M. Métillon, S. Caro, M. Ghanes, F. Plestan, J. P. Barbot, Y. Aoustin, A semi-implicit homogeneous discretized differentiator based on two projectors: experimental validation on a cable-driven parallel robot, Mechanics & Industry 25 11 (2024)
All Tables
Standard deviation to evaluate the noise for the angular velocity and the angular acceleration of the fourth motor (BD means Backward difference method).
All Figures
 |
Fig. 1 CRAFT’s prototype located at LS2N, Nantes, France. |
| In the text | |
 |
Fig. 2 The hardware of the prototype CRAFT. |
| In the text | |
 |
Fig. 3 Estimation variables |
| In the text | |
 |
Fig. 4 Experimental data for the first four motors: Recording angular positions qi (radian), estimated angular velocities |
| In the text | |
 |
Fig. 5 Experimental data for the last four motors: Recording angular positions qi (radian), estimated angular velocities |
| In the text | |
 |
Fig. 6 Experimental data for the fourth motor: (top) Recording angular positions defined by (q1); estimated angular position defined by |
| In the text | |
 |
Fig. 7 Recording angular positions q1 (radian), estimated angular velocities |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.