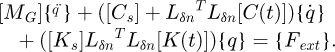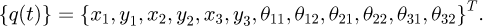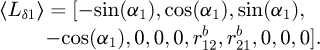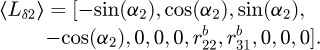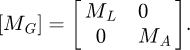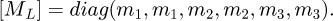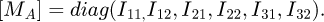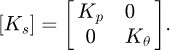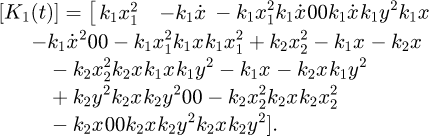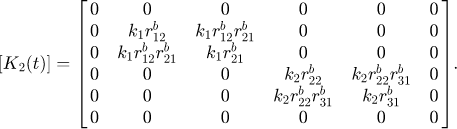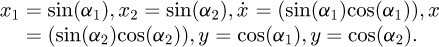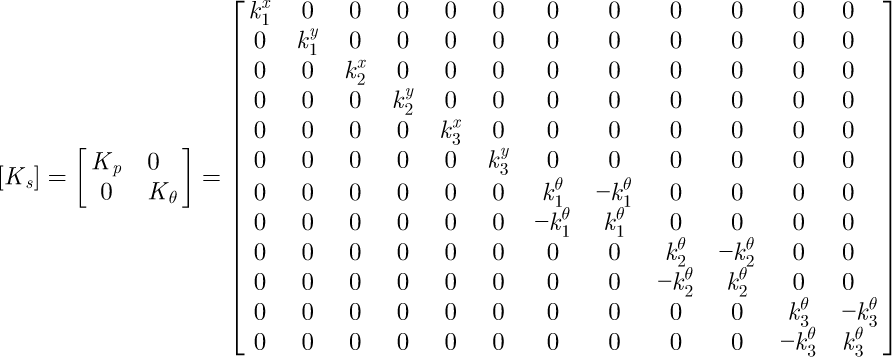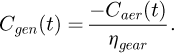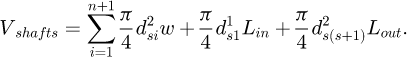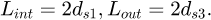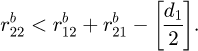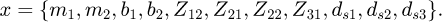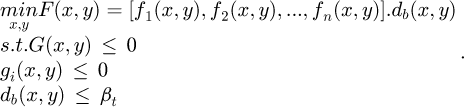| Issue |
Mechanics & Industry
Volume 25, 2024
|
|
|---|---|---|
| Article Number | 16 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/meca/2024010 | |
| Published online | 06 May 2024 | |
Original Article
Reliability based design optimization of a two-stage wind turbine gearbox
1
National Engineering School of Gabes, University of Gabes, Gabes, Tunisia
2
Normandie University, UNIHAVRE, CNRS, LOMC, 76600 Le Havre, France
3
Laboratory of Mechanics, Modeling and Production (LA2MP), National Engineering School of Sfax, University of Sfax, Sfax, Tunisia
4
Laboratory of Mechanics of Normandy (LMN), INSA Rouen Normandy, University of Rouen, St Etienne de Rouvray 76801, France
5
DRIVE Lab, University of Burgundy, Nevers, France
* e-mail: bilel.karmi@etu.univ-lehavre.fr
Received:
26
September
2023
Accepted:
8
March
2024
This paper describes a multi-objective reliability-based design optimization (MORBDO) of a two-stage wind turbine gearbox. The optimization process incorporates the gear's reliability of accounting for the uncertainty of its internal geometric parameters. It also ensures that constraints relating to the gear's reliability index and efficiency are respected. The objective functions are to minimize both the total volume and the center distance. A specific reliability target is established, and to address the multi-objective reliability-based design optimization (MORBDO), the hybrid method (HM) in conjunction with the constrained non-dominated sorting genetic algorithm (C-NSGA-II) is employed. The outcomes demonstrate that applying C-NSGA-II to solve the multi-objective reliability-based design optimization problem yields dependable Pareto solutions that are well-distributed in relation to the desired reliability level. The optimization using C-NSGA-II with a population size of 300 particles and 1000 generations produced the most favorable outcomes. This research significantly contributes to the multi-objective design optimization of wind turbine gear while simultaneously considering their reliability.
Key words: Gear system / multi-objective reliability optimization / Pareto front / NSGA-II / C-NSGA-II / hybrid method
© B. Karmi et al., Published by EDP Sciences 2024
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Gears are an essential component of many power transmission systems. They are essential for converting rotary motion and transmitting torque. They are widely used in a variety of industries, including automotive, aerospace, power generation and industrial robotics. Gear optimization is an active area of scientific research, aimed at improving their performance characteristics, including efficiency, durability, and noise reduction. In recent years, significant progress has been made in this field, thanks to technological advances, advanced modeling methods and numerical analysis techniques. Researchers and engineers have developed advanced tools to evaluate and optimize gear performance, considering factors such as load constraints, fatigue resistance, energy efficiency and weight constraints. In wind turbine, gearbox failure is responsible for approximately 95% of total downtime, leading to significant operational disruptions and incurring substantial repair costs. Hence, the main challenge is to limit gearbox failure rates and reduce weight, without affecting load capacity. The aim is to minimize the total volume of the gearbox, while maintaining its robustness and performance. The optimization has already been applied to multiple gear types such as helical gearing, spur gearing, bevel gearing, spiral gearing, and worm gearing by numerous researchers. In a study conducted by [1], the Non-Dominated Sorting Genetic Algorithm (NSGA-II) was employed for optimizing the total volume and total power loss of three different gear profiles: unmodified profile, smooth meshing profile, and high load capacity profile [2]. Similarly, Edmund and Arora [3] investigated the simultaneous optimization of three objective functions volume, power output, and center distance for a two-stage gear using the NSGA-II evolutionary algorithm. Chong et al. [4] explored the multi-objective optimal design of a cylindrical pair gears aimed at reducing geometric volume and meshing vibrations, applying an objective-based programming approach. Abuid and Ameen [5] applied a min-max combined with a single-variable search method to optimize a two-stage spur gear train, considering gear volume, center distance as well as the shaft dynamic factors as objective functions. Deb [6] employed NSGA-II to perform a multi-objective optimization of a gearbox with multiple stages. In their study, Zhong et al. [7] focused on the multi-objective optimization of a three-stage gear train using interactive physical programming. The objectives of the design included minimizing volume and maximizing surface fatigue strength and load capacity. Gologlu and Zeyveli [8] implemented the genetic algorithm in the volume optimization of a two-stage helical gear train. They inserted static and dynamic reintegration functions into the objective function to take account of design requirements such as frictional stress, bending strength, number of teeth on the gear and pinion, modulus and gear face width. Mendi et al. [9] introduced a multi-objective optimization approach based on the genetic algorithm for selecting an optimal design. Their objective was to minimize gear volume, shaft diameter, and bearing dimensions, while considering constraints at the tooth level. Marjanovic et al. [10] has developed an approach for spur gears that defines the optimum gear ratio, the optimum position of the shaft axis as well as the material required for optimal design. Golabi et al. [11] investigated the optimization of a gearbox by minimizing its total volume using the MATLAB optimization tool. They manipulated several parameters such as input power, transmission ratio and gear material hardness. Based on the optimization results, they estimated parameters such as number of stages, gear face widths and shaft diameters using the graphs obtained. Savsani et al and Panda et al. [12] studied the same optimization problem, which is based on an improved differential evolutionary (DE) algorithm. The objective of this optimization was to minimize the total mass of a single-stage spur gear, while satisfying ten non-linear constraints that involve design variables combined with integers.
In a recent study by [13] a novel multi-objective optimization approach was proposed for a planetary gearbox using a discrete version of the genetic algorithm known as NSGA-II. The objective functions aimed to minimize the weight and total power loss of the planetary gearbox. The design variables considered in the optimization included the number of teeth in the sun, planet, and ring gears, modulus, face width, input shaft diameter, and planet axis diameter. Qi et al. [14] introduced an optimization approach based on the Peak Sound Pressure Level to mitigate the radiated noise of the gearbox. Similarly, Lei et al. [15] have proposed a multi-objective optimization algorithm designed to reduce the causes of noise, including the value of the transmission error, its frequency and the maximum tooth load. To do this, a multi-objective optimization algorithm for optimizing gear micro geometry is used. However, it is worth noting that none of these authors explored optimization based on gear reliability. Reliability-Based Design Optimization (RBDO) has been developed to take account of design uncertainties. The main objective of the RBDO is to obtain a reliable optimal design by ensuring that the probability of failure remains below a predefined target level. To meet this challenge, several approaches have been proposed to address the problem of reliability optimization. Dammak et al. [16] examined the reliability of the optimal design of a brake disc through the use of a Kriging model. Barakat et al. [17] has adopted a global multi-objective reliability-based design optimization (MORBDO) approach for reinforced concrete beams with pre-tensioning. Zhang et al. [18] evaluated the resilience optimization of a tapered foam structure in which the RBDO method was applied. Lopez et al. [19] introduces an approach for conducting a global optimization in the context of reliability-based design (RBDO) for truss structures, focusing on both size and shape considerations. Braydi et al. [20] introduces the assessment of reliability and resilience for a nonlinear energy sink device concept. The research examines the system's performance and seeks optimal in both deterministic and probabilistic scenarios. Additionally, it explores the impact of different types of uncertainty modeling through various formulations of reliability-based robust design optimization. Zhou et al. [21] presented a theory based on the hybrid analysis of reliability and optimization to assess the uncertainty associated with limited objective information or subjective expert opinions. Eckert et al [22] focused on improving the traditional design of vehicle powertrains. To do so, they used a multi-objective optimization approach for the design of vehicle internal combustion engine (ICEV) transmissions and gear shifting control, aiming to minimize fuel consumption, exhaust emissions, and gearbox, power losses. Stefanović-Marinović et al. [23] presented a study on two-carrier planetary gear trains with complex configurations, featuring four external and two coupled shafts. The paper explores structural designs and investigates gear trains using coupled external shafts with controlling brakes for torque input and output. The paper also highlights extreme transmission ratio changes and establishes relationships between ideal torque ratios and required transmission ratios. This facilitates the selection of compound gear train designs. The conclusion presents optimal design parameters and the selected transmission solution based on input data.
Compared to the previously mentioned researches, this article makes a significant and new contribution by introducing a reliability-based optimization approach for the design of a two-stage wind turbine spur gear. The main novelty of this research lies in achieving an optimal combination of internal component dimensions for a two-stage wind turbine spur gear, considering the geometric uncertainties of its components. The objective is to enhance the gear's performance characteristics by addressing the geometric uncertainty and identifying the most efficient combination of dimensions. The used method is applied to develop an optimized and reliable model that guarantees a level of failure probability not exceeding a certain threshold. This comprehensive approach ensures a more robust and efficient design, enhancing the overall functionality and durability of the gear system in wind turbines. To achieve this, the Constrained Non-Dominated Sorting Genetic Algorithm (C-NSGA-II) will be employed. This algorithm will effectively address the multi-objective optimization problem by generating a set of Pareto solutions that are well-distributed.
2 Materials and methods
This section is divided into two main parts. The first part introduces the global dynamic model of the studied system, describes the geometry of the two-stage gearbox. In the following part, the optimization problem is reformulated by defining the objective functions, the design constraints, the design variables, and by describing the modeling approach used for reliability-based design optimization.
2.1 Studied system
2.1.1 Global dynamic model
The dynamic model consists of three blocks (j =1.3) each supported by a flexible bearing. Specifically, for the first block, the bending stiffness bearing is denoted as  , and the traction compression stiffness is denoted
, and the traction compression stiffness is denoted  . Similarly, for the second block, we have
. Similarly, for the second block, we have 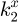 and
and 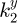 . Then,
. Then, 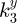 and
and 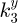 for the third block. The three shafts exhibit torsional stiffness, represented by
for the third block. The three shafts exhibit torsional stiffness, represented by 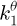 ,
, 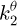 and
and  . It is assumed that the intermediate flexible shafts have negligible mass compared to the gearbox. The angular displacements of each wheel are denoted respectively as θ(1,1), θ(1,2), θ(2,1) ,θ(2,2), θ(3,1) and θ(3,2). Additionally, the linear displacements of the bearings in the plane orthogonal to the wheel's axis of rotation are measured as x1 and y1 for the first block, x2 and y2 for the second block, x3 and y3 for third block.
. It is assumed that the intermediate flexible shafts have negligible mass compared to the gearbox. The angular displacements of each wheel are denoted respectively as θ(1,1), θ(1,2), θ(2,1) ,θ(2,2), θ(3,1) and θ(3,2). Additionally, the linear displacements of the bearings in the plane orthogonal to the wheel's axis of rotation are measured as x1 and y1 for the first block, x2 and y2 for the second block, x3 and y3 for third block.
The dynamics of our system (Fig. 1) is described by the equation of motion derived using the Lagrange formulation. This equation is expressed in the standard matrix form as follows:
where:
⟨Lδn⟩ is a function of the n-level.
where 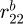 . and
. and 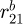 . represent respectively the basic radius of the pinion (1,2) and the gear (2,1).
. represent respectively the basic radius of the pinion (1,2) and the gear (2,1).
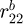 . and
. and 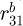 . represent respectively the basic radius of the pinion (2,2) and the gear (3,1).
. represent respectively the basic radius of the pinion (2,2) and the gear (3,1).
α1 and α2 are respectively the pressure angle for the first and the second gear stage.
The global mass matrix of the system, donated as [MG] is expressed as follows:
With [ML] is the matrix mass of the wheel and it is defined as [24]:
Where mj is the mass of the bloc j.
[MA] is the matrix of inertia and is written as follows [24]:
where Iij is the polar inertia of the Wheel (ji) relative to the axis of rotation.
The stiffness matrix is composed of the average stiffness matrix of the structure [Ks] assembling the torsional stiffness matrix of shafts [Kθ] and the stiffness matrix of bearings [Kp].
[Kp] is the matrix stiffness of the bearings, and can be written as follows [24]:
[Kθ] is the torsional stiffness matrix of the shafts, and it is in the following form [24]:
The matrix [K(t)] representing gear mesh stiffness, a critical component in the analysis, varies dynamically over time. It captures the dynamic changes in stiffness during operation, offering valuable insights into the system's behavior over time. The expression for this matrix is as follows [24]:
With:
where [K1(t)] is the first-time varying stiffness.
[K2(t)] is the second-time varying stiffness.
To reduce the vibration level, we applied a proportional damping matrix [C(t)] [25].
With [Kc] is the mean component of mesh stiffness.
The stiffness matrix is composed of the average stiffness matrix of the structure [Ks] assembling the torsional stiffness matrix of shafts [Kθ] and the stiffness matrix of bearings [Kp] [25].
See equation (16) below
with: η and μ are the damping constants defined by: η=10-2, μ=10-5 [25].
The external vector force is defined by:
with: Caer(t) is the aerodynamic torque and Cgen(t) is the generator torque.
Under standard operation conditions, the system is subjected to excitations from both external and internal sources. The primary factors contributing to these excitations are the variability of the wind resources and the fluctuation of the gear mesh stiffness as mentioned by [25]. However, for the purposes of the present study, only wind excitation is considered. Consequently, the wind turbine speed Ωwt is assumed to remain constant Ωwt = 13rad/s, representing an average wind magnitude level Vmoy =12m/s.
The wind velocity is expressed as below [25].
where (ω1=π) and (ω2=2π) represent the angular frequencies (rad/s).
Under these conditions, the instantaneous aerodynamic torque is given as follows.
With: Cp, R and ρair represent respectively the power coefficient, the rotor radius, and the air density.
The generator torque Cgen(t) is dependent on the aerodynamic torque Caer(t) and the gearbox ratio. It is defined by:
where ηgear represent the gear ratio and is calculated as follows:
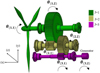 |
Fig. 1 Global dynamic system including gear box. |
2.1.2 Gear box geometry
The gear system under consideration comprises four gears and three shafts. The overall volume of the model is determined by these components, which are categorized based on their shape and type. Both the shafts and gears have a cylindrical shape, and their volumes are calculated as the product of their cross-sectional area and length. Figure 2 illustrates the two-stage spur gear being studied, along with the key measurements. The dimensions of the gearbox are represented by the length (L) and width (w). The input to the gearbox is provided by the shaft length Lint, and the output is connected to the shaft Lout The diameters of the three shafts are denoted as ds1, ds2, ds3, refer respectively the first shaft diameter, the second shaft diameter, the third shaft diameter. The face widths of the first and second stage gears are represented as b1,b2
 |
Fig. 2 Typical two stage spur gear. |
2.2 Problem set- up
The objective of this study is to address the challenges associated with designing a reliable two-stage spur gear while simultaneously minimizing its total volume and center distance. To achieve this, the study proposes an approach that integrates the gear's reliability degree into the optimization process. The paper discusses two cases of multi-objective optimization: the first approach is based on traditional deterministic design optimization (DDO) using the non-sorting algorithm II (NSGA-II). The second is a multi-objective optimization based on reliability analysis (MORBDO) using the constrained non-dominated genetic sorting algorithm (C-NSGA-II).
As regards multi-objective genetic algorithms, NSGA-II is widely preferred because of its ability to converge rapidly and maintain diversity within the population. This diversity is achieved through a positioning concept based on the degree of non-dominance of solutions, resulting in a uniform distribution of solutions along the Pareto front, as shown in Figure 3. The NSGA-II algorithm starts with a random population, and the objective functions are evaluated for each solution. The entire population is then ranked based on their degree of non-domination, resulting in different non-domination ranks. A lower rank indicates a more suitable (non-dominated) member, while a higher rank indicates a dominated member.
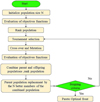 |
Fig. 3 NSGA-II flowchart. |
2.2.1 Objective functions
In this study, two key objective functions are explored. The first function, f1(x), is to minimize the total volume, and the second is to minimize the center distance. The f1 function is defined by the sum of the volumes of both gears Vgears and shafts Vshafts. Due to its non-standardized form, the volume of the gearbox frame is excluded from this evaluation. Consequently, the total volume considered for optimization includes only the volume of gears and shafts.
With:
In this context, the variable n represents the number of stages in the gearbox, while b, d, and ds refer to the face width, gear diameter and shaft diameter. To calculate the width of the gearbox, denoted as ω and determined based on the second shaft, the following equation is applied.
e1,t and xg correspond respectively to the distance between the walls and the gear, the wall thickness of the gearbox and the distance between two gears and are fixed at 10 mm [2].
In equation (15), the crossover length of the input shaft Lint and the output shaft Lout outside the gearbox frame is taken to be twice of the input shaft diameter ds1 and the output shaft diameter ds1 [2].
The second one consists of minimizing the center distance.
As shown in Figure 2, the term of center distance in gear transmissions means to the perpendicular distance between the input shaft ds1 and the output shaft ds3. This distance is calculated by summing up the radii of the corresponding pinion and gear. The pitch diameter of the gear is obtained by multiplying the modulus (m) and the number of teeth of the pinion (Z). In the case of multi-stage gear systems, such as the one studied in this article, the total distance is obtained by summing up the different stages of the gearing. CD noted this concept in the article.
With:
m1 and m2 are respectively the modulus of the first and the second stage gearbox.
Z12,Z21,Z31,Z32 are the teeth number for the first and the second gearbox stage.
The aim of multi-objective optimization here is to ensure effective minimization of the first objective function. Since we already know that if we get an optimal total volume, we'll also get an optimal Center Distance (CD).
2.2.2 Design constraints
The requirements imposed as part of this study are geometric requirements. They are based on the geometric shapes of the parts.
To eliminate interference, the radius of gear 21 must always be smaller than the radius of gears 22 and 31, minus the radius of the output shaft, as shown in the formula below:
The width of the gear face b, expressed in respect of the modulus can be defined by the following formula.
Under practical conditions, a contact ratio greater than 1,2 is recommended, as it is often reduced due to assembly inaccuracies. It can also cause an increase in vibration and noise of the system. For this reason, another function constraint is added to the algorithm.
-
Consequently, the total calculated volume f1 must be less than the maximum allowed volume Vmax of the gearbox. Vmax is limited to 10*107 mm3.
The efficiency of a gear transmission should fall within the range of 95% to 98%.
2.2.3 Design variables
The optimization conducted in this article, incorporating uncertainty associated with all decision parameters, is also combinatorial in nature. The eleven potential design variables, encompassing the modules of the first and second stages, m1,m2 the number of gear teeth Z12, Z21, Z22, Z31, shaft diameters ds1, ds2, ds3, as well as gear widths b1,b2 are all addressed within this optimization framework. The specified thresholds and permissible variable types, outlined in Table 1, are applied to account for the inherent uncertainty in these parameters. These considerations are integrated into the subsequent multi-objective optimization analyses presented in the article. The design variables x for the two-stage gearbox are formulated as follows.
Random design variables properties.
2.2.4 Multi-objective reliability-based design optimization
Unlike traditional Multi-Objective Optimization (MOO), Multi-Objective Reliability Based Design Optimization (MORBDO) focuses on attaining an optimal trade-off between multiple objective functions while considering the uncertainty associated with variables and design parameters. This approach ensures that the resulting solutions not only optimize the objectives but also account for the inherent variability and uncertainties in the system.
where x and y represent the design and the random variables, Pr[.] and 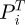 . are respectively the probability operator and the target failure probability.
. are respectively the probability operator and the target failure probability.
2.2.4.1 Standard approach
The (RBDO) problem is typically formulated using the conventional approach, considering two spaces: the physical space, which represents the design variables in their original units, and the normalized space, where the design variables are normalized or transformed as illustrated in Figure 4.
The conventional formulation addresses two distinct problems:
The optimization problem: the main objective is to minimize the function f(x), subjected to deterministic constraints gk(x) and reliability requirements.
Here u is the modulus of the vector in normal space,β(x, μ) is the reliability index of the system and βt is the theoretical reliability.
To calculate the reliability index, which corresponds to the minimum distance between the origin and the limit state function H(x, μ) the minimization equation below is solved.
Due to the large number of numerical calculations needed to be executed on both spaces, the classical approach is known to demand considerable computational time. As a result, a more effective technique known as the hybrid method [26] has been developed to alleviate this issue.
 |
Fig. 4 Physical and normalized space. |
2.2.4.2 Hybrid method (HM)
To offset the significant computational time needed for the classical approach, the hybrid method was introduced, as demonstrated by [27] Within the MORBDO problem, the hybrid method can be described as follows:
In this scenario, the reliability target is represented by βt and dβ(x,y) signifies the desired distance between the design points and the optimal solutions. The objective function is minimized within a hybrid design space that encompasses both deterministic variables denoted as x and random variables denoted as y [28]. Figure 5 provides an illustrative example of an HDS for a normal distribution involving two random variables. In the figure, the reliability levels denoted as dβ are visually depicted using ellipses. Additionally, Figure 5 clearly highlights two significant points: the optimal solution denoted as . and the most probable point denoted as
. and the most probable point denoted as  , which can be identified at the intersection of the curve G(x,y)=0 and the reliability limit dβ =βt.
, which can be identified at the intersection of the curve G(x,y)=0 and the reliability limit dβ =βt.
3 Results and discussion
In this section, the results of the deterministic design optimization are first presented. Two optimal design models will be presented, each based on a different input speed. Using the results of this first optimization phase, a multi objectives reliability-based design optimization will be performed to assess the influence of geometric parameter uncertainty on the optimization process. The second part of our study begins with a final check of compliance with design requirements and constraints, both in terms of reliability index and system efficiency.
3.1 Deterministic multi-objective Design optimization
The multi-objective optimization method used enabled us to check the reliability of the numerical code developed to handle the problem studied in this work, and to ensure that it respected the expected results (i.e. maximizing center distance leads to maximizing volume, and vice versa). This approach made it possible to evaluate several criteria simultaneously, and to explore optimal solutions in the light of various complementary or converging objectives. In addition, trade-offs between minimizing the center distance and total volume were effectively evaluated, while considering the specific constraints and preferences inherent in the problem.
To optimize multiple objectives, two different input speeds, 1200 rpm and 1500 rpm, were considered using both the non-dominated sorting genetic algorithm (NSGA-II). The simulations were performed in MATLAB software on a DELL Intel core i7 computer. It should be noted that the consideration of two different input speeds allowed for a more comprehensive optimization of the objectives and leads to a better overall performance of the two-stage spur gear. Table 1 displays the upper and lower bounds of each parameter, presenting the range within which they were varied during the optimization process. Meanwhile, Table 2 provides a list of the various operating conditions that were tested in the optimization process.
Figure 6 and 7 illustrate the respective Pareto Fronts for the two studied cases with NSGA-II (1200 rpm and 1500 rpm). The comparison between two distinct input speeds is shown. Overall, both cases demonstrate a similar trend in terms of center distance. However, it is observed that at a low-speed of 1200 rpm, the minimum volume obtained is higher than that of the minimum volume obtained at 1500 rpm. This is clearly evident from the comparison of the Pareto Fronts shown in Figure 6 and 7.
However, it is observed that at a low-speed of 1200 rpm, the minimum volume obtained is higher than that obtained at 1500 rpm. This difference is clearly evident from the comparison of the Pareto Fronts shown in Figure 6 and 7.
Table 3 provides the optimal values of the design variables considered in the multi-objective optimization.
Operating conditions.
 |
Fig. 6 Pareto front NSGA-II_1200 rpm. |
 |
Fig. 7 Pareto front NSGA-II_1500 rpm. |
Optimal designs variables for two input speed using NSGA-II.
3.2 Multi objective reliability-based design optimization
The reliability optimization result is achieved through the hybrid method (HM) in conjunction with the C-NSGA-II developed by [6]. To minimize the solution space, the problem parameters are subjected to lower and upper bounds, as presented in Table 1. A comparison between six population sizes is detailed in Table 4, which show the optimal values of the design variables resulting in the reliability multi-objective optimization for each of the six different population sizes. Here, the target reliability level is taken βt=3 which corresponds to a failure probability about 10-3. In comparison to the deterministic optimization studied in the first sub-section and based on its results, the input speed in this section was determined to be 1500 rpm.
Figure 8 presents the Pareto front C-NSGA-II for 300 populations, illustrating the optimal objective functions of the converged model. When comparing these optimal objective functions with those obtained from the deterministic optimization, which ran at 1500 rpm using NSGA-II, a slight difference is observed in the minimum volume achieved.
The minimum volume obtained using C-NSGA-II is slightly higher compared to the one obtained through deterministic optimization. However, the minimum center distance is lower than that achieved through deterministic optimization using NSGA-II.
By examining Table 5, it is observed that, as the population size increases, the values of the overall optimal objective function improve. This indicates that larger populations allow for a more thorough exploration of the design space, leading to better design solutions. The lower values of the objective function imply that the optimized designs exhibit improved performance. Additionally, the converged reliability index (β), is provided in Table 5. It reflects the level of reliability achieved in meeting the specified performance constraints. A higher value of the reliability index indicates a higher level of reliability. It can be observed that larger population sizes (300) result in higher reliability index, indicating that the optimized designs are more reliable in meeting the performance criteria.
Figure 9a and 9b complements the findings from Table 6 by visually displaying the trend. The graph illustrates how the overall optimization of the converged reliability index vary with different population sizes. It shows a clear trend where larger population sizes correspond to lower values of the reliability index (β) which approaches to 3. Based on these findings, it can be concluded that larger population sizes are more favorable for achieving better optimization results and improved reliability.
Figure 10 represents the efficiency histogram, which shows the distribution of the efficiency values obtained from our model. The histogram shows a narrow distribution centered on the specified efficiency range [95–98%]. This implies that the majority of the gear configurations generated by the model satisfy the efficiency constraints, indicating a high level of reliability. The narrow distribution indicates also that there is minimal variation in efficiency among the generated gear configurations. The concentration of values within the specified range suggests that the design optimization process has been successful in producing reliable gear configurations that meet the desired efficiency criteria.
Indeed, the fact that most of the efficiency values fall within the specified range is promising from a design perspective. It implies that the optimized gear configurations are likely to exhibit consistent and reliable performance in terms of efficiency. This is crucial for the effective operation of the two-stage wind turbine gear system.
Optimal design parameters for different population size using C-NSGA-II.
 |
Fig. 8 Pareto front C-NSGA-II for 300 populations. |
Optimal objectives functions for different population size using C-NSGA-II.
 |
Fig. 9 (a) Effects of population size on the reliability index, (b) 3D visualization. |
 |
Fig. 10 Distribution of the efficiency values. |
4 Conclusion
This paper presents a Multiobjective Reliability-Based Design Optimization (MORBDO) technique for optimizing of the internal geometric parameters of a two-stage wind turbine spur gear. The primary objectives of this study are to minimize the total volume and center distance of the gear system. Notably, the proposed approach takes into account the uncertainty associated with the geometric parameters of the wind turbine gear system. The results obtained from the MORBDO approach demonstrate its effectiveness in generating reliable Pareto solutions. The combination of the hybrid method (HM) and the C-NSGA-II algorithm successfully produces well-distributed solutions, considering the required reliability levels. Furthermore, these optimized solutions contribute to enhancing the overall performance of the gear system. The MORBDO technique presented in this paper offers valuable insights into optimizing the internal geometric parameters of two-stage wind turbine spur gears. By considering reliability and employing a multi-objective optimization framework, this approach provides a robust methodology for achieving improved performance and addressing uncertainties in wind turbine gear systems.
Funding
No funding was received for conducting this study.
Conflicts of Interest
The authors state that they don't have any conflicts of interest with respect to the research, authorship, or publication.
Data availability statement
All data generated or analyzed during this study are included in the present article.
Author contribution statement
Bilel Karmi: Writing − original draft, Validation, Methodology, Investigation, Formal analysis. Abdelghani Saouab: Writing − review & editing, Validation, Supervision, Methodology. Ahmed Guerine: review & editing. Slim Bouaziz: Writing − review & editing, Validation, Supervision, Methodology. Abdelkhalek El Hami: Writing − review & editing, Validation, Supervision, Methodology. Mohamed Haddar: Writing − review & editing, Validation, Supervision, Methodology. Khalil Dammak: software, Methodology.
References
- K. Tamboli, S. Patel, P.M. George, R. Sanghvi, Optimal design of a heavy-duty helical gear pair using particle swarm optimization technique, Proc. Technol. 14, 513–519 (2014) [CrossRef] [Google Scholar]
- M. Patil, P. Ramkumar, K. Shankar, Multi-objective optimization of the two-stage helical gearbox with tribological constraints, Mech. Mach. Theory 138,38–57 (2019) [CrossRef] [Google Scholar]
- E.S. Maputi, R. Arora, Multi-objective optimization of a 2-stage spur gearbox using NSGA-II and decision-making methods, J. Braz. Soc. Mech. Sci. Eng. 42,1–22 (2020) [CrossRef] [Google Scholar]
- T.H. Chong, I. Bae, A. Kubo, Multiobjective optimal design of cylindrical gear pairs for the reduction of gear dize and meshing vibration, JSME Int. J. Ser. C. 44, 291–298 (2001) [CrossRef] [Google Scholar]
- B.A. Abuid, Y.M. Ameen, Procedure for optimum design of a two-stage spur gear system, JSME Int. J. Ser. C. 46, 1582–1590 (2003) [CrossRef] [Google Scholar]
- K. Deb, A. Pratap, S. Agarwal, T. Meyarivan, A fast and elitist multiobjective genetic algorithm: NSGA-II, IEEE Trans. Evol. Comput. 6, 182–197 (2002) [Google Scholar]
- H.-Z. Huang, Z.-G. Tian, M.J. Zuo, Multiobjective optimization of three-stage spur gear reduction units using interactive physical programming, J. Mech. Sci. Technol. 19, 1080–1086 (2005) [CrossRef] [Google Scholar]
- C. Gologlu, M. Zeyveli, A genetic approach to automate preliminary design of gear drives, Comput. Ind. Eng. 57, 1043–1051 (2009) [CrossRef] [Google Scholar]
- F. Mendi, T. Başkal, K. Boran, F.E. Boran, optimization of module, shaft diameter and rolling bearing for spur gear through genetic algorithm, Expert Syst. Appl. 37, 8058–8064 (2010) [CrossRef] [Google Scholar]
- N. Marjanovic, B. Isailovic, V. Marjanovic, Z. Milojevic, M. Blagojevic, M. Bojic, A practical approach to the optimization of gear trains with spur gears, Mech. Mach. Theory 53, 1–16 (2012) [CrossRef] [Google Scholar]
- S. Golabi, J.J. Fesharaki, M. Yazdipoor, Gear train optimization based on minimum volume/weight design, Mech. Mach. Theory 73, 197–217 (2014) [CrossRef] [Google Scholar]
- V. Savsani, R.V. Rao, D.P. Vakharia, Optimal weight design of a gear train using particle swarm optimization and simulated annealing algorithms, Mech. Mach. Theory 45, 531–541 (2010) [CrossRef] [Google Scholar]
- A. Parmar, P. Ramkumar, K. Shankar, Macro geometry multi-objective optimization of planetary gearbox considering scuffing constraint, Mech. Mach. Theory 154, 104045 (2020) [CrossRef] [Google Scholar]
- L. Qi, J. Zhou, H. Xu, Multi-objective optimization of gearbox based on panel acoustic participation and response surface methodology, J. Low Freq. Noise Vib. Act. Control. 41, 1108–1130 (2022) [CrossRef] [Google Scholar]
- Y. Lei, L. Hou, Y. Fu, J. Hu, W. Chen, Research on vibration and noise reduction of electric bus gearbox based on multi-objective optimization, Appl. Acoust. 158, 107037 (2020) [CrossRef] [Google Scholar]
- K. Dammak, A. Baklouti, A. El Hami, Optimal reliable design of brake disk using a Kriging surrogate model, Mech. Adv. Mater. Struct. 29, 7569–7578 (2022) [CrossRef] [Google Scholar]
- S. Barakat, K. Bani-Hani, M.Q. Taha, Multi-objective reliability-based optimization of prestressed concrete beams, Struct. Saf. 26, 311–342 (2004) [CrossRef] [Google Scholar]
- Y. Zhang, X. Xu, G. Sun, X. Lai, Q. Li, Nondeterministic optimization of tapered sandwich column for crashworthiness, Thin Walled Struct. 122, 193–207 (2018) [CrossRef] [Google Scholar]
- R.H. Lopez, A.J. Torii, L.F.F. Miguel, J.E.S. De Cursi, An approach for the global reliability-based optimization of the size and shape of truss structures, Mech. Ind. 16, 603 (2015) [CrossRef] [EDP Sciences] [Google Scholar]
- O. Braydi, C. Gogu, M. Paredes, Robustness and reliability investigations on a nonlinear energy sink device concept, Mech. Ind. 21, 603 (2020) [CrossRef] [EDP Sciences] [Google Scholar]
- J. Zhou, S. Huang, Y. Qiu, Optimization of random forest through the use of MVO, GWO and MFO in evaluating the stability of underground entry-type excavations, Tunn. Undergr. Spac Technol. 124, 104494 (2022) [CrossRef] [Google Scholar]
- J.J. Eckert, S.F. da Silva, F.M. Santiciolli, Á.C. de Carvalho, F.G. Dedini, Multi-speed gearbox design and shifting control optimization to minimize fuel consumption, exhaust emissions and drivetrain mechanical losses, Mech. Mach. Theory 169, 104–644 (2022) [Google Scholar]
- J. Stefanović-Marinović, Ž. Vrcan, S. Troha, M. Milovančević, Optimization of two-speed planetary gearbox with brakes on single shafts, Rep. Mech. Eng. 3, 94–107 (2022) [CrossRef] [Google Scholar]
- I. Mabrouk, A. El Hami, L. Walha, B. Zghal, M. Haddar. Dynamic vibrations in wind energy systems: application to vertical axis wind turbine, Mech. Syst. Signal Process. 85, 396–414 (2017) [CrossRef] [Google Scholar]
- K. Abboudi, L. Walha, Y. Driss, M. Maatar, T. Fakhfakh, M. Haddar, Dynamic behavior of a two-stage gear train used in a fixed-speed wind turbine, Mech. Mach. Theory 46, 1888–1900 (2011) [CrossRef] [Google Scholar]
- G. Kharmanda, A. Mohamed, M. Lemaire, Efficient reliability-based design optimization using a hybrid space with application to finite element analysis, Struct. Multidiscip. Optim. 24, 233–245 (2002) [CrossRef] [Google Scholar]
- K. Dammak, A. El Hami, Thermal reliability-based design optimization using Kriging model of PCM based pin fin heat sink, Int. J. Heat Mass Transf. 166, 120745 (2021) [CrossRef] [Google Scholar]
- K. Dammak, A. Yaich, A. El Hami, L. Walha, M. Haddar, An efficient optimization based on the robust hybrid method for the coupled acoustic–structural system, Mech. Adv. Mater. Struct. 27, 1816–1826 (2020) [CrossRef] [Google Scholar]
Cite this article as: B. Karmi, A. Saouab, A. Guerine, S. Bouaziz, A. EL. Hami, M. Haddar, K. Dammak, Reliability based design optimization of a two-stage wind turbine gearbox, Mechanics & Industry 25, 16 (2024)
All Tables
All Figures
 |
Fig. 1 Global dynamic system including gear box. |
| In the text | |
 |
Fig. 2 Typical two stage spur gear. |
| In the text | |
 |
Fig. 3 NSGA-II flowchart. |
| In the text | |
 |
Fig. 4 Physical and normalized space. |
| In the text | |
 |
Fig. 5 Hybrid design space for normal distribution [28]. |
| In the text | |
 |
Fig. 6 Pareto front NSGA-II_1200 rpm. |
| In the text | |
 |
Fig. 7 Pareto front NSGA-II_1500 rpm. |
| In the text | |
 |
Fig. 8 Pareto front C-NSGA-II for 300 populations. |
| In the text | |
 |
Fig. 9 (a) Effects of population size on the reliability index, (b) 3D visualization. |
| In the text | |
 |
Fig. 10 Distribution of the efficiency values. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.