| Issue |
Mechanics & Industry
Volume 21, Number 2, 2020
|
|
|---|---|---|
| Article Number | 206 | |
| Number of page(s) | 11 | |
| DOI | https://doi.org/10.1051/meca/2019056 | |
| Published online | 07 February 2020 | |
Regular Article
Variational approach for mechatronic tolerancing: application to a DC motor
1
QUARTZ Laboratory, The School of Mechanical Engineering of Paris (SUPMECA), 3 rue Fernand Hainaut, 93400 Saint-Ouen Cedex, France
2
Laboratory of Mechanics, Modeling and Production, National Engineering School of Sfax (ENIS) BP, 1173-3038 Sfax, Tunisia
* e-mail: hana.siala@supmeca.fr
Received:
9
October
2017
Accepted:
31
May
2019
Having an increasingly complex set of inter-relations between several components from different domains, mechatronic systems become more and more complex. The behavior of such systems depends on the values of their parameters and variables. A deviation of these values from their expected values affects the overall functioning of the system, degrades the system quality, and may be a significant threat to safety. To reach an expected quality level, the deviations between actual and target values of parameters should be within specified tolerances. For this, two extreme limits (i.e. upper and lower bounds) of these values must be wisely determined. It is also important to know the impact of parameters deviations on system behavior. Furthermore, the margin of variables should be controlled to evaluate system performance with respect to the specifications, requirements and user needs. This paper describes a methodology based on a variational approach combined with Worst-Case Analysis and Monte Carlo Simulation to determine the impact of the parameters variation on the system behavior. It helps designers to analyze tolerances of mechatronic systems. Our proposed methodology is illustrated with a DC motor case study. The results show that the developed method provides a new way for mechatronic tolerancing.
Key words: General tolerance / parameter variation / variational approach / sensitivity / mechatronic design
© AFM, EDP Sciences 2020
1 Introduction
Complex system design requires rigorous approaches to satisfy a set of requirements including cost and quality especially in the presence of uncertainties, which is unavoidable in the realization of systems. Uncertainty is defined as a lack of knowledge or a state of being unsure of something. For example, the real parameters of components differ from their expected nominal values. This is due to disturbance factors such as differences in manufacturing techniques and environmental conditions. Furthermore, these parameters can vary over time. They fluctuate around their nominal values due to several factors such as wear, fatigue or thermal effect. Thus, in this paper, a parametric variation is defined as a deviation of the real value from the expected value of a parameter. To fulfill the proper function, these variations should be restricted by tolerances, which are the allowable deviation. When parameter values deviate from their tolerances levels, it may introduce risks and failure to conform specifications. Therefore, it is compulsory to specify the appropriate parameters tolerances that ensure the proper function of the system. Tolerances are used to cover uncertainties caused by the deviations of parameters and variables. It aims at developing a robust design insensitive to variations. Similarly, the margin is the permissible variation; it is the allowance to move within limits. The main difference between tolerance and margin is that the tolerance refers to the permissible limits of variation in a physical dimension or property and the margin is used in different fields to any limit condition. The margin is a generic term for tolerance, which is an engineering vocabulary [1].
In mechanical engineering, tolerancing deals with dimensional and geometric tolerances. In the ASME standard [2], it is defined as the total amount that a dimension is permitted to vary.
However, traditional geometric tolerances are no longer sufficient for mechatronic systems because of the numerous interactions and complex relations between mechanical, electrical and control components. It is, therefore, necessary to extend mechanical tolerancing to mechatronic tolerancing. This latter is defined by Zerelli et al. [3] as the combination of several types of tolerances (e.g. in mechatronic systems, a variation of a mechanical parameter and an electrical one can both be included).
In this paper, a technique based on a variational approach is proposed to evaluate the influence of the parameters variations on the system behavior in order to improve mechatronic system design.
The remaining of this paper is organized as follows: Section 2 is devoted to present an overview of parameters variation and some existing works on tolerancing of mechatronic systems. Then, the proposed developed approach is described in Section 3. It is applied in Section 4 to a DC motor. Finally, Section 5 gives conclusions and some future work.
2 Parameters variation and tolerancing of mechatronic systems: state of the art
The behavior of a mechatronic system can deviate from the desired one due to deviations of some parameters from their expected values. The minor fluctuations, in a mechatronic system, may generate system failure. Systems that are designed without paying attention to the variations process are the most likely to fail in meeting the desired requirement (power, timing, stability, and quality) [4]. Thus, the consequences of these variations must be analyzed by integrating mechatronic tolerancing during the design process and the design should be robust against parameter variations, which can affect mechanical as well as electronic components.
Different research works have been developed to predict the effects of parameters variations and discuss mechatronic tolerancing. In the following, we bring a body of literature approaching this subject:
According to Aubin et al. [5], the functioning of a mechatronic system depends on the behavior of its components. An infinitesimal variation of one component can considerably affect the global functioning of the system. A general way of modeling these systems parameters variations is to use differential equations: each variation of one parameter introduces a variation of its corresponding coefficient on the differential equation. The authors used differential inclusion as a framework to model systems parameters variations. It is a generalization of differential equations. The main application of this method is the analysis of parametric variation in dynamics system and the result is a reachable set of trajectories, which includes all possible solutions in the state-space. As a continuation of these works, the authors in [6,7], inserted the impulse differential inclusion to model parametric variations in a hybrid system. The behavior of such a system consists in discrete jumps between continuous states. However, it cannot be developed to study a closed-loop control.
El Feki [8] modeled the system using the inverse of Bond Graph to determine the unknowns of problems. This modeling reduces the number of iterations. The author used the probabilistic approach to calculate tolerance. This approach seems interesting since it associates a probability description (probability density function) with each variable in the model and it measures the effect of different uncertainties of every system element. Nguyen [9] has developed El Feki's work by using a technique combining fuzzy logic and the inverse of Bond Graph formalism. However, this method requires the model to be invertible.
In the same context, Jabali et al. [10] and Jouilel et al. [11], proposed another approach of mechatronic tolerancing. It consists in modeling the system using Bond Graph approach and applying Monte Carlo simulation. It is applied in the case of the slider-crank system driven by a gear motor. This approach allows the analysis and synthesis of mechatronic system tolerances on the relative position of the piston to the crankshaft axis. However, since parameters are randomly distributed, there is a risk of neglecting influential variations on the system behavior.
These aforementioned research works focus only on the consistency of the output response. Thus, they are single-objective methods. Working conditions of the components (such as voltage, current, etc.) are not considered. Therefore, in this paper, a variational approach is chosen in a multi-objective tolerance design to improve robustness of a mechatronic system. It does not only focus on maintaining the system output in a specified tolerance but also on keeping working conditions in expected margins.
Our proposed tolerancing approach is adopted from the variational association used in the mechanical domain. The association is a geometrical fitting operation [12], which is used to adjust nominal elements to real elements. It is a crucial operation to define datum and tolerance position, which defines allowable deviations in the relative position of the center, the axis, or the median plane of a feature depending on its geometrical shape.
Choley et al. [13–15] proposed a new variational association process to verify geometrical specifications. In this work, the authors defined the association operation of the ideal geometry with the actual geometry as a variation of the defined parameters of the nominal geometry in order to minimize the deviation between the real and the expected nominal geometries. To describe the problem mathematically, a Variational Distance Function is proposed to associate the ideal geometry to the actual geometry with a variational association process. This process consists in changing the parameters to best fit the nominal geometric element with the measured points. As this method is a purely mathematical task, we propose to apply it to multiphysics systems (mechatronic systems) integrating electronics, electromagnetism, hydraulic, etc., in order to evaluate the global behavior of the system. In this case, each physical parameter or variable (resistance, torque, speed, current, etc) can be treated as an intrinsic parameter. Thus, our contribution is to propose a method based on the “variational approach” to determine the influence of parameter variations on the system behavior and define the allowable tolerances on these parameters to keep the system behavior compliant with the specifications.
3 Proposed method: variational approach
To study a mechatronic system, the following variables [16] are introduced:
-
Design parameters: let's consider P the vector of m design parameters denoted by P1 through Pm . They describe the system characteristics (mechanical, electrical, control…). However, they are subject to variations due to manufacturing errors, wear, or other uncertainties. The number of parameters can vary from one system to another depending on its complexity.
-
Performance variables: the performance is evaluated with respect to n variables denoted by V1 through Vn , assembled in vector V. The performance specifications are not limited to control type performance measures (speed of response, disturbance rejection, steady-state error…), they also include working conditions (voltage, current, angular speed, etc).
To define the behavior of the complex system, S (V, P) is proposed to be the system of physical equations. In a nominal case, the system is specified by target values of variables V and parameters P. But in a real case, the system is characterized by the actual values of variables V′ and parameters P′ . Thus, it is defined by S (V ′, P′ ) =S (V + dV, P + dP).
The deviation between S (V, P) and S (V + d
V, P + dP) should be specified and reduced. To quantify this deviation mathematically, we propose to differentiate S (V, P) with respect to the m parameters Pi (i = 1 to m) and to the n variablesVj (j = 1 to n). That is mean to calculate dS (V, P) as follows: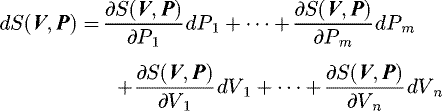 (1)
(1)
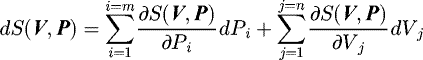 (2)
(2)
To minimize it, we rget and then assume that dS (V, P) = 0.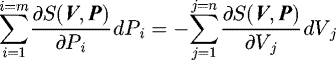 (3)with d
V
j
: tolerances on each variable; d
P
i
: tolerances on system parameters.
(3)with d
V
j
: tolerances on each variable; d
P
i
: tolerances on system parameters.
While the system is continuous, the same equations are found at every particular instant. Thus, for a system defined with m parameters and n variables, the previous equations are the same at z instants (the chosen z time instants should be greater than the number of parameters and variables). Therefore, the following matrix equation can be deduced:
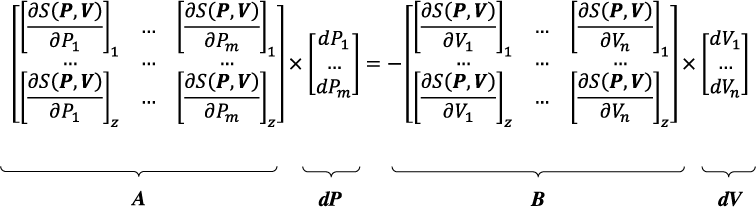
It can be presented in this simplified form: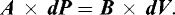 (4)
(4)
The next step is to complete matrices A and B numerically. Thus, to perform the physical behavior of the mechatronic system, multi-domain tools or languages can be used such as Matlab/Simulink, Bond Graph or Modelica.
As the compliance with mathematical modeling should be guaranteed, the Modelica language including a mathematical description of the models [17–20] has been selected. In parallel, as the Dymola tool implements Modelica while providing a graphical interface, it will be chosen as the multidisciplinary modeling tool. It is commonly used for the modeling and simulation with major applications in virtual prototyping. The target values of variables are given with the Modelica simulation. We extract variables in z instants and insert them in the matrices A and B.
After obtaining the complete matrix formulation, it can be solved in two ways:
-
With regards to the requirements: knowing the acceptable deviation on the behavior of each variable (dV), the admissible tolerances of parameters (dP) can be searched. In this case, we need to invert the matrix A.
-
With regards to the specifications: the system components have been chosen with given parameters tolerances (dP). Then, we estimate their impact on the deviation of variables (dV). Tolerances can be analyzed to evaluate system performance. In this case, the matrix B should be inverted.
The first case is discussed in [21,22]. In this paper, the second case is taken into consideration. Thus, dP is supposed to be known and our objective is to determine their effect on the deviation of variables dV. Therefore, we need to invert the matrix B.
The system of equations in which B is a rectangular z×n-matrix is an overdetermined system with more equations than unknowns (z >n). There is more equations than unknowns since z repeated evaluations are taken to minimize errors. The method of least squares is a way of solving an overdetermined system of linear equations. It helps us to obtain dV the unique vector which minimizes ||A . dP − B . dV||, or equivalently, which minimizes ||A . dP − B . dV||2 [23].
This solution is given by using the pseudo-inverse of Moore-Penrose.
3.1 Moore-Penrose pseudo-inverse resolution [23]
The pseudo-inverse M + is defined for all matrices M, even if they are not square matrices or not full rank matrices. There is precisely one matrix M +. When matrix M is a full rank matrix, the pseudo-inverse M + can be expressed as a simple algebraic formula:
-
When M has linearly independent columns (thus matrix M T M is invertible), M + can be computed as:
 (5)
(5)
This particular pseudo inverse is a left inverse and in this case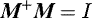 (6)
(6)
-
When M has linearly independent rows (thus matrix MM T is invertible), M can be computed as:
 (7)
(7)
This is a right inverse, thus MM+ = I.
In our case, the number of rows is greater than the number of columns. Thus, the Moore-Penrose pseudo-inverse gives: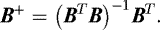 (8)
(8)
Thus, the deviations of variables dV are calculated based on parametric variations dP as shown in equation
(9):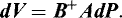 (9)
(9)
It is crucial to analyze the impact of parameters tolerances dP on the variables deviations dV. The most commonly utilized approach is the Worst-Case analysis [24,25] and Monte Carlo analysis [26]. The Monte Carlo is a statistical method, which analyzes the variables deviations by sampling parameters with probability distributions. Its result is more realistic but it consumes much more computing time. The Worst-Case analysis evaluates the variables deviations under a set of worst case parameters deviations. The result can verify whether the variables deviations are acceptable under worst case or not. This method has the advantage of reducing the computing time, but the result is too conservative. For different purposes, these two methods are adopted in this research.
To conclude, Figure 1 describes the proposed tolerancing approach:
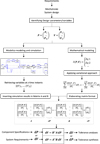 |
Fig. 1 Flowchart of the process of general tolerance for mechatronic system using variational approach. |
4 Use case: DC motor
The proposed approach is illustrated with a DC motor. It is an electromechanical system. The driven load is an oscillatory torque.
4.1 Variables and parameters of the system
In order to solve the system the following variables need to be identified:
Let  be the vector of variables where U is the voltage (V), I is the current (A), ωm is the angular speed (rad.s−1) and Cr is the load torque (N.m).
be the vector of variables where U is the voltage (V), I is the current (A), ωm is the angular speed (rad.s−1) and Cr is the load torque (N.m).
Let 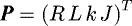 be the vector of parameters where R is the resistance (Ω), L is the inductance (H), k is the “torque” constant and J is the inertia moment (kg.m2).
be the vector of parameters where R is the resistance (Ω), L is the inductance (H), k is the “torque” constant and J is the inertia moment (kg.m2).
4.2 Equations development
The DC motor is modeled by the following equations: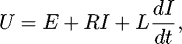 (10)
(10)
 (11)
(11)
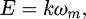 (12)
(12)
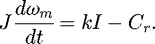 (13)
(13)
The first equation (10) corresponds to the electric behavior of the motor, which is modeled by a resistance R, an inductance L and an electromotive force E arranged in series.
Equations (11) and (12) correspond to the electromechanical coupling. The current in the coil creates a Laplace force, which is reflected by a motor torque Cem. Equation (12) reflects the link between the angular speed ωm and the counter-electromotive force E, through the “torque” constant k.
Equation (13) corresponds to the dynamics equation obtained by isolating the shaft and applying the kinetic energy theorem. It is subject to a motor torque Cem and a load torque Cr.
These equations (10)–(13) can then be combined and expressed with the following equations (14) and (15) related to power, in accordance with the energy conservation, to express S (V, P):
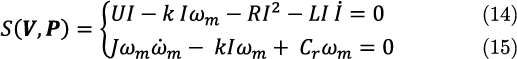
4.3 Application of the variational approach
The differentiation is applied while neglecting the second order. In addition, the variable and parameters variations have been separated.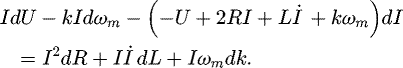 (16)
(16)
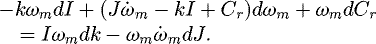 (17)For each chosen instant, we have the same equations. This following matrix format includes all extracted points:
(17)For each chosen instant, we have the same equations. This following matrix format includes all extracted points:
 (18)
(18)
As mentioned below, dP is given by specifications and our objective is to evaluate their effect on the deviation of variables dV and the designer should compare the results with requirements. Therefore, we need to invert the matrix B. Thus, we use the pseudo-inverse of Moore-Penrose as it is mentioned in (8) and (9).
4.4 Modeling and simulation
Figure 2 shows a simple model of a DC motor using Modelica language with the Dymola tool. This model is used to evaluate the variables in the nominal case.
Variables curves in Figure 3 are given via Modelica simulation.
Using Dymola, the number of time intervals is 500 for one second by default. While all the curves of variables are periodic (continued repetition of part) with a period equal to 2 s, the chosen number of instants is z = 500 × 2 =1000.
For each chosen instant in time, the target variables have been retrieved from these curves to apply the approach.
 |
Fig. 2 DC motor model performed with Dymola (Modelica). |
 |
Fig. 3 Variables curves. |
4.5 Sensitivity analysis
Sensitivity analysis [26,27] is used to quantify the impact of parameters variation on the system response. We can deduce the most and the least impacting parameters. The sensitivity to a parameter Pi is the variation of a variable Vj
caused by one unit variation of this parameter. The sensitivity of the variable Vj
to a parameter Pi is calculated as follow: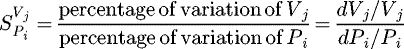 (19)
(19)
For each parameter Pi, we assign a variation of 1% of the nominal value to this parameter while other parameters variations are counted as zero. Then, using equation (9), the sensitivity of each variable to this parameter is evaluated.
Figure 4 defines the sensitivity of each variable according to parameter variations. From these results, we conclude that:
-
A small variation of R or L does not have a great influence on the variables of the system.
-
The torque constant is the most influential element on the system. It affects all variables.
-
The inertia moment has no influence except on the speed of the motor and it has a small influence on the voltage.
In a complex system, it is wasteful to control many parameters. Thus, the sensitivity analysis is used to deduce the most and the least impacting parameters since it is important to limit and control the parameters variations that strongly affect the system behavior. The results of this sensitivity analysis help the designers to make technical decision. In fact, they get an idea about how the chosen solution is sensitive to any change or deviation in one or more parameters.
 |
Fig. 4 Variables sensitivity to parameters variations. |
4.6 Tolerance analysis
In a mechatronic system, the deviation between real and target value of parameters cannot be ignored. It may have a significant effect. After obtaining the complete matrix formulation, we look to analyze the effect of parameters tolerances dP on the variables deviations dV. Thus, we will use the “worst case” analysis and the “Monte Carlo simulation”. In this part, Mathworks MATLAB software is used to make the numerical calculation.
4.6.1 The worst-case analysis
The interval computation [24,28] is an arithmetic method used to solve problems of uncertainty. In our case, a system parameter Pi can be represented in interval form [Pin − ΔPi, Pin + ΔPi] where Pin is the nominal value of Pi and ΔPi is the maximum deviation (tolerances). This interval represents the domain of all possible parameters values associated with their deviations.
Table 1 presents the chosen values of parameters and their tolerances as inputs.
The objective is to determine the variables variations dV. After applying the variational approach, we represent in Table 2 the computation results.
In the presence of these parameters variations, the measured variables shall not deviate from the references ones (represented in Fig. 3) for more than these percentages of the maximum value of each variable. The worst case analysis is used to define the maximum variables deviations. In fact, each dVi is an interval, which limits the corresponding variable deviation. After that, in order to ensure the robustness of design, the designer should verify if these maximal deviations are acceptable or not (deviations should be inside the required tolerances).
Nominal value of parameters and their tolerances.
Calculated variables tolerances.
4.6.2 Monte Carlo analysis
Monte Carlo method can analyze and solve different mathematical and physical problems. It uses pseudo-random generators. The obtained results are more accurate than conventional methods of calculation.
The application of the Monte Carlo method starts with the identification of the relations between inputs and outputs. The next step consists in random a sampling of N values of each input according to a distribution law. N should be large enough to determine accurately the statistical distribution of each output (in our case, N = 10000). The distribution is characterized by a standard deviation (σ) which characterizes the variation or the dispersion of a set of data values around an average or mean value (μ). In our case, σ and μ are specified for the parameters and calculated for the variables.
A normal distribution is chosen for the model parameters deviations. According to this distribution, the relation between tolerance interval (TI) (which is the difference between upper and lower limits) and the standard deviation (σ) is determined by the capability index which is computed as 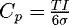 . For a capability index Cp = 1, the production process is generally considered satisfactory and TI = ± 3σ [29] (see Fig. 5). Thus, in these conditions, the standard deviation is defined as
. For a capability index Cp = 1, the production process is generally considered satisfactory and TI = ± 3σ [29] (see Fig. 5). Thus, in these conditions, the standard deviation is defined as 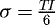 .
.
Moreover, a parameter may be modeled as a combination of its nominal value and a specified deviation as Pi = Pin + dPi.
If Pi is normally distributed around its average Pin , its deviation dPi is also normally distributed around its mean zero.
Therefore, normal distributions for the dP vector are chosen. Table 3 presents the characteristics of the chosen normal distributions, which are applied to the dP vector in the matrix equation (18).
The outputs of this Monte Carlo simulation are the distributions of variables deviations grouped in the dV vector where μ and σ of each deviation are calculated as follows: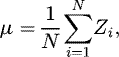 (20)where: Zi is the value of the variable deviation in the ith simulation.
(20)where: Zi is the value of the variable deviation in the ith simulation.
And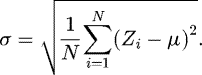 (21)
Figure 6 and Table 4 describe the resulting distributions of the variables deviations.
(21)
Figure 6 and Table 4 describe the resulting distributions of the variables deviations.
These results can provide more instructions for the designers. They should interpret the results and decide if these tolerance ranges are acceptable and do not affect the overall behavior of the system or not.
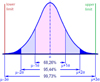 |
Fig. 5 Normal distribution and percentage of trust in a tolerance interval. |
Input of Monte Carlo simulation.
 |
Fig. 6 Variables variations in their tolerance intervals. |
Outputs of Monte Carlo simulation.
4.6.3 Discussion
Comparing the Monte Carlo analysis and worst-case analysis, we find that the statistical TIs are always contained in the arithmetic TIs.
In a worst-case analysis, each variable deviation will have a minimum and maximum value that represent the margin of variation, which should be appropriate with requirements. Worst-case analysis answers the question: if each parameter is affected by its maximum deviation, what are the maximum deviations for the variables? We are therefore dealing with the limits of acceptability and not probability.
Monte Carlo analysis does not focus on the extreme values but focuses on the distribution of the variables deviations. Each parameter will have its own distribution of values based on the manufacturing process, changes in material and environment which contribute to variation in the parameter value. Monte Carlo analysis answers the question: given the distribution of each parameter deviation, what is the probability that variables deviations will be within defined acceptable limits. The result of this method is closer to those under actual condition than for a worst-case analysis but consumes much more computing time.
5 Conclusions and perspectives
Parametric variations are becoming important issues that threat mechatronic systems performances as it is a source of dysfunction of multiphysics systems.
In this paper, the variational approach is used as a framework to model system including parameters and variables variations. It gives a better description of the system behavior with parametric variations. It helps designers to specify and analyze tolerances, in the phase of mechatronic system design, in order to ensure the system quality and performance. The limitation of our proposed approach is that the mechatronic system behavior should be continuous and the deviations are independent.
This approach has been applied to the example of a DC motor considered as a mechatronic system. We will adopt this approach for a more complex example, an electromechanical actuator (EMA) driving an aircraft primary flight control surface (aileron).
Integrating this general tolerance method in systems engineering approach would be an extension to this research. This will help designers in fault detection and in safety and reliability analyses of complex systems.
References
- E. Morse, J.-Y. Dantan, N. Anwer, R. Söderberg, G. Moroni, A. Qureshi, X. Jiang, L. Mathieu, Tolerancing: Managing uncertainty from conceptual design to final product, CIRP Ann. Manuf. Technol. 67, 695–717 (2018) [Google Scholar]
- ASME Y14.5-2009 Dimensioning and tolerancing. The American Society of Mechanical Engineers National Standard, New York, 2009 [Google Scholar]
- M. Zerelli, T. Soriano. Application of impulse differential inclusion for uncertainty analysis of mechatronic hybrid system, in: 9th France-Japan & 7th Europe-Asia Congress on Mechatronics (MECATRONICS)/13th Int'l Workshop on Research and Education in Mechatronics (REM), 2012 [Google Scholar]
- S. Ghosh, K. Roy, Parameter variation tolerance and error resiliency: New design paradigm for the nanoscale era, Proc. IEEE 98, 1718–1751 (2010) [CrossRef] [Google Scholar]
- J.P. Aubin, A. Cellina, Differential Inclusions, Set-Valued Maps And Viability Theory, Springer, Berlin, 1984 [Google Scholar]
- T. Soriano, M. Zerelli, T.H. Gallois, A. Warniez, Quantifying reliability of a mechatronic system using Hausdorff distance in state space, in: 10th France-Japan/8th Europe-Asia Congress on Mechatronics, IEEE, 2014, pp. 47–52 [Google Scholar]
- M. Zerelli, Systèmes mécatroniques à paramètres variables : analyse du comportement et approche du tolérancement, PhD thesis, Ecole Centrale Paris, 2014 [Google Scholar]
- M. El Feki, Analyse et synthèse de tolérance pour la conception et le dimensionnement des systèmes mécatroniques, [Analysis and synthesis of tolerance for the design and sizing of mechatronic systems], thesis, Ecole Centrale Lyon. France, 2011 [Google Scholar]
- V.H. Nguyen, Synthèse de tolérance pour la conception des systèmes mécatroniques: Approche par bond graph inverse, [Tolerance synthesis for the mechatronic systems design: The approach of bond bond inverse], PhD thesis, National Institute of Applied Sciences of Lyon, France, 2014 [Google Scholar]
- M.K. Jabali, M. El Fahime, B. Rzine, M. Radouani, J. Louati, M. Haddar, Computer-aided dimensioning of multi-physics system design in a strategy: Application to a slider crank mechanism, Int. J. Res. Rev. Mechatron. Des. Simul. 1, 1 (2011) [Google Scholar]
- N. Jouilel, M. Radouani, M. El Gadari, E.F. Benaissa, Mechatronic tolerancing: Bond graph approach, Int. J. Adv. Comput. Technol. 5, 2063 (2016) [Google Scholar]
- V. Srinivasan, An integrated view of geometrical product specification and verification, the 7th CIRP International Seminar on Computer Aided-Tolerancing, New York, USA, 2001 [Google Scholar]
- J.Y. Choley, Une approche variationnelle de l'association des références en tolérancement géométrique, PhD thesis, Ecole Centrale Paris, France, 2005 [Google Scholar]
- J.Y. Choley, A. Riviere, Variation of the geometrical parameters for Datums association. Managing geometric uncertainty in the product lifecycle, the 8th CIRP International Seminar on Computer Aided-Tolerancing, Charlotte, North Carolina, USA, 2003 [Google Scholar]
- J.Y. Choley, A. Riviere, A. Clement, et al. A new variational association process for the verification of geometrical specifications, J. Comput. Inf. Sci. Eng. 7, 66–71 (2007) [Google Scholar]
- A.C. Pil, H.H. Asada, Integrated structure/control design of mechatronic systems using a recursive experimental optimization method, IEEE/ASME Trans. Mechatron. 1, 191–203 (1996) [CrossRef] [Google Scholar]
- H. Elmqvist, S. Mattsson, M. Otter, Modelica: The new object-oriented modeling language, in: The 12th European Simulation Multi-conference, Manchester, UK, 1998 [Google Scholar]
- M. Hammadi, J.Y. Choley, O. Penas, A. Riviere, Multidisciplinary approach for modelling and optimization of Road Electric Vehicles in conceptual design level, in: IEEE Electrical Systems for Aircraft, Railway and Ship Propulsion (ESARS), 2012, pp. 1–6 [Google Scholar]
- A. Guizani, M. Hammadi, J.Y. Choley, T. Soriano, M.S. Abbes, M. Haddar, Electric vehicle design, modelling and optimization. Mech. Ind. 17, 405 (2016) [CrossRef] [EDP Sciences] [Google Scholar]
- G. Hamza, M. Hammadi, M. Barkallah, J.-Y. Choley, A. Riviere, J. Louati, M. Haddar, Conceptual design methodology for the preliminary study of a mechatronic system: application to wind turbine system, Mech. Ind. 18, 413 (2017) [Google Scholar]
- H. Siala, F. Mhenni, J.-Y. Choley, M. Barkallah, J. Louati, M. Haddar, General tolerance for mechatronic system, in: IEEE International Systems Engineering Symposium (ISSE), 2017, pp. 1–4 [Google Scholar]
- H. Siala, F. Mhenni, J.-Y. Choley, M. Barkallah, J. Louati, M. Haddar, Parametric tolerance specification of an electromechanical actuator, 12th France-Japan and 10th Europe-Asia Congress on Mechatronics, September 10–12, 2018 [Google Scholar]
- S.R. Buss, Introduction to inverse kinematics with jacobian transpose, pseudoinverse and damped least squares methods, IEEE J. Robot. Autom. 17, 16 (2004) [Google Scholar]
- M-S. Jha, G. Dauphin-Tanguy, B. Ould-Bouamama, Robust fault detection with interval valued uncertainties in bond graph framework, Control Eng. Pract. 71, 61–78 (2018) [Google Scholar]
- M. Ferber, A. Korniienko, J. Löfberg, F. Morel, G. Scorletti, C. Vollaire, Efficient worst‐case analysis of electronic networks in intervals of frequency. Int. J. Numer. Model. Electron. Netw. Dev. Fields, 31, e2249 (2018) [CrossRef] [Google Scholar]
- G. Zhai, Y. Zhou, X. Ye, B. Hu, A method of multi-objective reliability tolerance design for electronic circuits, Chin. J. Aeronaut. 26, 161–170 (2013) [CrossRef] [Google Scholar]
- E.K. Boukas, Systèmes asservis, Presses inter Polytechnique, 1995, Montreal, p. 323 [Google Scholar]
- H. Trabelsi, P.A. Yvars, J. Louati, M. Haddar, Evaluation of the effectiveness of the interval computation method to simulate the dynamic behavior of subdefinite system: application on an active suspension system. Int. J. Interact. Des. Manuf. 9, 83–96 (2015) [CrossRef] [Google Scholar]
- A.H. Abdessalem, N. Aifaoui, A. Benamara, et al., Tolerance analyses and optimizations methodology in integrated design: TOL-ANALYSES. Mech. Ind. 9, 381–395 (2008) [Google Scholar]
Cite this article as: H. Siala, F. Mhenni, M. Barkallah, J.-Y. Choley, J. Louati, M. Haddar, Variational approach for mechatronic tolerancing: application to a DC motor, Mechanics & Industry 21, 206 (2020)
All Tables
All Figures
 |
Fig. 1 Flowchart of the process of general tolerance for mechatronic system using variational approach. |
| In the text | |
 |
Fig. 2 DC motor model performed with Dymola (Modelica). |
| In the text | |
 |
Fig. 3 Variables curves. |
| In the text | |
 |
Fig. 4 Variables sensitivity to parameters variations. |
| In the text | |
 |
Fig. 5 Normal distribution and percentage of trust in a tolerance interval. |
| In the text | |
 |
Fig. 6 Variables variations in their tolerance intervals. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.


