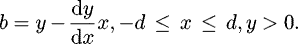| Issue |
Mechanics & Industry
Volume 22, 2021
|
|
|---|---|---|
| Article Number | 21 | |
| Number of page(s) | 13 | |
| DOI | https://doi.org/10.1051/meca/2021024 | |
| Published online | 01 April 2021 | |
Regular Article
Combination of oriented-plane curvature reproduction and squeeze film effect-based texture reproduction to simulate curved and textured surface
1
Department of Instrumental and Electrical Engineering, Xiamen University, Xiamen 361005, PR China
2
Fujian Branch of China United Network Communication Co., Ltd., Fuzhou 350001, PR China
3
Shenzhen Research Institute of Xiamen University, Shenzhen 518000, PR China
* e-mail: tao.zeng@xmu.edu.cn
Received:
14
October
2021
Accepted:
7
March
2021
The finger skin contains a variety of receptors, which provide multiple tactile sensing channels. When a finger touches the surface of an object, people can simultaneously perceive curvature, texture, softness, temperature, and so on. However, in most of research activities, the designed haptic feedback devices can only focus on a certain channel. In this paper, the rendering of curved and periodic textured surfaces involving two channels, i.e., curvature and texture, was studied. Two psychophysical experiments were conducted to investigate whether the coupling of kinesthetic feedback of curvature and tactile feedback of texture could reproduce curved and textured surfaces with high fidelity. The results showed a deviation of the point of subjective equality values in terms of curvature and roughness, indicating that the curvature rendering and texture rendering have an impact on each other. Therefore, it is necessary to correct the bias when making virtual rendering. The influence of curvature on texture rendering is reduced by recalculating and adjusting the spatial period of the synthesized texture in real-time; the influence of texture on curvature rendering is eliminate by compensating the force difference between touch on physical strip and artificial stimulus.
Key words: Kinesthetic platform / tactile display / curvature perception / texture perception
© T. Zeng et al., published by EDP Sciences 2021
 This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
This is an Open Access article distributed under the terms of the Creative Commons Attribution License (https://creativecommons.org/licenses/by/4.0), which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
1 Introduction
Curvature and texture are two haptic attributes of rigid objects, and these are correlated to the geometry of profile and the rugged surface, respectively. Three shape descriptors for object profiles are available to human sensing channels through touch, namely, height difference, attitude difference, and local curvature [1], which are also called position, slope (orientation), and local curvature [2]. They are termed zeroth-, first-, and second-order shape descriptors, respectively. Pont et al. [1] have proven the importance of first-order information in curvature rendering by using physical stimuli. Dostmohamed and Hayward [3] have designed a haptic device through controlling the orientation of a flat surface on which the fingertip was placed, and found that the first-order information can generate curvature perception through passive and dynamic touch. Wijntjes et al. [2] have reported that the discrimination thresholds have no significant differences between only the first-order information is available and both the zeroth- and first-order information are available. In summary, the first-order information dominates the curvature perception. Following the principle, a number of shape-rendering devices were proposed by controlling the orientation of a flat surface beneath the fingertip to respect the first-order information, i.e., the slope [4–11].
As for texture, it is well documented that the roughness is the dominant element in texture perception [12–16]. Studies on roughness have matured, that is, the physiological elements related with roughness perception are well understood. Researchers have studied the receptors, e.g., Pacinian, Meissner, Merkel, and Ruffini, that record mechanical stimuli in the skin and tactile responses of the cranial nerves to different object surfaces [17,18]. Accordingly, many tactile devices have emerged, such as the Scalable Latching display based on shape memory polymer membrane [19], the StimTac based on squeeze film effect [20], the TeslaTouch based on electrovibration [21], the Electrotactile display based on current stimulation [22], the Electroactive interface based on silver nanowire electrodes [23], the Touch-sensitive visual display based on polymer waveguides and microactuator array [24], and among others.
1.1 Previous work
In previous studies the curvature and texture were often considered as independent study subjects. Few studies have combined the two to simulate 3-dimensional shapes [5,7,25–29]. In such studies, however, the problem of mutual influence between them was not addressed. In [7], the proposed device consisted of two controllers, i.e., Normal Touch (for rendering object shape using a tiltable and extrudable platform) and Texture Touch (for rendering the texture through a 4 × 4 matrix of actuated pins). The two modules worked together to identify specific shapes. However, each module may have an impact on the other because of the complex cutaneous feedbacks at the fingerpads resulting from the richness of mechanoreceptors found in the fingerpads. In addition, as the finger is fixed in a thimble or aperture, touch becomes nonactive, which limits users' exploration into the curvature and texture. In [28,29], the authors tried to combine tactile and kinesthetic feedback to render texture and shape. However, these works were still in the initial stage, and the interaction between texture and shape is not addressed.
1.2 Aims of the study
The study serves two goals. One is to gain knowledge regarding haptic perception of curved and textured surface. By contrast, smooth curved surface and flat textured surface were well studied. We investigate originally whether the coupling of kinesthetic and tactile feedback could reproduce curved and textured surfaces with high fidelity. Here, the kinesthetic feedback of curvature and tactile feedback of texture employ mature technical solutions. For all that, we designed a kinesthetic platform with high accuracy, large rotation range and high curvature rendering ability to produce curved shape stimuli and a transparent texture-rendering plate with large work space to produce texture stimuli.
If, for a general application, the curvature rendering and texture rendering influence each other during the reproduction of curved and textured surface and result in a reproduction failure, then it leads to the second goal which is to find the methods that are available to render curved and textured surface haptically.
1.3 Approach
The study combined the oriented-plane curvature reproduction and the squeeze film effect-based texture reproduction to simulate curved and textured surfaces. The former makes the synthesized shape assume a flexible curvature with strong rigidity. In particular, the exploring behavior of user's finger is allowed to be active and dynamic [9,11], which is a necessary condition for texture reproduction based on squeeze film effect [20]. Consequently, this study proposes a kinesthetic platform to elevate, translate, and orient a texture-rendering plate which is based on squeeze film effect. The user can actively and dynamically explore the plate to simultaneously achieve curvature and roughness sensation with a large work space.
2 Proposed system and algorithm
2.1 Kinesthetic platform design
A kinesthetic platform to produce curved shape stimuli was designed, as presented in Figure 1. Two independently sliding lead screws and two servo motors decouple the x and y direction movements. The third servo motor drives the end-effector to rotate around the z axis, leading to large rotation range and reproducing the stimuli with desired curvature. The platform is closed loop system and a PID control is used. In accordance with the oriented-plane reproduction, this platform changes skin and muscle deformation at the fingertip by controlling the indentation depth between its flat end-effector and the fingerpad, with respect to the dominant cue for curvature perception, i.e., the first-order information, at the simulation of curved surfaces through passive and static touch [2], or the combination of zeroth- and first-order information at the simulation of curved surfaces through active and dynamic touch. Kinesthetic validation of this platform is proved in Figure 2 and experimental validation in the curvature perception is included in the following experiments (condition C in Experiment 1 and condition C' in Experiment 2). Because the translation and rotation velocities of the platform can't be infinitely fast and the fingerpad has a certain area, the platform can't simulate the geometry with complex surface curve or too fast curvature change or too high curvature.
 |
Fig. 1 Proposed system to produce curved and textured surface stimuli. A is the texture-rendering plate that has two functions: one is as texture display for texture rendering; the other is as oriented plate for curvature rendering. B1, B2, and B3 are servo motors (MSMD5AZG1U, Panasonic Inc.). C1, C2 and C3 are lead screws (SFSR1610, Chuanwei Inc.) and terminal connector. The servo motors and lead screws form the servo mechanisms to elevate, translate, and rotate the texture-rendering plate. D1, D2, and D3 are motor controllers (A5, Panasonic Inc.). E is piezoelectric actuator. |
 |
Fig. 2 Evaluation of the kinesthetic platform. (a) on x-axis horizontal motion; (b) on z-axis vertical motion; (c) on rotary motion around y-axis. |
2.2 Texture-rendering plate design
In consideration of the synchronous reproduction of texture and curvature, a texture-rendering plate was used as the end-effector (see Fig. 1, marked by A). The plate has a rigid and flat surface, which could display the fine texture based on film squeeze effect [20,30,31] and the curvature based on the oriented-plane curvature reproduction. The layout of this plate was shown at Figure 3a. The tactile display was attached to a 7-inch capacitive touchpad to measure the position of the finger in real time, and then paste them to a 7-inch visual screen of a consumer product to achieve visual and tactile sensation together.
The tactile display was designed based on squeeze film effect. This display was formed by a transparent and thin glass whose backside glued two lines of piezoelectric ceramics to excite the plate into bending resonance. Each piezoelectric ceramic has n resonance frequencies (fr ), and the resonance frequency of standing wave mode is the resonance frequency. The material properties of rectangular piezoelectric ceramics cut by laser are prone to change, thus an impedance analyzer was used to measure their impedance. Figure 3b presented the impedance diagram of one typical ceramic in which several resonance frequencies were more than 25 KHz (the least frequency for generating squeeze film effect [20]). The relation between frequency and half wave length is expressed in (6).
The piezoelectric ceramics were attached to both edges of the glass [32]. Modal analysis of glass plate plus piezoelectric ceramics was done, as depicted in Figure 3c. It shows that the resonance frequency of the device was 33.906 kHz and the half wavelength was 11.41 mm approximately. Evaluating the validation of this plate in the texture perception is also included in the following experiments (condition T in Experiment 1 and condition T' in Experiment 2).
This system can meet the requirement of making active and dynamic touch. The user is free to move his/her finger forward and backward along plate surface to simultaneously perceive the curvature and texture sensation on a large work space.
 |
Fig. 3 Design and characteristics of texture-rendering plate. (a) Layout of the plate. (b) Impedance diagram of typical piezoelectric ceramic. fr1, fr2, fr3, fr4, and fr5 are equal to 22.95, 25.31, 28.32, 32.06, and 34.71 KHz, respectively. The ceramic resonates at these frequencies as marked in red circles. (c) Modal analysis of glass plate and piezoelectric ceramics together to show standing wave. |
2.3 Algorithm
To respect the slope and slip cue in curvature rendering, the plate is oriented, translated and elevated to make the sliding trajectory coincide with the profile of the strip when the finger slide on the plate. Figure 4 illustrates the control method, where c is the curvature, r is the radius, d is the half length of the strip, (o,-h) is the center coordinate, (x, y) is the fingertip contact point, and b is the intersection of the plate and y axis. According to Pythagorean theorem, the circle and h can be expressed as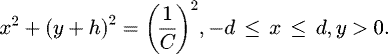 (1)
(1)
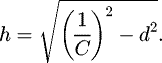 (2)
(2)
For a definite curvature, h is a fixed value.
In order to obtain the slope of the plate at (x, y) and the intersection point of b, the derivative of (1) is obtained by using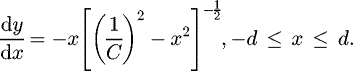 (3)
(3)
The point-slope form straight-line equation for the plate is given by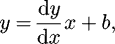 (4)
(4)
When x, y, slope, and b are obtained, the plate can be controlled to respect the first-order information and the slip cue (by zeroth-order information).
At texture rendering, the resonant frequency of the device can be estimated by the first natural frequency of a simply supported plate of the half wavelength (λ/2) [20] and is negatively correlated with the half wavelength which can be expressed by the following equation: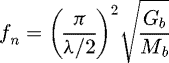 (6)
(6)
where fn is resonant frequency, Mb is the total surface mass, Gb is the bending rigidity. For making sure that the resonant frequency is greater than 25 kHz, the maximum value of the half wavelength is 20.87 mm.
In order to perceive and distinguish texture information, the vibration amplitude of the plate must be greater than 1 μm [20]. The vibration amplitude of the display is the dynamic deflection which is positively correlated with the half wavelength and can be expressed by the following equation [20]: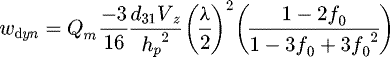 (7)where wdyn
is dynamic deflection, Qm
is mechanical quality factor which represents the energy consumption of piezoelectric ceramic due to overcoming internal friction during resonance, d31
is piezoelectric strain constant which characterizes the polarization (voltage) of a piezoelectric ceramic under pressure, Vz
is a supply voltage of piezoelectric ceramics, hp
is the thickness of piezoelectric ceramics, f0
is the ratio of the height of the neutral surface to the thickness of the piezoelectric ceramic. The mechanical properties of the plate are given in Table 1. For making sure that the dynamic deflection is greater than 1 μm for human perception, the minimum value of the half wavelength is 8.26 mm.
(7)where wdyn
is dynamic deflection, Qm
is mechanical quality factor which represents the energy consumption of piezoelectric ceramic due to overcoming internal friction during resonance, d31
is piezoelectric strain constant which characterizes the polarization (voltage) of a piezoelectric ceramic under pressure, Vz
is a supply voltage of piezoelectric ceramics, hp
is the thickness of piezoelectric ceramics, f0
is the ratio of the height of the neutral surface to the thickness of the piezoelectric ceramic. The mechanical properties of the plate are given in Table 1. For making sure that the dynamic deflection is greater than 1 μm for human perception, the minimum value of the half wavelength is 8.26 mm.
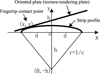 |
Fig. 4 Illustration of virtual shape and the control of oriented plate. c is the strip curvature, r is the radius, d is the half length of the strip, (o, −h) is the center coordinate, (x, y) is the fingertip contact point, and b is the intersection of the plate and y axis. |
Mechanical properties of the texture-rendering plate.
3 Evaluation
Two experiments were carried out to test the rendering effect. The discrimination thresholds and the perception biases in terms of curvature and roughness were measured.
3.1 Experiment 1
The purpose is to investigate (1) whether the designed kinesthetic platform could render curvature well; (2) whether the designed tactile plate could render texture well; (3) whether the combined system could render curvature well when texture rendering exists at the same time; (4) whether the combined system could render texture well when curvature rendering exists at the same time. The discrimination performances were examined by using a Just Noticeable Difference (JND) measurement [33]. In psychophysics, the JND (or “Difference Threshold”) is the minimum amount by which stimulus intensity must be changed in order to produce a noticeable variation in sensory experience. The smaller the JND is, the higher render sensitivity is achieved. Four stimuli conditions C, CT, T, and TC were applied and they were defined according to the used stimuli as presented in subsection b. Two scales of curvature were considered: the low curved and the high curved. For C and CT, we examined whether the added texture will change the difference threshold compared with curvature perception only. For T and TC, we examined whether the added curvature will change the difference threshold compared with pure texture perception.
3.1.1 Subjects
Ten volunteers (half males and half females) participated in this experiment. They were aged 20–28 and were undergraduate or graduate students. Using a modified version of the Edinburgh Handedness Inventory [34], we ensured that all the selected subjects use their dominant hand to explore the stimuli surface while performing the task. Baseline testing verified that they were sensitive to tactile cues. All of them were naïve to the purpose of the study.
3.1.2 Stimuli
The stimuli were all synthesized shapes or textures rendered by the proposed system as described in Table 2 and Figure 5. In condition C, the stimuli were the simulated truncated circular profiles that had constant curvatures. Two sets of curvatures were employed: one was 1.0 ± {0, 0.2, 0.4, 0.6, 0.8, 1.0} m−1 for the low curved stimuli (such as −2–2 m−1 in [2], −4–4 m−1 in [1], and 0–2 m−1 in [9]) and one was 20 ± {0, 0.8, 1.6, 2.4, 3.2, 4.0} m−1 for the high curved stimuli (such as 33.3 m−1 in median in [35], 33 m−1 in median in [36], and 10.61 m−1 in median in [11]). In condition CT, the stimuli were those in condition C mapped on a fixed texture pattern, which had a 4-mm spatial period. In condition T, the stimuli were textures with spatial period in 4 ± {0, 0.2, 0.4, 0.6, 0.8, 1.0} mm. In condition TC, the stimuli were those in condition T curved with 1 or 20 m−1 curvature. A total of seven kinds of stimuli were presented. They were the synthesized shapes with curvature only (low curved, under condition C), with curvature only (high curved, under condition C); with curvature plus texture (low curved, under condition CT), with curvature plus texture (high curved, under condition CT), with texture only (under condition T), with texture plus curvature (low curved, under condition TC), and with texture plus curvature (high curved, under condition TC)), respectively.
Description of conditions and stimuli in Exp. 1.
 |
Fig. 5 The stimuli. (a) A PVC strip with smooth surface. It is the prototype shape in Experiment 1 and one of the real reference stimuli in Experiment 2. (b) A PVC strip with textured surface. It is the prototype shape in Experiment 1. (c) A texture model (Gratings are single sided copper on printed circuit boards). It is the prototype shape in Experiment 1 and one of the real reference stimuli in Experiment 2. |
3.1.3 Procedure
To eliminate the effects of possibly uncontrolled cues, a block design was applied, wherein the orders of four conditions and seven kinds of stimuli were counterbalanced. Within each block, each test stimulus was randomly selected to form a pair with the reference stimulus. The order of test and reference stimuli and the order of the low curved stimuli and high curved stimuli were counterbalanced. The subjects were asked to perceive the stimuli and compare the curvature magnitudes and texture spatial periods. During the experiment, no feedback was given to the subjects. Before the experiment, we verified through a pilot testing that the subjects had a clear notion of what a high curvature magnitude and what a large texture spatial period meant.
The tasks were as follows. Firstly, each subject was asked to position his/her finger on the texture-rendering plate surface and to move the finger forward and backward once along the surface to perceive the curvature or the texture; secondly, the subject had to judge which of two stimuli was “more curved” or “more rough” by responding “the first one” or “the second one”. A two-alternative-forced-choice task was employed in which the subject was forced to make a choice even if he/she could not detect a difference. They were seated behind a curtain and wore a pair of headphones to prevent the visual and auditory interference.
The total comparison conducted by each subject was 840 (7 kinds of stimuli × 10 test stimuli × 12 repetitions). The experiment was performed in six sessions, each consisting of four blocks. Three blocks consisted of 40 trials each (two kinds of stimuli × 10 test stimuli × 2 repetitions). One block consisted of 20 trials (one kind of stimuli × 10 test stimuli × 2 repetitions). The sessions were separated by 20 min, and each subject spent about 3 h and half on average.
3.1.4 Results
To make comparisons under different dimensions and numerical ranges, the Weber fraction was computed based on JND measurements for the four conditions, as presented in Figure 6b. The Weber fraction can be measured graphically from a psychometric function [37]. The psychometric function is given by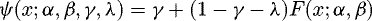 (8)where F (x ; α ; β) = 1− exp [− (x/α)
β
] , 0 ≤ x < ∞, x is the psychometric variable to be measured, F is Weibull function for fitting, and α and β are the fitting parameters. γ and λ were set to zero because the result scale was [0,1] and the lapse of subjects was heavily diminished. Figure 6a shows a representative example of data points and the psychometric function that was fitted to these data points. The JND for each reference shape was defined as the average of JNDL and JNDU.
(8)where F (x ; α ; β) = 1− exp [− (x/α)
β
] , 0 ≤ x < ∞, x is the psychometric variable to be measured, F is Weibull function for fitting, and α and β are the fitting parameters. γ and λ were set to zero because the result scale was [0,1] and the lapse of subjects was heavily diminished. Figure 6a shows a representative example of data points and the psychometric function that was fitted to these data points. The JND for each reference shape was defined as the average of JNDL and JNDU.
Under separate simulation, for the curvatures of the low and high curved stimuli (condition C), their discrimination thresholds are 46.8% (0.468 m−1) and 9.9%, respectively. These data are consistent with those reported in previous virtual curvature rendering studies, such as about 0.6 m−1 in [2], 0.45 m−1 in [9], and 6.8% in [11]. For the texture (condition T), its discrimination threshold is 9.5%, which is also consistent with that reported in the literature, such as 8.1% in [38]. Thus, the proposed device can separately distinguish the curvature or texture with high fidelity.
In order to evaluate the effect of presence of texture on curvature rendering, an analysis of variance (ANOVA) was performed in which the condition (C and CT) and stimuli type (low curved and high curved) were used as the factors. ANOVA is to remove the quotient of the mean square within the group (i.e. F value) with the mean square between the groups and compare it with 1. If F value is close to 1, it means that there is no statistically significant difference between the mean values of each group. If F value is far greater than 1, it means that there is statistically significant difference between the mean values of each group. P is the confidence interval of the calculated test statistic F. Only when the value of the given critical value is less than P (generally 0.05), this decision is desirable. It showed that there was no significant difference between conditions C and CT (F 1, 36 = 0.813; p = 0.373), and there was a significant difference between low curved stimuli and high curved stimuli (F 1, 36 = 186.872; p < 0.001). A one-way repeated ANOVA was conducted to evaluate the effect of presence of curvature on texture rendering. It showed that there was a significant effect among conditions T, low curved TC and high curved TC (F 2, 27 = 3.379; p = 0.0489). Furthermore, Bonferroni correction t-test showed a significant difference between conditions T and high curved TC (t 9 = 2.958; p = 0.016 < 0.025) and no significant difference between conditions T and low curved TC (t 9 = 1.617; p = 0.140).
 |
Fig. 6 (a) An exemplary figure on an individual psychometric fit. (b) Results of Exp.1. Weber fractions for the discrimination threshold of tactile cues under four conditions, where the diamond sign denotes using low curved stimuli, the cube sign denotes using high curved stimuli, and the circle sign denotes using texture stimuli only. |
3.1.5 Discussion
The results (in terms of JND) indicate that (1) the platform can render curvature well under separate simulation; (2) the plate can render texture well under separate simulation; (3) the combined system could render curvature well with the presence of texture rendering; (4) the combined system could render texture well with the presence of low curvature rendering, but not in the presence of high curvature rendering.
3.2 Experiment 2
As no significant differences of discrimination thresholds between conditions C and CT was observed, it indicates that the roughness had no obvious effect on curvature rendering sensitivity. However, the results could not indicate whether the roughness had an effect on curvature rendering, i.e., the synthesized shapes were actually perceived as being curved or not as real one. Similarly, neither the similar discrimination thresholds between conditions T and TC using low curved stimuli nor the different discrimination thresholds between conditions T and TC using high curved stimuli could indicate whether curvature had an effect on texture rendering. Therefore, we performed Experiment 2 to compare synthesized stimuli with real ones to answer the questions. The point of subjective equality (PSE) [39] between the real and synthesized shapes/textures was measured by using the method of constant stimuli, in which a real strip/texture was used as the reference stimulus, and the synthesized shapes/textures were used as the test stimuli. The closer the PSE is to the reference value, the better the rendering effect.
This experiment employed only the high curved stimuli in terms of curvature, because the results of Experiment 1 showed that the effect of curvature on texture discrimination threshold using high curved stimuli was relatively more significant than that using low curved stimuli.
3.2.1 Subjects
A new group of ten naïve subjects was recruited (six males and four females aged 19–30), using the same criteria as that in Experiment 1.
3.2.2 Stimuli
Two real models were used as reference stimuli. One was a smooth strip with curvature C = 20 m−1 and length L = 80 mm (see Fig. 5a). The other was a textured surface model with spatial period SP = 4 mm (see Fig. 5c). The test stimuli were the synthesized shapes with curvature only, curvature plus texture, texture only, and texture plus curvature, corresponding to condition C', CT', T', and TC', respectively. In conditions C' and CT', the test curvatures were 20 ± {0, 0.8, 1.6, 2.4, 3.2, 4.0} m−1. In condition CT', all the synthesized shapes were textured with the constant spatial period SP = 4 mm. In conditions T' and TC', the test spatial periods were 4 ± {0, 0.2, 0.4, 0.6, 0.8, 1.0} mm. In condition TC', all the synthesized surfaces were curved with the constant curvature C = 20 m−1.
3.2.3 Procedure
The procedure was similar with that in Experiment 1. In each trial, a pair of stimuli, i.e., a reference strip and a synthesized curved shape, or a reference textured surface and a synthesized textured shape, was presented to the subject who had to decide which one felt like it had larger curvature or higher roughness. The investigation purposes for each pair of reference and test stimuli were listed in Table 3. The reference stimulus was positioned at a fixed distance near the platform. Four conditions were measured in blocks and counterbalanced within the subject group.
A comparison of 528 trials (4 conditions × 11 test stimuli × 12 repetitions) for each reference-test pair was conducted. The experiment was performed in six sessions, each session consisting of four blocks. A block consisted of 22 trials (1 condition × 11 test stimuli × 2 repetitions). The sessions were separated by 20 min, and the whole experiment time for each subject lasted about 3 h on average.
Investigation purposes for each pair of reference and test stimuli in Exp. 2.
3.2.4 Results
The PSE was obtained at the value at which the psychological function value was equal to 0.5. In the result analysis, the emphasis was placed on the perceptual bias µ, i.e., the difference between the reference value and the PSE. If a positive bias is achieved, it means that the simulated shape was felt more curved or rougher than the real one; if a negative bias is achieved, it's the opposite.
Figure 7 presents the individual perceptual biases under four conditions. Paired t-test showed a significant difference between the conditions C' and CT' (t 9 = 3.770; p = 0.0044) and between the conditions T' and TC' (t 9 = 2.469; p = 0.0356).
 |
Fig. 7 Results of Exp. 2. Individual perceptual biases. (a) under Conditions C' and CT'; (b) under Conditions T' and TC'. |
3.2.5 Discussion
Under condition C', the absolute biases are small (within 16.5% of the reference curvature). In addition, six subjects showed negative biases and four subjects showed positive bias, indicating that the subjects had not systematically judged a rendered shape to have lower or higher curvature than a real shape. Thus, the proposed platform can reproduce the curvature with high fidelity. In comparison, under condition CT', with texture rendering at the same time, almost all of the subjects (except for subject 4) showed negative biases, indicating that the subjects had systematically judged a rendered shape to have lower curvature than a real shape. The results demonstrated that the presence of texture led participants to underestimate curvature. Under conditions T' and TC', the results showed similar phenomenological rendering effects (six subjects showed negative biases and four subjects showed positive bias vs. all of the subjects showed negative biases). To sum up, (1) the platform can render curvature well under separate simulation; (2) the plate can render texture well under separate simulation; (3) the combined system could not render curvature well with the presence of texture rendering; (4) the combined system could not render texture well with the presence of curvature rendering.
4 Elimination of interplay between curvature and roughness perception
The results of Experiment 1 revealed that the curvature and texture had no significant influence on each other with regards the discrimination threshold (except for conditions T vs. TC using high curved stimuli), whereas the results of Experiment 2 indicated that the curvature and texture remarkably influences each other in terms of reproduction fidelity. The synthetic surface was not as curved or rough as the real one, thus failing to support the hypothesis, i.e., the coupling of kinesthetic and tactile feedback could reproduce curved and textured surfaces with high fidelity. Therefore, elimination of interplay between curvature and roughness perception is required in artificial rendering of curved and textured surface.
4.1 Correct the bias of texture rendering at the presence of curvature
As shown in Figure 8a, the contact area of fingertip is attributed to a line in the lateral direction of finger, even though a compression plane is created by pressing the fingertip down on the texture rendering plate when a finger slides on it. Thus, the finger can be represented by a vertical down arrow. The concrete realization is through the capacitive screen position detection. Because the finger movement is a dynamic touch, it ensures the continuity of position detection after the position is concentrated to a line, so as to ensure the relative accuracy of position detection when the finger pulp position is concentrated to a line [23,40–42]. When the finger's position is at a smooth area, the high-frequency vibration of the plate produces a squeeze film between the finger and the plate, which reduces the friction and gives the user a smooth feeling. When the finger's position is at the rough area, the plate stops vibrating, and the inherent friction of the surface makes the user feel rough. The senses of smoothness and roughness appear alternately, resulting in a grating texture reproduction, as shown in Figure 8b. When the plate is placed horizontally and remains stationary, the finger sliding distance on the smooth (or rough) area is consistent with the actual length of the smooth (or rough) area. Thus, the grating texture is reproduced well, as proved by Experiment 2 under condition T'.
When texture and curvature are reproduced synchronously, the plate rotates around the z-axis with respect to the zeroth and first-order information, making the finger's sliding path a curved one. The sliding distance on the smooth (or rough) area is no longer consistent with the actual length of a smooth (or rough) area. To render the texture at the presence of curvature with high fidelity, the interval lengths of smooth area and rough area of the texture presented on the plate is recalculated as follows.
The sliding distance of the half spatial period of the texture is calculated according to the finger sliding trajectory. We convert the Cartesian coordinate system into a polar coordinate system (ρ, θ) located at the center of the circle (0, −h), as shown in Figure 9a. The following equation is obtained: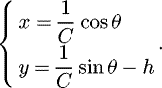 (9)
(9)
According to the above equation, the finger position x in the Cartesian coordinate system can be converted to θ in the polar coordinate system. (10)
(10)
The sector with arc length l
0 and radius 1/c is shown in Figure 9b. According to the relation between the arc length and angle, we can obtain.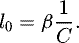 (11)
(11)
The formula of the angle corresponding to l
0 is given by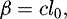 (12)
(12)
where β corresponds to the half spatial period of texture. Next, we set θ
0 as the angle between the edge of the sector and the horizontal direction. The angle corresponding to the boundary between rough and smooth can then be deduced as follows: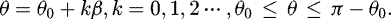 (13)
(13)
This improved texture reproduction algorithm was employed in synchronously rendering the texture and curvature.
Experiment 3 was conducted to evaluate the rendering scheme. Ten new volunteers were recruited for this evaluation. The experimental setting was similar to that in the condition TC' of Experiment 2. The results were collected in Figure 10. Under new algorithm, four individuals obtained positive bias and six individuals obtained negative bias. It showed that the subjects had not systematically judged a rendered texture to be rougher or smoother than a real one. Thus the results indicated that the new method could reproduce the curved grating texture with much higher fidelity than that used in the condition TC' of Experiment 2 (the results showed no positive bias). Furthermore, two sample t-test showed a significant difference between original algorithm and new algorithm (t18 = 1.805; p = 0.0439).
 |
Fig. 8 Illustration of (a) the concentration of fingertip on the texture rendering plate and (b) the generated grating texture feeling. |
 |
Fig. 9 (a) Virtual shape in the polar coordinate system. (b) One of the sectors whose arc length is the sliding distance corresponding to the half spatial period of the texture. (o,-h) is the center coordinate, (x, y) is the contact point, θ 0 is the angle between the edge of the sector and the horizontal direction, θ is the angle corresponding to the boundary between rough and smooth, r is the radius, C is the curvature, β is the half spatial period of texture, and l 0 is the arc length. |
 |
Fig. 10 Results of Exp. 3. Individual biases under new algorithm. |
4.2 Correct the bias of curvature rendering at the presence of texture
In general, slope (first-order information) plays a major role in curvature rendering, but some nongeometric factors, such as force, also plays a role. Robles-De-La-Torre and Hayward [43] found that a sense of bump or hole can be obtained when a propulsive or resisting force was applied to the fingerpad. Drewing and Ernst [44] verified that force cue has a higher weight than position cue in the simulation of small convex shallow arches. In fact, the forces reacted on finger when touches on physical strip at presence of texture is different from that when touches on tactile plate. Thus, we measured the two forces and developed a finger wearable device to compensate force difference.
The force diagram of the physical strip when the finger touches on is as shown in Figure 11a, b. F
N (strip) and f are the normal pressure and sliding friction of finger, respectively. F
N' (strip) and f ' are the reaction force on the strip, and mg is the gravity on the strip. The force sensor (@ATI Industrial Automation, Inc. NC 27539, USA; Specifications: Fx, Fy 300 N; Fz 380 N; Tx, Ty 3.2 Nm; Tz 4.6 Nm) is forced in the direction of Z-axis and X-axis, as shown in the lower right corner of Figure 11b, where the force represented by the red arrow is the resultant force of F
N' (strip) and f '. Then, the following equation holds.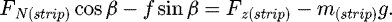 (14)
(14)
The sliding friction force f has the following relationship with F
N (strip), where µ is the sliding friction coefficient.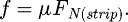 (15)
(15)
By combining the above two formulas, F
N (strip) is obtained: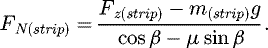 (16)
(16)
where, the angle β is determined by the finger position on the strip.
The force diagram of the tactile plate when the finger touches on is as shown in Figure 11c, d. The plate rotates at the angular velocity of ω. At this time, the force sensor is stressed in the Z-axis direction. Since the force sensor is also rotating, the resultant force is a centripetal force F
a
, as shown on the right side of Figure 11d. Then, the following equation holds.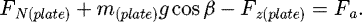 (17)
(17)
The centripetal force F
a
satisfies the following constraint: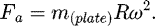 (18)
(18)
By combining the above two formulas, F
N (plate) is obtained: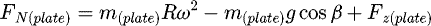 (19)
(19)
Then, the force different ΔF
N
is obtained: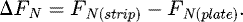 (20)
(20)
A finger wearable device was developed to compensate the force different by lifting or pressing the finger down, as shown in Figure 12. It used a piezoelectric linear motor as the actuator and featured light weight and good transparency.
Experiment 4 was conducted to evaluate the force compensation. Ten new volunteers were recruited. The experimental setting was similar to that in the condition CT' of Experiment 2, except with the finger wearable device. The results were collected in Figure 13. With force compensation, six individuals obtained positive bias and four individuals obtained negative bias. It showed that the subjects had not systematically judged a rendered strip to have higher or lower curvature than a real one. Two sample t-test showed a significant difference between original algorithm and new algorithm (t18 = −3.072; p = 0.0036). Thus the results indicated that the new method could reproduce the curvature at the presence of grating texture with much higher fidelity than that used in the condition CT' of Experiment 2 (the results showed only one positive bias).
 |
Fig. 11 Force measurement. (a) on physical strip; (b) illustration of the force on strip; (c) on tactile display; (d) illustration of the force on tactile display. |
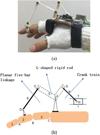 |
Fig. 12 The finger wearable device. (a) Outside view; (b) Schematic of the mechanical design. 1–7 are seven moving links: 1 is the distal phalange, 2 is the intermediate phalange, 3 is the proximal phalange, 4 is a linkage, 5 is the L-shaped rigid rod, 6 is a linkage, 7 is the sliding block; A to I are nine pairing elements: A, B, and C are finger joints, D, E, F, G, and H are revolute pairs, I is the guide rail. |
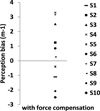 |
Fig. 13 Results of Exp. 4. Individual biases under the condition with force compensation. |
5 General discussion
The oriented-plane curvature reproduction and squeeze film effect-based texture reproduction were combined to simulate curved and textured surfaces. This method allows the finger to slide on the surface actively and dynamically with large work space. It is self-controlled touch with dynamic exploratory finger movement leading to better performance than other manners of touch. Such as in [5] and [25], the fingers were confined to a small space and can only make passive touch; in [7], the finger was fixed on a small surface and can only make static touch; in [26], the fingers needed to hold the end-effector and cannot move freely; in [27], a row of pins can only render small curvature. Results of Experiment 1 showed that the discrimination thresholds for smooth curved surfaces and flat textured surfaces were consistent with those reported in previous studies [2,9,11,38], providing the validation of proposed device. Furthermore, the results indicated that the presence of texture didn't influence the discrimination performance in terms of curvature, and the presence of low curvature didn't influence the discrimination performance in terms of texture (high curvature did). We can conclude that the coupling of kinesthetic feedback of curvature and tactile feedback of texture can almost simulate curved and textured surfaces from the perspective of discrimination performance. However, the results of Experiment 2 showed large perception biases in terms of curvature with synchronously rendering of texture and in terms of texture with synchronously rendering of curvature. Thus, the synthesized curved and textured shapes were not perceived as being curved or rough as real ones.
Therefore, it is necessary to correct the bias when making virtual rendering of curved and textured surface. This study solved the perception bias problem in texture rendering at the presence of curvature by recalculating the interval lengths of smooth and rough area of the grating, and in curvature rendering at the presence of texture by compensating the force difference between touch on physical strip and artificial stimulus.
6 Conclusion
At present, the research activities mainly focus on the tactile rendering of flat textured surface, while the research on rendering of curved and textured texture is rare. This paper studies the tactile rendering of curved and textured surface, which provides important theoretical basis and practical experience for the tactile representation of surface information in the field of consumer electronics, such as virtual simulation of the surface tactility of cultural relics, the simultaneous perception of object shape and texture in online shopping.
Acknowledgments
This research was funded by the Guiding Project of Industrial Technology Development and Application (Fujian Science and Technology Project), grant number 2019H0004, the National Nature Science Foundations of China, grant number 61403320, and the Knowledge Innovation Program of Shenzhen City (Fundamental Research, Free Exploration), grant number JCYJ20170306141926192.
References
- S.C. Pont, A.M.L. Kappers, J.J. Koenderink, Similar mechanisms underlie curvature comparison by static and by dynamic touch, Percept. Psychophys. 61, 874–894 (1999) [PubMed] [Google Scholar]
- M.W.A. Wijntjes, A. Sato, V. Hayward, A.M.L. Kappers, Local surface orientation dominates haptic curvature discrimination, IEEE Trans. Haptics 2, 94–102 (2009) [PubMed] [Google Scholar]
- H. Dostmohamed, V. Hayward, Trajectory of contact region on the fingerpad gives the illusion of haptic shape, Exp. Brain Res. 164, 387–394 (2005) [Google Scholar]
- G. Cini, A. Frisoli, S. Marcheschi, F. Salsedo, M. Bergamasco, A novel fingertip haptic device for display of local contact geometry, in: First Joint Eurohaptics Conf. and Symp. Haptic Interfaces for Virtual Environment and Teleoperator Systems (WHC '05), 2005, pp. 602–605 [Google Scholar]
- M. Gabardi, M. Solazzi, D. Leonardis, A. Frisoli, A new wearable fingertip haptic interface for the rendering of virtual shapes and surface features, in: IEEE Haptics Symp. 2016, pp. 140–146 [Google Scholar]
- M. Memeo, L. Brayda, Mind the bump: effect of geometrical descriptors on the perception of curved surfaces with a novel tactile mouse, Haptics: Perception, Devices, Control, and Applications, PT II: Lecture Notes in Computer Science 9775, 438–448 (2016) [Google Scholar]
- H. Benko, C. Holz, M. Sinclair, E. Ofek, Normal Touch and Texture Touch: High-fidelity 3D haptic shape rendering on handheld virtual reality controllers, in: Annu. ACM Symp. User Interface Software & Technology, 2016, pp. 717–728 [Google Scholar]
- A.G. Perez, D. Lobo, F. Chinello, G. Cirio, M. Malvezzi, J.S. Martin, D. Prattichizzo, M.A. Otaduy, Optimization-based wearable tactile rendering, IEEE Trans. Haptics 10, 254–264 (2017) [PubMed] [Google Scholar]
- S.C. Kim, B.K. Han, D.S. Kwon, Haptic rendering of 3D geometry on 2D touch surface based on mechanical rotation, IEEE Trans. Haptics 11, 140–145 (2018) [PubMed] [Google Scholar]
- M. Solazzi, A. Frisoli, M. Bergamasco, Design of a cutaneous fingertip display for improving haptic exploration of virtual objects, in: 19th International Symposium in Robot and Human Interactive Communication, 2010, pp. 1–6 [Google Scholar]
- T. Zeng, F. Giraud, B. Lemaire-Semail, M. Amberg, Contribution of slip cue to curvature perception through active and dynamic touch, IEEE Trans. Haptics 6, 408–416 (2013) [PubMed] [Google Scholar]
- W.M.B. Tiest, A.M.L. Kappers, Analysis of haptic perception of materials by multidimensional scaling and physical measurements of roughness and compressibility, Acta Psychol. 121, 1–20 (2006) [Google Scholar]
- M.D. Bartolomeo, F. Morelli1, D. Tonazzi, F. Massi, Y. Berthier, Investigation of the role of contact-induced vibrations in tactile discrimination of textures, Mech. Ind. 18, 404 (2017) [Google Scholar]
- D. Picard, C. Dacremont, D. Valentin, A. Giboreau, Perceptual dimensions of tactile textures, Acta Psychol. 114, 165–184 (2003) [Google Scholar]
- C. Tymms, D. Zorin, E.P. Gardner, Tactile perception of the roughness of 3-D-printed textures, J. Neurophysiol. 119, 862–876 (2018) [Google Scholar]
- W. Hassan, A. Abdulali, S. Jeon, Authoring new haptic textures based on interpolation of real textures in affective space, IEEE Trans. Ind. Electron. 67, 667–676 (2020) [Google Scholar]
- K.O. Johnson, The roles and functions of cutaneous mechanoreceptors, Curr. Opin. Neurobiol. 11, 455–461 (2001) [CrossRef] [PubMed] [Google Scholar]
- K.O. Johnson, T. Yoshioka, F. Vega-Bermudez, Tactile functions of mechanoreceptive afferents innervating the hand, J. Clin. Neurophysiol. 17, 539–558 (2000) [Google Scholar]
- N. Besse, S. Rosset, J.J. Zarate, E. Ferrari, L. Brayda, H. Shea, Understanding graphics on a scalable latching assistive haptic display using a shape memory polymer membrane, IEEE Trans. Haptics 11, 30–38 (2018) [PubMed] [Google Scholar]
- M. Biet, F. Giraud, B. Lemaire-Semail, Squeeze film effect for the design of an ultrasonic tactile plate, IEEE Trans. Ultrasonics, Ferroelectrics and Frequency Control 54, 2678–2688 (2007) [Google Scholar]
- I. Poupyrev, O. Bau, A. Israr, C. Harrison, Electrovibration for touch surfaces, United States Patent, no. US 9501145B2, 2016. [Google Scholar]
- M.E. Altinsoy, S. Merchel, Electrotactile feedback for handheld devices with touch screen and simulation of roughness, IEEE Trans. Haptics 5, 6–13 (2012) [PubMed] [Google Scholar]
- K. Jun, J. Kim, Il-K. Oh, An electroactive and transparent haptic interface utilizing soft elastomer actuators with silver nanowire electrodes.Small (Weinheim an der Bergstrasse, Germany), pp. e1801603, 2018 [Google Scholar]
- S. Park, S. Park, B. Park, S. Ryu, S.M. Jeong, K. Kyung, A soft and transparent visuo-haptic interface pursuing wearable Devices, IEEE Trans. Ind. Electron. 67, 717–724 (2020) [Google Scholar]
- C. Pacchierotti, D. Prattichizzo, K.J. Kuchenbecker, Cutaneous feedback of fingertip deformation and vibration for palpation in robotic surgery, IEEE Trans. Biomed. Eng. 63, 278–287 (2016) [Google Scholar]
- Z. Kang, K. Kim, Multimodal perception study on virtual 3-D curved textures with vision and touch for interactive multimedia systems, Multimed. Tools Appl. 77, 2209–2223 (2018) [Google Scholar]
- K. Zhang, E.J. Gonzalez, J. Guo, S. Follmer, Design and analysis of high-resolution electrostatic adhesive brakes towards static refreshable 2.5D tactile shape display, IEEE Trans. Haptics (2020). DOI: 10.1109/TOH.2019.2940219 [Google Scholar]
- T. Zeng, F. Giraud, B. Lemaire-Semail, M. Amberg, Analysis of a new haptic display coupling tactile and kinesthetic feedback to render texture and shape, in: Haptics: Generating and Perceiving Tangible Sensations. EuroHaptics 2010. Lecture Notes in Computer Science, vol. 6192, 2010, pp. 87–93 [Google Scholar]
- T. Zeng, Conception et contrôle d'un périphérique dédié à la simulation couplée kinesthésique et tactile, PhD thesis, University of Lille 1, France, 2012 [Google Scholar]
- M. Wiesendanger, Squeeze film air bearings using piezoelectric bending elements, Ecole Polytechnique Fdrale de Lausanne, Lausanne: EPFL, 2001 [Google Scholar]
- L. Winfield, J. Glassmire, J.E. Colgate, M.A. Peshkin (editors), T-pad: Tactile pattern display through variable friction reduction. in: 2nd Joint EuroHaptics Conference and Symposium on Haptic Interfaces for Virtual Environments and Teleoperator Systems, 2007, pp. 421–426 [Google Scholar]
- E. Vezzoli, T. Sednaoui, M. Amberg, F. Giraud, B. Lemaire-Semail, Texture rendering strategies with a high fidelity − capacitive visual-haptic friction control device. in: International Conference on Human Haptic Sensing and Touch Enabled Computer Applications, 2016, pp. 251–260 [Google Scholar]
- G. Gescheider, Psychophysics: the fundamentals, 3rd edn. Lawrence Erlbaum Associates, 1997 [Google Scholar]
- R.C. Oldfield, The assessment and analysis of handedness: the Edinburgh inventory, Neuropsychologia 9, 97–113 (1971) [CrossRef] [PubMed] [Google Scholar]
- I. Gordon, V. Morison, The haptic perception of curvature, Perception and Psychophysics 31, 446–450 (1982) [Google Scholar]
- B.J. Van der Horst, A.M.L. Kappers, Haptic curvature comparison of convex and concave shapes, Perception 37, 1137–1151 (2008) [PubMed] [Google Scholar]
- D.M. Green, J.A. Swets, Signal Detection Theory and Psycho-physics, 3rd edn. Peninsula Pub., 1988 [Google Scholar]
- M. Biet, Conception et controle d'actionneurs electro-actifs dedies a la stimulation tactile, PhD dissertation, Laboratory of Electrical Engineering and Power Electronics, University of Lille 1, France, 2008 [Google Scholar]
- R.H. Mcallister-Williams, D. Bertrand, H. Rollema, R.S. Hurs, L.R.M. Bevilaqua, Point of Subjective Equality. in: I.P. Stolerman (Eds.), Encyclopedia of Psychopharmacology, Springer, Berlin, Heidelberg, 2010 [Google Scholar]
- I. Poupyrev, S. Maruyama, Tactile interfaces for small touch screens. In: Symposium on User Interface Software and Technology, UIST 2003, pp. 217–220, 2003 [Google Scholar]
- Immersion. http://www.immersion.com [Google Scholar]
- T. Kaaresoja, L. Brown, J. Linjama, Snap-crackle-pop: tactile feedback for mobile touch screens. in: Eurohaptics 2006, 2006, pp. 565–566 [Google Scholar]
- G. Robles-De-La-Torre, V. Hayward, Force can overcome object geometry in the perception of shape through active touch, Nature 412, 445–448 (2001) [PubMed] [Google Scholar]
- K. Drewing, M.O. Ernst, Integration of force and position cues for shape perception through active touch, Brain Research 1078, 92–100 (2006) [PubMed] [Google Scholar]
Cite this article as: T. Zeng, Y. Liu, E. Ouyang, Combination of oriented-plane curvature reproduction and squeeze film effect-based texture reproduction to simulate curved and textured surface, Mechanics & Industry 22, 21 (2021)
All Tables
All Figures
 |
Fig. 1 Proposed system to produce curved and textured surface stimuli. A is the texture-rendering plate that has two functions: one is as texture display for texture rendering; the other is as oriented plate for curvature rendering. B1, B2, and B3 are servo motors (MSMD5AZG1U, Panasonic Inc.). C1, C2 and C3 are lead screws (SFSR1610, Chuanwei Inc.) and terminal connector. The servo motors and lead screws form the servo mechanisms to elevate, translate, and rotate the texture-rendering plate. D1, D2, and D3 are motor controllers (A5, Panasonic Inc.). E is piezoelectric actuator. |
| In the text | |
 |
Fig. 2 Evaluation of the kinesthetic platform. (a) on x-axis horizontal motion; (b) on z-axis vertical motion; (c) on rotary motion around y-axis. |
| In the text | |
 |
Fig. 3 Design and characteristics of texture-rendering plate. (a) Layout of the plate. (b) Impedance diagram of typical piezoelectric ceramic. fr1, fr2, fr3, fr4, and fr5 are equal to 22.95, 25.31, 28.32, 32.06, and 34.71 KHz, respectively. The ceramic resonates at these frequencies as marked in red circles. (c) Modal analysis of glass plate and piezoelectric ceramics together to show standing wave. |
| In the text | |
 |
Fig. 4 Illustration of virtual shape and the control of oriented plate. c is the strip curvature, r is the radius, d is the half length of the strip, (o, −h) is the center coordinate, (x, y) is the fingertip contact point, and b is the intersection of the plate and y axis. |
| In the text | |
 |
Fig. 5 The stimuli. (a) A PVC strip with smooth surface. It is the prototype shape in Experiment 1 and one of the real reference stimuli in Experiment 2. (b) A PVC strip with textured surface. It is the prototype shape in Experiment 1. (c) A texture model (Gratings are single sided copper on printed circuit boards). It is the prototype shape in Experiment 1 and one of the real reference stimuli in Experiment 2. |
| In the text | |
 |
Fig. 6 (a) An exemplary figure on an individual psychometric fit. (b) Results of Exp.1. Weber fractions for the discrimination threshold of tactile cues under four conditions, where the diamond sign denotes using low curved stimuli, the cube sign denotes using high curved stimuli, and the circle sign denotes using texture stimuli only. |
| In the text | |
 |
Fig. 7 Results of Exp. 2. Individual perceptual biases. (a) under Conditions C' and CT'; (b) under Conditions T' and TC'. |
| In the text | |
 |
Fig. 8 Illustration of (a) the concentration of fingertip on the texture rendering plate and (b) the generated grating texture feeling. |
| In the text | |
 |
Fig. 9 (a) Virtual shape in the polar coordinate system. (b) One of the sectors whose arc length is the sliding distance corresponding to the half spatial period of the texture. (o,-h) is the center coordinate, (x, y) is the contact point, θ 0 is the angle between the edge of the sector and the horizontal direction, θ is the angle corresponding to the boundary between rough and smooth, r is the radius, C is the curvature, β is the half spatial period of texture, and l 0 is the arc length. |
| In the text | |
 |
Fig. 10 Results of Exp. 3. Individual biases under new algorithm. |
| In the text | |
 |
Fig. 11 Force measurement. (a) on physical strip; (b) illustration of the force on strip; (c) on tactile display; (d) illustration of the force on tactile display. |
| In the text | |
 |
Fig. 12 The finger wearable device. (a) Outside view; (b) Schematic of the mechanical design. 1–7 are seven moving links: 1 is the distal phalange, 2 is the intermediate phalange, 3 is the proximal phalange, 4 is a linkage, 5 is the L-shaped rigid rod, 6 is a linkage, 7 is the sliding block; A to I are nine pairing elements: A, B, and C are finger joints, D, E, F, G, and H are revolute pairs, I is the guide rail. |
| In the text | |
 |
Fig. 13 Results of Exp. 4. Individual biases under the condition with force compensation. |
| In the text | |
Current usage metrics show cumulative count of Article Views (full-text article views including HTML views, PDF and ePub downloads, according to the available data) and Abstracts Views on Vision4Press platform.
Data correspond to usage on the plateform after 2015. The current usage metrics is available 48-96 hours after online publication and is updated daily on week days.
Initial download of the metrics may take a while.